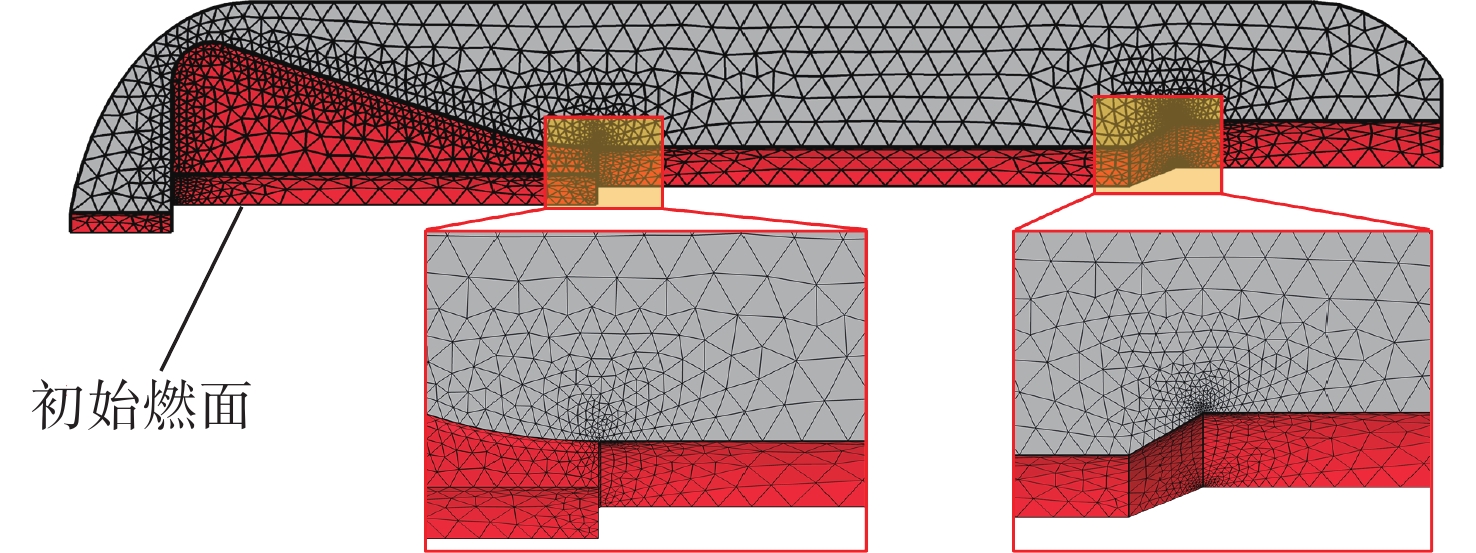
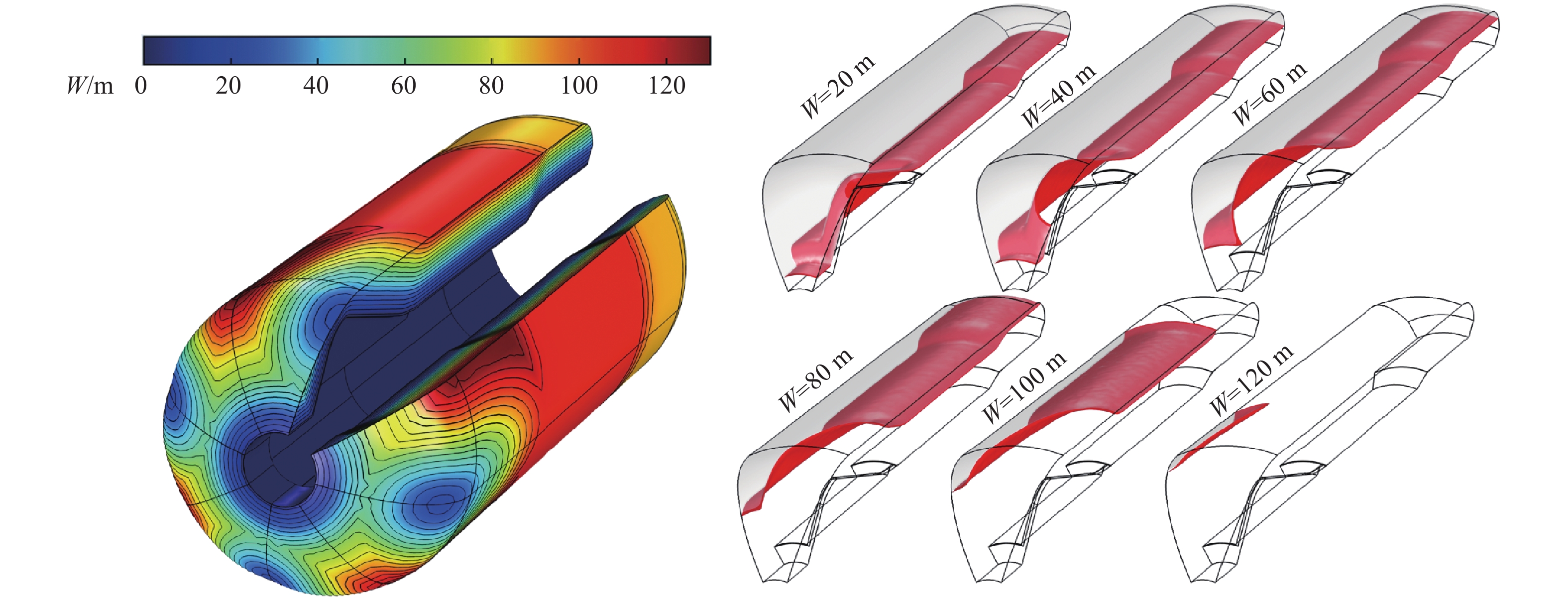
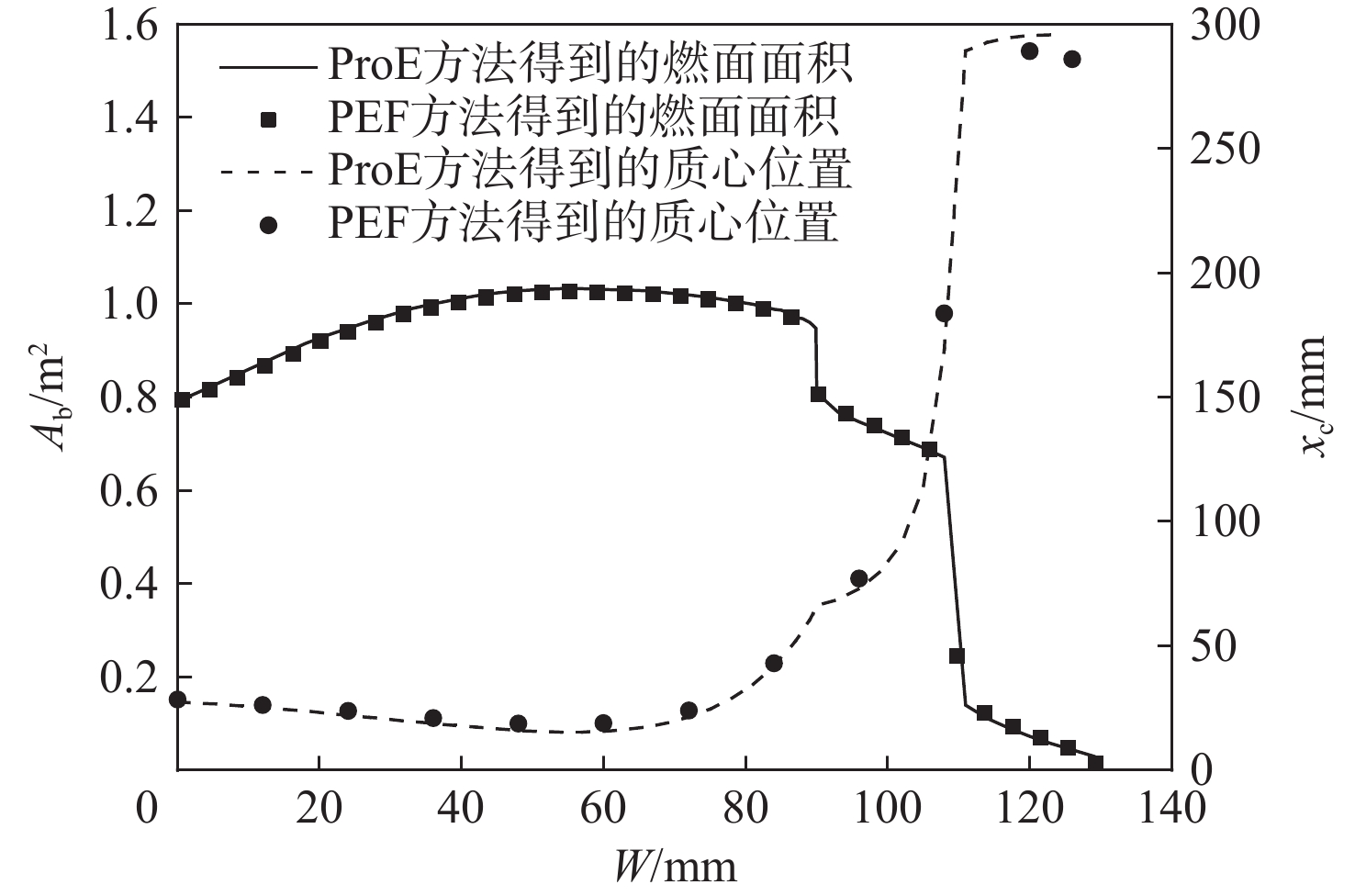
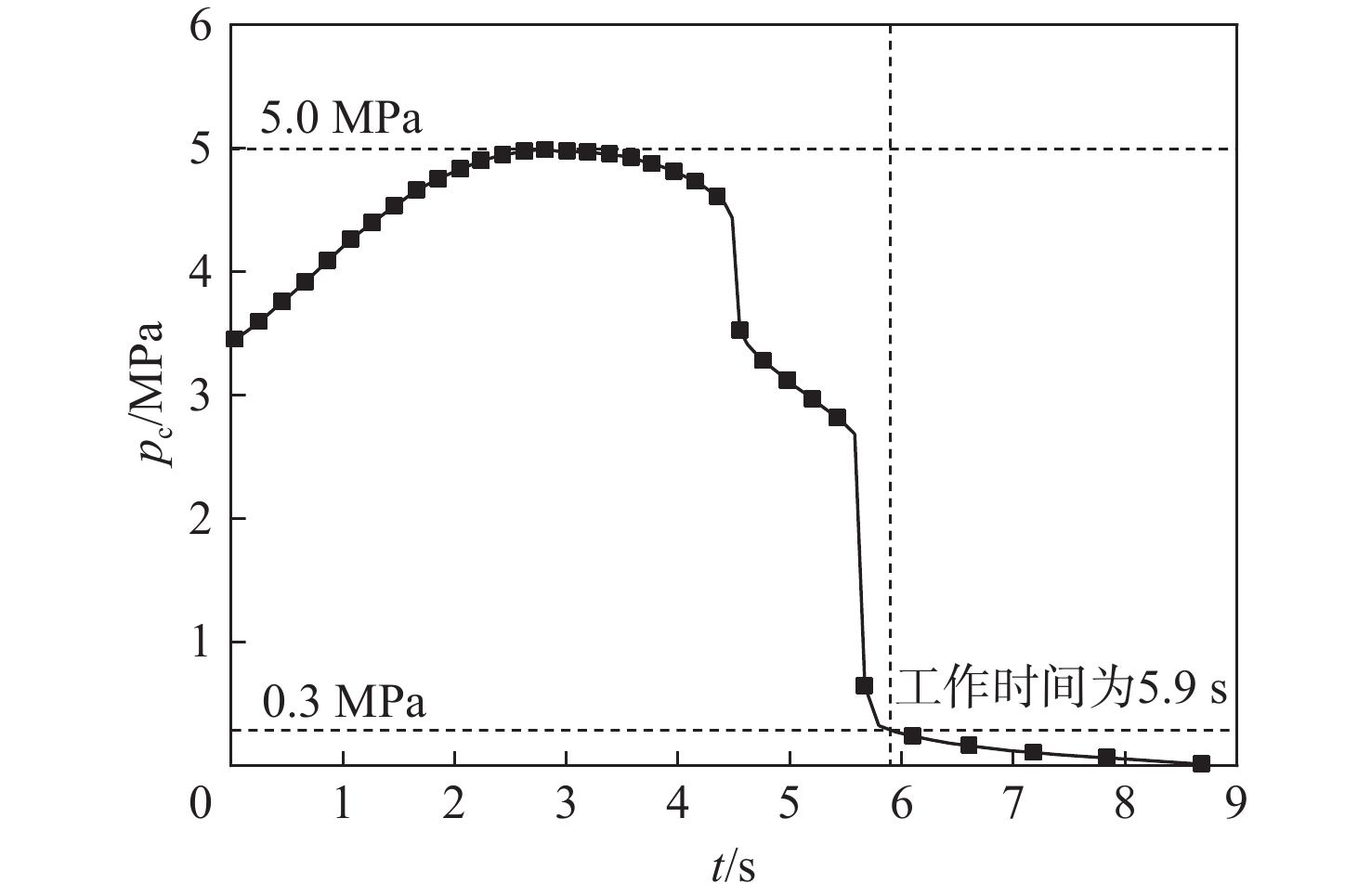
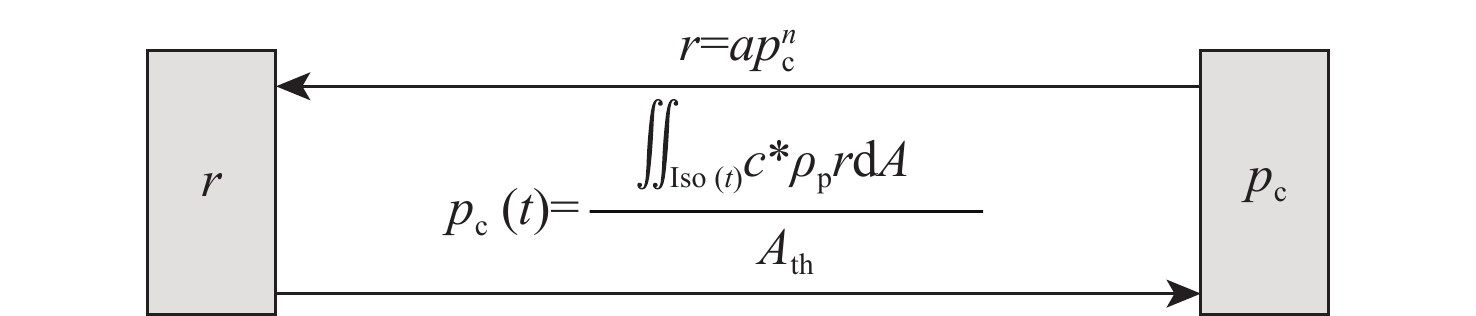Complex burn-back analysis and internal ballistic performance prediction of non-uniform grain
-
摘要:
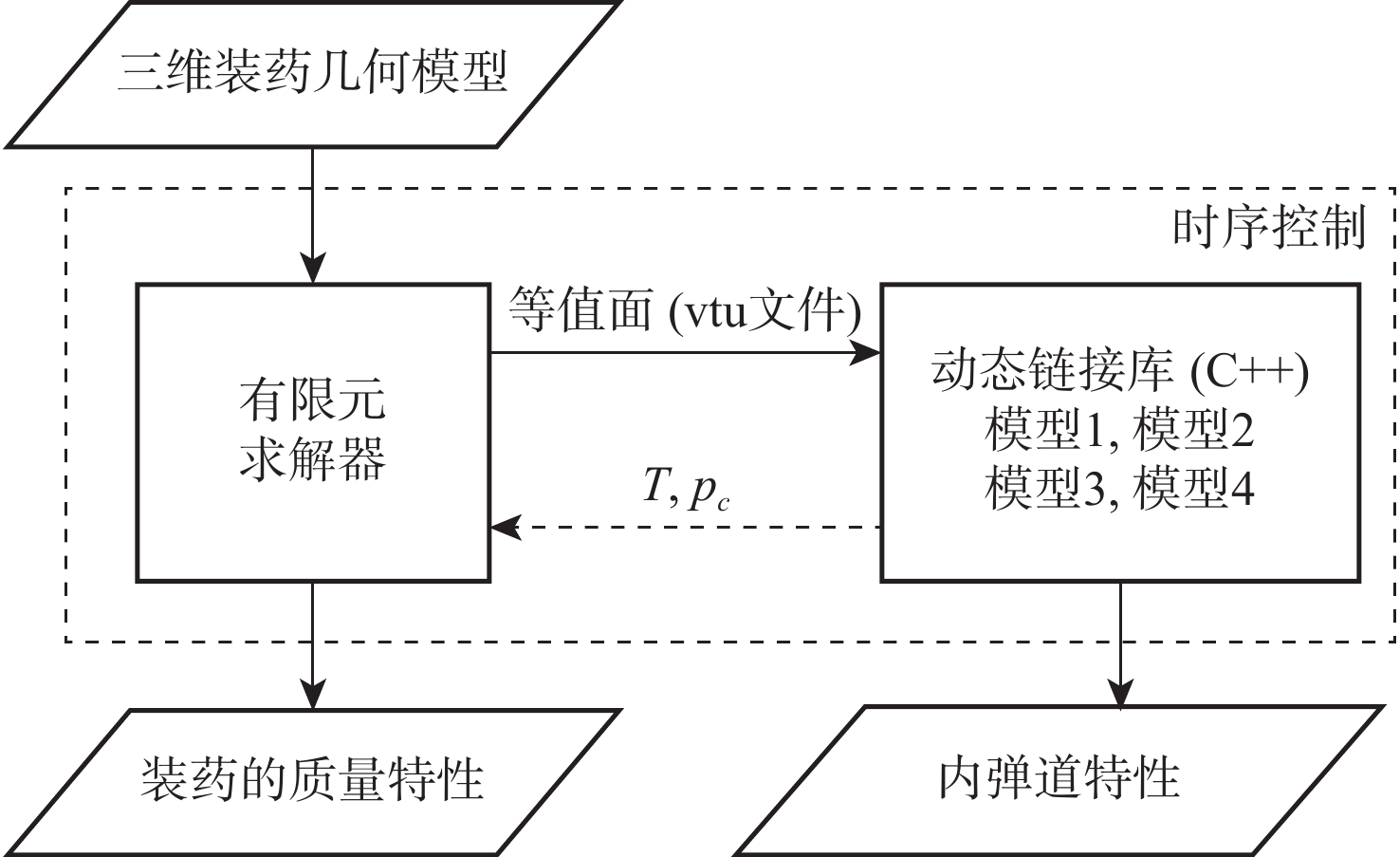
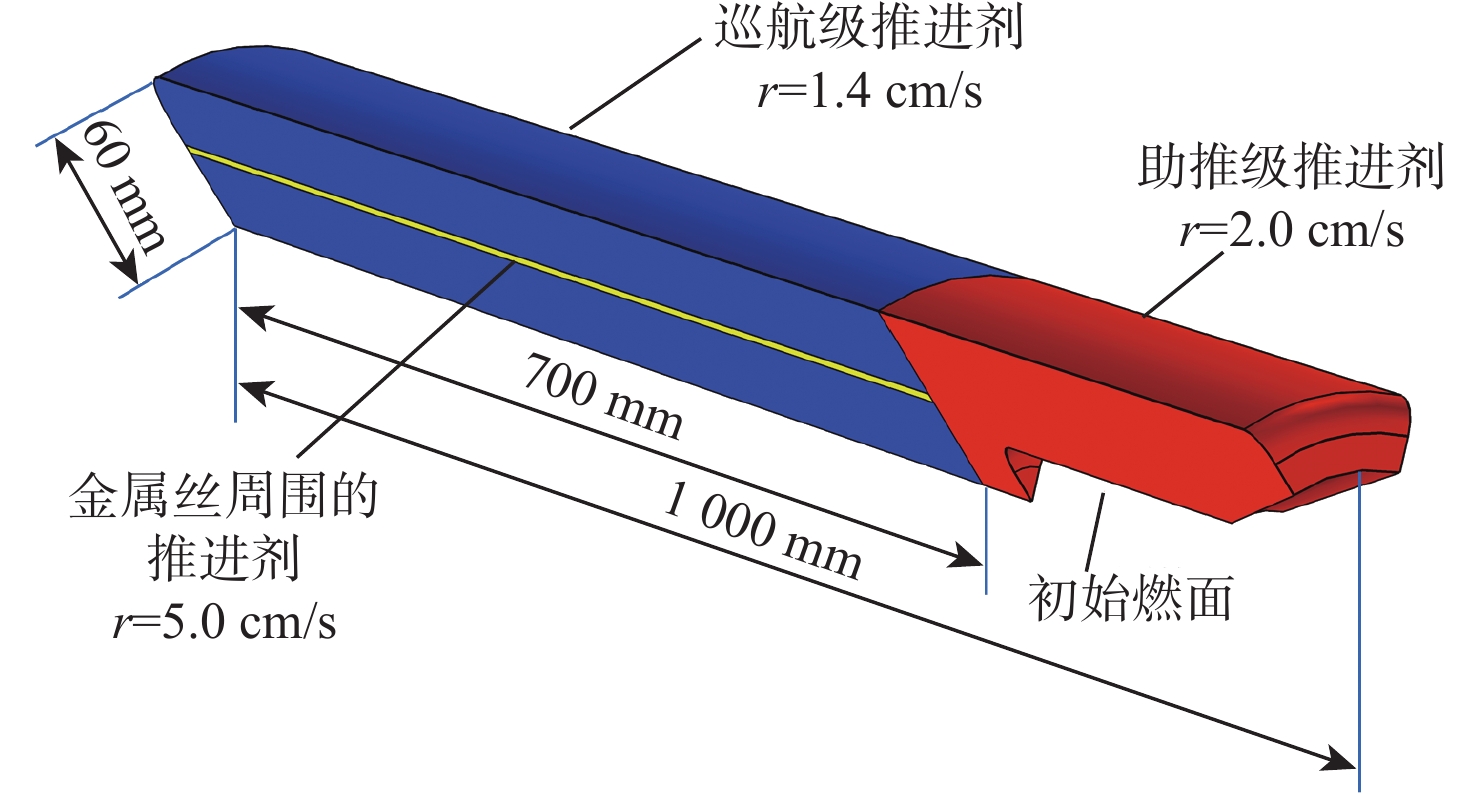
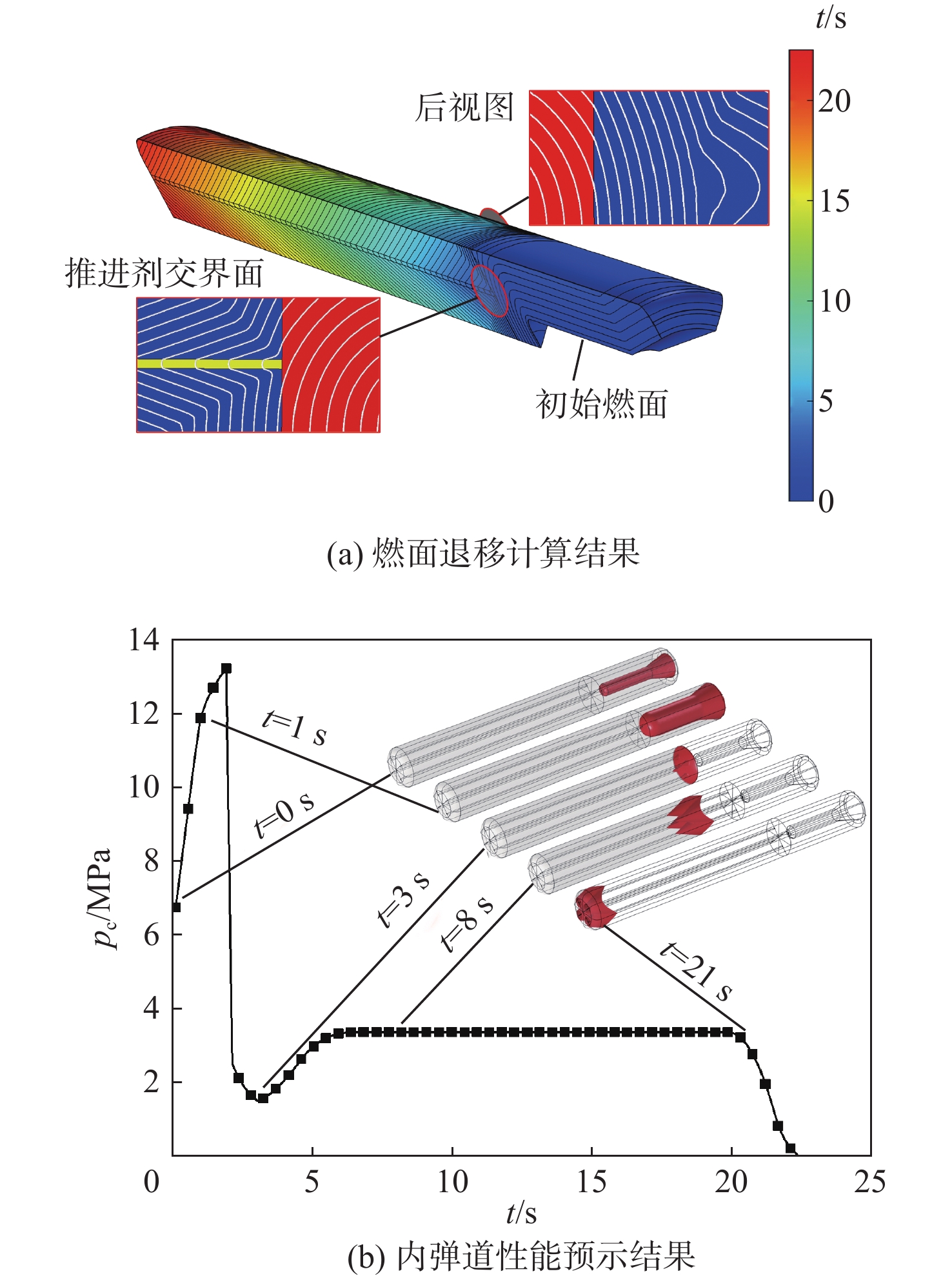
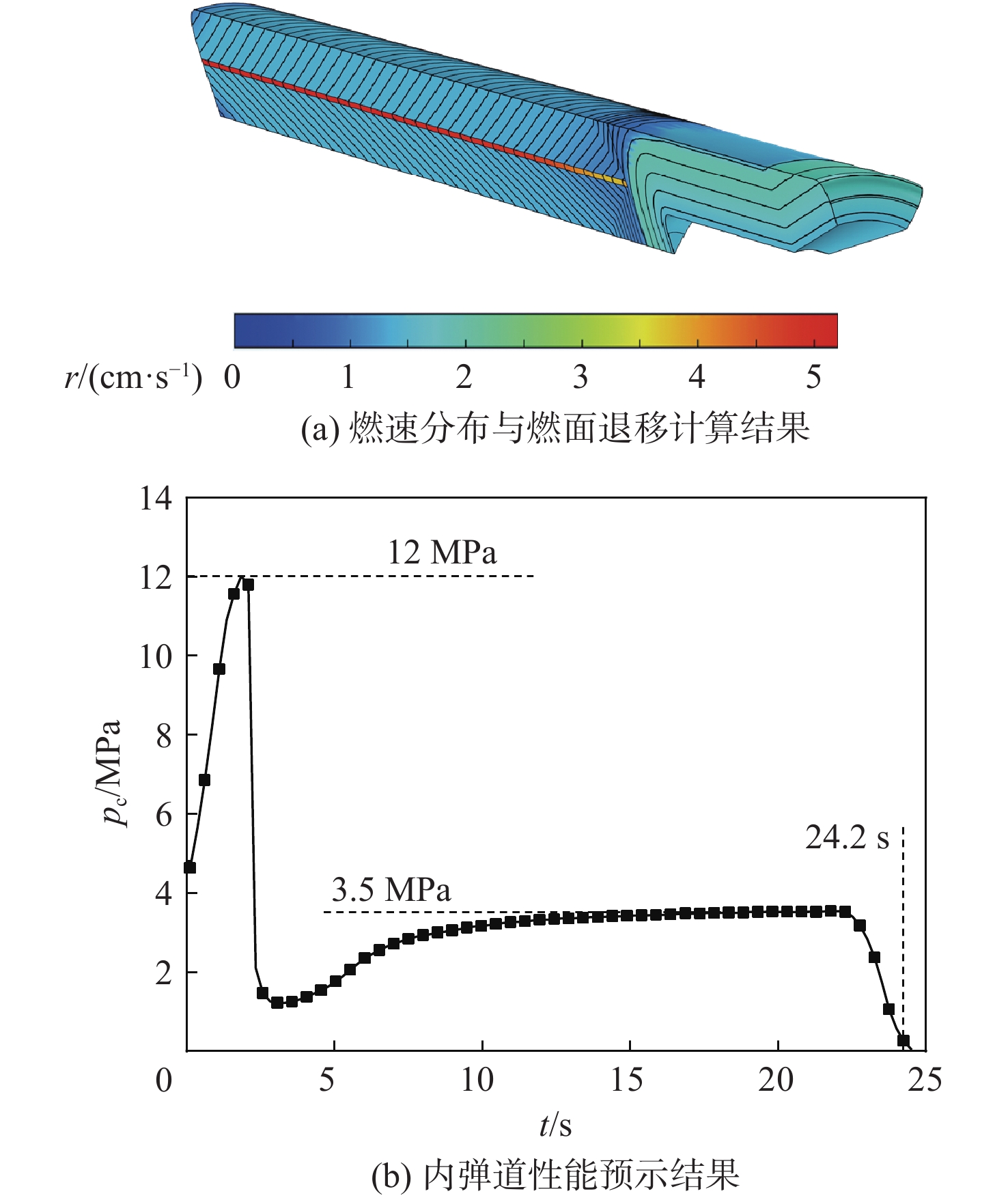
非均匀装药的复杂燃面退移与内弹道性能预示是固体火箭发动机设计的核心问题。建立非均匀装药燃烧的燃面退移数学模型，提出一种采用有限元法通过求解泊松方程逼近程函方程黏滞解的新方法（PEF）。所提方法可将燃面退移问题转化为特殊的稳态热传导问题，实现对几何形状不规则且燃速分布复杂的三维装药燃面退移的计算。考虑燃烧室压力变化等实际因素，在平衡压力假设下，形成了内弹道性能预示的4种计算模型。完成了二维星型装药、三维翼柱型装药和含金属丝的双推进剂装药的计算。计算结果表明：所提方法不仅可以高精度地适应多种推进剂构成的复杂交界面，而且可以直接在商业有限元软件的稳态热传导模块上应用和求解，充分利用商业有限元软件成熟的计算机辅助设计(CAD)建模、前处理、后处理及二次开发能力，实现了复杂燃面退移与内弹道性能预示方法的通用化和实用化。
Abstract:The complex burn-back analysis and internal ballistic performance prediction of the non-uniform grain are the core issues in solid rocket motor design. A mathematical model of burn-back analysis of combustion with non-uniform grain was established. A new method, namely Poisson equation-eikonal equation-finite element method (PEF) was proposed to approach the viscous solution of the eikonal equation by solving a Poisson equation using the finite element method. The proposed method can transform the burn-back problem into a special stationary thermal conduction problem and realize the burn-back calculation of the 3D grain with irregular geometry and complicated burning rate distribution. Then, the actual factors such as the change in combustion chamber pressure were considered, and four calculation models for internal ballistic performance prediction were developed under the assumption of equilibrium pressure. The calculation of 2D star grain, 3D finocyl grain, and dual propellant grain with metal wires embedded was completed. The calculation results show that the proposed method can precisely adapt to the complex interfaces of different propellants. The proposed method can be directly applied and solved in the stationary thermal conduction module of the commercial finite element software. It can fully utilize the mature capabilities of computer-aided design (CAD) modeling, pre-processing, post-processing, and secondary development in commercial finite element software, achieving universality and practicality of the complex burn-back analysis and internal ballistic performance prediction method.
-
图 3 一维烧去肉厚场控制方程的Jacobi矩阵条件数
Figure 3. Condition number of Jacobi matrix of control equation for 1D burned web thickness field
图 5 内弹道性能预示的4种模型的流程
Figure 5. Flow diagram of four models for internal ballistic performance prediction
图 6 燃速与燃烧室压力之间的耦合关系
Figure 6. Coupling relationship between burning rate and combustion chamber pressure
图 7 基于有限元软件的内弹道性能预示系统框架
Figure 7. System framework of internal ballistic performance prediction based on finite element software
图 9 不同$\alpha $值对应的星型装药燃面退移结果
Figure 9. Burn-back result of star grain with different $\alpha $values
图 10 半个星角的燃烧边长的计算结果
Figure 10. Calculation result of burned side length of a half star angle
图 12 不同$\alpha $值下星型装药的内弹道性能预示结果
Figure 12. Internal ballistic performance prediction result of star grain for different $\alpha $ values
图 16 燃面面积与质心位置随肉厚的变化
Figure 16. Variation of burned area and centroid position with web thickness
图 17 翼柱型装药的内弹道性能预示结果
Figure 17. Internal ballistic performance prediction result of finocyl grain
图 18 含金属丝双推进剂装药的几何形状
Figure 18. Geometry of dual-propellant grain with metal wires embedded
图 20 双平台推进剂装药的计算结果
Figure 20. Calculation result of dual propellant grain with platform
图 21 非平台双推进剂装药的计算结果
Figure 21. Calculation result of dual-propellant grain without platform
表 1 星型装药的参数
Table 1. Parameters of star grain
${R_{\text{o}}}$/m ${R_{\text{p}}}$/m $f$/m $\varepsilon' $ $\theta $/(°) $N' $ 1.0 0.5 0.03 0.8 80 6 
下载: 导出CSV
表 2 双推力装药的网格无关性验证
Table 2. Mesh independence verification of dual-propellant grain
网格序号 单元总数 最大压力/MPa 相对偏差/% 计算耗时/s 1 31631 13.040 −2.29 10 2 66855 13.163 −1.37 19 3 145517 13.243 −0.772 29 4 438052 13.310 −0.270 97 5 668894 13.346 178 注：采用3.2 GHz AMD Ryzen 7 5800H处理器完成计算；计算相对偏差时认为5号网格的最大压力为精确值。
下载: 导出CSV
-
[1] HARTFIELD R, JENKINS R, BURKHALTER J, et al. A review of analytical methods for solid rocket motor grain analysis[C]//Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Reston: AIAA, 2003: 4506. [2] TOLA C, NIKBAY M. Internal ballistic modeling of a solid rocket motor by analytical burnback analysis[J]. Journal of Spacecraft and Rockets, 2019, 56(2): 498-516. doi: 10.2514/1.A34065 [3] PETERSON E G, NIELSEN C C, JOHNSON W C, et al. Generalized coordinate grain design and internal ballistics evaluation program[C]//Proceedings of the 3rd Solid Propulsion Conference. Reston: AIAA, 1968: 490. [4] 梁国柱, 王慧玉. 三维装药几何通用型面模拟计算法[J]. 推进技术, 1991, 12(3): 26-35.LIANG G Z, WANG H Y. Generalized shape simulation method of three dimensional grain geometry[J]. Journal of Propulsion Technology, 1991, 12(3): 26-35 (in Chinese). [5] 鲍福廷, 李逢春, 徐东来. 固体发动机装药CAD[J]. 固体火箭技术, 1994, 17(3): 1-7.BAO F T, LI F C, XU D L. Computer aided design of propellant grains for solid rocket motors[J]. Journal of Solid Rocket Technology, 1994, 17(3): 1-7 (in Chinese). [6] 蔡强, 鲍福廷. 基于ACIS几何造型平台的固体火箭发动机装药设计[J]. 固体火箭技术, 2008, 31(3): 236-238. doi: 10.3969/j.issn.1006-2793.2008.03.008CAI Q, BAO F T. Grain design of solid rocket motor based on ACIS geometric modelling platform[J]. Journal of Solid Rocket Technology, 2008, 31(3): 236-238 (in Chinese). doi: 10.3969/j.issn.1006-2793.2008.03.008 [7] PÜSKÜLCÜ G, ULAS A. 3-D grain burnback analysis of solid propellant rocket motors: Part 2—Modeling and simulations[J]. Aerospace Science and Technology, 2008, 12(8): 585-591. doi: 10.1016/j.ast.2008.01.002 [8] WILLCOX M A, BREWSTER M Q, TANG K C, et al. Solid propellant grain design and burnback simulation using a minimum distance function[J]. Journal of Propulsion and Power, 2007, 23(2): 465-475. doi: 10.2514/1.22937 [9] REN P F, WANG H B, ZHOU G F, et al. Solid rocket motor propellant grain burnback simulation based on fast minimum distance function calculation and improved marching tetrahedron method[J]. Chinese Journal of Aeronautics, 2021, 34(4): 208-224. doi: 10.1016/j.cja.2020.08.052 [10] HEJL R J, HEISTER S D. Solid rocket motor grain burnback analysis using adaptive grids[J]. Journal of Propulsion and Power, 1995, 11(5): 1006-1011. doi: 10.2514/3.23930 [11] GUEYFFIER D, ROUX F X, FABIGNON Y, et al. High-order computation of burning propellant surface and simulation of fluid flow in solid rocket chamber[C]//Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. Reston: AIAA, 2014: 3612. [12] YILDIRIM C, AKSEL H. Numerical simulation of the grain burnback in solid propellant rocket motor[C]//Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston: AIAA, 2005: 4160. [13] SULLWALD W, SMIT G J, STEENKAMP A J, et al. Solid rocket motor grain burn back analysis using level set methods and Monte-Carlo volume integration[C]//Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. Reston: AIAA, 2013: 4087. [14] WANG D H, FEI Y, HU F, et al. An integrated framework for solid rocket motor grain design optimization[J]. Journal of Aerospace Engineering, 2014, 228(7): 1156-1170. doi: 10.1177/0954410013486589 [15] TOKER K, TINAZTEPE H, AKSEL M. Three-dimensional internal ballistic analysis by fast marching method applied to propellant grain burn-back[C]//Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston: AIAA, 2005: 4492. [16] MOKRÝ P. Iterative method for solving the eikonal equation[C]//Proceedings of the Optics and Measurement International Conference. Bellingham: SPIE, 2016: 1-6. [17] SETHIAN J A. Curvature and the evolution of fronts[J]. Communications in Mathematical Physics, 1985, 101(4): 487-499. doi: 10.1007/BF01210742 [18] MOUKALLED F, MANGANI L, DARWISH M. The finite volume method in computational fluid dynamics[M]. Berlin: Springer, 2016: 65-67. [19] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003: 27-28.WANG X C. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 27-28 (in Chinese). [20] CRANE K, WEISCHEDEL C, WARDETZKY M. Geodesics in heat: A new approach to computing distance based on heat flow[J]. ACM Transactions on Graphics, 2013, 32(5): 152. [21] CHURBANOV A G, VABISHCHEVICH P N. Numerical solving a boundary value problem for the eikonal equation[C]//Proceedings of the International Conference on Finite Difference Methods. Berlin: Springer, 2019: 28-34. [22] AVILA L S, AYACHIT U, BARRÉ S, et al. The VTK user's guide[M]. 11th ed. New York: Kitware, 2010: 485-486. [23] KING M. Analytical modeling of effects of wires on solid motor ballistics[C]//Proceedings of the 25th Joint Propulsion Conference. Reston: AIAA, 1989: 2784. -
下载:
点击查看大图
计量
- 文章访问数: 240
- HTML全文浏览量: 84
- PDF下载量: 2
- 被引次数: 0
