钢轨打磨车专用EHA非线性反演控制

王海波; 何欢; 邹怀静; 聂勇

doi:10.13700/j.bh.1001-5965.2022.0681

钢轨打磨车专用EHA非线性反演控制

doi: 10.13700/j.bh.1001-5965.2022.0681

王海波^{1, 2, ,},
何欢¹,
邹怀静¹,
聂勇³

1.
西南交通大学机械工程学院，成都 610031
2.
轨道交通运维技术与装备四川省重点实验室，成都 610031
3.
浙江大学流体传动及控制国家重点实验室，杭州 310027

基金项目: 四川省科技厅计划应用基础研究项目(2021YJ0029)；西南交通大学轨道交通运维技术与装备四川省重点实验室开放课题(2020YW001)

详细信息

通讯作者:
E-mail：haibowang@home.swjtu.edu.cn

中图分类号: U216；TH137
计量
- 文章访问数: 242
- HTML全文浏览量: 121
- PDF下载量: 7
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-01
- 录用日期: 2022-10-30
- 网络出版日期: 2022-11-15
- 整期出版日期: 2024-08-28

Nonlinear backstepping control of special EHA for rail grinding vehicles

WANG Haibo^{1, 2
, ,},
HE Huan¹,
ZOU Huaijing¹,
NIE Yong³

1.
School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China
2.
Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province，Chengdu 610031，China
3.
State Key Laboratory of Fluid Power Transmission and Control，Zhejiang University，Hangzhou 310027，China

Funds: Science and Technology Department's Planned Application Basic Research Project of Sichuan Porvince(2021YJ0029); Open Research Project of Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of South West Jiaotong University (2020YW001)

More Information

Corresponding author: E-mail：haibowang@home.swjtu.edu.cn

摘要

摘要:
为提高钢轨打磨车打磨钢轨的平顺性及稳定性，提出以电动静液作动器(EHA)代替传统液压作动系统作为钢轨打磨车的专用执行器，考虑柱塞泵的总效率波动和液压缸动静摩擦差异大2个非线性因素，建立非线性数学模型；建立EHA的MATLAB、AMESim联合仿真模型，对PID控制、滑模变结构控制、反演控制进行控制策略对比研究，仿真分析验证反演控制在响应快速性及稳定性方面具有良好的表现。搭建四象限平台对EHA进行反演控制负载试验，结果表明：其位移控制精度达0.21 mm，具有较好的控制性能。
- 钢轨打磨车 /
- 电动静液作动器 /
- 非线性因素 /
- 联合仿真 /
- 反演控制
Abstract:
In order to improve the smoothness and stability of rail grinding by the rail grinding vehicle, an electric hydrostatic actuator (EHA) was proposed to replace the traditional hydraulic system as the special actuator of the rail grinding vehicle. By considering the nonlinear factors including the total efficiency fluctuation of the plunger pump and the large difference between the dynamic and static friction of the hydraulic cylinder, a nonlinear mathematical model was established. The MATLAB and AMESim joint simulation model of EHA was established, and the control strategies of PID control, sliding mode variable structure control, and backstepping control were compared. The simulation analysis verified that the backstepping control had good performance in response speed and stability. The four quadrant platform was built to carry out the backstepping control load test of EHA. The results show that its displacement control accuracy reaches 0.21 mm, indicating good control performance.
- rail grinding vehicle /
- electric hydrostatic actuator /
- nonlinear factors /
- joint simulation /
- backstepping control

HTML全文

截至2020年，中国铁路线路运营总里程已突破1.5×10⁵ km，稳居世界第2^[1]。铁路工程项目运营后，科学、合理和经济的运营维护是保证列车行车及乘员和货物安全的必要手段。在铁路和城市轨道维护工作中，钢轨打磨车可有效消除钢轨的肥边、裂纹及磨耗等损坏，确保列车运行的安全可靠性^[2-3]。钢轨打磨车存在打磨工艺精度要求高、打磨工况复杂、打磨机构作动不够平稳、打磨头需要反复标定等问题，传统液压作动系统已无法在可靠性、可维护性及控制性之间平衡矛盾，影响钢轨打磨的平顺性及稳定性^[4-6]。因此，拟采用已在飞机、潜艇、导弹等大型装备上获得广泛应用的功率电传系统，利用电动静液作动器（electro-hydrostatic actuator，EHA）代替钢轨打磨车打磨装置集中能源式液压作动系统，驱动功率通过电缆传送到钢轨打磨车各处的打磨装置驱动油缸，将电能转化为机械能，驱动钢轨打磨车打磨电机的升降和打磨头角度的偏转，十分契合钢轨打磨车等铁路线路大型运维装备的作业工况。并结合打磨车打磨工艺的要求和施工作业的工况探索研究适宜的控制策略，使EHA满足钢轨打磨车应用领域的性能需求，实现打磨工艺及施工效率的提升。

从控制算法层面考虑，如何提高控制精度、改善EHA性能也是众多学者研究的重点，熊志林等^[7]基于状态估计与模型预测理论设计的泵控非对称缸控制器，稳态误差约0.5 mm；纪铁铃等^[8]针对EHA位置控制环设计滑模变结构控制器，通过联合仿真验证控制器提高了系统动态响应性，具有较高的稳态精度；付永领等^[9]以数字信号处理器（digital signal processor，DSP）和复杂可编程逻辑器件（complex programmable logic device，CPLD）为核心设计双余度控制器，实现了快速稳定的跟踪需求；张星晴和段富海^[10]建立EHA调速控制模型，采用遗传算法得到PID调节器最优参数，仿真结果超调量小于5%。

实际上，EHA存在泵的流量压力脉动、泵的总效率波动、液压缸动静摩擦差异大、油液特性参数变化等诸多非线性因素，全部做简单的线性化处理，结论与实际工作情况有较大差别，且无法解释很多实际工作过程中的异常现象，因此，非线性因素研究十分必要。而反演控制是一种较新的、应用较广泛的针对非线性系统的控制策略^[11]，其应用能够极大地减少非线性因素对EHA系统控制性能的影响。因此，本文将对反演控制对EHA系统控制性能的影响进行研究。

1. EHA的数学模型

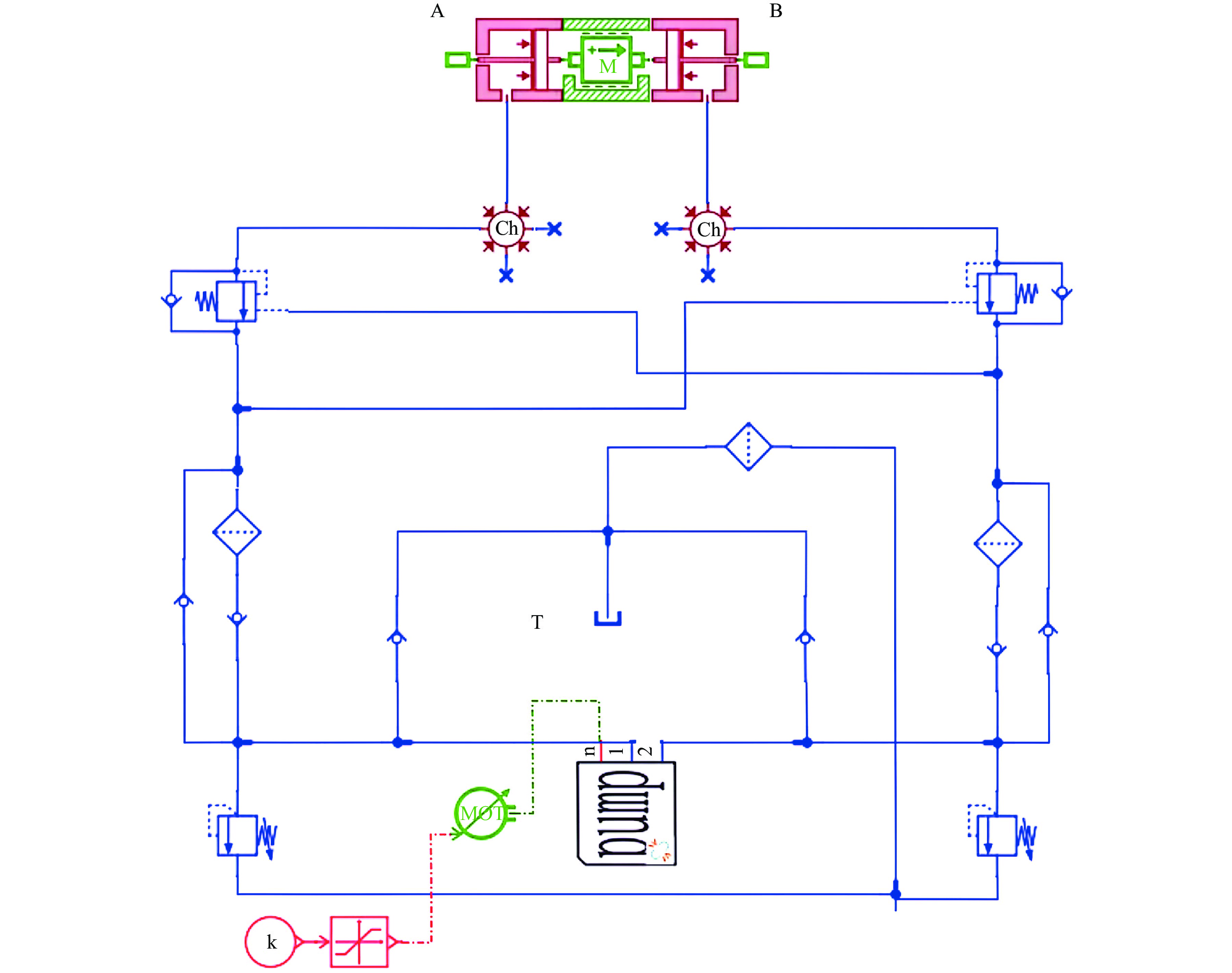
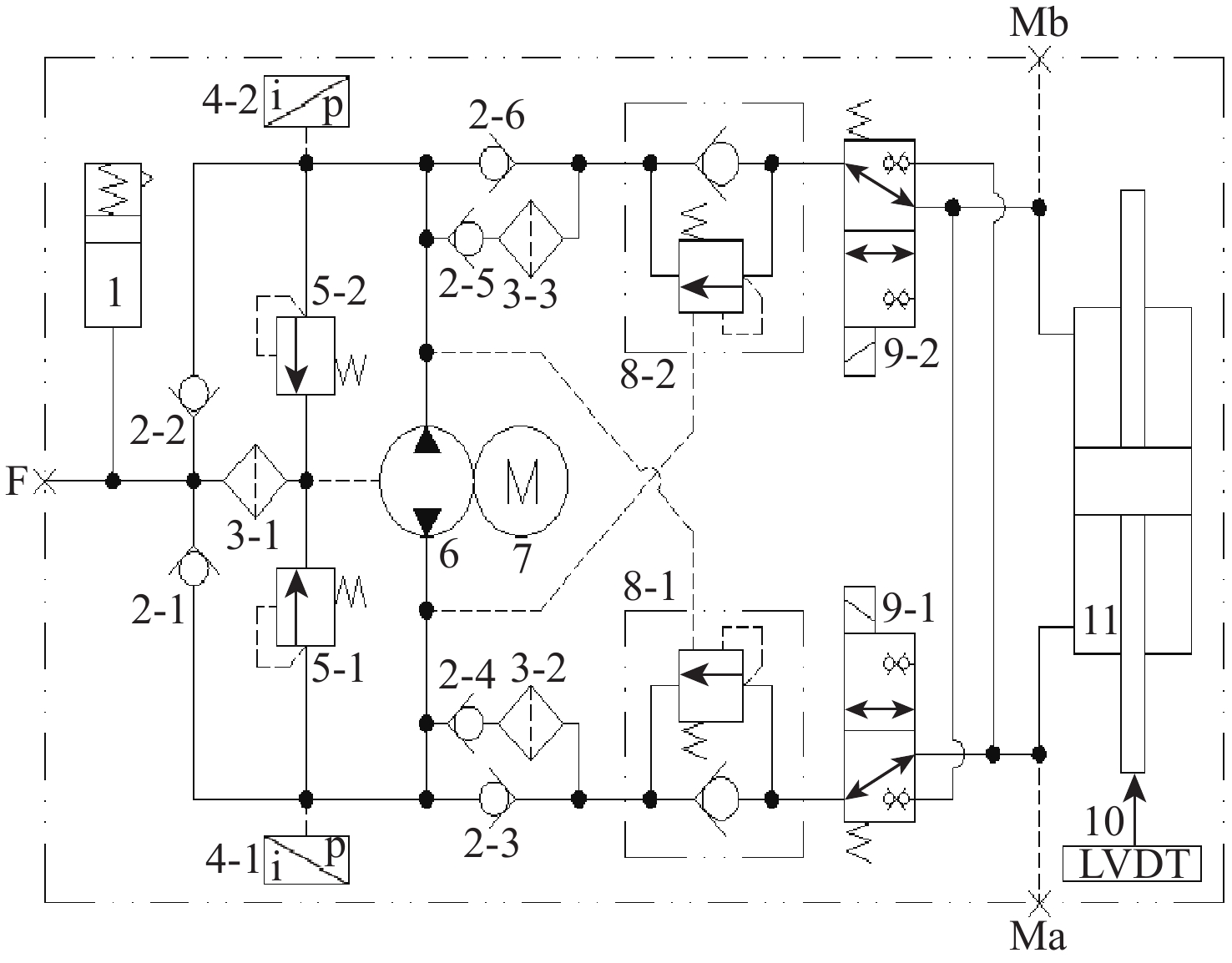
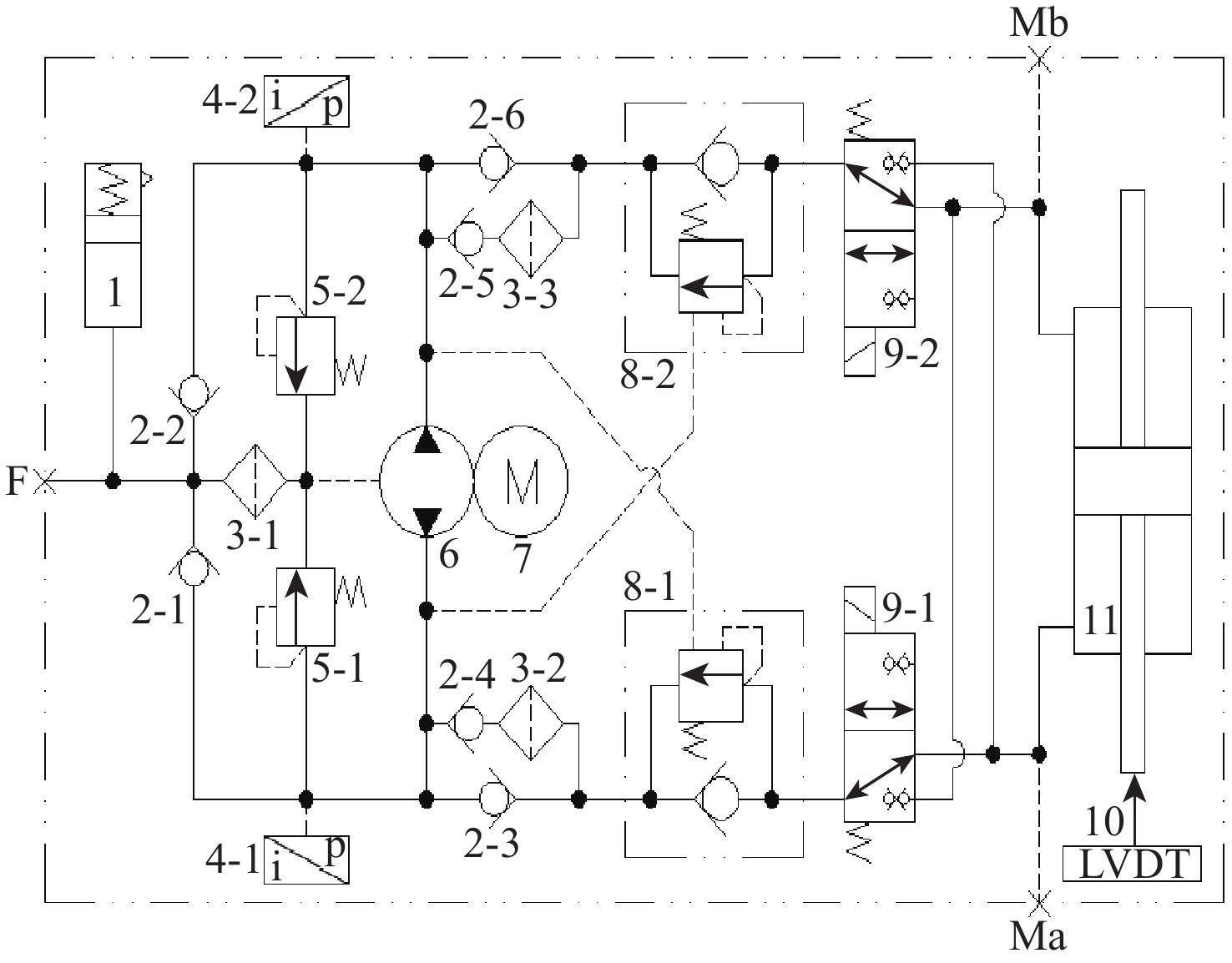
综合打磨头角度偏转和打磨电机避障升降2种工况的需求，查阅文献[12]根据指标计算，考虑到EHA试验样机制作的经济性，设定EHA设计参考数据如表1所示，以设计一台EHA原理样机满足工况需求试验验证，其液压原理如图1所示，采用双向定排量变转速泵驱动双作用对称缸，在液压缸内设置直线位移传感器（linear variable displacement transducer，LVDT）实时反馈位移信号，以交流伺服电机作为控制输入，实现EHA的往复作动，其中，Mb和Ma为传感器预留接口。

表 1 EHA设计指标

Table 1. Design indexes of EHA

行程/mm	负载力/KN	速度/（mm·s⁻¹）	位移全尺寸精度/%
100	≤10	≥20	≤0.77

下载: 导出CSV

| 显示表格

图 1 专用EHA液压原理

1. 弹簧增压油箱；2. 单向阀；3. 过滤器；4. 压力变送器；5. 溢流阀；6. 双向定排量变转速泵；7. 伺服电机；8. 平衡阀；9. 电磁换向阀；10. 位移传感器；11. 双作用对称缸。

Figure 1. Hydraulic principle of special EHA

下载: 全尺寸图片幻灯片

1.1 永磁同步电机与泵控缸模型

假设铁芯饱和效应、产生的涡流、损耗可以忽略^[13]。根据d轴电流 ${{{i}}_{{d}}}{{ = 0}}$ 矢量控制方法，由电流及电压关系得电机q轴定子电压方程：

$U = {{{i}}_{{q}}}{{{R}}_{\rm{a}}}{{ + }}\frac{{{\rm{d}}{{{i}}_{{q}}}}}{{{{{\mathrm{d}}t}}}}{{{L}}_{{q}}} + \omega {{{\varphi }}_{\rm{f}}}$

(1)

式中： $U$ 为电机电压； ${{{R}}_{{{\mathrm{a}}}}}$ 为绕组等效电阻； ${{{i}}_{{q}}}$ 为q轴电流； ${{{L}}_{{q}}}$ 为等效q轴电感； ${\omega}$ 为转子角速度； ${{{\varphi }}_{{{\mathrm{f}}}}}$ 为电机永磁体磁链。

电机电磁转矩方程为

${{{T}}_{{\mathrm{em}}}} = \frac{3}{2}{{{P}}_{{{\mathrm{n}}}}}{{{i}}_{{q}}}{{{\varphi }}_{{{\mathrm{f}}}}}$

(2)

式中： ${{{T}}_{{\mathrm{em}}}}$ 为电机电磁转矩； ${{{P}}_{{{\mathrm{n}}}}}$ 为电机极对数。

电机运动平衡方程为

${{{T}}_{{\mathrm{em}}}} = \frac{{{J}}}{{{{{P}}_{\rm{n}}}}}\cdot \frac{{{{{\mathrm{d}}\omega }}}}{{{{{\mathrm{d}}t}}}} + B \frac{{{\omega}}}{{{{{p}}_{\rm{n}}}}} + {{{T}}_{{{\mathrm{L}}}}}$

(3)

式中： ${{J}}$ 为转动惯量； ${{B}}$ 为电机与泵的黏性摩擦系数和； ${{{T}}_{\rm{L}}}$ 为电机的负载转矩。

忽略液压缸的压力损失及内外泄漏，油温为常数，则液压缸的流量连续性方程为

$Q = {{{A}}_{{{\mathrm{P}}}}}\frac{{{{{\mathrm{d}}}}{{{x}}_{{{\mathrm{p}}}}}}}{{\mathrm{d}}t} + \frac{{{{{V}}_{{1}}}}}{{{{{\beta}}_{{{\mathrm{e}}}}}}}\cdot\frac{{{{{\mathrm{d}}}}{{{p}}_{{{\mathrm{L}}}}}}}{{{{{\mathrm{d}}t}}}}= {{{q}}_{{{\mathrm{L}}}}}$

(4)

式中： ${{{q}}_{\rm{L}}}$ 为负载流量； ${{{p}}_{\rm{L}}}$ 为液压缸油液压差； ${{{A}}_{\rm{P}}}$ 为活塞面积； ${{{x}}_{\rm{P}}}$ 为活塞位移； ${{{\beta}}_{\rm{e}}}$ 为体积弹性模量； ${{{V}}_{{1}}}$ 为进油腔容积。

根据EHA在钢轨打磨车上的应用工况分析，弹性负载可忽略^[14]，其输出力与负载力平衡方程为

${{{A}}_{\rm{p}}}{{{p}}_{\rm{L}}} = {{{m}}_{\rm{t}}}\frac{{{{\mathrm{d}}^2}{{{x}}_{\mathrm{P}}}}}{{{\mathrm{d}}{t^2}}} + {{{B}}_{\rm{p}}}\frac{{{\mathrm{d}}{{{x}}_{\mathrm{P}}}}}{{{\mathrm{d}}t}} + {{{F}}_{\rm{L}}}$

(5)

式中： ${{{m}}_{\rm{t}}}$ 为活塞总质量； ${{{B}}_{\rm{P}}}$ 为黏性阻尼系数； ${{{F}}_{\rm{L}}}$ 为外负载与摩擦力。

1.2 非线性参数理论建模

1.2.1 柱塞泵效率

轴向柱塞泵的总效率为

$\eta = {\eta _V}{\eta _{\mathrm{m}}}$

(6)

式中： $\eta$ 为总效率； ${\eta _V}$ 为容积效率； ${\eta _{\mathrm{m}}}$ 为机械效率。柱塞泵总效率的非线性影响是柱塞泵的容积效率造成的，柱塞泵的机械效率变化幅度不大^[15]。分析柱塞泵容积效率的非线性影响，建立其数学模型。

柱塞泵的容积效率非线性影响主要由柱塞泵的容积损失引起，容积损失 ${Q_V}$ 由摩擦副泄漏 ${Q_{\mathrm{L}}}$ 和油液压缩 ${Q_{\mathrm{C}}}$ 组成，可表示为

${Q_V} = \sum {{Q_{{\mathrm{L}}i}} + {Q_{\mathrm{C}}}}$

(7)

其中，内部摩擦副的泄漏损失包括柱塞副、滑靴副和配流副的泄漏损失。柱塞副泄漏的损失 ${Q_{{\mathrm{L}}1}}$ 表示为

${Q_{{\mathrm{L}}1}} = \sum\limits_{i = 0}^{{\textit{z}} - 1} {\frac{{{\text{π}} {{{d}}_{\rm{P}}}\delta _{\rm{P}}^3\Delta {p_{{\mathrm{p}}i}}}}{{12\mu {L_i}}}} (1 + 1.5{\varepsilon ^2})$

(8)

式中： ${{{d}}_{\rm{P}}}$ 为柱塞直径； ${\delta _{\mathrm{P}}}$ 为柱塞与柱塞孔间隙； $\Delta {p_{{\mathrm{P}}i}}$ 为第 $i$ 个柱塞腔内外压差； $\mu$ 为油液动力黏度； $\varepsilon$ 为偏心率； ${L_i}$ 为柱塞与缸体接触长度。

滑靴副的泄漏损失 ${Q_{{\mathrm{L}}2}}$ 表示为

${Q_{{\mathrm{L}}2}} = \frac{{{\textit{z}}{\text{π}} \delta _{\mathrm{s}}^3}}{{12\mu \ln \dfrac{{{R_{{\mathrm{s}}2}}}}{{{R_{{\mathrm{s}}1}}}}}}({p_1} - {p_0})$

(9)

式中： ${\textit{z}}$ 为柱塞个数； $\delta _{\mathrm{s}}$ 为滑靴副间隙油膜厚度； ${R_{{\mathrm{s}}1}}$ 、 ${R_{{\mathrm{s}}2}}$ 为滑靴封油带内外半径； ${p_0}$ 、 ${p_1}$ 为泵进出口油液压力。

配流副的泄漏损失 ${Q_{{\mathrm{L}}3}}$ 表示为

${Q_{{\mathrm{L}}3}} = \frac{{{\varphi _0}\delta _{\mathrm{v}}^3}}{{12\mu }}\left( {{1}\bigg/{{\ln \dfrac{{{R_{{\mathrm{v}}4}}}}{{{R_{{\mathrm{v}}3}}}}}}} \right. + \left. {{1}\bigg/{{\ln \dfrac{{{R_{{\mathrm{v}}2}}}}{{{R_{{\mathrm{v}}1}}}}}}} \right)\left( {{p_1} - {p_0}} \right)$

(10)

式中： ${\varphi _0}$ 为配流盘高压排油区封油带包角； $\delta _{\mathrm{v}}^{}$ 为配流副油膜厚度； ${R_{{\mathrm{v}}1}}$ 、 ${R_{{\mathrm{v}}2}}$ 为配流盘内封油带内外半径； ${R_{{\mathrm{v}}3}}$ 、 ${R_{{\mathrm{v}}4}}$ 为配流盘外封油带内外半径。

油液压缩导致的流量损失 ${Q_{\mathrm{C}}}$ 为

${Q_{\mathrm{C}}} = \frac{{n{\textit{z}}{V_{\mathrm{f}}}}}{{60E}}\left( {{p_1} - {p_0}} \right)$

(11)

式中： $n$ 为柱塞泵转速； ${V_{\mathrm{f}}}$ 为单柱塞排量； $E\mathrm{为}$ 液压油弹性模量。

柱塞泵的理论流量 ${Q_{\mathrm{T}}}$ 表示为

${Q_{\mathrm{T}}} = {{{{{D}}_{\rm{P}}}{{n}}}}/{{{{60}}}}$

(12)

式中： ${{{D}}_{\rm{P}}}$ 为柱塞孔分布圆直径。

则柱塞泵的容积效率 ${\eta _V}$ 表示为

${\eta _V} = \frac{{{Q_{\mathrm{T}}} - {Q_V}}}{{{Q_{\mathrm{T}}}}} = 1 - \frac{{\displaystyle\sum {{Q_{{\mathrm{L}}i}} + {Q_{\mathrm{C}}}} }}{{{Q_{\mathrm{T}}}}}$

(13)

将柱塞泵内部结构及油液参数代入式(13)，选取机械效率 ${\eta _{\mathrm{m}}} = 0.92$ ，因此，柱塞泵的总效率为

$\eta = 0.92 - \frac{{102.33\left( {{p_1} - {p_2}} \right) + 0.09\left( {{p_1} - {p_2}} \right)n}}{{1\;000n}}$

(14)

1.2.2 液压缸摩擦力

液压缸活塞与缸筒之间因为密封及液压缸材质不一致，且存在橡胶等摩擦力极大的材料，开始运动的静摩擦力与液压缸运动时的动摩擦力相差极大，呈现非线性特征。由液压缸存在的Streibeck效应粗略地表示了润滑状态与摩擦因素的关系^[16]。

采用Canudas de Wit等^[17]提出的LuGre液压缸非线性摩擦力模型：

$\left\{ \begin{gathered} {{f}} = {\sigma _0}{\textit{z}_{0}} + {\sigma _1}\frac{{{\mathrm{d}}{\textit{z}_{0}}}}{{{\mathrm{d}}t}} + {\sigma _2}{{v}} \\ \frac{{{\mathrm{d}}{\textit{z}}_{0}}}{{{\mathrm{d}}t}} = v - \frac{{\left| v \right|}}{{g\left( v \right)}}{\textit{z}_{0}} \\ {\sigma _0}g\left( {{v}} \right) = {{{f}}_{\mathrm{s}}} + \left( {{{{f}}_{\mathrm{s}}} - {{{f}}_{\mathrm{c}}}} \right){{\mathrm{e}}^{ - {{\left( {{v /{{v_{\mathrm{s}}}}}} \right)}^2}}} \\ \end{gathered} \right.$

(15)

式中： ${\textit{z}_0}$ 为鬃毛挠度； ${\sigma _0}$ 为鬃毛刚度； ${\sigma _1}$ 为鬃毛阻尼系数； ${\sigma _2}$ 为黏性摩擦因素； ${v_{\mathrm{s}}}$ 为摩擦Streibeck临界速度； $g\left( {{v}} \right)$ 为摩擦Streibeck曲线函数； ${{{f}}_{\mathrm{c}}}$ 为库仑摩擦力； ${{{f}}_{\mathrm{s}}}$ 为静摩擦力。LuGre摩擦力模型的一些参数难以通过实验测试，基于文献[18]经验估计及样机空载实验数据计算，相关参数取值如表2所示。

表 2 摩擦模型相关参数

Table 2. Relevant parameters of friction model

${{{\sigma _0}} / ({{\mathrm{N}} \cdot {\mathrm{m}}}})$	${{{\sigma _1}} /( {{\mathrm{N}} \cdot {\mathrm{m}}}} \cdot {{\mathrm{s}}^{ - 1}})$	${{{\sigma _2}} /( {{\mathrm{N}} \cdot {\mathrm{m}} \cdot {{\mathrm{s}}^{ - 1}}}})$	${{{v_{\mathrm{s}}}} /({{\mathrm{N}} \cdot {\mathrm{m}} \cdot {{\mathrm{s}}^{ - 1}}}})$	${{ {{f_{\mathrm{c}}}} } /{{\mathrm{kN}}}}$	${{ {{f_{\mathrm{s}}}} }/ {{\mathrm{kN}}}}$
$2.1\times {10}^{7}$	0.1	150	0.1	142	12

下载: 导出CSV

| 显示表格

经计算，液压缸的最大运动速度为0.023 m/s，利用计算机技术在相对运动速度为0～0.023 m/s的区间对微分方程组进行拟合，得到EHA液压缸的非线性摩擦力为

${{f}} = 165.66 - {{164.78}}\bigg/\left[{{1 + {{\left( {\dfrac{{{v}}}{{0.02}}} \right)}^{2.28}}}}\right]$

(16)

2. 反演控制器设计

根据EHA的数学模型，选取系统状态变量为：位移、速度和进油腔压力，可表示为

${\boldsymbol{X}} = \left[ \begin{gathered} {{{x}}_1} \\ {{{x}}_2} \\ {{{x}}_3} \\ \end{gathered} \right] = \left[ \begin{gathered} {{x}} \\ {\dot {{x}}} \\ {{{p}}_1} \\ \end{gathered} \right]$

(17)

式中： ${{{x}}_1}$ 为位移； ${{{x}}_2}$ 为速度； ${{{x}}_3}$ 为进油腔压力。则EHA液压系统转化为三阶系统，控制变量为电机转速 ${\omega _{\mathrm{e}}}$ ，输出变量为EHA位移 $x$ ，其非线性状态空间模型可表示为

$\left\{ \begin{gathered} {{\dot {{x}}}_1} = {{{x}}_2} \\ {{\dot {{x}}}_2} = \frac{{{A_{\rm{p}}}}}{M}{{{x}}_3} - \frac{{{A_{\rm{P}}}}}{M}{p_0} - \frac{{{B_{\rm{P}}}}}{M}{{{x}}_2} - \frac{{{F_{\mathrm{L}}}}}{M} \\ {{\dot {{x}}}_3} = \frac{{\omega {D_{\rm{p}}}\eta {\beta _{\rm{e}}}}}{{{V_1}}} - \frac{{{\beta _{\rm{e}}}{A_{\rm{p}}}}}{{{V_1}}}{{{x}}_2} \\ {{y}} = {{{x}}_1} \\ \end{gathered} \right.$

(18)

在反演控制器设计过程中，令 ${{{e}}_i}$ 表示状态量实际值与期望值的跟踪误差， ${{{x}}_{i{\mathrm{d}}}}$ 为状态量的期望输出，有

$\left\{ \begin{gathered} {{{e}}_1} = {{{x}}_1} - {{{x}}_{1{\mathrm{d}}}} \\ {{{e}}_2} = {{{x}}_2} - {{{x}}_{2{\mathrm{d}}}} \\ {{{e}}_3} = {{{x}}_3} - {{{x}}_{3{\mathrm{d}}}} \\ \end{gathered} \right.$

(19)

从最远离控制输入的方程开始进行递推，对第1个子系统而言，控制目标是使 ${{{x}}_1}$ 的实际值趋近于期望值 ${{{x}}_{1{\mathrm{d}}}}$ ，即 ${{{e}}_1}$ 趋近于0， ${{{x}}_{1{\mathrm{d}}}}$ 作为设定值已知，构造李雅普诺夫函数：

${V_{{{{e}}_1}}} = \frac{1}{2}{{e}}_1^2$

(20)

选取虚拟控制函数：

${\dot {{x}}_1} - {\dot {{x}}_{1{\mathrm{d}}}} = - {k_1}{{{e}}_1}$

(21)

式中： ${k}_{1}＞0$ ，则由式（20）和式（21）可得

$\dot{V}\left({{e}}_{1}\right)={{e}}_{1}{\dot{e}}_{1}=-{k}_{1}{{e}}_{1}^{2}＜0$

(22)

满足系统滑模面的李雅普诺夫条件，同理，对第2个子系统方程研究， ${{{e}}_2}$ 趋近于0， ${{{x}}_{2{\mathrm{d}}}}$ 选取第1步子系统虚拟控制器得到的函数值，由式（21）可得

${{{x}}_{2{\mathrm{d}}}} = {\dot {{x}}_1} = {\dot {{x}}_{1{\mathrm{d}}}} - {k_1}{{{e}}_1}$

(23)

将第1、第2个子系统方程结合起来构造系统李雅普诺夫函数为

$V\left( {{{{e}}_1},{{{e}}_2}} \right) = \frac{1}{2}{{e}}_1^2 + \frac{1}{2}{{e}}_2^2$

(24)

选取虚拟控制函数：

${\dot {{x}}_2} - {\dot {{x}}_{2{\mathrm{d}}}} = - {k_2}{{{e}}_2}$

(25)

式中： ${k_2}$ >0，则由式（24）和式（25）可得

$\dot{V}\left({{e}}_{1},{{e}}_{2}\right)={{e}}_{1}{\dot{{{e}}}}_{1}+{{e}}_{2}{\dot{{{e}}}}_{2}=-{k}_{1}{{e}}_{1}^{2}-{k}_{2}{{e}}_{2}^{2}<{{0}}$

(26)

满足系统滑模面的李雅普诺夫条件，同理，对第3个子系统方程研究， ${{{e}}_3}$ 趋近于0， ${{{x}}_{3{\mathrm{d}}}}$ 选取第2步子系统虚拟控制器得到的函数值，由式（18）和式（25）可得

${{{x}}_{3{\mathrm{d}}}} = \left( {{{\dot {{x}}}_{2{\mathrm{d}}}} - {k_2}{{{{e}}} _2} + \frac{{{A_{\rm{p}}}}}{M}{p_0} + \frac{{{B_{\rm{p}}}}}{M}{{{{x}}} _2} + {{{{F}}} _{\mathrm{L}}}} \right) \frac{M}{{{A_{\rm{p}}}}}$

(27)

将第1、第2、第3个子系统方程结合起来构造系统李雅普诺夫函数：

${V} \left( {{{{e}}_1},{{{e}}_2},{{{e}}_3}} \right) = \frac{1}{2}{{e}}_1^2 + \frac{1}{2}{{e}}_2^2 + \frac{1}{2}{{e}}_3^2$

(28)

选取虚拟控制函数：

${\dot {{x}}_3} - {\dot {{x}}_{3{\mathrm{d}}}} = - {k_3}{{{e}}_3}$

(29)

式中： ${k_3}$ >0，则由式（28）和式（29）可得

$\dot{V}\left({{e}}_{1},{{e}}_{2},{{e}}_{3}\right)={{e}}_{1}{\dot{{{e}}}}_{1}+{{e}}_{2}{\dot{{{e}}}}_{2}+{{e}}_{3}{\dot{{{e}}}}_{3}=-{k}_{1}{{e}}_{1}^{2}-{k}_{2}{{e}}_{2}^{2}-{k}_{3}{{e}}_{3}^{2}<{{0}}$

(30)

满足系统滑模面的李雅普诺夫条件，根据式（18）、式（21）、式（25）和式（29），可得系统的控制函数为

$\begin{split} &\omega \left( t \right) = \frac{{{V_1}}}{{{D_{\rm{p}}}\eta {\beta _{\rm{e}}}}}\left. \left\{ {\frac{{{A_{\rm{p}}}{\beta _{\rm{e}}}}}{{{V_1}}}} \right.{{\dot {{x}}}_1} - {k_3}{{{e}}_3} + \right.\\ &\quad\quad\left.\frac{M}{{{A_{\rm{p}}}}}\left[ {\frac{{{A_{\rm{P}}}}}{M}{p_0} + \frac{{{B_{\rm{p}}}}}{M}{{\dot {{x}}}_2} + \frac{{{F_L}}}{M} - {k_2}{{\dot {{e}}}_2} + \left( {{{\ddot {{x}}}_{1{\mathrm{d}}}} - {k_1}{{\dot {{e}}}_1}} \right)} \right] \right\} \end{split}$

(31)

式中： ${k_1}$ 、 ${k_2}$ 、 ${k_3}$ 为系统反演控制器的控制参数，影响系统响应的快速性、稳定性及是否超调，位移状态量和进油口压力状态量由系统自带的位移传感器与压力变送器测量给出实际数值，速度状态量既可由位移状态量一阶微分得出，亦可采用状态观测器推导得出，非线性参数由1.2节推导给出。

3. 联合仿真

3.1 钢轨打磨车专用EHA仿真建模

为验证控制策略的有效性，结合AMEsim与MATLAB/Simulinkl这2种软件的优势进行联合仿真，使用AMESim软件中的液压库、信号库等建立含有Simulink模块的液压系统仿真模型，将液压泵的模型使用超级元件封装进行处理^[19]。

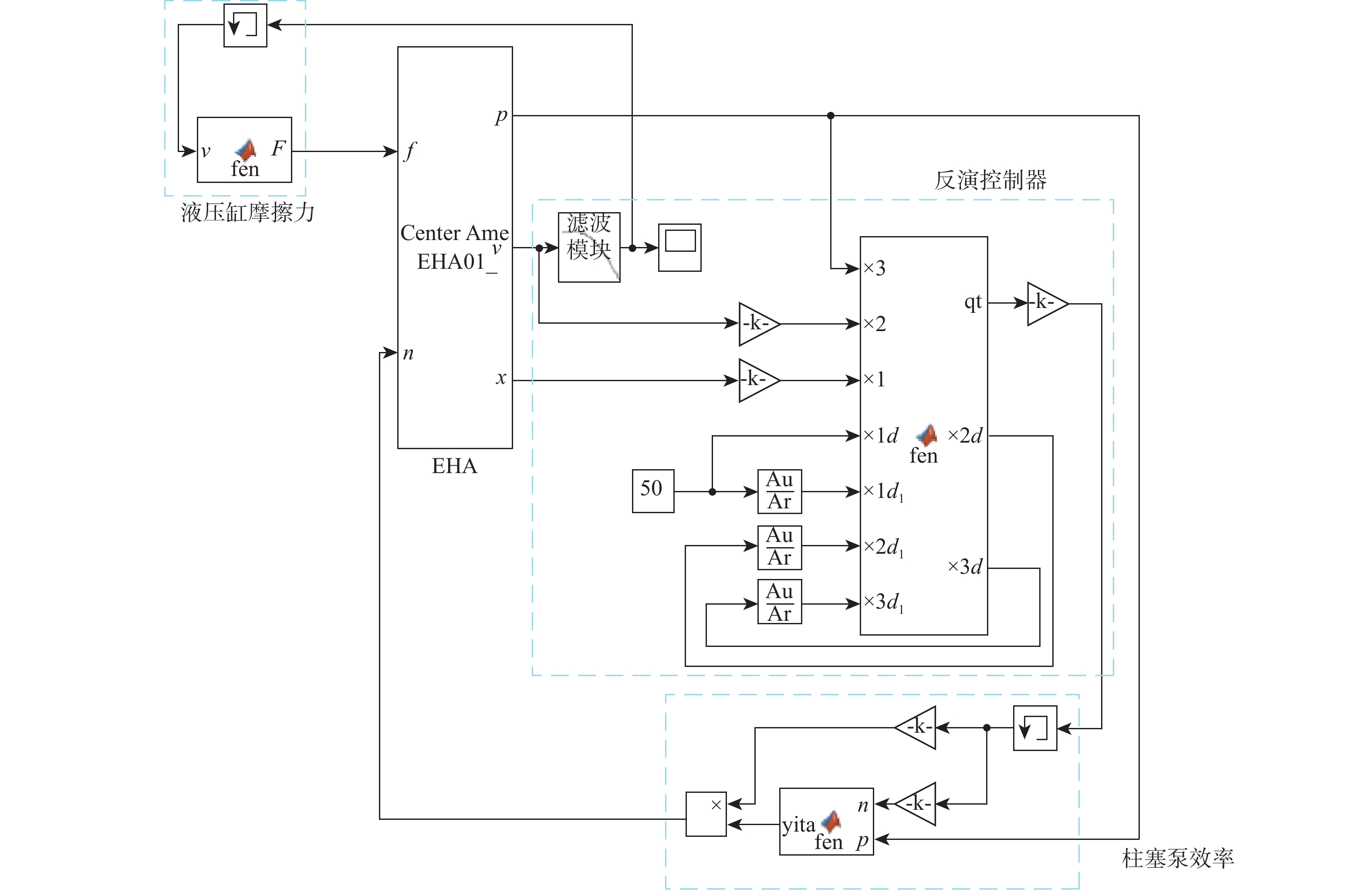
本文控制系统的输入为EHA作动缸的目标位移，输出为电机转速，闭环反馈为EHA的实际位移及根据算法所需的特殊中间变量。基于式（31），运用Simulink建立反演控制器的仿真模型，并引入柱塞泵效率和液压缸摩擦力2项非线性影响因素。采用Simulink中S-Function的调用语法与AMEsim中的求解器进行交互^[20]。仿真软件所设参数如表3所示，建立EHA的反演控制系统模型如图2所示，联合仿真模型如图3所示，其中，f表示液压缸摩擦力，p表示液压缸进油腔压力，v表示液压缸速度，fen表示仿真软件的运算模块，k表示增益模块，n表示转速，A表示油缸A腔，B表示油缸B腔，T表示油箱，X表示位移传感器，V表示速度传感器，T表示力传感器，K表示控制信号，ch表示成腔容积或无效容积。

表 3 EHA仿真参数

Table 3. Simulation parameters of EHA

参数	数值
油缸有效行程/mm	100
油缸直径/mm	63
活塞杆直径/mm	35
泵额定转速/（r·min⁻¹）	3000
泵排量/(ml·r⁻¹)	1
溢流压力/MPa	8
转子惯量/( $\mathrm{k}\mathrm{g}\cdot{{\mathrm{m}}}^{2}$ )	$2.7\times {10}^{-5}$
线电阻/Ω	5.5
线电感/H	$9.6\times {10}^{-3}$
反电势常数/( $\mathrm{V}\cdot \mathrm{m}\cdot {{\mathrm{r}}}^{-1}$ )	$3.2\times {10}^{-2}$

下载: 导出CSV

| 显示表格

图 2 EHA的反演控制系统模型

Figure 2. Backstepping control system model of EHA

下载: 全尺寸图片幻灯片

图 3 EHA的联合仿真模型

Figure 3. Joint simulation model of EHA

下载: 全尺寸图片幻灯片

3.2 控制策略仿真分析

联合仿真以AMESim液压仿真为主，通过传感采集元件将液压缸位移、速度和进油腔压力反馈给Simulink控制系统，Simulink控制子系统通过控制算法，计算输出控制驱动电机的转速及作用于液压缸内部的非线性摩擦力，反馈回AMESim主仿真系统。

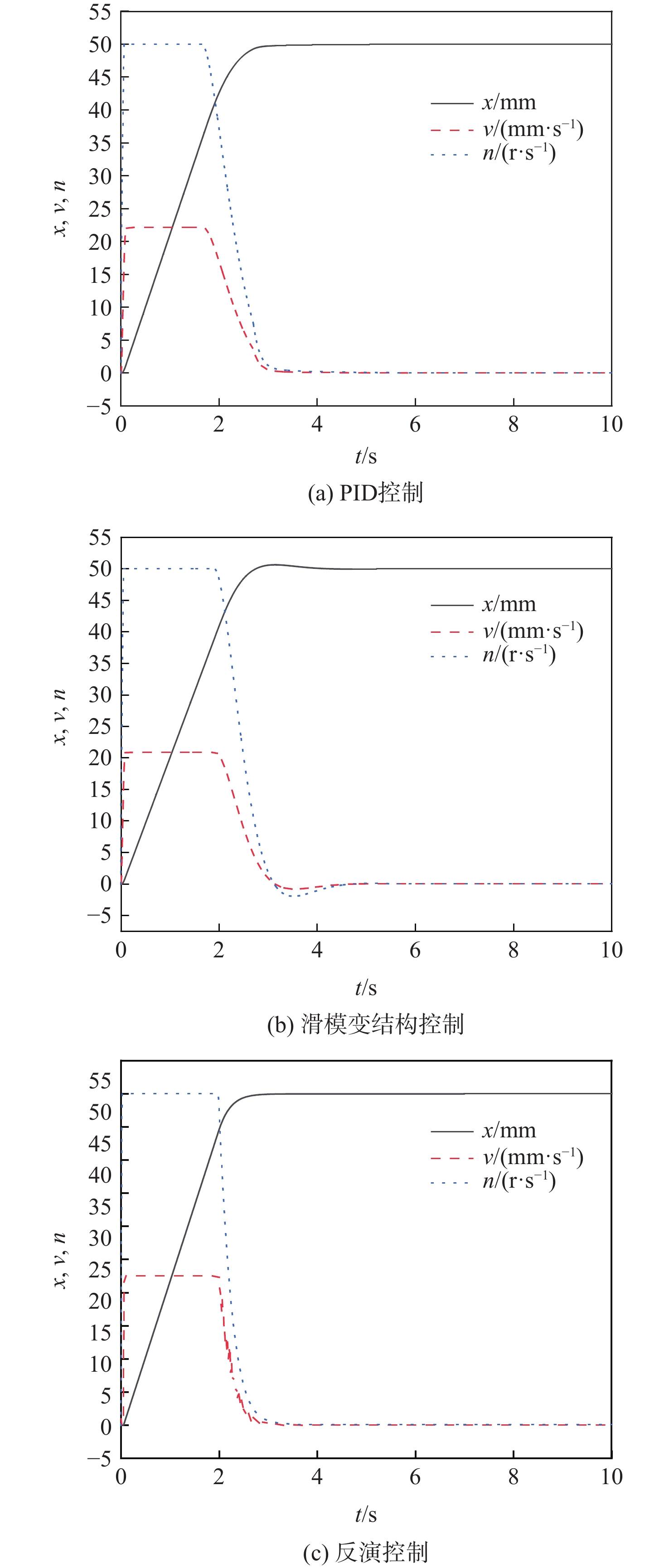
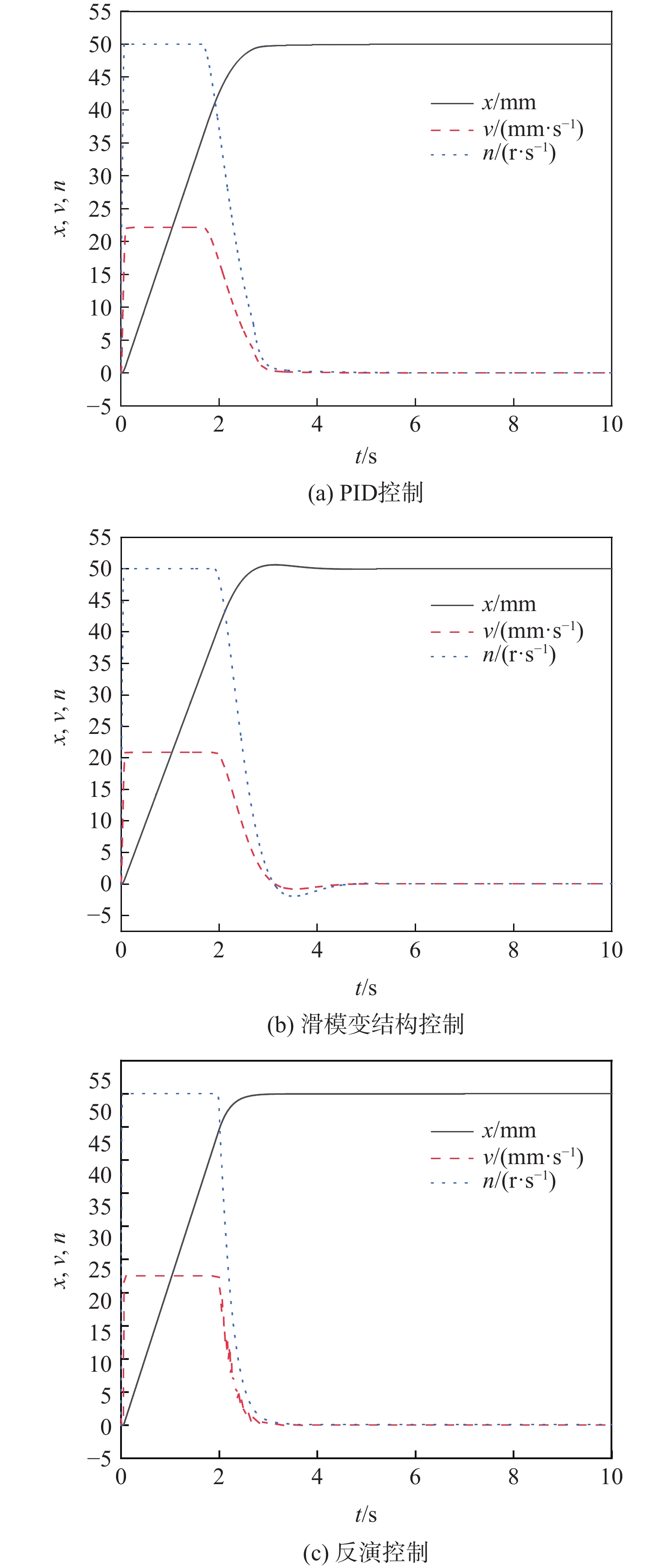
考虑柱塞泵效率、液压缸摩擦力等非线性因素的影响，对PID控制、滑模变结构控制、反演控制策略进行联合仿真试验，如图4所示，发现可靠的控制策略，便于进行样机试验。

图 4 不同控制策略仿真结果

Figure 4. Simulation results of different control strategies

下载: 全尺寸图片幻灯片

基于联合仿真模型，在控制系统不发生超调的前提下尽可能提高系统的快速响应性，PID控制系统代表参数 ${k_{\rm{P}}} = 0.2$ ，调节微分和积分环节参数，最终得到的仿真数据如(a)所示, 为满足Hurwtiz条件，滑模面切换函数参数 ${c_1}$ 、 ${c_2}$ 均大于0，经过调整，得到具有较好控制效果的仿真数据，如(b)所示。在EHA的反演递推过程中，根据位移、速度和进油腔压力3个系统状态变量的整合，为满足李雅普诺夫条件产生了3个控制参数 $k_{1}$ 、 ${k_2}$ 、 ${k_3}$ ，通过调节参数发现： ${k_1}$ 主导系统增益的快慢， ${k_2}$ 为系统阻尼， ${k_3}$ 可以减小系统振荡。调整3个参数的数值，得到反演控制的EHA联合仿真结果，如图4(c)所示。

由图4可知，反演控制系统在2 s左右开始控制EHA减速，此时EHA运动位移约为45 mm，是目标值50 mm的90%。EHA在3 s左右运动到目标值50 mm稳定下来，减速及调整时间占总运行时间的33.3%，且无抖振、超调等现象。PID控制最终仿真数据中，PID控制系统在约1.8 s开始控制EHA减速，此时EHA运动位移约为40 mm，是目标值50 mm的80%。EHA在4 s左右运动到目标值50 mm稳定下来，减速及调整时间占总运行时间的55%，但易超调、调整时间长等有待改进的地方。滑模变结构控制最终仿真数据中，滑模变结构控制系统在1.9 s左右开始控制EHA减速，此时EHA运动位移约为43 mm，为目标值50 mm的86%。EHA在4.2 s左右运动到目标值50 mm稳定下来，减速及调整时间占总运行时间的54.7%，且EHA在3 s左右发生超调，有一定的抖振现象。仿真数据结果表明，EHA滑模变结构控制相比于经典PID控制没有控制效果的改善，且极易发生抖振现象。

将PID控制策略仿真结果中综合控制性能最好的一组仿真数据与滑模变结构控制策略仿真结果和反演控制仿真结果组合构成纵向对比原始数据组，如表4所示。

表 4 不同控制策略仿真数据

Table 4. Simulation data of different control strategies

控制策略	上升时间/s	控制精度/mm	最大超调量占比/%
PID控制	4.97	0.037	0.08
滑模变结构控制	2.74	0.642	1.28
反演控制	3.56	0.035	0.07

下载: 导出CSV

| 显示表格

仿真数据结果表明，从达到目标总用时长和开始减速调整时间占比来说，EHA反演控制在响应快速性及稳定性方面表现良好，有利于EHA的可靠控制。

4. EHA控制性能试验及分析

4.1 试验设备与方法

图5为钢轨打磨车EHA试验样机并装配对应的传感检测装置，样机在活塞杆缩回状态的长、宽、高分别为561，163，310 mm，不装载油液质量为18.8 kg。

图 5 钢轨打磨车专用EHA

Figure 5. Special EHA for rail grinding vehicle

下载: 全尺寸图片幻灯片

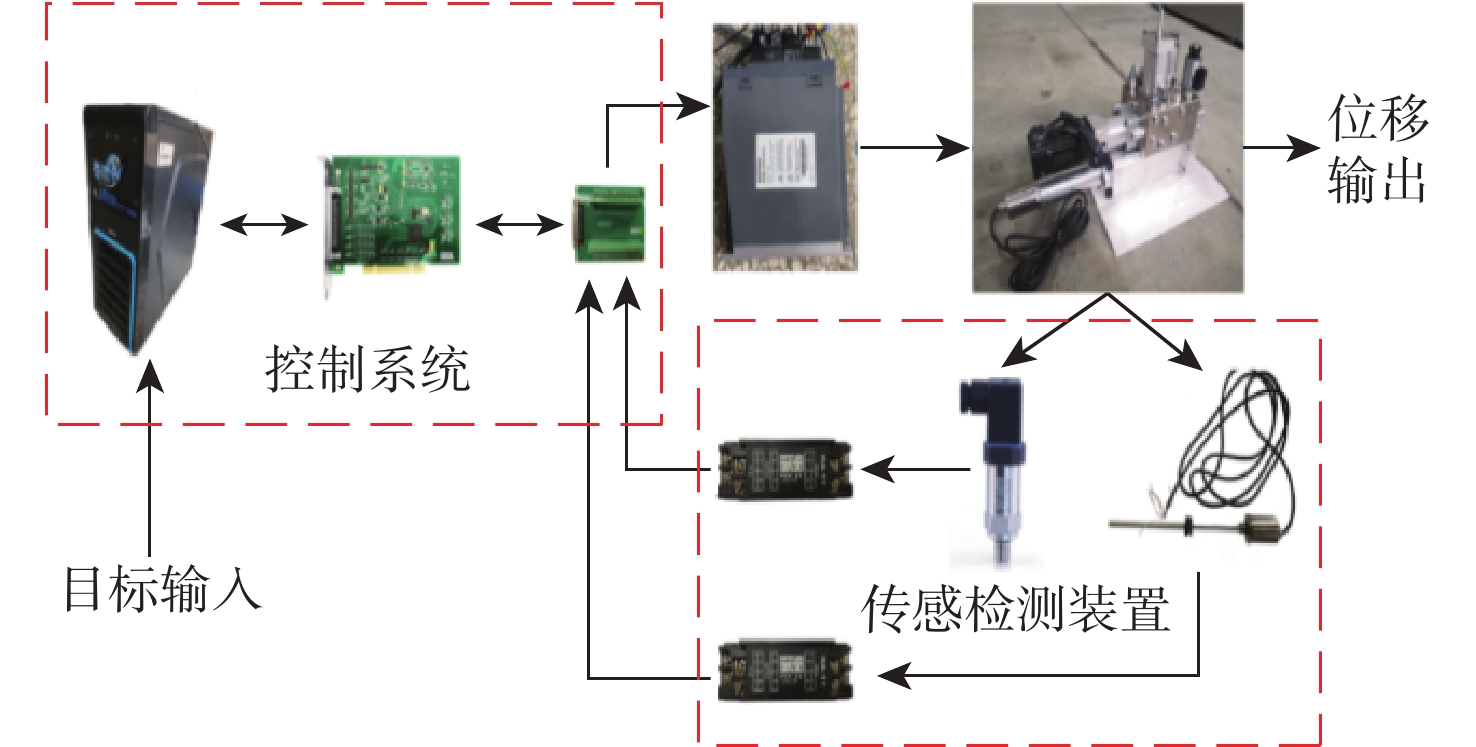
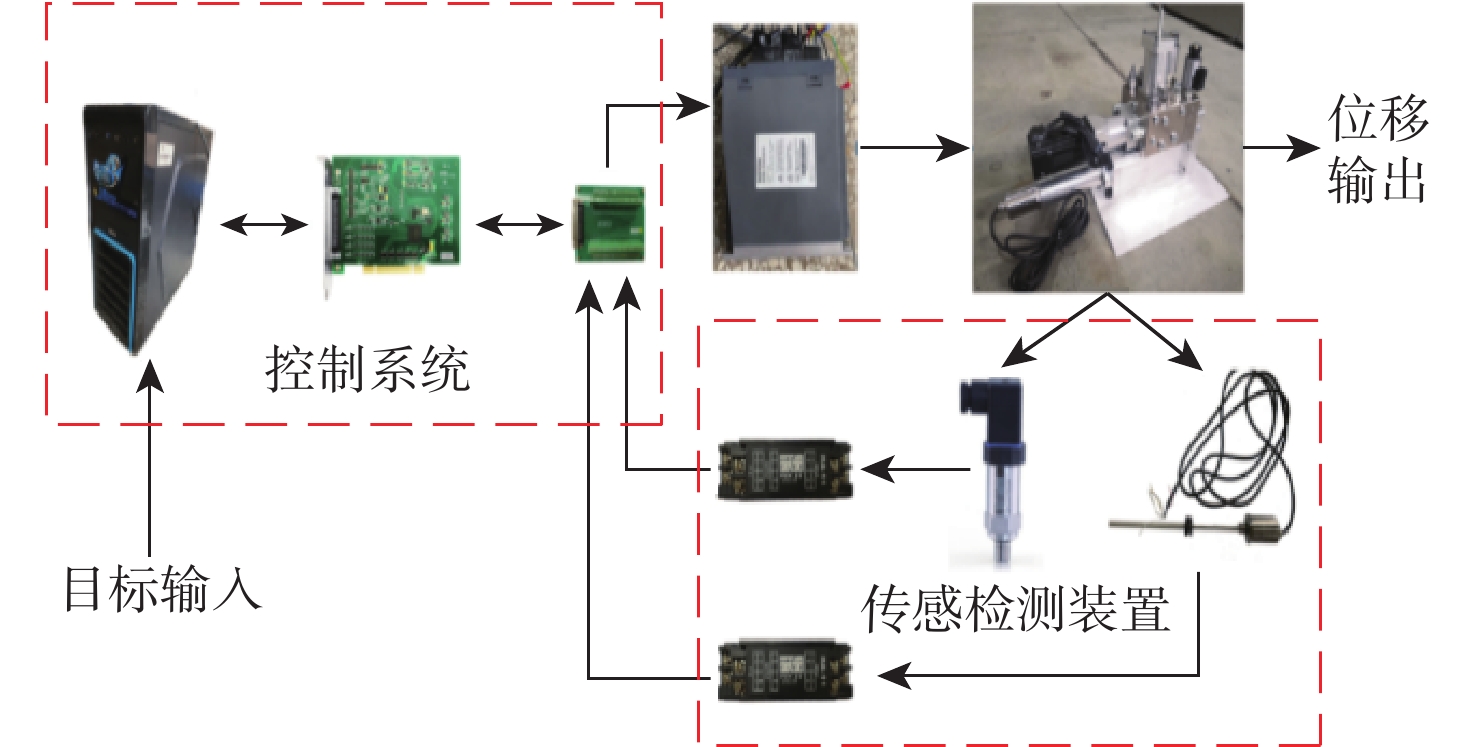
控制系统通过从Windows等上位机发送控制信号，经采集控制板卡和电机驱动器传递到EHA实现目标运动，并通过LVDT位移传感器和压力变送器反馈实时作动信号，隔离模块将信号转换之后由采集板卡采集回上位机进行控制策略的运算，形成控制闭环，EHA控制性能试验的流程图如图6所示。

图 6 EHA控制性能试验的流程图

Figure 6. Control performance test flow chart of EHA

下载: 全尺寸图片幻灯片

EHA控制性能试验的目的是通过不同的控制策略在EHA上的应用，对比在柱塞泵效率、液压缸摩擦力等非线性因素影响下的EHA可靠控制策略。根据EHA设计的背景领域及建立的评价体系，EHA控制性能试验评价EHA主要性能的关键参数是EHA的液压缸往复运动的响应快慢和位移精度2个指标。为真实地模拟还原EHA在实际应用中可能遇到的工况，得到各控制策略更准确的性能表现，EHA控制目标设定为其满行程的一半50 mm，且不设置外负载，将不同控制策略分组进行测试，测量EHA运动至目标值50 mm并稳定下来的时长及最后的稳定精度。利用四象限工况试验平台进行负载施加，对控制策略进行多种负载工况条件下，不同控制目标的控制性能测试，以验证其控制效果的优越性。

4.2 控制性能试验结果及分析

4.2.1 控制策略试验结果

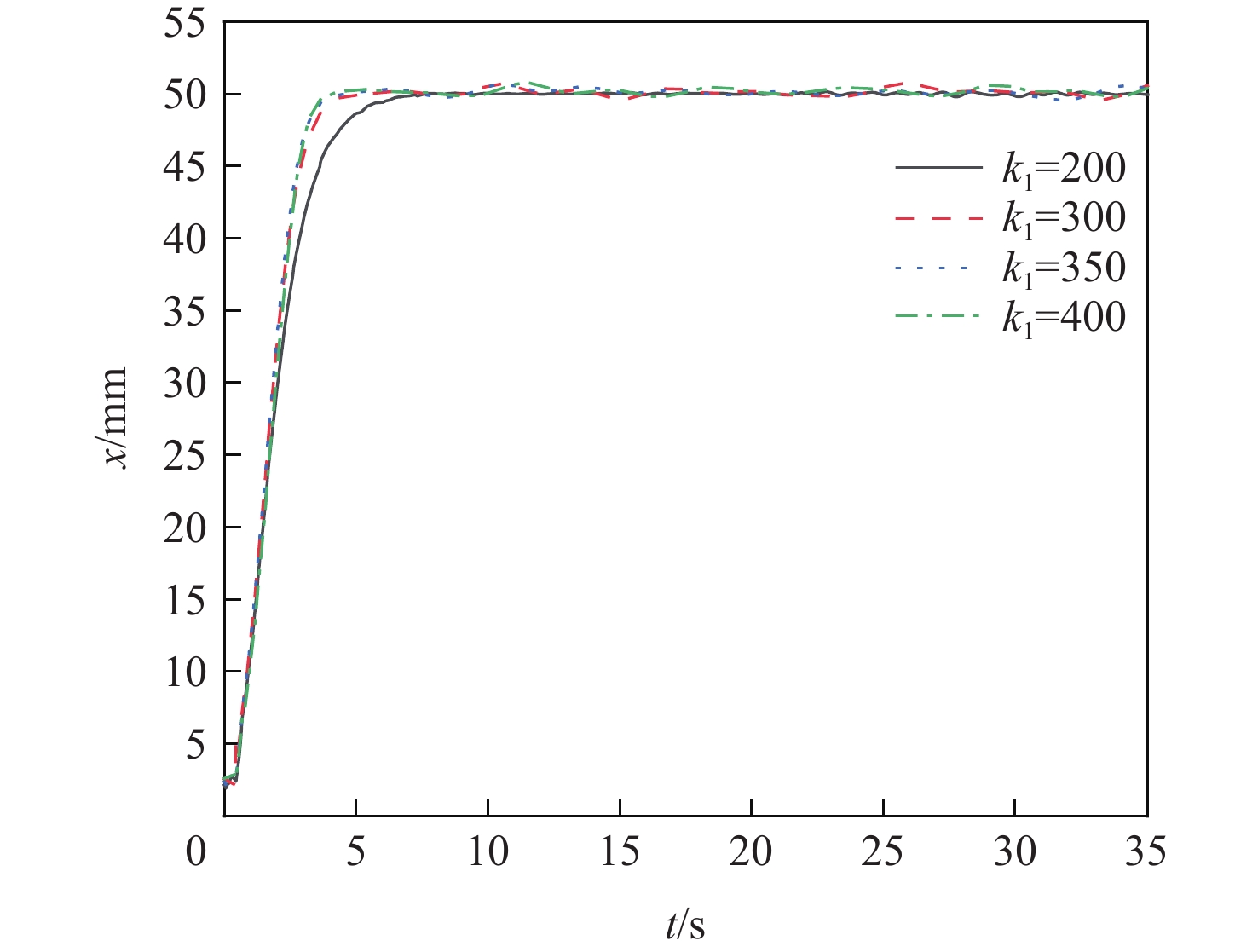
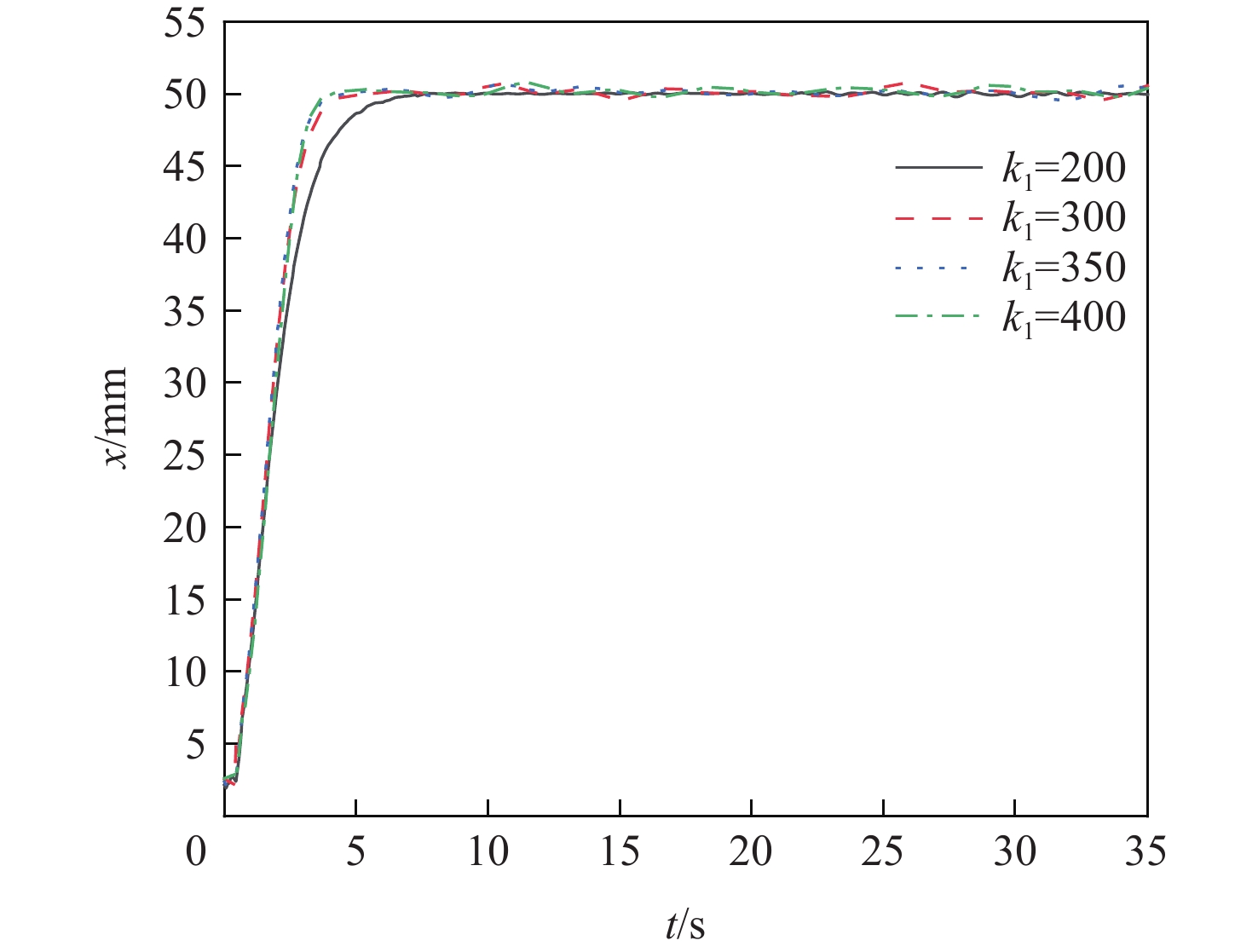
基于反演控制仿真结果，以为满足李雅普诺夫条件产生的控制参数 ${k_1}$ 为主要调节参数，多次试验得到4组反演控制的阶跃响应位移反馈数据，经过数据信号转换及噪声滤波处理的试验结果对比如图7所示。

图 7 反演控制样机试验结果

Figure 7. Test results of backstepping control prototype

下载: 全尺寸图片幻灯片

根据EHA设计的背景领域，EHA控制性能的关键参数是EHA的液压缸往复运动的响应快慢和位移精度2个指标，如所示，以EHA阶跃响应的上升时间和控制精度作为评价指标，反演控制性能试验中，参数 ${k_1} = 200$ 时，控制精度达到0.09 mm得到的试验结果具有较好的综合控制性能。

表 5 反演控制试验数据

Table 5. Backstepping control test data

反演代表参数	上升时间/s	控制精度/mm	最大超调量占比/%
${k}_{1}=200$	8.49	0.09	0.18
${k}_{1}=300$	5.54	0.72	1.43
${k}_{1}=350$	4.62	0.65	1.31
${k}_{1}=400$	4.12	0.77	1.54

下载: 导出CSV

| 显示表格

4.2.2 反演控制四象限负载试验

文献[21]将油缸所受负载力与运动速度分为4种工况，称为全象限工况。参考文献[22-23]，本文对钢轨打磨车专用EHA作动工况进行统计后，根据外负载力是否阻碍液压缸的伸出和缩回运动，可分为4种工况：当外负载力阻碍液压缸的伸出和缩回运动时对应一、三象限工况，当外负载力的方向与液压缸动作一致时为二、四象限工况。

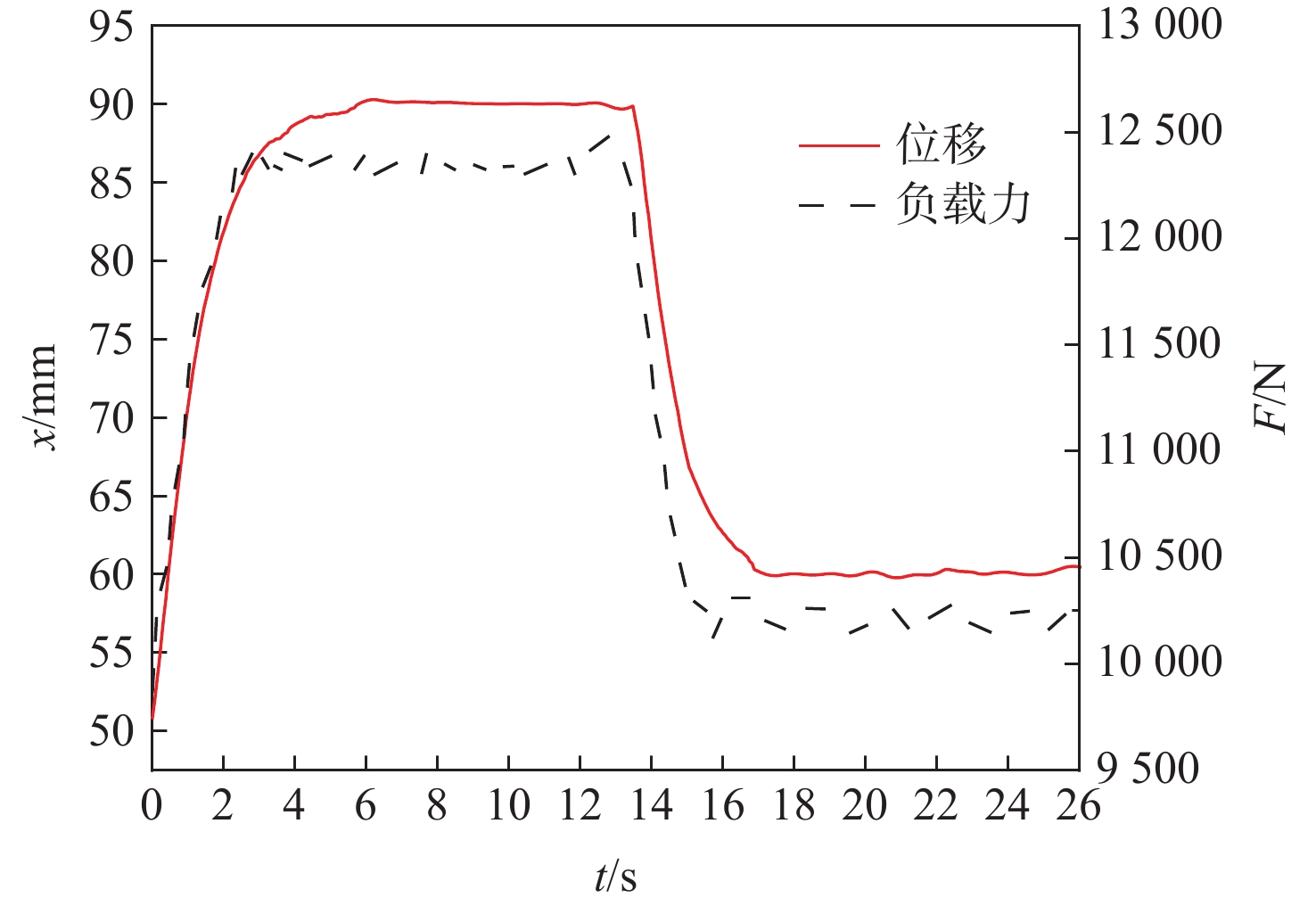
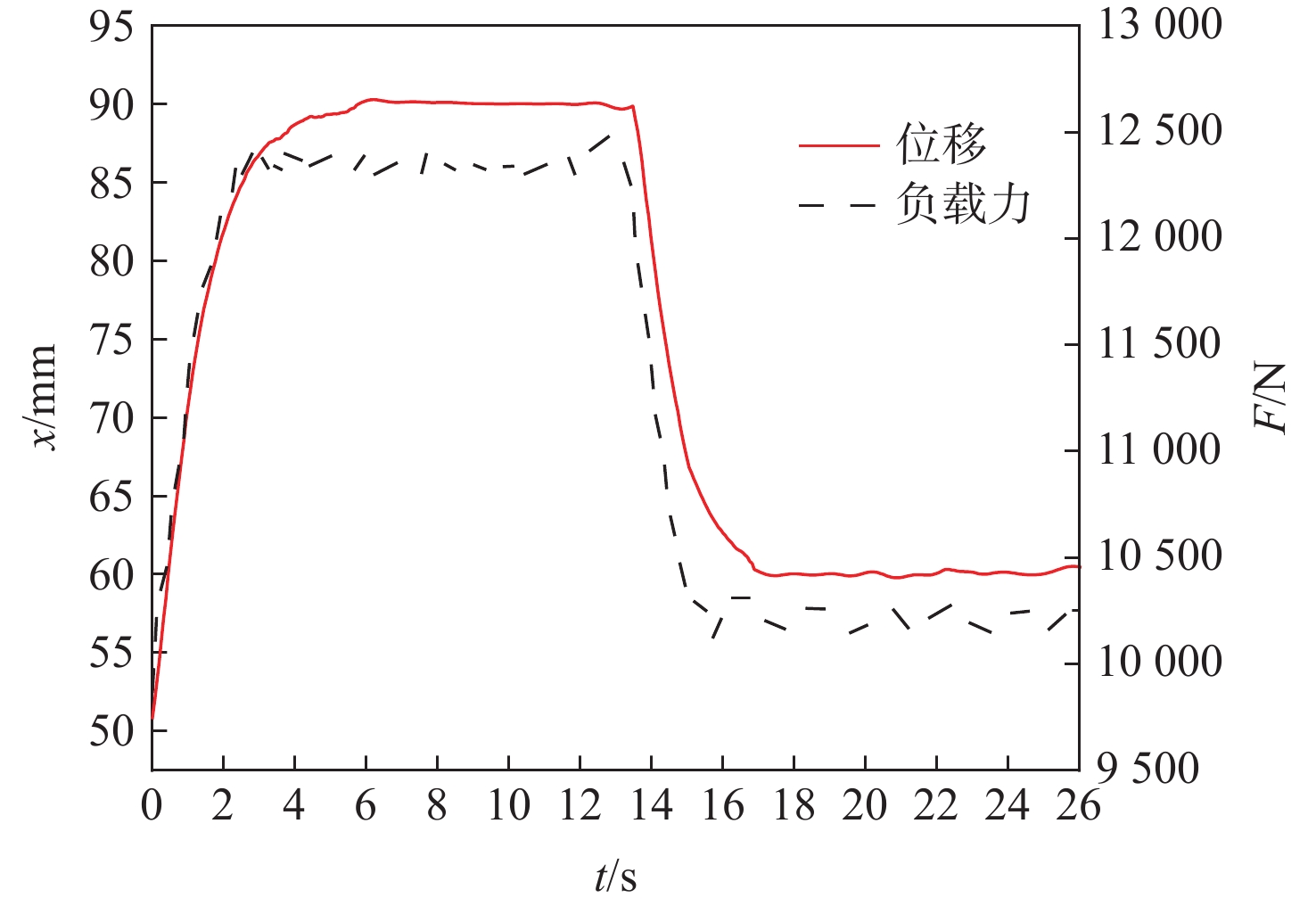
设计制作四象限试验台架，将其与EHA四象限试验平台组装，物理样机如图8所示。四象限试验平台设计时，以EHA位移行程中点等于50 mm为负载施加起点，考虑EHA运动至行程末端时受到机械结构限制，位移控制目标行程不满为优。因此，在正负载至负负载试验方案中，样机位移选择从50 mm处运动至90 mm处再回到60 mm处，在前40 mm行程中处于正负载工况，后30 mm行程处于负负载工况，试验结果如图9所示。

图 8 EHA四象限试验台架

Figure 8. Four quadrant test bench of EHA

下载: 全尺寸图片幻灯片

图 9 正负载至负负载样机试验

Figure 9. Prototype test from positive load to negative load

下载: 全尺寸图片幻灯片

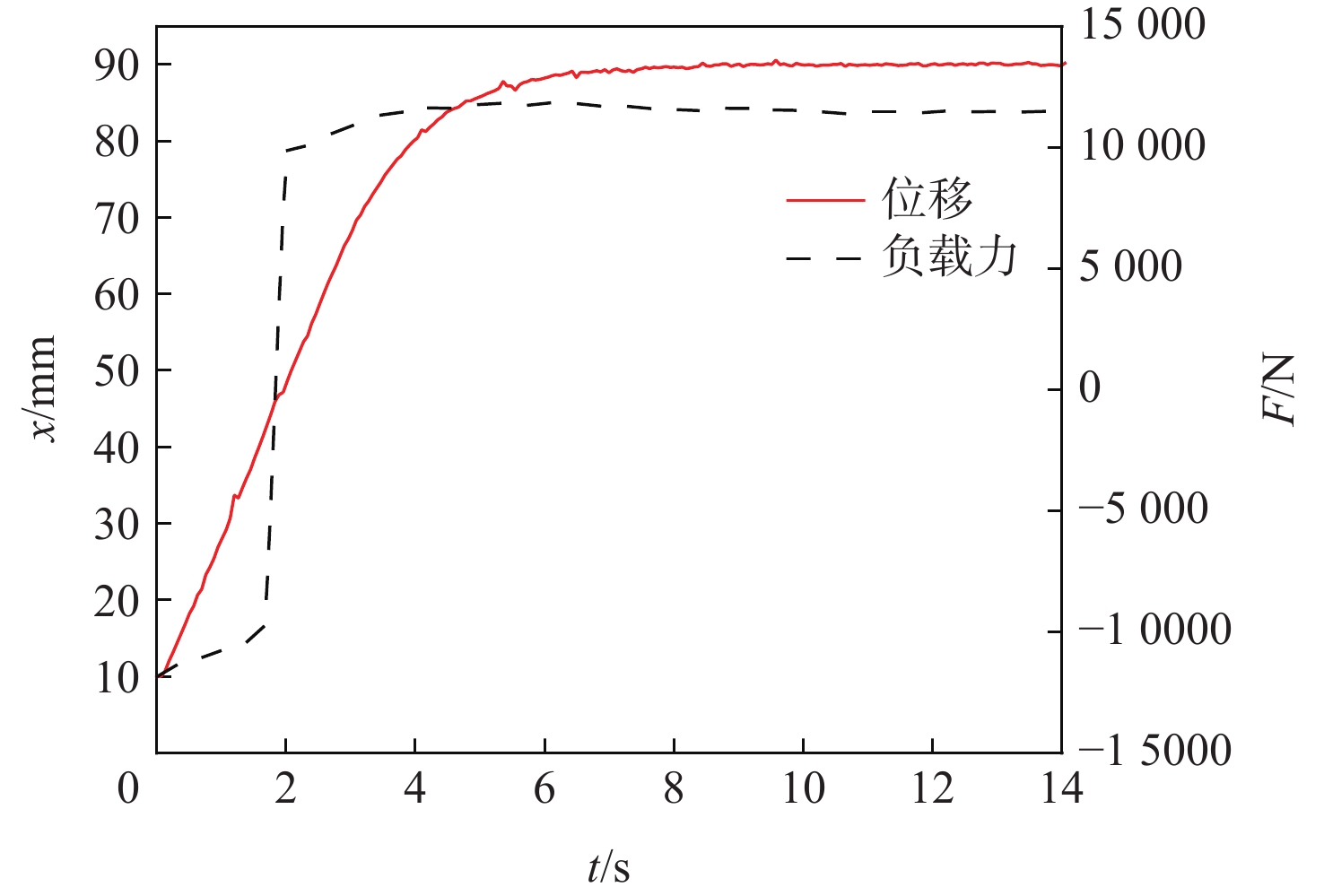
负负载至正负载试验方案中，样机位移由10 mm处运动至90 mm处，前40 mm行程处于负负载工况，后40 mm行程处于正负载工况，试验结果如图10所示。

图 10 负负载至正负载样机试验

Figure 10. Prototype test from negative load to positive load

下载: 全尺寸图片幻灯片

综合图9和图10这2种负载变化情况下的EHA样机反演控制试验结果，得出其控制精度最大误差约为0.21 mm。控制精度低于无负载情况下的反演控制效果，但在EHA限定的最大超调量范围内。四象限负载试验结果表明，反演控制在各负载施加情况下均具有可靠的控制效果。

5. 结　论

1）将钢轨打磨车打磨头角度的偏转和打磨电机的避障升降这2种作动的实现作为目标，设计钢轨打磨车专用EHA，建立了电机、液压系统数学模型，考虑泵的总效率波动和液压缸动静摩擦差异大2个非线性因素，建立了相应的非线性数学模型。

2）以EHA数学模型为基础，设计反演控制器，搭建AMEsim与Simulink联合仿真平台，验证了反演控制在响应快速性及稳定性方面表现良好，具有较好的控制性能。

3）试制EHA试验样机，在空载试验下得出控制参数 ${k_1} = 200$ 时具有较好的控制效果；设计四象限工况负载试验包架，对EHA进行四象限工况试验，反演控制策略的控制精度最大误差约为0.21 mm，低于空载试验效果，满足EHA控制目标。

相比美国雷萨EHA控制精度，本文所设计的EHA控制精度还不够理想，需进一步开展的工作包括：本文采用易于控制的泵控对称液压缸作为执行元件，流量不匹配的非对称缸控制效果需进一步探索；由于传感器精度、采集模式、控制系统软硬件等条件的限制，具有较强的干扰噪声，控制精度不够理想，可逐项针对矛盾进行改进优化。本文使用工控机加控制板卡的控制方式具有局限性，未来可采用嵌入式控制系统使EHA集成度更高，整机互换性更强，有利于应用领域的拓展。

图 1 专用EHA液压原理

Figure 1. Hydraulic principle of special EHA

下载: 全尺寸图片幻灯片

图 2 EHA的反演控制系统模型

Figure 2. Backstepping control system model of EHA

下载: 全尺寸图片幻灯片

图 3 EHA的联合仿真模型

Figure 3. Joint simulation model of EHA

下载: 全尺寸图片幻灯片

图 4 不同控制策略仿真结果

Figure 4. Simulation results of different control strategies

下载: 全尺寸图片幻灯片

图 5 钢轨打磨车专用EHA

Figure 5. Special EHA for rail grinding vehicle

下载: 全尺寸图片幻灯片

图 6 EHA控制性能试验的流程图

Figure 6. Control performance test flow chart of EHA

下载: 全尺寸图片幻灯片

图 7 反演控制样机试验结果

Figure 7. Test results of backstepping control prototype

下载: 全尺寸图片幻灯片

图 8 EHA四象限试验台架

Figure 8. Four quadrant test bench of EHA

下载: 全尺寸图片幻灯片

图 9 正负载至负负载样机试验

Figure 9. Prototype test from positive load to negative load

下载: 全尺寸图片幻灯片

图 10 负负载至正负载样机试验

Figure 10. Prototype test from negative load to positive load

下载: 全尺寸图片幻灯片

表 1 EHA设计指标

Table 1. Design indexes of EHA

行程/mm	负载力/KN	速度/（mm·s⁻¹）	位移全尺寸精度/%
100	≤10	≥20	≤0.77

下载: 导出CSV

表 2 摩擦模型相关参数

Table 2. Relevant parameters of friction model

${{{\sigma _0}} / ({{\mathrm{N}} \cdot {\mathrm{m}}}})$	${{{\sigma _1}} /( {{\mathrm{N}} \cdot {\mathrm{m}}}} \cdot {{\mathrm{s}}^{ - 1}})$	${{{\sigma _2}} /( {{\mathrm{N}} \cdot {\mathrm{m}} \cdot {{\mathrm{s}}^{ - 1}}}})$	${{{v_{\mathrm{s}}}} /({{\mathrm{N}} \cdot {\mathrm{m}} \cdot {{\mathrm{s}}^{ - 1}}}})$	${{ {{f_{\mathrm{c}}}} } /{{\mathrm{kN}}}}$	${{ {{f_{\mathrm{s}}}} }/ {{\mathrm{kN}}}}$
$2.1\times {10}^{7}$	0.1	150	0.1	142	12

下载: 导出CSV

表 3 EHA仿真参数

Table 3. Simulation parameters of EHA

参数	数值
油缸有效行程/mm	100
油缸直径/mm	63
活塞杆直径/mm	35
泵额定转速/（r·min⁻¹）	3000
泵排量/(ml·r⁻¹)	1
溢流压力/MPa	8
转子惯量/( $\mathrm{k}\mathrm{g}\cdot{{\mathrm{m}}}^{2}$ )	$2.7\times {10}^{-5}$
线电阻/Ω	5.5
线电感/H	$9.6\times {10}^{-3}$
反电势常数/( $\mathrm{V}\cdot \mathrm{m}\cdot {{\mathrm{r}}}^{-1}$ )	$3.2\times {10}^{-2}$

下载: 导出CSV

表 4 不同控制策略仿真数据

Table 4. Simulation data of different control strategies

控制策略	上升时间/s	控制精度/mm	最大超调量占比/%
PID控制	4.97	0.037	0.08
滑模变结构控制	2.74	0.642	1.28
反演控制	3.56	0.035	0.07

下载: 导出CSV

表 5 反演控制试验数据

Table 5. Backstepping control test data

反演代表参数	上升时间/s	控制精度/mm	最大超调量占比/%
${k}_{1}=200$	8.49	0.09	0.18
${k}_{1}=300$	5.54	0.72	1.43
${k}_{1}=350$	4.62	0.65	1.31
${k}_{1}=400$	4.12	0.77	1.54

下载: 导出CSV

参考文献(23)

[1]	铁道技术监督编辑部. 新时代交通强国铁路先行规划纲要[J]. 铁道技术监督, 2020, 48(9): 1-6. doi: 10.3969/j.issn.1006-9178.2020.09.001 Editorial Department of Railway Quality Control. Outline of powerful nation railway advance planning in the new era[J]. Railway Quality Control, 2020, 48(9): 1-6 (in Chinese). doi: 10.3969/j.issn.1006-9178.2020.09.001
[2]	SCHOCH W. Rail grinding strategies for achieving optimum results: An inventory[J]. Rail Engineering International, 2008, 37(1): 4-6.
[3]	李军. 钢轨打磨技术及其应用[J]. 铁路采购与物流, 2017, 12(3): 59-60. doi: 10.3969/j.issn.1673-7121.2017.03.015 LI J. Rail grinding technology and its application[J]. Railway Purchasing and Logistics, 2017, 12(3): 59-60 (in Chinese). doi: 10.3969/j.issn.1673-7121.2017.03.015
[4]	SATOH Y, IWAFUCHI K. Effect of rail grinding on rolling contact fatigue in railway rail used in conventional line in Japan[J]. Wear, 2008, 265(9-10): 1342-1348. doi: 10.1016/j.wear.2008.02.036
[5]	SROBA P, RONEY M. Rail grinding best practices[C]//Proceedings of the Annual Conference of the American Railway Engineering and Maintenance of Way Association. Chicago: IL, 2003: 1-41.
[6]	KALOUSEK J, SROBA P, MAGEL E. Shuswap subdivision rail samples metallographic examination of high and low rails from sharp curves[R]. Washington, D. C. : NRC, 2000.
[7]	熊志林, 陶建峰, 张峰榕, 等. 采用状态估计的泵控非对称液压缸模型预测控制[J]. 西安交通大学学报, 2017, 51(4): 109-115. XIONG Z L, TAO J F, ZHANG F R, et al. A model predictive control strategy of pump-controlled asymmetric cylinders using state estimation[J]. Journal of Xi’an Jiaotong University, 2017, 51(4): 109-115 (in Chinese).
[8]	纪铁铃, 齐海涛, 滕雅婷. 基于AMESim和MATLAB联合仿真的EHA滑模变结构控制分析[J]. 液压与气动, 2016(3): 19-24. doi: 10.11832/j.issn.1000-4858.2016.03.004 JI T L, QI H T, TENG Y T. Analysis of sliding-mode control for EHA based on AMESim and MATLAB co-simulation[J]. Chinese Hydraulics & Pneumatics, 2016(3): 19-24 (in Chinese). doi: 10.11832/j.issn.1000-4858.2016.03.004
[9]	付永领, 王利剑, 齐海涛, 等. 基于DSP和CPLD的电动静液作动器双余度控制器设计[J]. 测控技术, 2010, 29(1): 39-43. doi: 10.3969/j.issn.1000-8829.2010.01.013 FU Y L, WANG L J, QI H T, et al. Design of dual-redundancy control system for electro-hydrostatic actuator based on DSP and CPLD[J]. Measurement & Control Technology, 2010, 29(1): 39-43 (in Chinese). doi: 10.3969/j.issn.1000-8829.2010.01.013
[10]	张星晴, 段富海. 基于遗传算法的EHA调速系统设计与优化[J]. 计算机仿真, 2014, 31(8): 32-36. doi: 10.3969/j.issn.1006-9348.2014.08.008 ZHANG X Q, DUAN F H. Design and optimization of EHA speed control system based on genetic algorithm[J]. Computer Simulation, 2014, 31(8): 32-36 (in Chinese). doi: 10.3969/j.issn.1006-9348.2014.08.008
[11]	KOKOTOVIC P, ARCAK M. Constructive nonlinear control: Progress in the 90's[C]//Proceedings of the IFAC. Beijing: IFAC , 1999, 32(2): 49-77.
[12]	冯娜娜. 钢轨打磨设备及运用[M]. 成都: 西南交通大学出版社, 2017: 6-8. FENG N N. Rail grinding equipment and its application[M]. Chengdu: Southwest Jiaotong University Press, 2017: 6-8 (in Chinese).
[13]	舒志兵. 交流伺服运动控制系统[M]. 北京: 清华大学出版社, 2006: 20-33. SHU Z B. AC servo motion control system[M]. Beijing: Tsinghua University Press, 2006: 20-33 (in Chinese).
[14]	王春行. 液压控制系统[M]. 北京: 机械工业出版社, 2011: 60-65. WANG C X. Hydraulic control system[M]. Beijing: China Machine Press, 2011: 60-65(in Chinese).
[15]	付永领, 李祝锋, 祁晓野, 等. 轴向柱塞式电液泵能量转化效率研究[J]. 机械工程学报, 2014, 50(14): 204-212. doi: 10.3901/JME.2014.14.204 FU Y L, LI Z F, QI X Y, et al. Research on the energy conversion efficiency of axial piston electro-hydraulic pump[J]. Journal of Mechanical Engineering, 2014, 50(14): 204-212 (in Chinese). doi: 10.3901/JME.2014.14.204
[16]	王林鸿, 吴波, 杜润生, 等. 液压缸运动的非线性动态特征[J]. 机械工程学报, 2007, 43(12): 12-19. doi: 10.3321/j.issn:0577-6686.2007.12.003 WANG L H, WU B, DU R S, et al. Nonlinear dynamic characteristics of moving hydraulic cylinder[J]. Chinese Journal of Mechanical Engineering, 2007, 43(12): 12-19 (in Chinese). doi: 10.3321/j.issn:0577-6686.2007.12.003
[17]	CANUDAS DE WIT C, OLSSON H, ASTROM K J, et al. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419-425. doi: 10.1109/9.376053
[18]	ZHOU Z, ZHENG X D, WANG Q, et al. Modeling and simulation of point contact multibody system dynamics based on the 2D LuGre friction model[J]. Mechanism and Machine Theory, 2021, 158: 104244. doi: 10.1016/j.mechmachtheory.2021.104244
[19]	邹怀静, 王海波, 王鑫, 等. 高功率密度微型斜盘式柱塞泵虚拟样机仿真分析[J]. 机床与液压, 2022, 50(10): 148-153. doi: 10.3969/j.issn.1001-3881.2022.10.028 ZOU H J, WANG H B, WANG X, et al. Virtual prototype simulation analysis of high power density miniature axial piston pump[J]. Machine Tool & Hydraulics, 2022, 50(10): 148-153 (in Chinese). doi: 10.3969/j.issn.1001-3881.2022.10.028
[20]	何建海, 张建霞. 基于AMESim及MATLAB/Simulink联合仿真的风帆转角复合控制[J]. 机床与液压, 2022, 50(4): 140-145. doi: 10.3969/j.issn.1001-3881.2022.04.027 HE J H, ZHANG J X. Compound control of the sail angle based on AMESim-MATLAB/simulink co-simulation[J]. Machine Tool & Hydraulics, 2022, 50(4): 140-145 (in Chinese). doi: 10.3969/j.issn.1001-3881.2022.04.027
[21]	BUTT K, COSTA G K, SEPEHRI N. Optimization-driven controller design for a high-performance electro-hydrostatic asymmetric actuator operating in all quadrants[J]. Journal of Dynamic Systems, Measurement, and Control, 2021, 143(9): 094503. doi: 10.1115/1.4050722
[22]	ZOU H J, WANG H B, WANG X, et al. Research on electro-hydrostatic actuator for large scale operation and maintenance equipment of railway line[C]//Proceedings of the ICRT. Reston: American Society of Civil Engineers, 2022: 503-514.
[23]	王鑫, 王海波, 邹怀静. 非对称液压缸EHA专用流量匹配阀的设计与分析[J]. 机床与液压, 2022, 50(6): 65-70. doi: 10.3969/j.issn.1001-3881.2022.06.011 WANG X, WANG H B, ZOU H J. Design and analysis of EHA special flow matching valve for asymmetric hydraulic cylinder[J]. Machine Tool & Hydraulics, 2022, 50(6): 65-70 (in Chinese). doi: 10.3969/j.issn.1001-3881.2022.06.011

施引文献

资源附件(0)

访问统计

点击查看大图

图(10) / 表(5)

计量

文章访问数: 242
HTML全文浏览量: 121
PDF下载量: 7
被引次数: 0

1. EHA的数学模型
1.1 永磁同步电机与泵控缸模型
1.2 非线性参数理论建模
2. 反演控制器设计
3. 联合仿真
3.1 钢轨打磨车专用EHA仿真建模
3.2 控制策略仿真分析
4. EHA控制性能试验及分析
4.1 试验设备与方法
4.2 控制性能试验结果及分析
5. 结　论

1. EHA的数学模型
1.1 永磁同步电机与泵控缸模型
1.2 非线性参数理论建模
2. 反演控制器设计
3. 联合仿真
3.1 钢轨打磨车专用EHA仿真建模
3.2 控制策略仿真分析
4. EHA控制性能试验及分析
4.1 试验设备与方法
4.2 控制性能试验结果及分析
5. 结　论

参考文献(23)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

钢轨打磨车专用EHA非线性反演控制

doi: 10.13700/j.bh.1001-5965.2022.0681

通讯作者:
E-mail：haibowang@home.swjtu.edu.cn

计量

Nonlinear backstepping control of special EHA for rail grinding vehicles

Corresponding author: E-mail：haibowang@home.swjtu.edu.cn

1. EHA的数学模型

1.1 永磁同步电机与泵控缸模型

1.2 非线性参数理论建模

1.2.1 柱塞泵效率

1.2.2 液压缸摩擦力

2. 反演控制器设计

3. 联合仿真

3.1 钢轨打磨车专用EHA仿真建模

3.2 控制策略仿真分析

4. EHA控制性能试验及分析

4.1 试验设备与方法

4.2 控制性能试验结果及分析

4.2.1 控制策略试验结果

4.2.2 反演控制四象限负载试验

5. 结　论

计量

目录

1. EHA的数学模型

1.1 永磁同步电机与泵控缸模型

1.2 非线性参数理论建模

2. 反演控制器设计

3. 联合仿真

3.1 钢轨打磨车专用EHA仿真建模

3.2 控制策略仿真分析

4. EHA控制性能试验及分析

4.1 试验设备与方法

4.2 控制性能试验结果及分析

5. 结　论

留言板

钢轨打磨车专用EHA非线性反演控制

doi: 10.13700/j.bh.1001-5965.2022.0681

通讯作者: E-mail：haibowang@home.swjtu.edu.cn

计量

出版历程

Nonlinear backstepping control of special EHA for rail grinding vehicles

Corresponding author: E-mail：haibowang@home.swjtu.edu.cn

1. EHA的数学模型

1.1 永磁同步电机与泵控缸模型

1.2 非线性参数理论建模

1.2.1 柱塞泵效率

1.2.2 液压缸摩擦力

2. 反演控制器设计

3. 联合仿真

3.1 钢轨打磨车专用EHA仿真建模

3.2 控制策略仿真分析

4. EHA控制性能试验及分析

4.1 试验设备与方法

4.2 控制性能试验结果及分析

4.2.1 控制策略试验结果

4.2.2 反演控制四象限负载试验

5. 结 论

计量

出版历程

目录

1. EHA的数学模型

1.1 永磁同步电机与泵控缸模型

1.2 非线性参数理论建模

2. 反演控制器设计

3. 联合仿真

3.1 钢轨打磨车专用EHA仿真建模

3.2 控制策略仿真分析

4. EHA控制性能试验及分析

4.1 试验设备与方法

4.2 控制性能试验结果及分析

5. 结 论

通讯作者:
E-mail：haibowang@home.swjtu.edu.cn

5. 结　论

5. 结　论