Multi-objective Harris Hawk optimization algorithm based on adaptive Gaussian mutation
-
摘要:
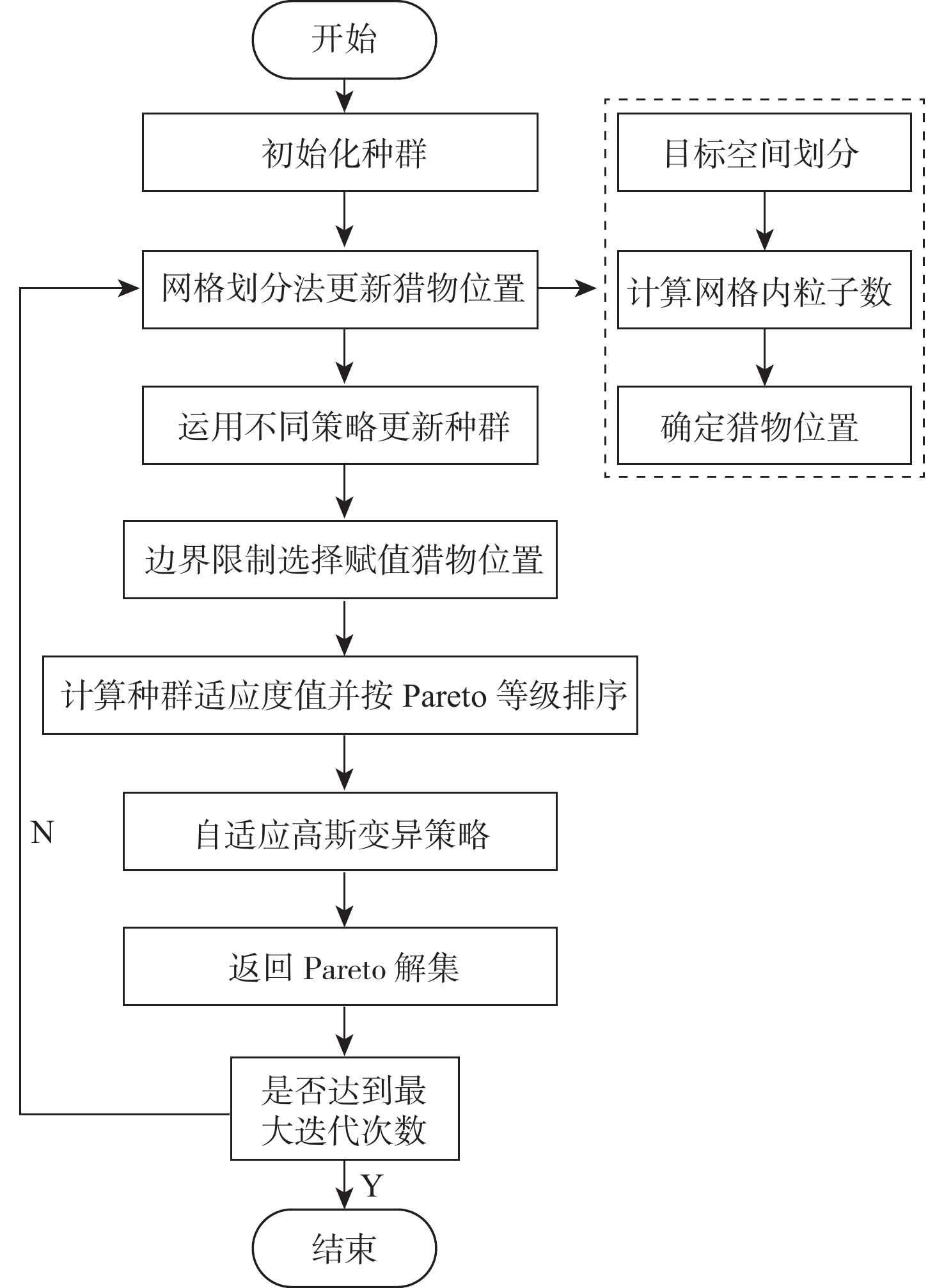
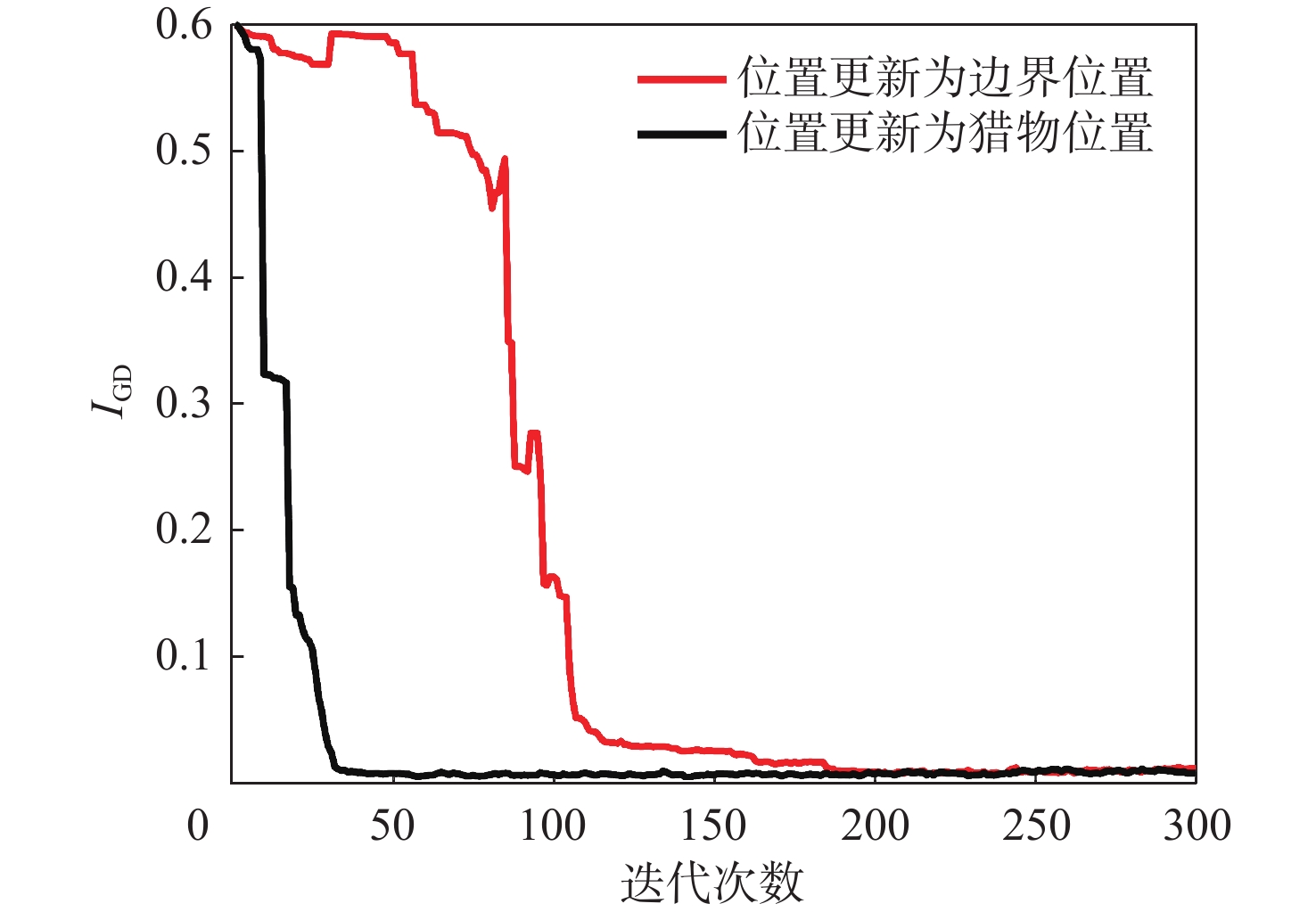
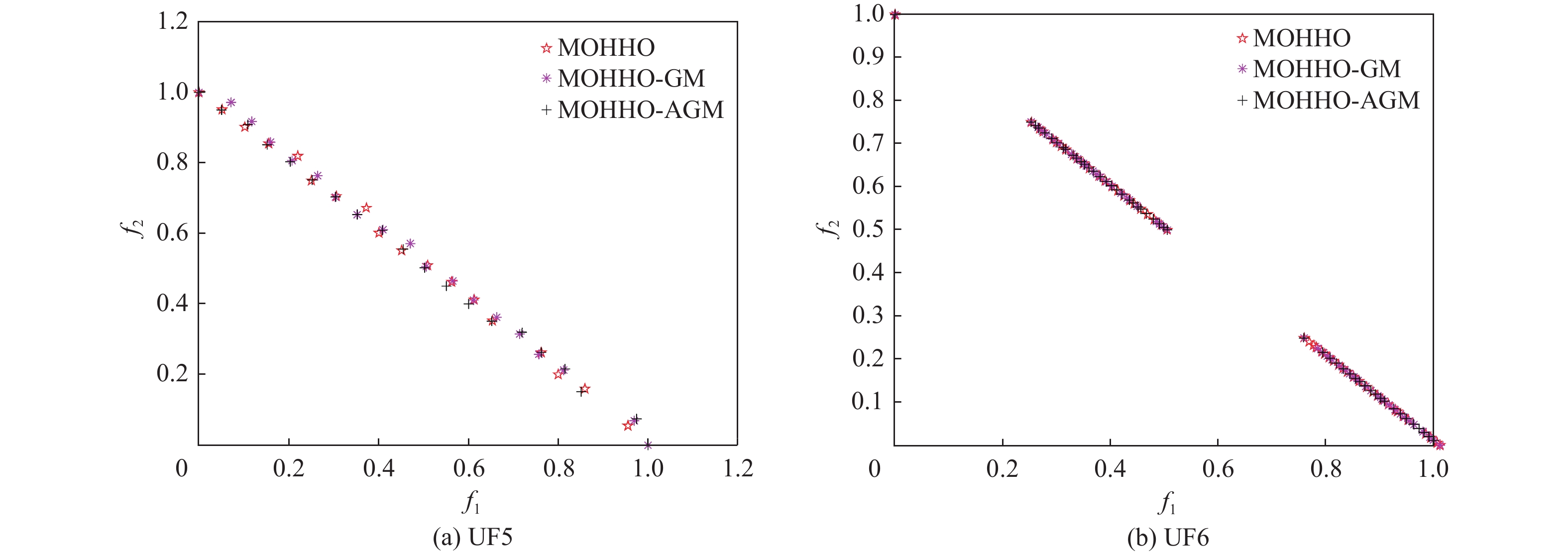
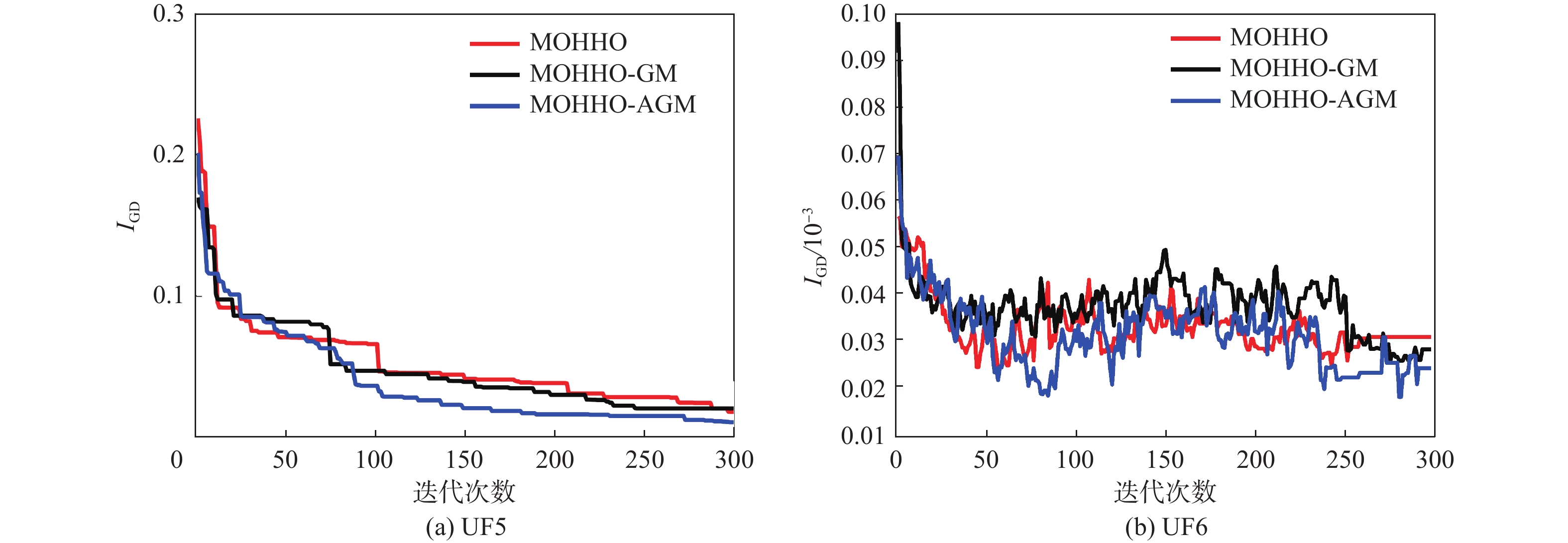
针对哈里斯鹰优化算法在求解多目标优化问题时种群多样性差导致算法容易陷入局部最优的问题，提出一种基于自适应高斯变异的多目标哈里斯鹰优化算法。为使解决方案更好地向Pareto前沿收缩，提出基于网格划分法的猎物位置定位方法；为提升算法收敛性能，将超出区间的种群个体位置更新为猎物位置；采用自适应高斯变异策略提高算法多样性和Pareto前沿种群粒子的均匀性。仿真结果表明：所提算法在求解多目标优化问题时，与多目标遗传算法(NSGA-Ⅱ)、多目标粒子群算法(MOPSO)、多目标灰狼算法(MOGWO)和多目标哈里斯鹰优化算法(MOHHO)比较，寻优精度增加了8.02%～51.34%，收敛速度增加了16.67%～40.74%，显著提升了所提算法的收敛速度和精度。
Abstract:The Harris Hawk optimization algorithm tends to fall into local optimum due to poor population diversity when solving multi-objective optimization problems. To address this issue, a multi-objective Harris Hawk optimization algorithm based on adaptive Gaussian mutation was proposed. To make the solution shrink to the Pareto frontier better, a prey location method based on the grid division method was proposed. To improve the convergence performance of the algorithm, the individual location of the population beyond the interval was updated to the prey location. An adaptive Gaussian mutation strategy was used to improve the algorithm diversity and the uniformity of the Pareto frontier population particles. The simulation results show that when the algorithm solves the multi-objective optimization problem, compared with multi-objective genetic algorithm (NSGA-Ⅱ), multi-objective particle swarm optimization (MOPSO), multi-objective gray wolf optimization (MOGWO), and multi-objective Harris Hawk optimization (MOHHO), the optimization accuracy is improved by 8.02%～51.34%, and the convergence speed is improved by 16.67%～40.74%. The research work provides new methods and technical means for solving multi-objective optimization problems.
-
图 2 不同位置更新方法的算法收敛速度对比
Figure 2. Comparison of algorithm convergence speed of different position update methods
图 3 不同算法在测试函数ZDT3、ZDT4上的分布情况
Figure 3. Distribution of different algorithms on test functions ZDT3 and ZDT4
图 4 不同算法在测试函数ZDT3、ZDT4上的收敛情况
Figure 4. Convergence of different algorithms on test functions ZDT3 and ZDT4
图 5 粒子超出边界时采取不同位置更新方法在ZDT4上的收敛情况
Figure 5. Convergence of different position update methods on ZDT4 when particles exceed the boundary
图 6 运用不同策略的MOHHO改进算法在UF5、UF6上的分布情况
Figure 6. The distribution of MOHHO improved algorithm using different strategies on UF5 and UF6
图 7 运用不同策略的MOHHO改进算法在UF5、UF6上的收敛情况
Figure 7. The convergence of MOHHO improved algorithms using different strategies on UF5 and UF6
表 1 局部开发阶段位置更新策略
Table 1. Location update strategy in local development stage
策略 位置更新 条件 软围攻 $ {\boldsymbol{X}}(t + 1) =\Delta {\boldsymbol{X}}(t) - E|J{{\boldsymbol{X}}_{{\text{rab}}}}(t) - {\boldsymbol{X}}(t)| $ $ r \geqslant 0.5, |E| \geqslant 0.5 $ 硬围攻 $ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{{\text{rab}}}}(t) - E|\Delta {\boldsymbol{X}}(t)|$ $ r \geqslant 0.5, |E| < 0.5 $ 渐进式快速
俯冲软包围$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{{\text{rab}}}}(t) - E|J{{\boldsymbol{X}}_{{\text{rab}}}}(t) - {\boldsymbol{X}}(t)| $
$ {\boldsymbol{Z}} = {\boldsymbol{Y }}+ {\boldsymbol{S}} \times {\mathrm{LF}}(D) $
$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {\boldsymbol{Y}}\quad\quad F{\text{(}}{\boldsymbol{Y}}{\text{) < }}F{\text{(}}{\boldsymbol{X}}{\text{(}}t{\text{))}} \\ {\boldsymbol{Z}}\quad\quad F{\text{(}}{\boldsymbol{Z}}{\text{) < }}F{\text{(}}{\boldsymbol{X}}{\text{(}}t{\text{))}} \\ \end{gathered} \right. $$ r < 0.5, |E| \geqslant 0.5 $ 渐进式快速
俯冲硬包围$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{{\text{rab}}}}(t) - E|J{{\boldsymbol{X}}_{{\text{rab}}}}(t) - {{\boldsymbol{X}}_{\text{m}}}(t)| $
$ {\boldsymbol{Z}} = {\boldsymbol{Y}} + {\boldsymbol{S}} \times {\mathrm{LF}}(D) $
$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {\boldsymbol{Y}}\quad\quad F({\boldsymbol{Y}}{\text{) < }}F{\text{(}}{\boldsymbol{X}}{{(t))}} \\ {\boldsymbol{Z}}\quad\quad F{\text{(}}{\boldsymbol{Z}}{\text{) < }}F{\text{(}}{\boldsymbol{X}}{{(t))}} \\ \end{gathered} \right. $$ r < 0.5, |E| < 0.5 $ 注：$ \Delta {\boldsymbol{X}}(t) $为第$ t $次迭代时哈里斯鹰与猎物之间的距离；$ J $为猎物逃逸时随机跳跃的距离；$ D $为问题维度；$ {\mathrm{LF}}(D) $为利用Levy函数(LF)[14]模拟猎物的逃逸行为；$ {\boldsymbol{S}} $为$D $的随机向量。 
下载: 导出CSV
表 2 算法参数设置
Table 2. Algorithm parameter setting
算法 参数设置 NSGA-Ⅱ 交叉率$ {P_{\mathrm{c}}} = 0.8 $、变异率$ {P_{\mathrm{m}}} = 0.1 $、突变概率$ \mu = 0.2 $、
突变步长$ \sigma = 0.1 \times ({b_{\text{u}}} - {b_{\text{l}}}) $MOPSO 权重$ w = 0.5 $、学习因子$ {c_1} = 1.5、{c_2} = 1.5 $ MOGWO $ {a}_{\mathrm{max}}=2、{a}_{\mathrm{min}}=0 $ MOHHO $ {E_0} \in [ - 1,1] $、$ {E_1} \in [0,2] $ MOHHO-GM $ {E_0} \in [ - 1,1] $、$ {E_1} \in [0,2] $、变异率$ M_{\mathrm{P}} = 0.1 $、
利用率$ E_{\mathrm{P}} = 0.5 $MOHHO-AGM $ {E_0} \in [ - 1,1] $、$ {E_1} \in [0,2] $、变异率$ M_{\mathrm{P}} = 0.1 $、
利用率$ E_{\mathrm{P}} = 0.5 $
下载: 导出CSV
表 3 标准测试函数
Table 3. Standard test functions
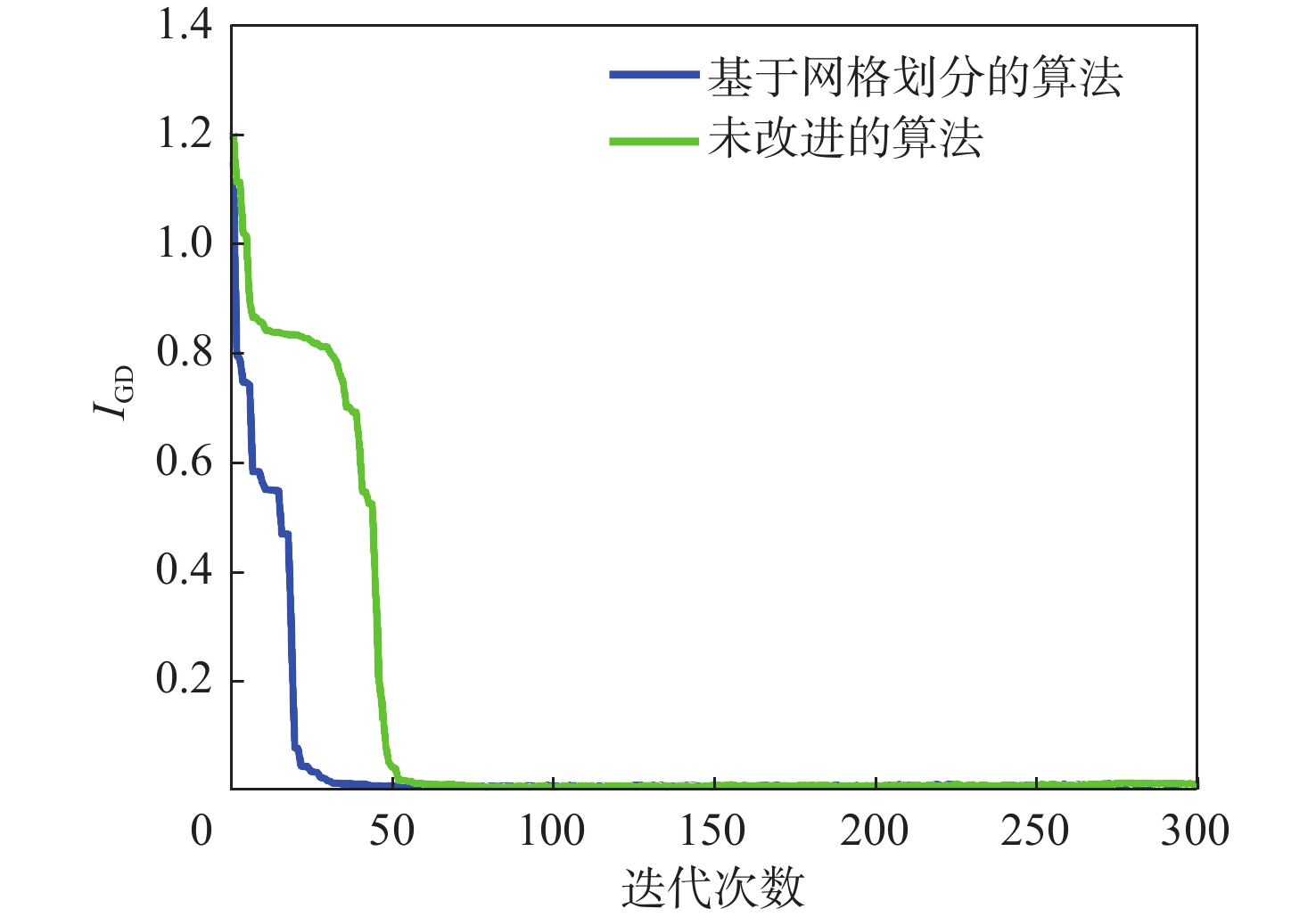
名称 目标函数个数 说明 名称 目标函数个数 说明 ZDT1 2 凸，连续 UF3 2 凸，连续 ZDT2 2 凹，连续 UF5 2 不连续 ZDT3 2 凹，不连续 UF6 2 不连续 ZDT4 2 凸，连续
下载: 导出CSV
表 4 运用网格划分法前后算法对比
Table 4. Comparison of algorithms before and after grid division
测试
函数平均值 标准差 未改进算法 基于网格
划分法算法未改进
算法基于网格
划分法算法ZDT1 8.76×10−3 6.30×10−3 0.82×10−3 0.48×10−3 UF6 3.27×10−3 3.03×10−3 0.58×10−3 0.30×10−3
下载: 导出CSV
表 5 不同变异策略算法的性能对比
Table 5. Performance comparison of different mutation strategy algorithms
测试
函数平均值 标准差 未应用
变异策略基于高斯
变异策略自适应
变异策略未应用
变异策略基于高斯
变异策略自适应
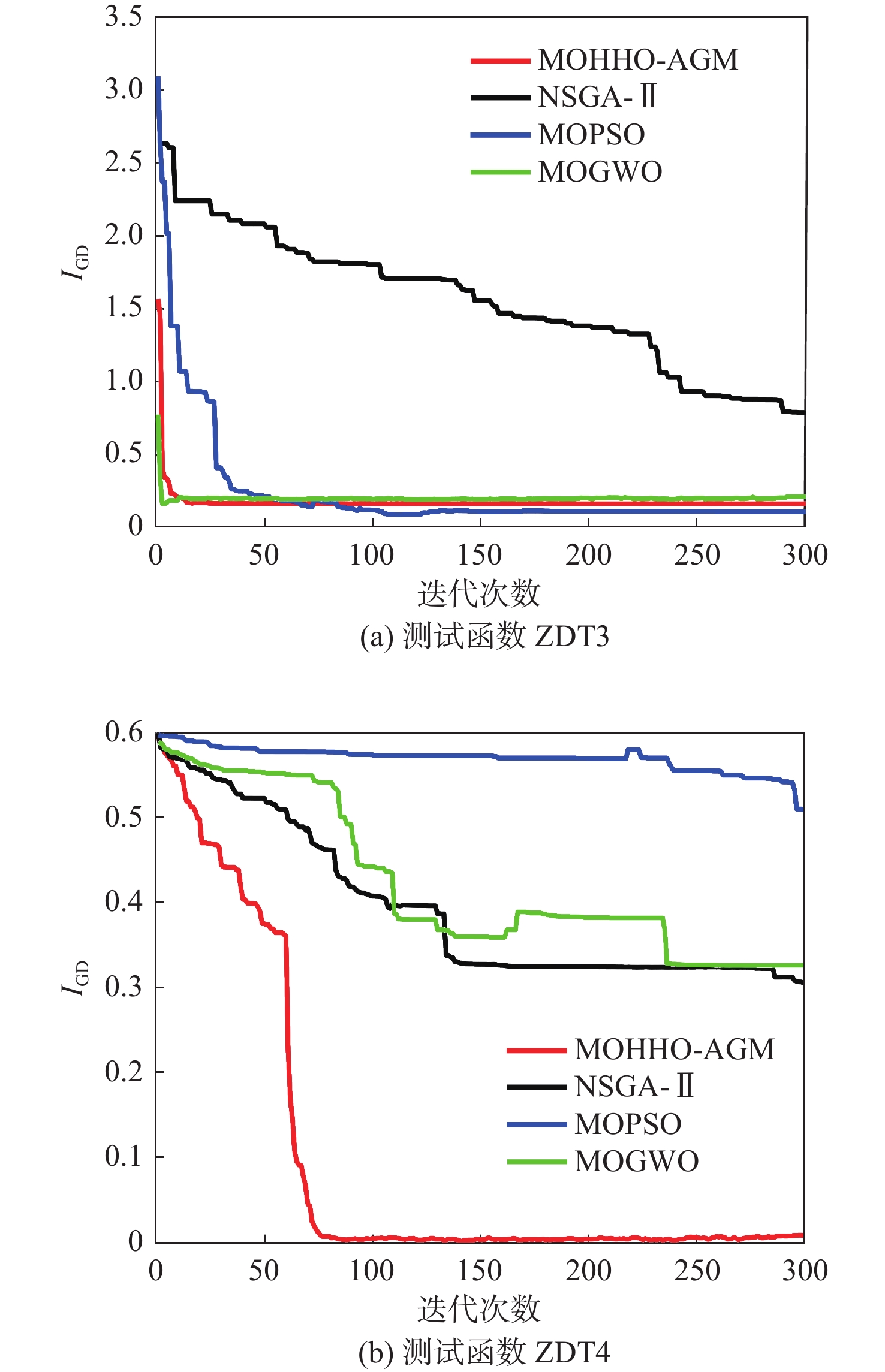
变异策略ZDT1 9.27×10−3 8.42×10−3 7.56×10−3 6.40×10−3 0.53×10−3 0.39×10−3 UF6 3.38×10−3 3.15×10−3 2.95×10−3 0.41×10−3 0.30×10−3 0.26×10−3
下载: 导出CSV
表 6 IGD测试结果
Table 6. Test results of IGD
测试
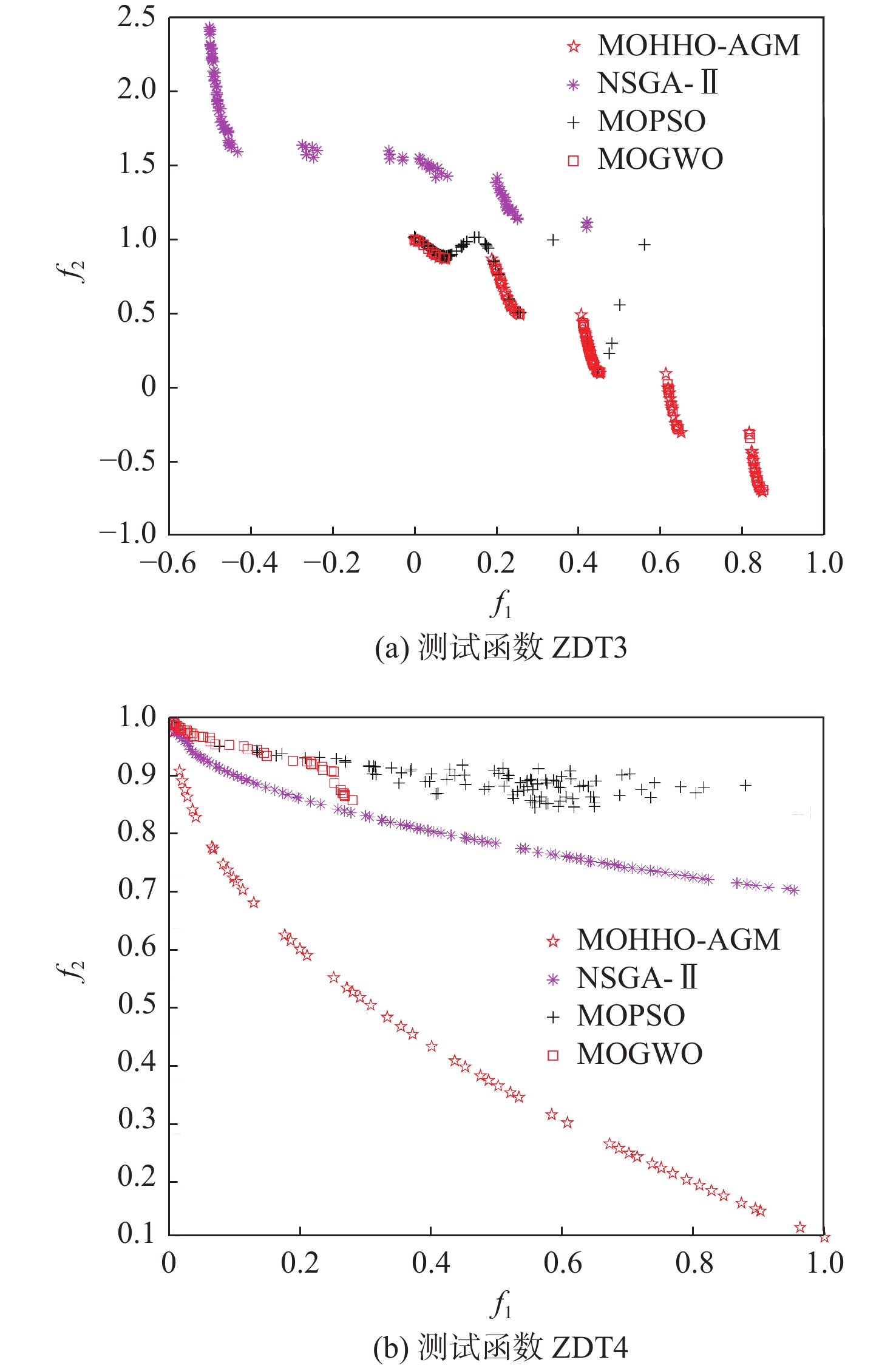
函数算法 最优值 平均值 最差值 标准差 等级 ZDT1 NSGA-Ⅱ 2.89×10−1 4.13×10−1 4.56×10−1 4.07×10−3 6 MOPSO 7.98×10−3 9.10×10−3 1.65×10−2 3.17×10−3 3 MOGWO 1.02×10−2 1.72×10−2 2.10×10−2 8.67×10−2 5 MOHHO 9.67×10−3 9.12×10−3 1.08×10−2 2.61×10−1 4 MOHHO-GM 7.68×10−3 8.51×10−3 9.71×10−3 7.10×10−4 2 MOHHO-AGM 7.55×10−3 8.37×10−3 9.22×10−3 6.36×10−4 1 ZDT2 NSGA-Ⅱ 1.78×10-0 2.31×10-0 2.87×10-0 3.51×10−1 6 MOPSO 1.01×10−2 1.29×10-0 2.14×10-0 7.20×10−1 5 MOGWO 1.50×10−2 5.06×10−1 1.94×10-0 7.54×10−1 4 MOHHO 8.90×10−3 4.79×10−1 6.13×10−1 2.66×10−1 3 MOHHO-GM 7.35×10−3 3.80×10−1 6.13×10−1 3.12×10−1 2 MOHHO-AGM 7.16×10−3 2.50×10−1 6.13×10−1 3.12×10−1 1 ZDT3 NSGA-Ⅱ 7.02×10−1 8.84×10−1 1.20×10-0 2.04×10−1 6 MOPSO 1.21×10−1 2.76×10−1 1.40×10-0 3.93×10−1 3 MOGWO 1.24×10−1 1.30×10−1 1.34×10−1 5.02×10−3 1 MOHHO 1.80×10−1 4.89×10−1 8.51×10−1 2.98×10−1 5 MOHHO-GM 1.80×10−1 2.92×10−1 8.51×10−1 2.73×10−1 4 MOHHO-AGM 1.79×10−1 2.40×10−1 7.20×10−1 1.80×10−1 2 ZDT4 NSGA-Ⅱ 2.66×10−1 3.20×10−1 3.95×10−1 4.85×10−2 4 MOPSO 3.77×10−1 5.06×10−1 5.51×10−1 5.56×10−2 6 MOGWO 3.28×10−1 4.89×10−1 5.88×10−1 7.77×10−1 5 MOHHO 6.26×10−3 8.54×10−3 1.16×10−2 1.72×10−3 2 MOHHO-GM 7.97×10−3 9.66×10−3 1.06×10−2 1.03×10−3 3 MOHHO-AGM 6.14×10−3 8.08×10−3 9.93×10−3 9.87×10−4 1 UF3 NSGA-Ⅱ 7.54×10−3 1.30×10−2 2.10×10−2 5.45×10−3 5 MOPSO 44.07×10−3 8.47×10−3 1.20×10−2 3.43×10−3 4 MOGWO 6.94×10−3 1.43×10−2 2.38×10−2 6.35×10−3 6 MOHHO 7.32×10−3 7.32×10−3 9.42×10−3 1.43×10−3 3 MOHHO-GM 6.04×10−3 7.45×10−3 8.07×10−3 1.42×10−3 2 MOHHO-AGM 4.71×10−3 6.05×10−3 7.21×10−3 9.04×10−4 1 UF5 NSGA-Ⅱ 1.82×10−3 3.78×10−2 5.61×10−2 1.56×10−2 6 MOPSO 5.64×10−2 7.25×10−2 7.42×10−2 1.41×10−2 5 MOGWO 1.29×10−2 1.26×10−2 1.85×10−2 5.17×10−2 1 MOHHO 1.34×10−2 1.90×10−2 2.41×10−2 4.18×10−3 4 MOHHO-GM 1.31×10−2 1.84×10−2 2.21×10−2 3.46×10−3 3 MOHHO-AGM 1.11×10−2 1.63×10−2 1.99×10−2 3.41×10−3 2 UF6 NSGA-Ⅱ 5.11×10−3 6.35×10−3 7.72×10−3 1.26×10−3 5 MOPSO 5.50×10−3 6.30×10−3 7.12×10−3 7.41×10−4 4 MOGWO 1.63×10−2 1.68×10−2 1.74×10−2 5.33×10−4 6 MOHHO 3.14×10−3 3.57×10−3 4.01×10−3 3.81×10−4 3 MOHHO-GM 2.89×10−3 3.53×10−3 4.36×10−3 4.74×10−4 2 MOHHO-AGM 2.48×10−3 3.28×10−3 3.86×10−3 3.94×10−4 1
下载: 导出CSV
-
[1] XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [2] LI S M, CHEN H L, WANG M J, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future Generation Computer Systems, 2020, 111: 300-323. doi: 10.1016/j.future.2020.03.055 [3] FARAMARZI A, HEIDARINEJAD M, MIRJALILI S, et al. Marine predators algorithm: a nature-inspired metaheuristic[J]. Expert Syst Appl, 2020, 152: 113377. doi: 10.1016/j.eswa.2020.113377 [4] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris Hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872. doi: 10.1016/j.future.2019.02.028 [5] SELIM A, KAMEL S, ALGHAMDI A S, et al. Optimal placement of DGs in distribution system using an improved Harris Hawks optimizer based on single- and multi-objective approaches[J]. IEEE Access, 2020, 8: 52815-52829. doi: 10.1109/ACCESS.2020.2980245 [6] MENESY A S, SULTAN H M, SELIM A, et al. Developing and applying chaotic Harris Hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks[J]. IEEE Access, 2020, 8: 1146-1159. [7] CHEN H L, JIAO S, WANG M J, et al. Parameters identification of photovoltaic cells and modules using diversification-enriched Harris Hawks optimization with chaotic drifts[J]. Journal of Cleaner Production, 2020, 244: 118778. doi: 10.1016/j.jclepro.2019.118778 [8] HOSSAIN M A, NOOR R M, YAU K L A, et al. Multi-objective Harris Hawks optimization algorithm based 2-hop routing algorithm for CR-VANET[J]. IEEE Access, 2021, 9: 58230-58242. [9] DU P, WANG J Z, HAO Y, et al. A novel hybrid model based on multi-objective Harris Hawks optimization algorithm for daily PM2.5 and PM10 forecasting[J]. Applied Soft Computing, 2020, 96: 106620. doi: 10.1016/j.asoc.2020.106620 [10] 蔡雪冰. 毫米波网络中用户多关联和下行功率分配的联合优化研究[D]. 温州: 温州大学, 2021.CAI X B. Joint optimal multi-connectivity enabled user association and power allocation in mmwave networks[D]. Wenzhou: Wenzhou University, 2021 (in Chinese). [11] 杜沛. 空气污染物浓度混合预测模型的研究及其在健康经济效益评估中的应用[D]. 大连: 东北财经大学, 2021.DU P. Research on air pollutant concentration hybrid prediction model and its application in health economic benefit evaluation[D]. Dalian: Dongbei University of Finance and Economics, 2021 (in Chinese). [12] DEVARAPALLI R, BHATTACHARYYA B. Optimal parameter tuning of power oscillation damper by MHHO algorithm[C]// 2019 20th International Conference on Intelligent System Application to Power Systems (ISAP). Piscataway: IEEE Press, 2019: 1-7. [13] ELGAMAL Z M, YASIN N B M, TUBISHAT M, et al. An improved Harris Hawks optimization algorithm with simulated annealing for feature selection in the medical field[J]. IEEE Access, 2020, 8: 186638-186652. doi: 10.1109/ACCESS.2020.3029728 [14] MIRJALILI S, GANDOMI A H. Chaotic gravitational constants for the gravitational search algorithm[J]. Applied Soft Computing, 2017, 53: 407-419. doi: 10.1016/j.asoc.2017.01.008 [15] WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. doi: 10.1109/4235.585893 [16] ALABOOL H M, ALARABIAT D, ABUALIGAH L, et al. Harris Hawks optimization: a comprehensive review of recent variants and applications[J]. Neural Computing and Applications, 2021, 33(15): 8939-8980. doi: 10.1007/s00521-021-05720-5 [17] 赵凯. 樽海鞘与哈里斯鹰优化算法的改进及应用[D]. 郑州: 郑州轻工业大学, 2021.ZHAO K. Improvement and application of salp swarm algorithm and Harris Hawks optimization algorithm[D]. Zhengzhou: Zhengzhou University of Light Industry, 2021 (in Chinese). [18] ABDEL-BASSET M, MOHAMED R, MIRJALILI S, et al. MOEO-EED: a multi-objective equilibrium optimizer with exploration–exploitation dominance strategy[J]. Knowledge-Based Systems, 2021, 214: 106717. doi: 10.1016/j.knosys.2020.106717 [19] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 [20] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279. doi: 10.1109/TEVC.2004.826067 [21] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007 [22] ZITZLER E, DEB K, THIELE L. Comparison of multiobjective evolutionary algorithms: empirical results[J]. Evolutionary Computation, 2000, 8(2): 173-195. doi: 10.1162/106365600568202 [23] ZHANG Q, ZHOU A, ZHAO S, et al. Multiobjective optimization test instances for the CEC 2009 special session and competition[C]//Special Session on Performance Assessment of Multi-objective Optimization Algorithms. Colchester: University of Essex, 2008: 1-30. [24] RIQUELME N, VON LÜCKEN C, BARAN B. Performance metrics in multi-objective optimization[C]// 2015 Latin American Computing Conference (CLEI). Piscataway: IEEE Press, 2015: 1-11. [25] JIAO R W, SUN Y Z, SUN J Q, et al. Antenna design using dynamic multi-objective evolutionary algorithm[J]. IET Microwaves, Antennas & Propagation, 2018, 12(13): 2065-2072. [26] TAN Q L, LU F, JI Y H, et al. LC temperature-pressure sensor based on HTCC with temperature compensation algorithm for extreme 1100 ℃ applications[J]. Sensors and Actuators A: Physical, 2018, 280: 437-446. doi: 10.1016/j.sna.2018.08.021 [27] GODIO A, SANTILANO A. On the optimization of electromagnetic geophysical data: application of the PSO algorithm[J]. Journal of Applied Geophysics, 2018, 148: 163-174. doi: 10.1016/j.jappgeo.2017.11.016 -
下载:
点击查看大图
计量
- 文章访问数: 249
- HTML全文浏览量: 101
- PDF下载量: 1
- 被引次数: 0
