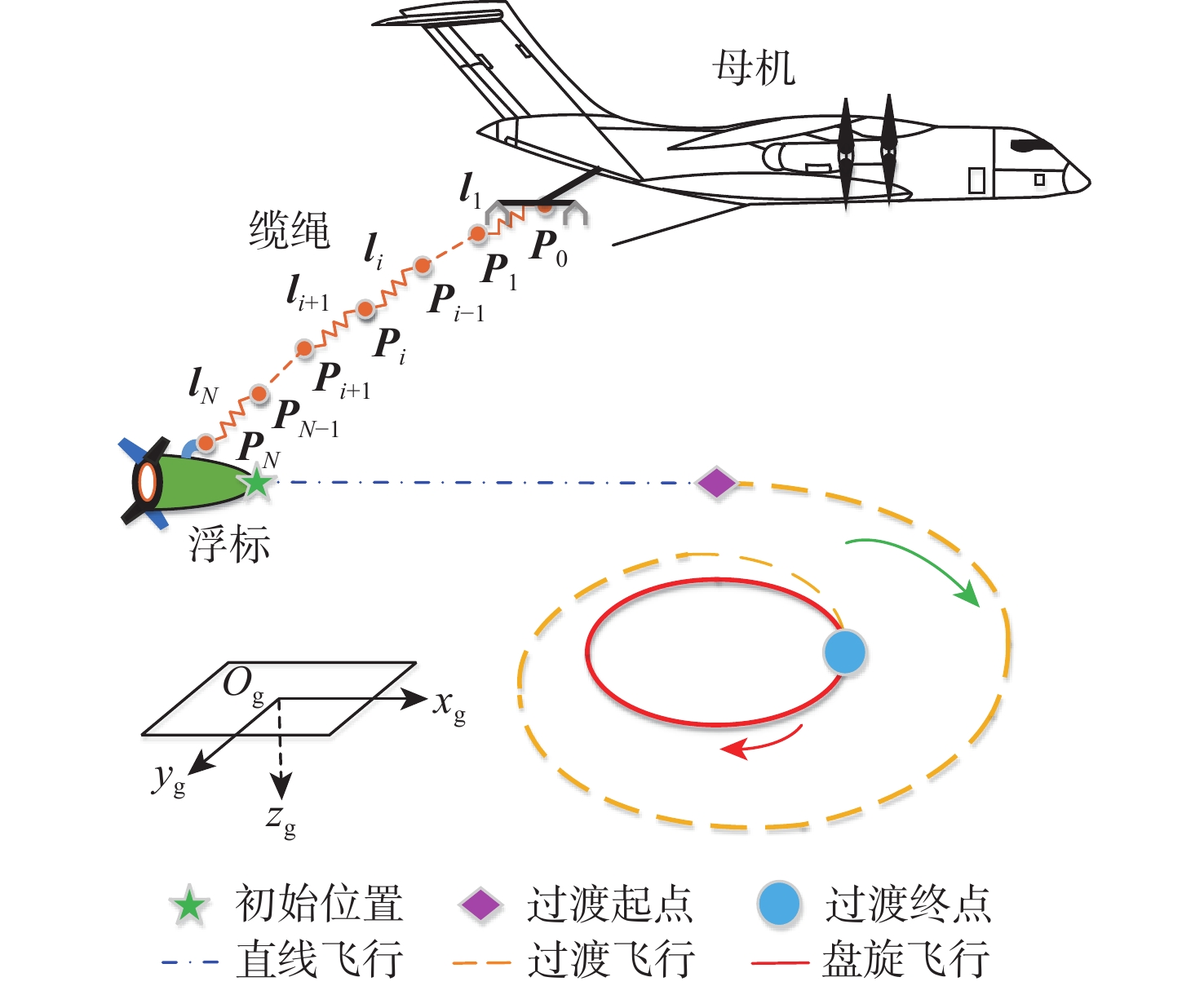
Trajectory design for straight-circulating flight transition of aerial recovery towing system
-
摘要:
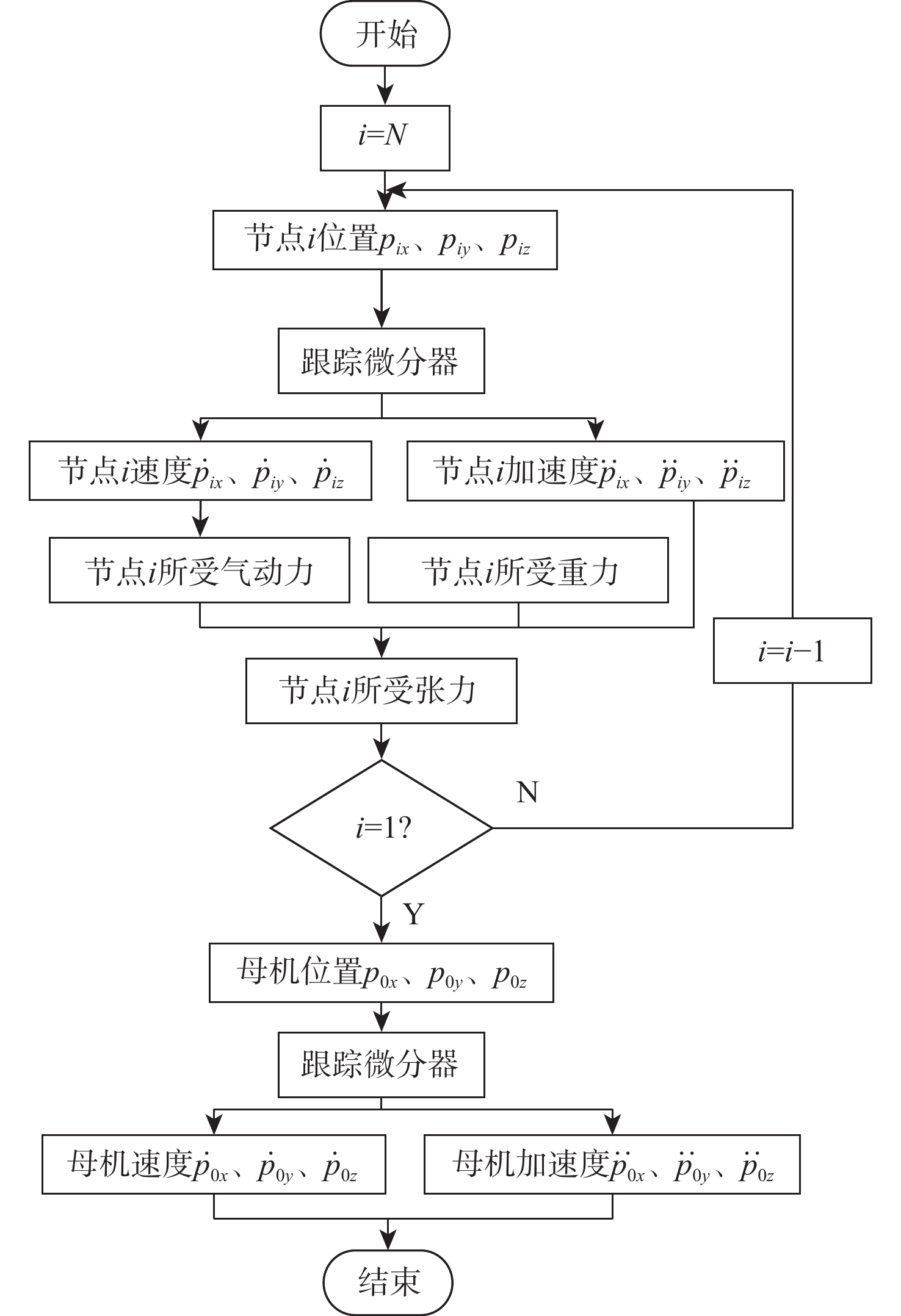
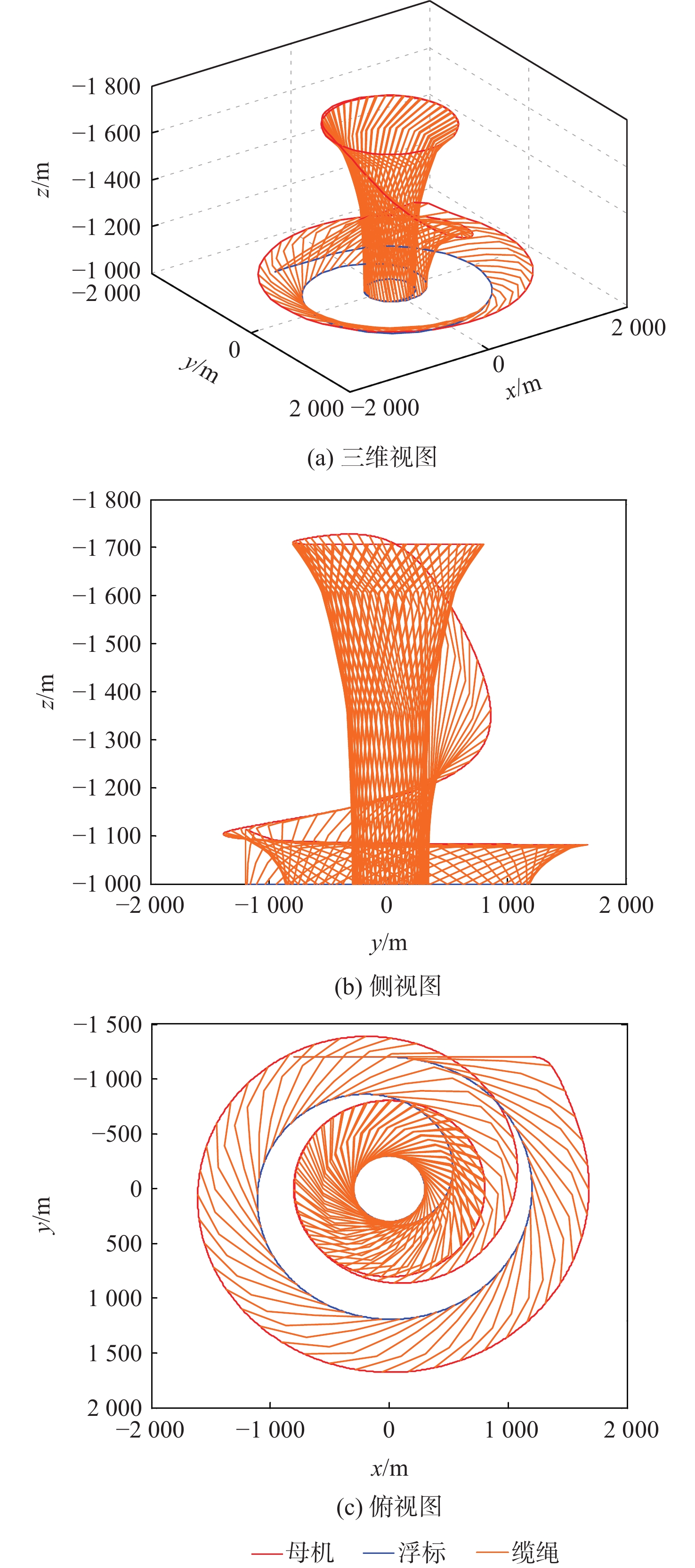
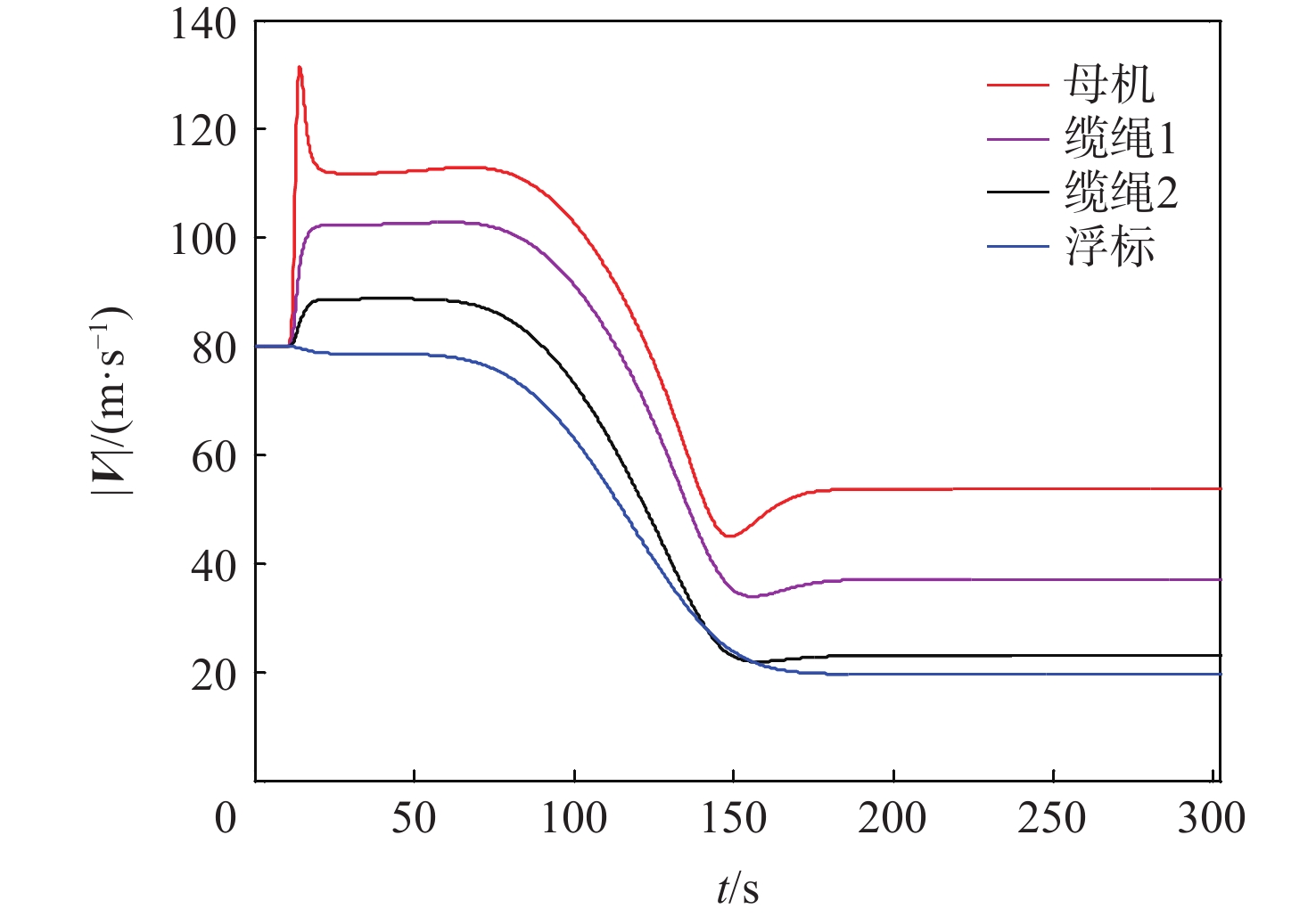
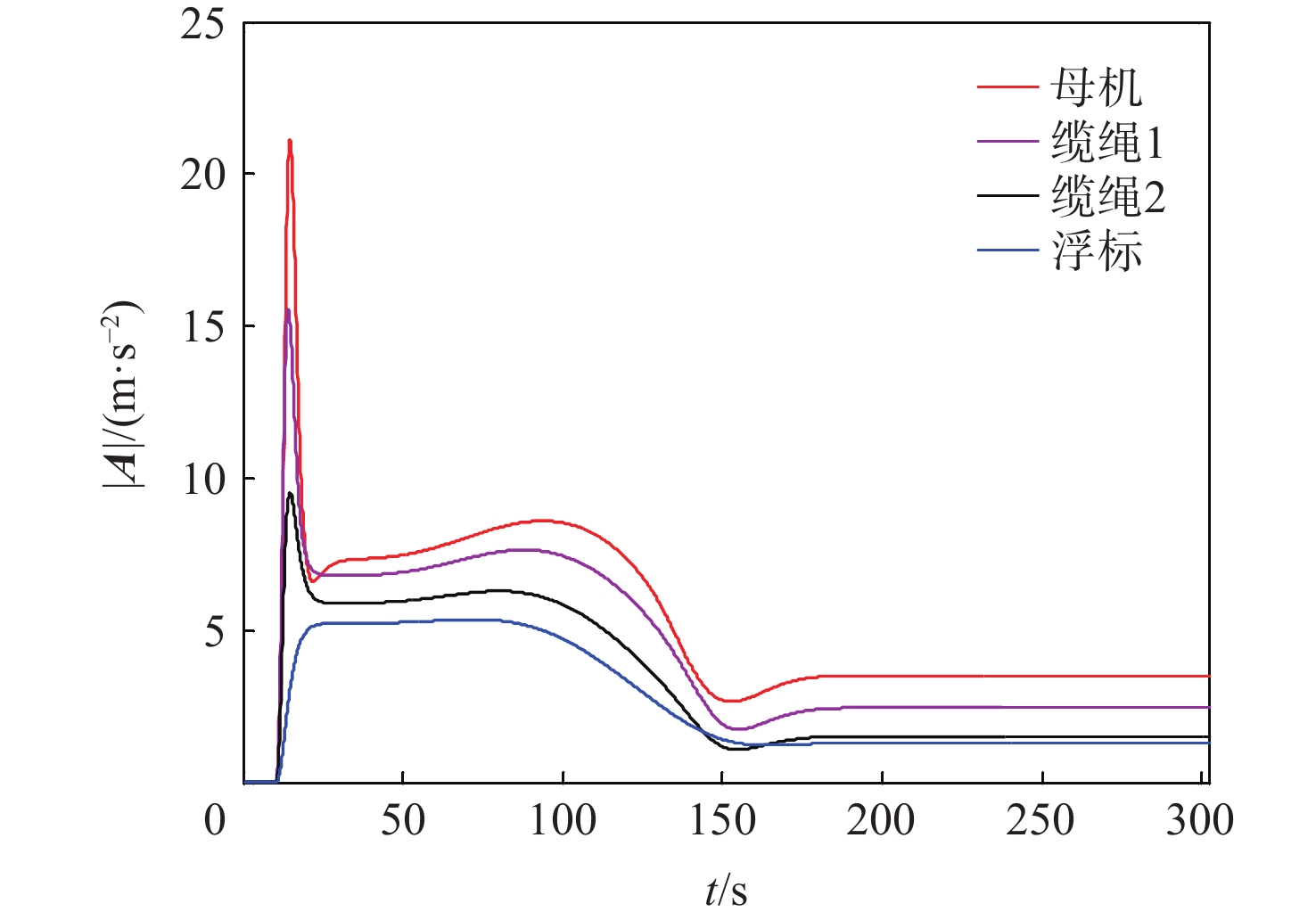
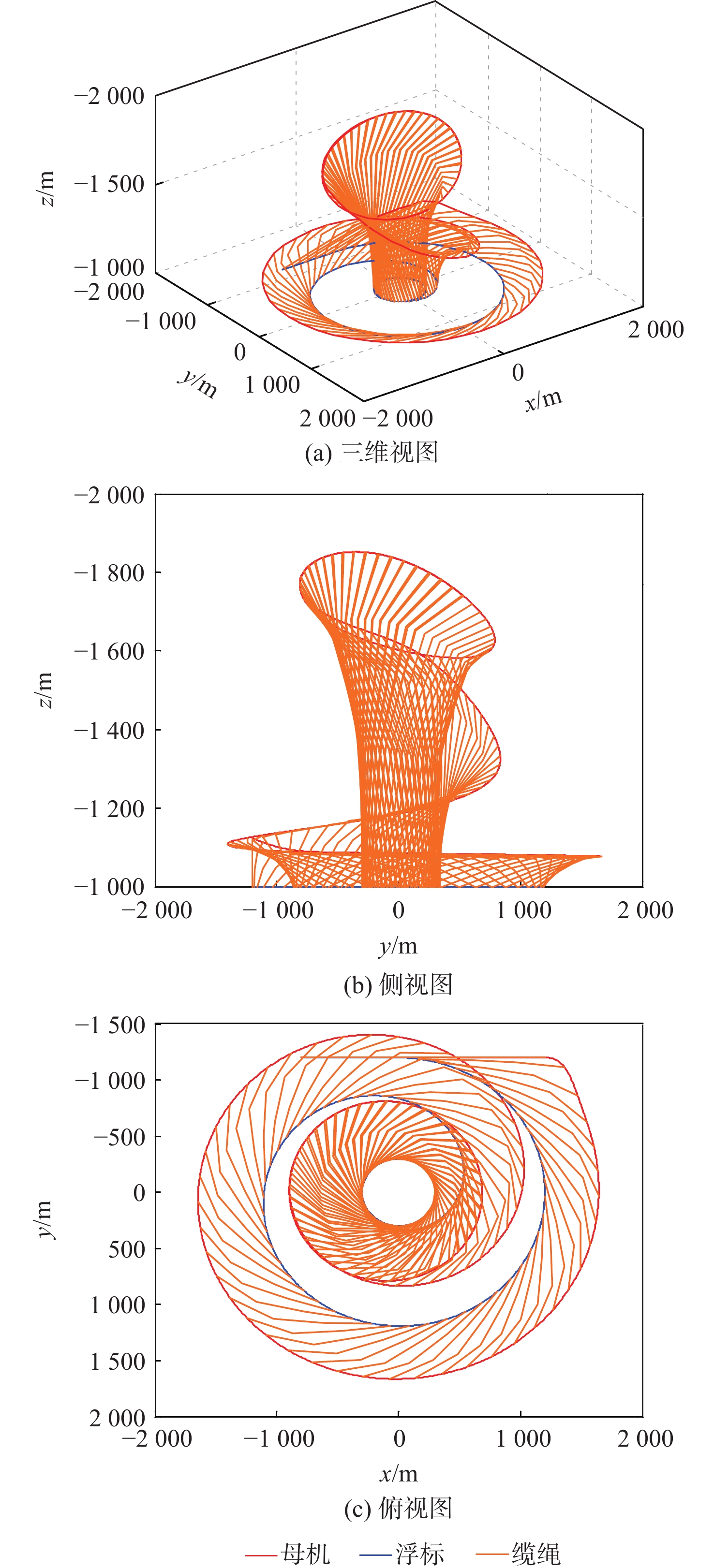
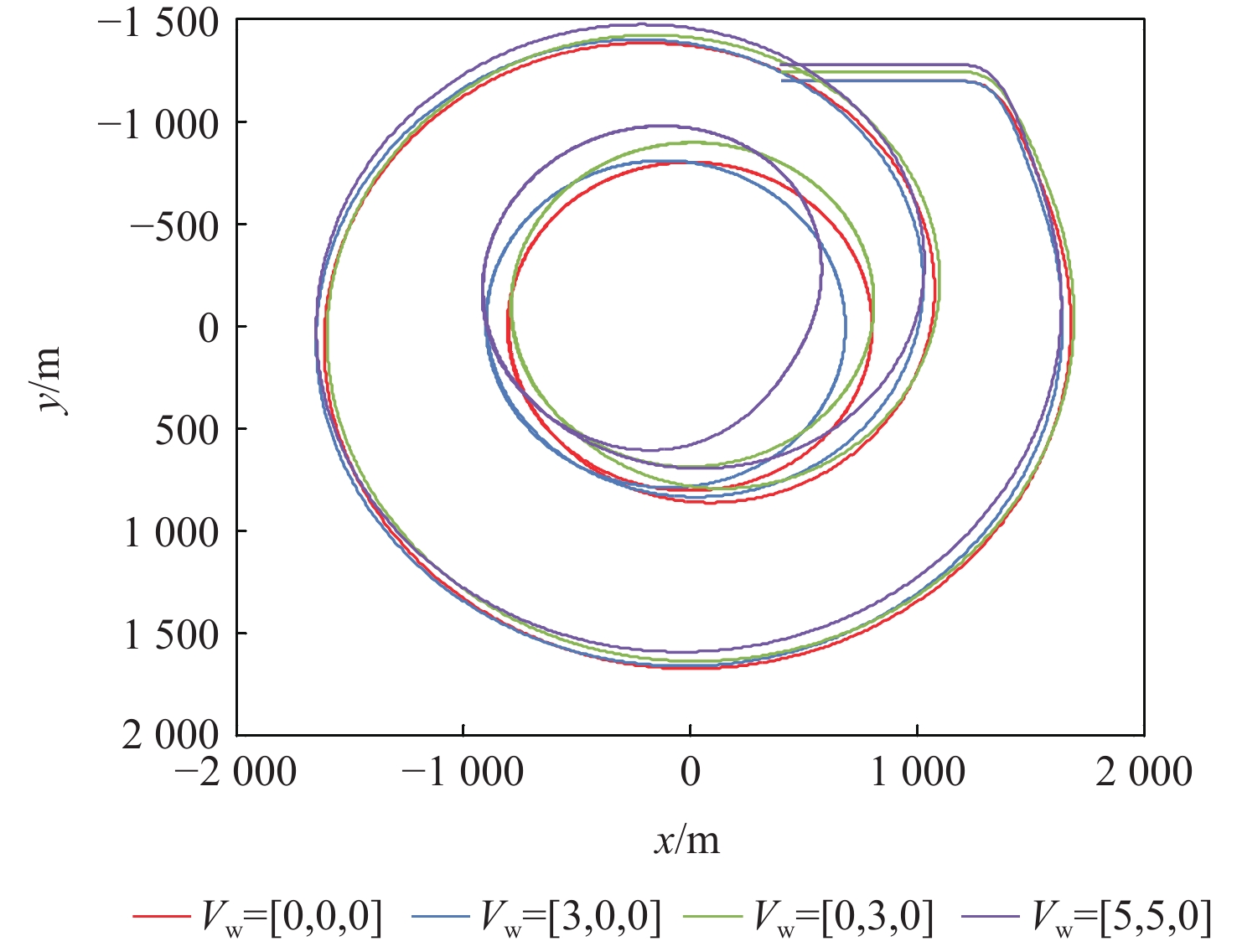
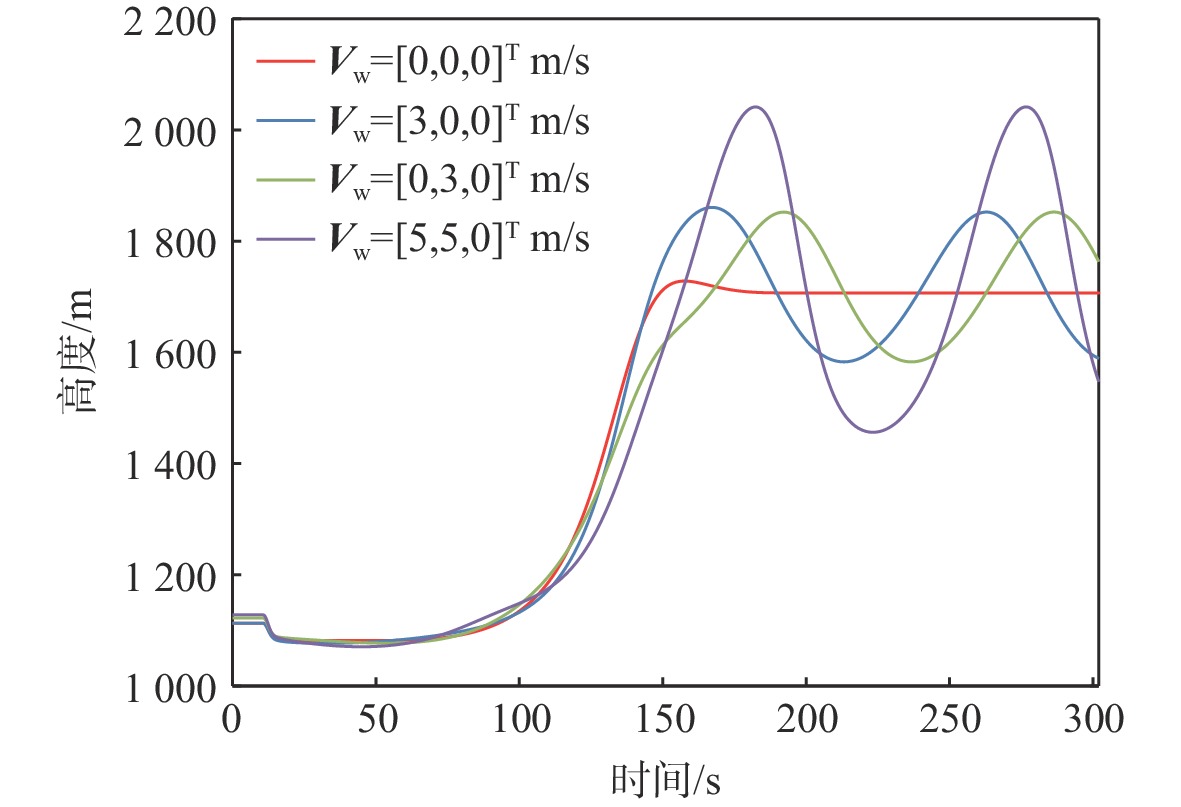
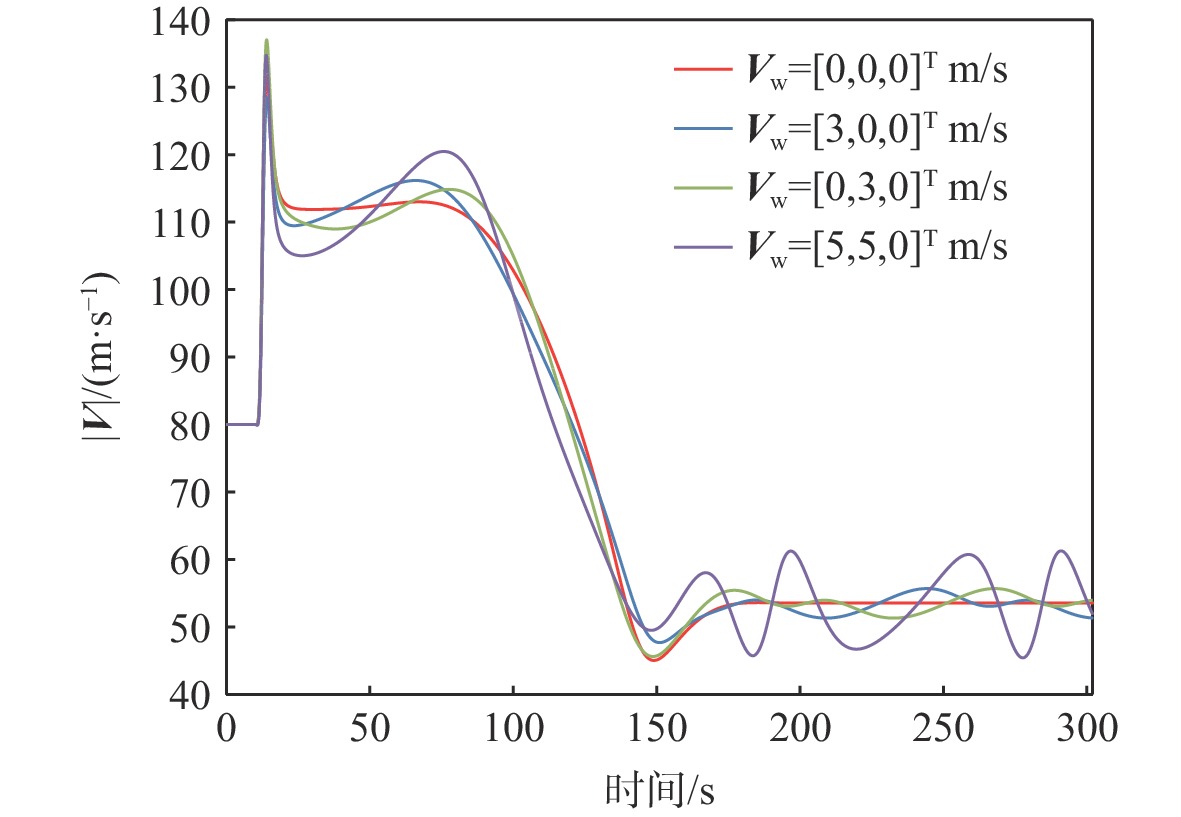
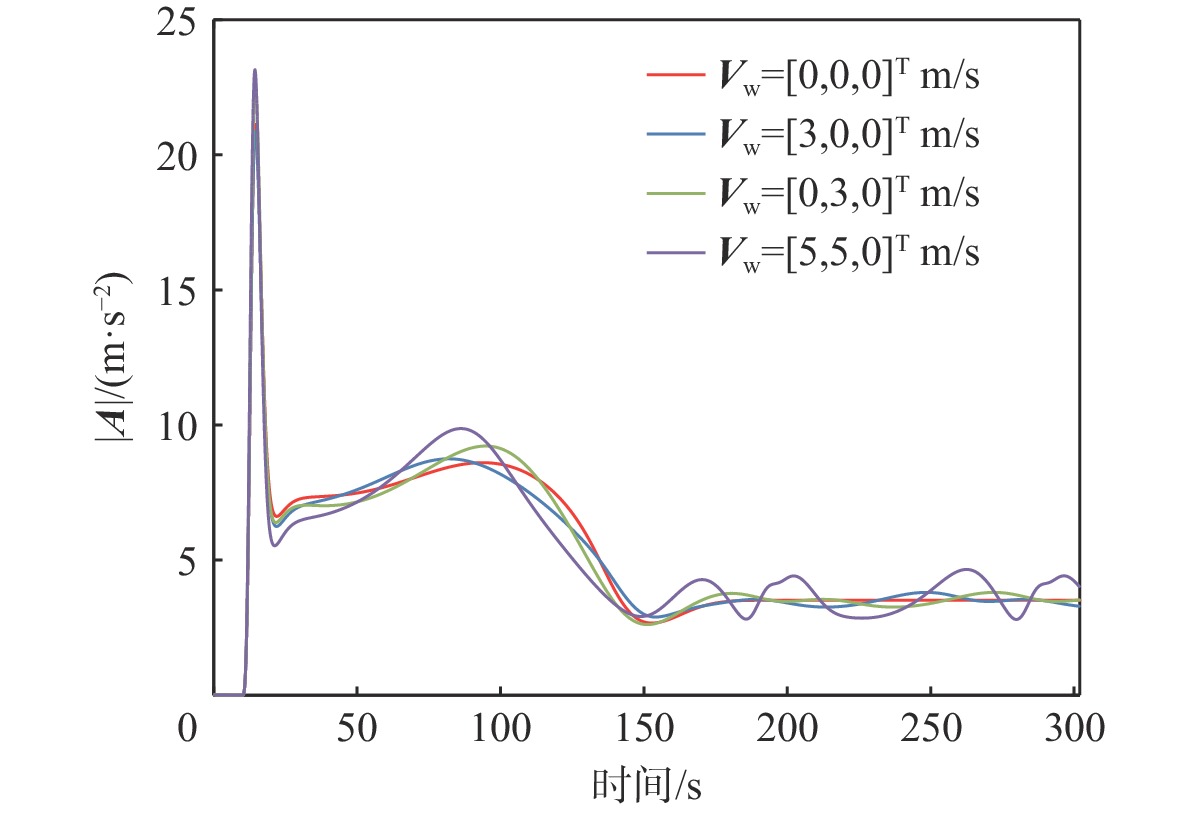
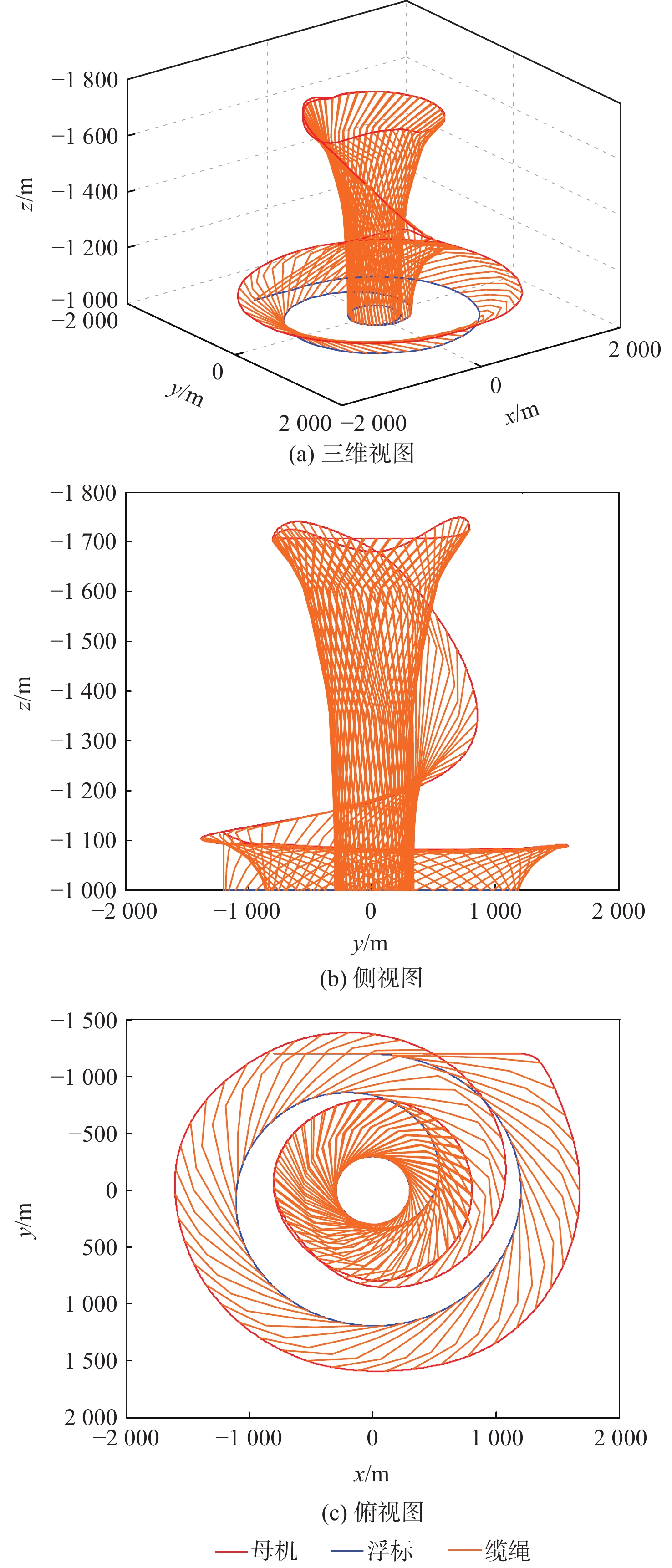
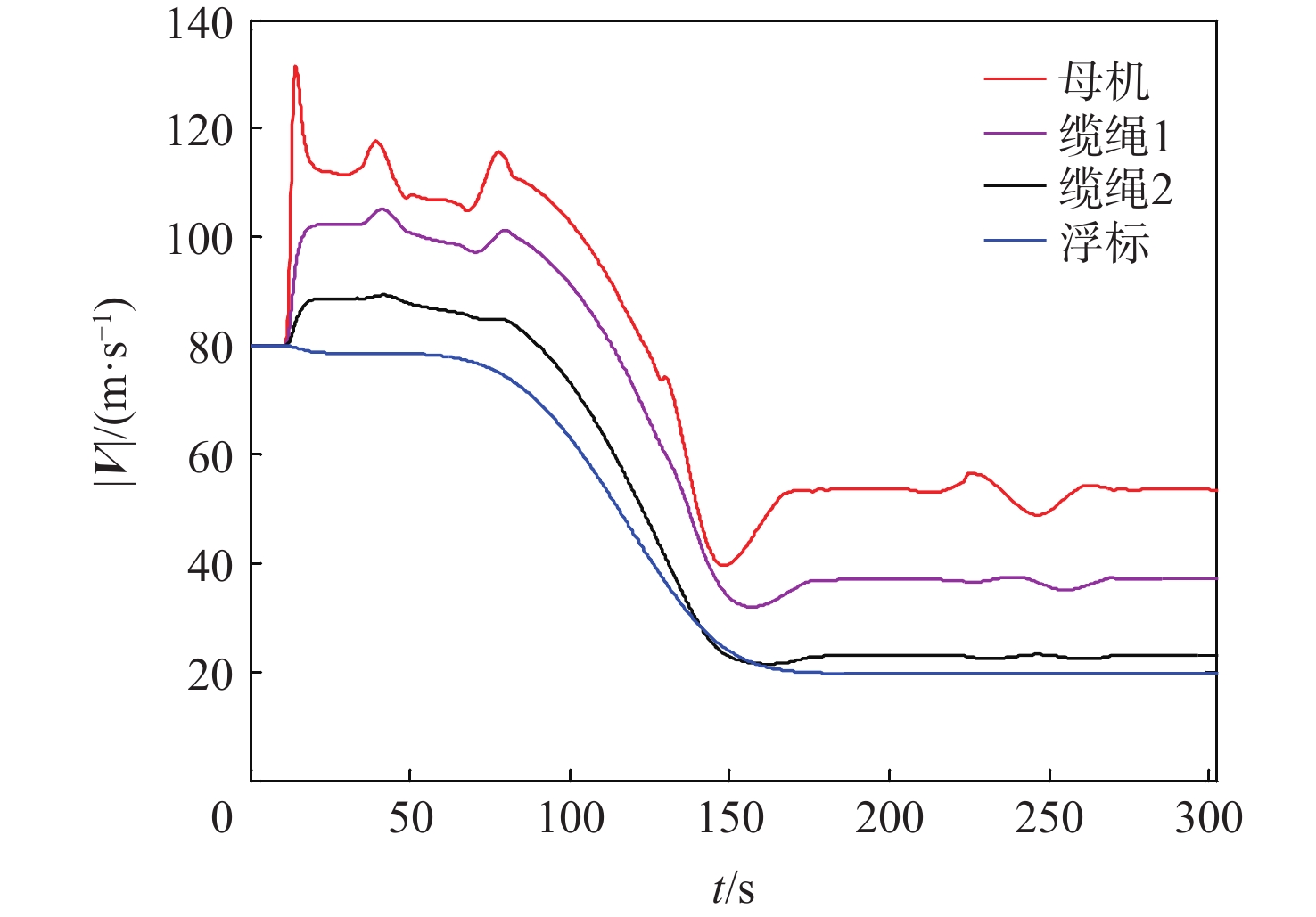
针对气流扰动下空基回收拖曳系统在直线-盘旋转接段飞行过程中的拖曳浮标稳定问题，提出一种基于微分平坦理论的拖曳系统转接段运动轨迹的设计方法，通过设计母机运动轨迹间接地控制拖曳浮标沿着预设的转接轨迹安全、平稳、精准地转接飞行。采用质点-弹簧离散缆绳模型构建母机-缆绳-浮标组合体多体动力学模型；在证明拖曳系统具备微分平坦特性的基础上，以拖曳浮标三轴位置为平坦输出，所提方法以期浮标沿着预设安全转接段轨迹飞行；结合拖曳浮标直线飞行状态与盘旋飞行状态设计拖曳浮标转接段飞行轨迹。通过平静大气、多种常值风及阵风气流扰动场景下的仿真算例结果表明，所提方法能够实现拖曳浮标在直线-盘旋转接段的稳定飞行。
Abstract:To handle the stabilization problem of the towed buoy in the straight-circulating flight transition process of the aerial recovery towing system under airflow disturbances, a trajectory design method for the transition process of the towing system based on differential flatness theory was proposed. By designing the trajectory of the mothership, the towed buoy was indirectly controlled to fly safely, smoothly, and accurately along the preset transition trajectory. Firstly, the mass-spring discrete cable model was used to construct the multi-body dynamic model of the mothership-cable-buoy. Secondly, after proving that the towing system was differentially flat, a trajectory design method of the towing system based on differential flatness theory was proposed by taking the three-axis position of the towed buoy as the flat output so that the buoy could fly along the preset safe transition trajectory. Subsequently, the straight and circulating flight states of the towed buoy were analyzed to design the flight trajectory of the towed buoy in the transition section. Finally, the simulation examples under a calm atmosphere, various constant wind, and gust turbulence scenarios show that the proposed method can achieve stable flight of the towed buoy in the straight-circulating transition section.
-
Key words:
- aerial recovery /
- UAV /
- trajectory design /
- differential flatness /
- flight in transition section
-
图 2 基于微分平坦的轨迹规划算法流程
Figure 2. Flow chart of trajectory planning algorithm based on differential flatness
图 7 3 m/s常值风下拖曳系统轨迹
Figure 7. Trajectory of towing system under constant wind of 3 m/s
图 8 不同常值风扰动下母机轨迹俯视
Figure 8. Vertical view of mothership trajectory under different constant winds
图 11 不同常值风扰动下母机加速度
Figure 11. Acceleration of mothership under different constant winds
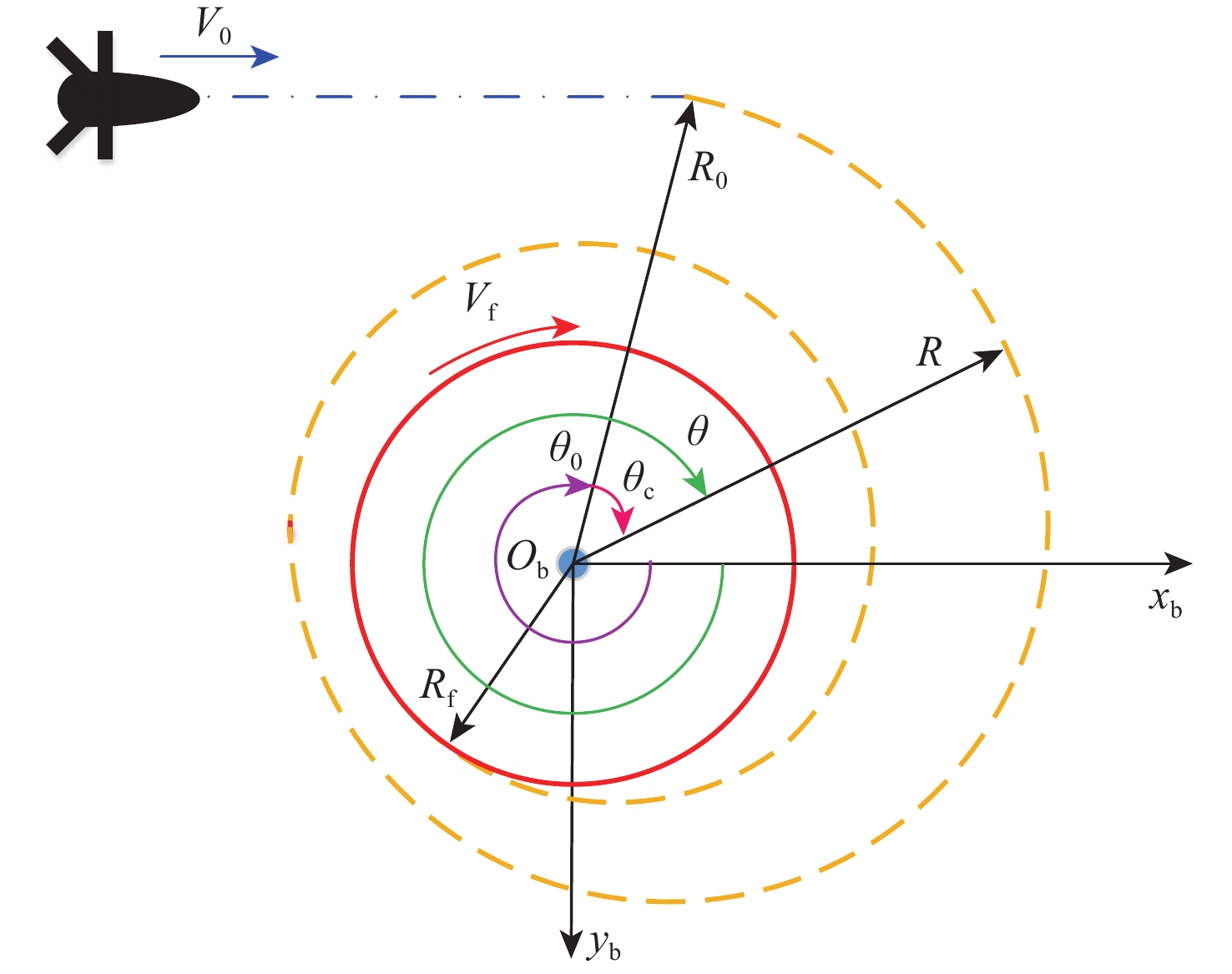
参数 数值 浮标高度$H$/m 1000 直线速度$V_0^{}$/(m·s−1) 80 盘旋速度$V_{\mathrm{f}}^{}$/(m·s−1) 20 初始半径${R_0}$/m 1200 终点半径${R_{\mathrm{f}}}$/m 300 转接过渡开始时刻${t_0}$/s 10 转接过渡飞行时间$T$/s 200 仿真时间${t_{\mathrm{e}}}$/s 304 初始偏航角${\theta _0}$/(°) 270 
下载: 导出CSV
表 2 缆绳-浮标参数
Table 2. Parameters of cable-buoy
参数 数值 缆绳长度${l_0}$/m 400 缆绳密度${\rho _l}$/(kg·m−3) 970 缆绳直径${d_l}$/m 2×10−3 缆绳弹性模量${E}$/Pa 1.2×1011 浮标质量${m_{{\text{dr}}}}$/kg 30 浮标气动面积$ {S_{{{\mathrm{dr}}}}} $/m2 0.785 浮标阻力系数$ C_{{{\mathrm{dr}}}}^{{\mathrm{D}}} $ 0.42 浮标升力系数$ C_{{{\mathrm{dr}}}}^{{\mathrm{L}}} $ 0.01
下载: 导出CSV
-
[1] 刘永孛. 集群无人机空基回收任务规划方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021: 3-11.LIU Y B. Research on mission planning methods for aerial recovery of unmanned aerial vehicle swarms[D]. Harbin: Harbin Institute of Technology, 2021: 3-11(in Chinese). [2] 曹莉, 耿斌斌, 周亮, 等. 无人机集群发射与回收技术发展研究[J]. 空天防御, 2019, 2(2): 68-72.CAO L, GENG B B, ZHOU L, et al. Research on UAVS launch and recovery technology development[J]. Air & Space Defense, 2019, 2(2): 68-72(in Chinese). [3] SUN L, CASTAGNO J D, HEDENGREN J D, et al. Parameter estimation for towed cable systems using moving horizon estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1432-1446. doi: 10.1109/TAES.2014.130642 [4] WILLIAMS P, TRIVAILO P. Dynamics of circularly towed aerial cable systems, Part 2: Transitional flight and deployment control[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 766-779. doi: 10.2514/1.20434 [5] 苏子康, 李春涛, 余跃, 等. 绳系拖曳飞行器高抗扰轨迹跟踪控制[J]. 北京航空航天大学学报, 2021, 47(11): 2234-2248.SU Z K, LI C T, YU Y, et al. High anti-disturbance trajectory tracking control for cable towed vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(11): 2234-2248(in Chinese). [6] MERZ M, JOHANSEN T A. Control of an end body towed by a circling unmanned aerial vehicle[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(12): 2677-2686. doi: 10.2514/1.G004199 [7] RO K, KUK T, KAMMAN J W. Dynamics and control of hose-drogue refueling systems during coupling[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1694-1708. doi: 10.2514/1.53205 [8] 方晓星, 王勇, 王英勋. 低空掠海飞行拖靶自抗扰高度控制律设计[J]. 南京理工大学学报, 2012, 36(5): 835-839.FANG X X, WANG Y, WANG Y X. Design of active disturbances rejection control law of low altitude sea-skimming tow target[J]. Journal of Nanjing University of Science and Technology, 2012, 36(5): 835-839(in Chinese). [9] SU Z K, LI C T, WU J F, et al. Neuro-adaptive prescribed performance control for aerial-recovery drogue with actuator constraints[J]. Journal of Guidance, Control, and Dynamics, 2022, 45(8): 1451-1465. doi: 10.2514/1.G005679 [10] WILLIAMS P. Optimization of circularly towed cable system in crosswind[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1251-1263. doi: 10.2514/1.45241 [11] SUN L, HEDENGREN J D, BEARD R W. Optimal trajectory generation using model predictive control for aerially towed cable systems[J]. Journal of Guidance, Control, Dynamics, 2014, 37(2): 525-539. doi: 10.2514/1.60820 [12] MURRAY R M. Trajectory generation for a towed cable system using differential flatness[J]. IFAC Proceedings Volumes, 1996, 29(1): 2792-2797. doi: 10.1016/S1474-6670(17)58099-4 [13] WILLIAMS P, LAPTHORNE P, TRIVAILO P. Circularly-towed lumped mass cable model validation from experimental data[C]// Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Reston: AIAA, 2006. [14] WILLIAMS P, SGARIOTO D, TRIVAILO P. Motion planning for an aerial-towed cable system[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2005. [15] WILLIAMS P, TRIVAILO P. Dynamics of circularly towed aerial cable systems, Part I: Optimal configurations and their stability[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 753-765. doi: 10.2514/1.20433 [16] 周孝添, 任宏斌, 苏波, 等. 基于微分平坦的分层轨迹规划算法[J]. 兵工学报, 2023, 44(2): 394-405.ZHOU X T, REN H B, SU B, et al. Hierarchical trajectory planning algorithm based on differential flatness[J]. Acta Armanmentarii, 2023, 44(2): 394-405(in Chinese). [17] 丛岩峰, 安向京, 陈虹, 等. 基于滚动优化原理的类车机器人路径跟踪控制[J]. 吉林大学学报(工学版), 2012, 42(1): 182-187.CONG Y F, AN X J, CHEN H, et al. Path following control of car-like robot based on rolling windows[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(1): 182-187(in Chinese). [18] CHAMSEDDINE A, ZHANG Y M, RABBATH C A, et al. Flatness-based trajectory planning/replanning for a quadrotor unmanned aerial vehicle[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 2832-2848. doi: 10.1109/TAES.2012.6324664 [19] ZHAO D, MISHRA S, GANDHI F. A differential-flatness-based approach for autonomous helicopter shipboard landing[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(3): 1557-1569. doi: 10.1109/TMECH.2021.3085696 [20] WILLIAMS P, SGARIOTO D, TRIVAILO P M. Constrained path-planning for an aerial-towed cable system[J]. Aerospace Science and Technology, 2008, 12(5): 347-354. doi: 10.1016/j.ast.2007.08.006 [21] 朱延娟, 罗丹. 飞机圆周盘旋时托缆的动力学建模与分析[J]. 同济大学学报(自然科学版), 2018, 46(1): 81-86.ZHU Y J, LUO D. Dynamics modeling and simulation of circularly aerial towed cable systems[J]. Journal of Tongji University (Natural Science), 2018, 46(1): 81-86(in Chinese). [22] 肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993: 27-48.XIAO Y L, JIN C J. Flight principle in atmospheric disturbance [M]. Beijing: National Defense Industry Press, 1993: 27-48(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 113
- HTML全文浏览量: 77
- PDF下载量: 4
- 被引次数: 0
