-
摘要:
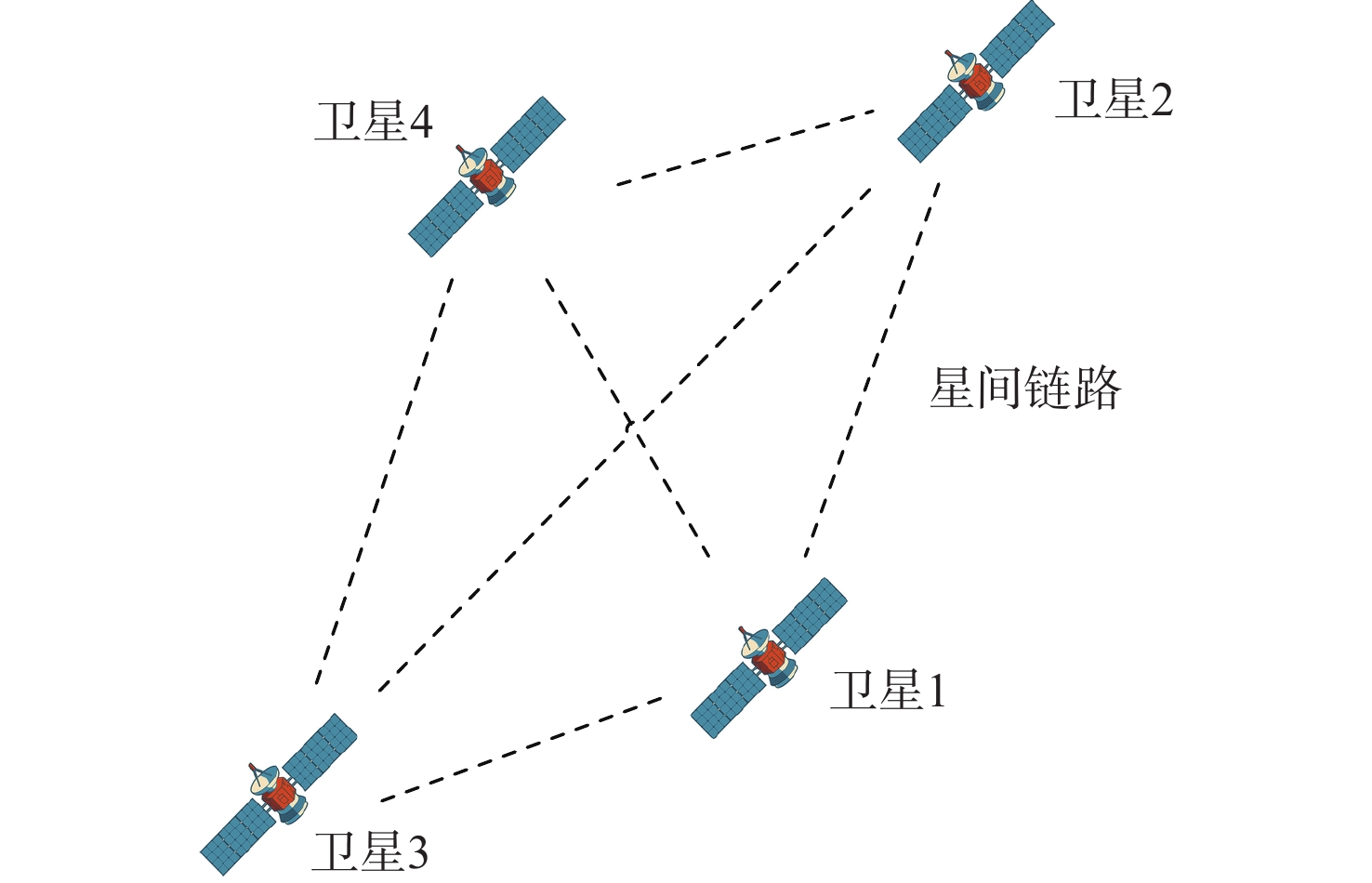
针对卫星星座自主导航系统中存在的模型不确定性及难以准确获取的时变系统噪声统计特性影响导航精度的问题，提出了一种系统噪声在线自适应调整的UKF算法。基于所提出的自适应UKF算法设计了一种基于星间相对测量的卫星星座自主导航方法，该方法结合奇异值分解和比例修正的采样策略，解决了应用UKF时易出现状态误差方差阵丧失正定性而导致的Cholesky分解无法进行的问题。通过在低轨区域星座和中轨全球星座上的仿真实验，验证了该算法在提高滤波精度以及改善状态估计置信度方面的有效性，所提算法的定轨精度优于EKF算法、自适应EKF算法以及基于对称采样策略的UKF算法。采用CRLB分析法对导航算法的估计性能进行了分析验证。
Abstract:The autonomous satellite constellation navigation system faces model uncertainty and is difficult to accurately obtain statistical characteristics of the time-varying system noise, thus affecting the navigation accuracy. To address this issue, an unscented Kalman filter (UKF) algorithm based on the online adaptive adjustment of system noise was proposed. An autonomous satellite constellation navigation method based on the relative measurement between satellites was designed according to the proposed adaptive UKF algorithm. This method combined the sampling strategy of singular value decomposition and scale correction to solve the problem that Cholesky decomposition cannot be carried out due to the loss of positive definiteness of the state error variance matrix when UKF was applied. Through the simulation results on a low earth orbit (LEO) local constellation and a middle earth orbit (MEO) global constellation, the effectiveness of the algorithm in improving the filtering accuracy and the confidence of state estimation was verified. Its orbit determination accuracy was better than the extended Kalman filter (EKF) algorithm, adaptive EKF algorithm, and UKF algorithm based on symmetrical sampling strategies. Finally, the Cramer-Rao lower bounds (CRLB) analysis method was used to verify the estimation performance of the algorithm.
-
Key words:
- autonomous constellation navigation /
- EKF /
- UKF /
- adaptive filtering /
- CRLB
-
图 4 新息统计值随遗忘因子的变化趋势
Figure 4. Variation of innovation statistics with forgetting factor
图 5 新息统计值随遗忘因子变化的趋势
Figure 5. Variation of innovation statistics with forgetting factor
图 10 AUKF算法切换前后卫星1位置误差
Figure 10. Position error of satellite 1 before and after AUKF algorithm switching
图 11 AUKF算法切换前后卫星1速度误差
Figure 11. Velocity error of satellite 1 before and after AUKF algorithm switching
图 12 AUKF算法切换后卫星1位置误差
Figure 12. Position error of satellite 1 after AUKF algorithm switching
图 13 AUKF算法切换后卫星1速度误差
Figure 13. Velocity error of satellite 1 after AUKF algorithm switching
图 14 不同滤波算法下位置误差对比
Figure 14. Comparison of position error under different filtering algorithms
图 15 不同滤波算法下速度误差对比
Figure 15. Comparison of velocity errors under different filtering algorithms
表 1 星座卫星初始轨道参数
Table 1. Initial orbit parameters of constellation satellites
卫星
编号轨道
半长轴/km偏心率 轨道
倾角/(°)近地点
幅角/(°)升交点
赤经真近点
角/(°)1 7478.14 0.00 63.14 0.00 0.85 0.50 2 7478.14 0.00 62.00 0.00 0.00 3.00 3 7478.14 0.00 62.00 0.00 0.00 359.20 4 7478.14 0.00 63.14 0.00 0.00 1.80 
下载: 导出CSV
表 2 不同星座构型下的导航误差统计
Table 2. Statistics of navigation errors under different constellation configurations
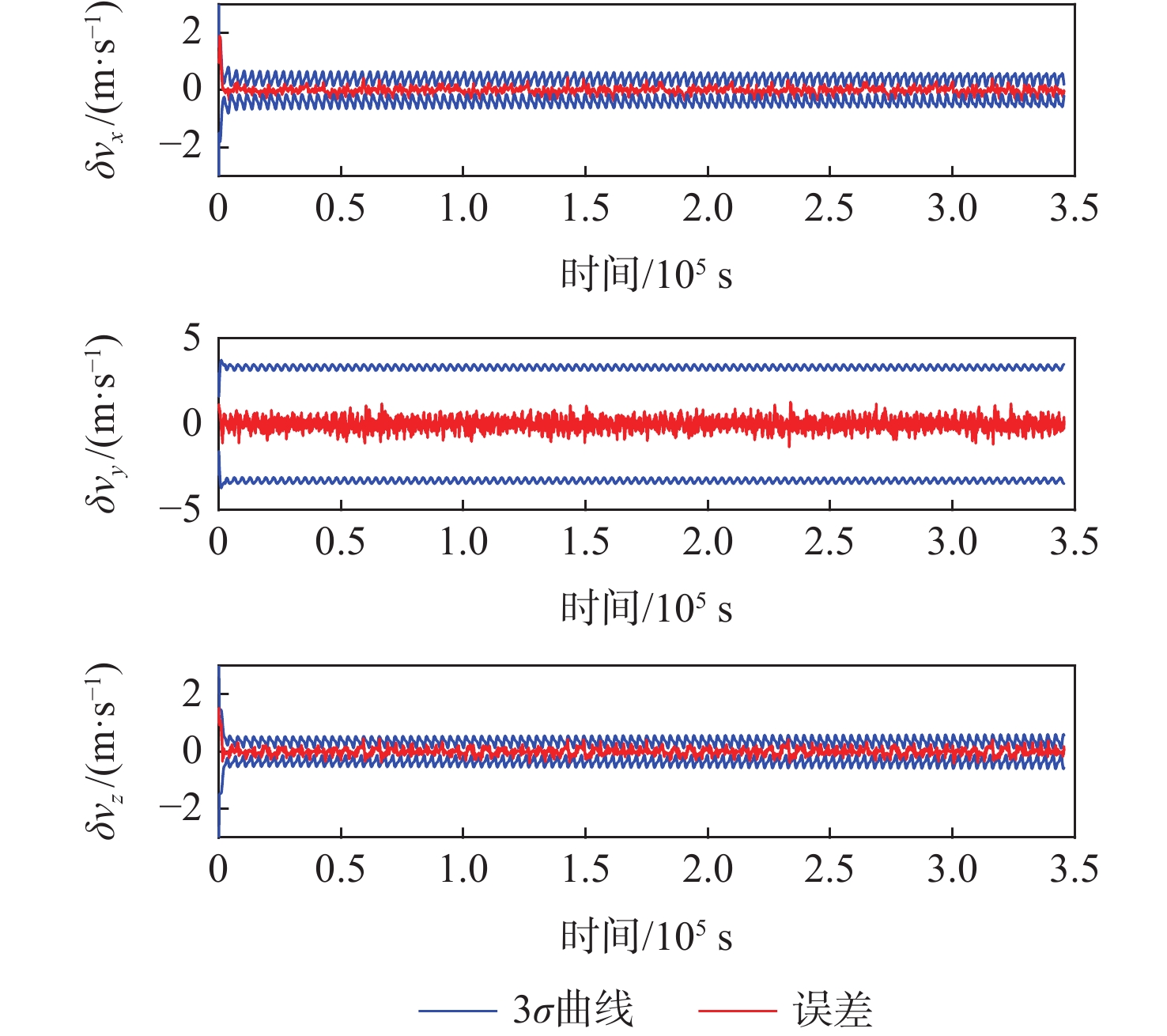
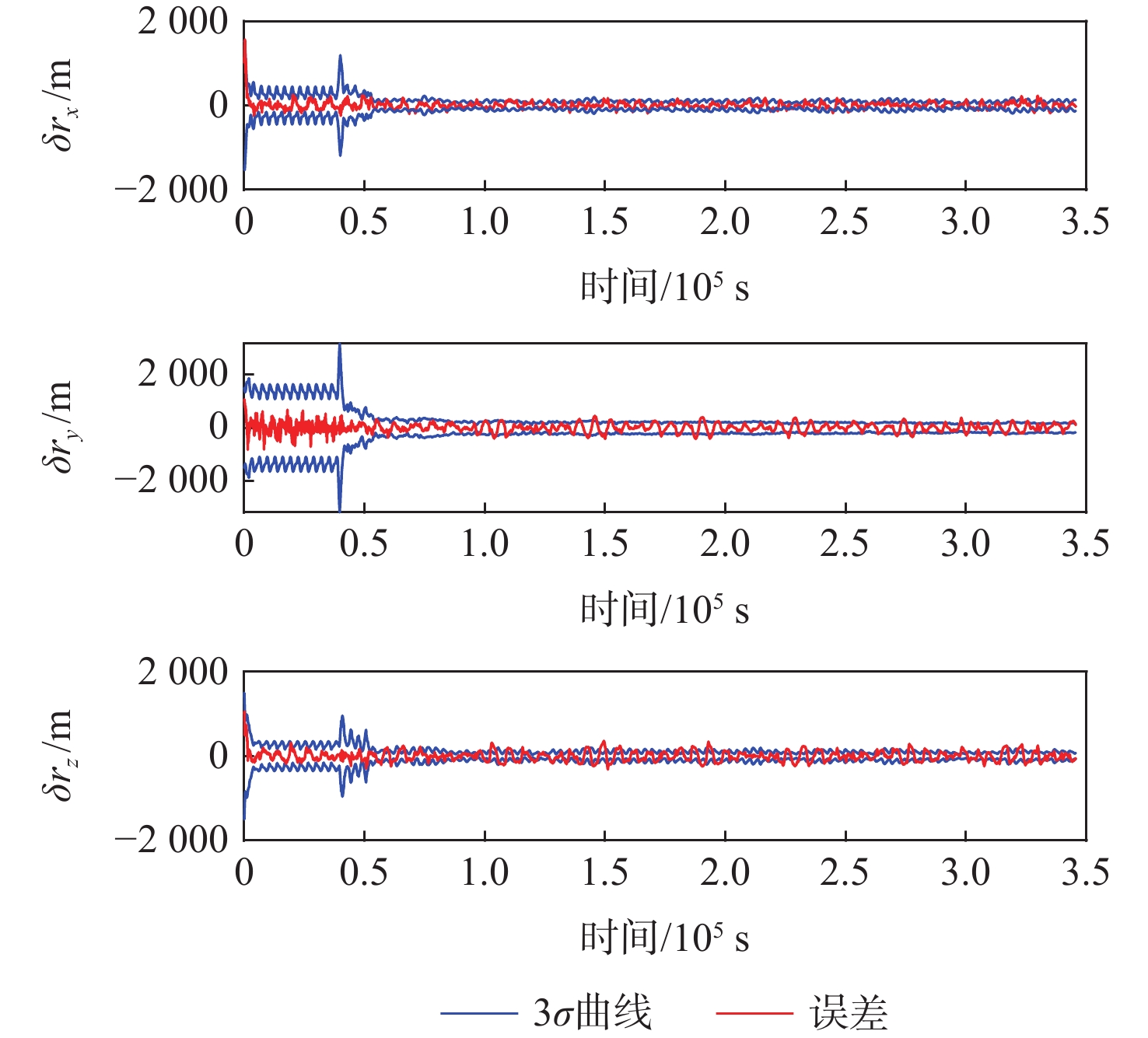
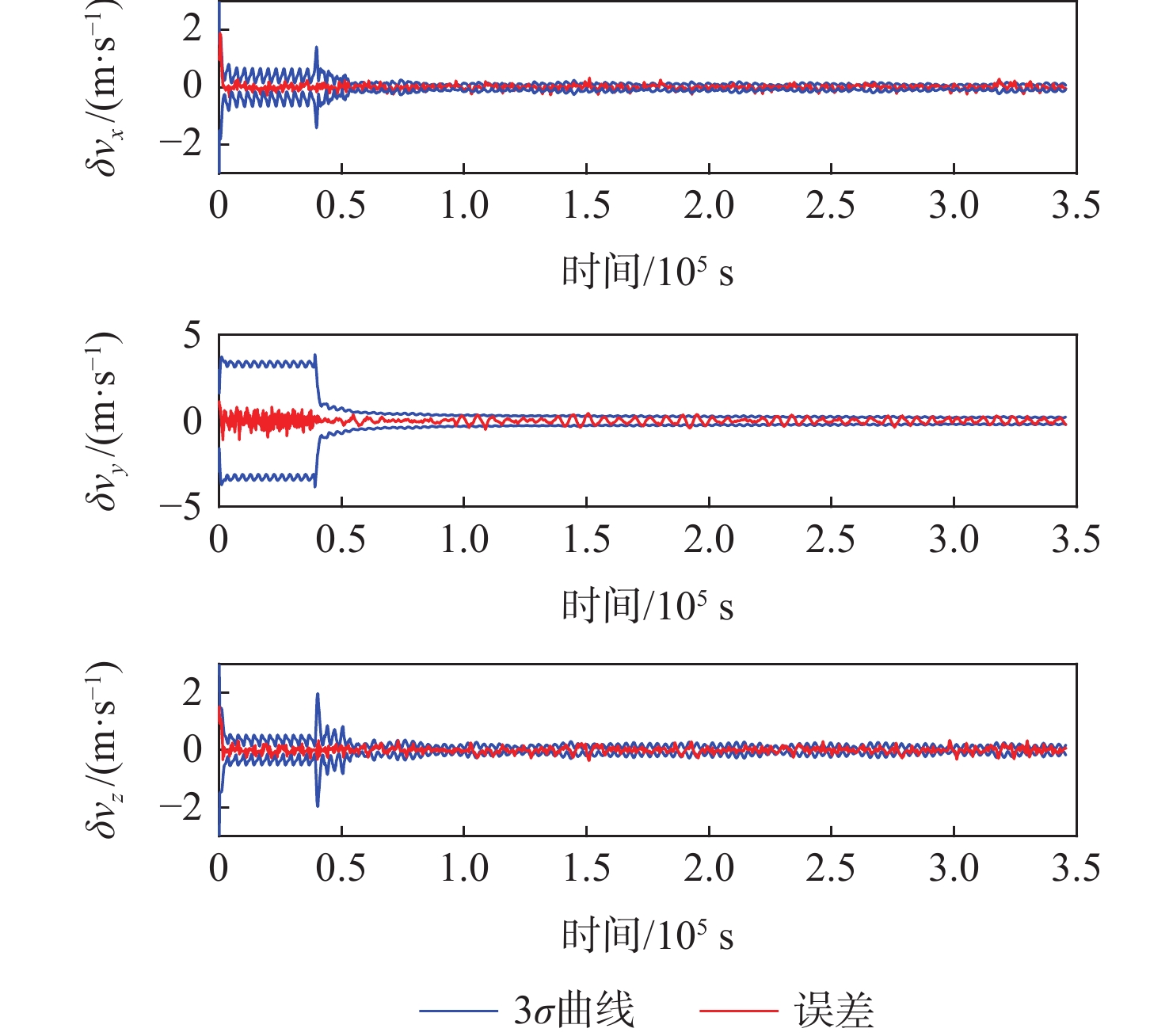
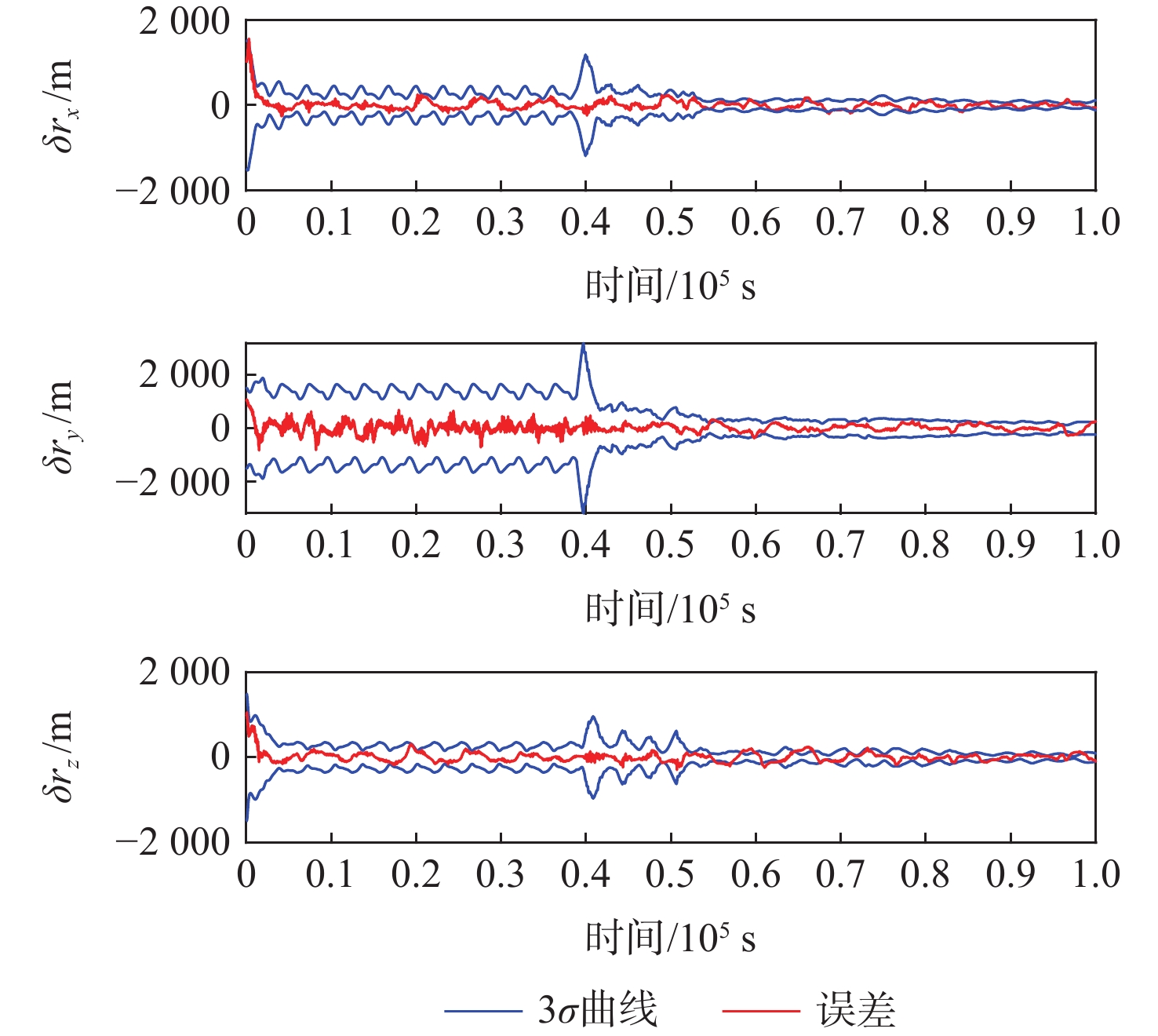
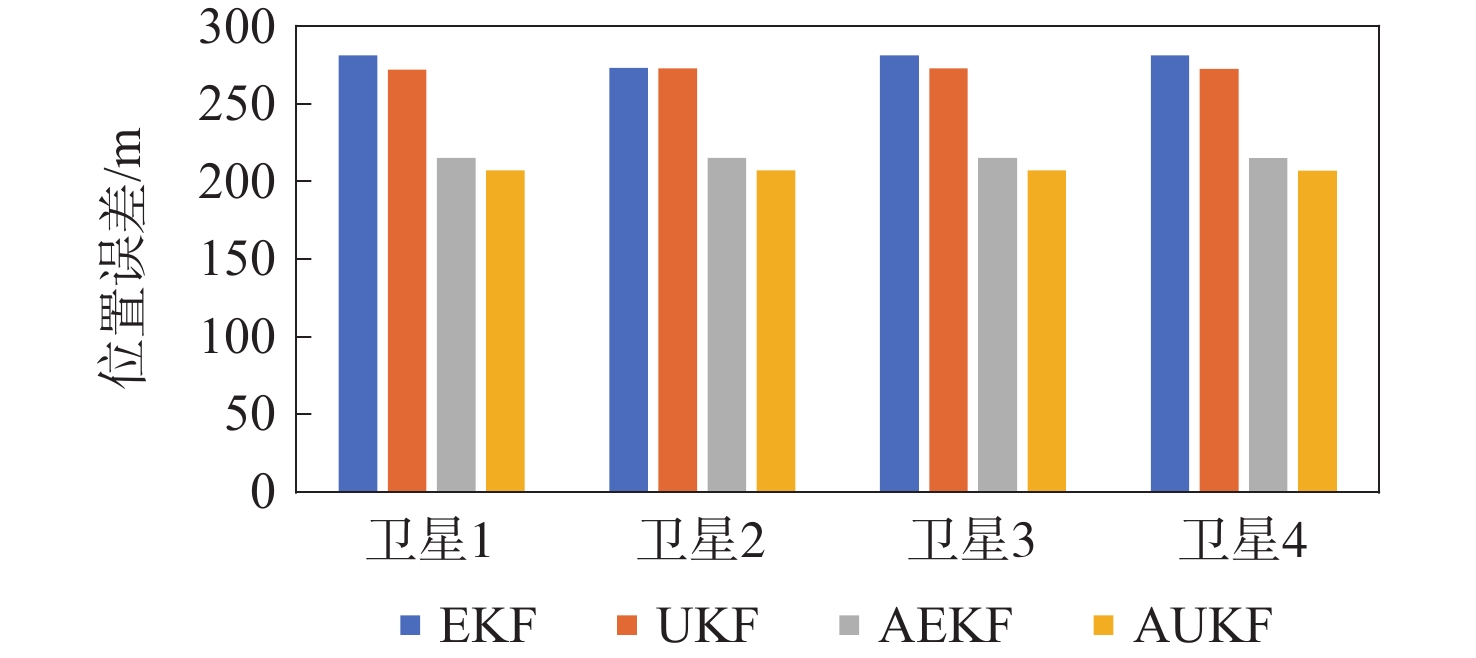
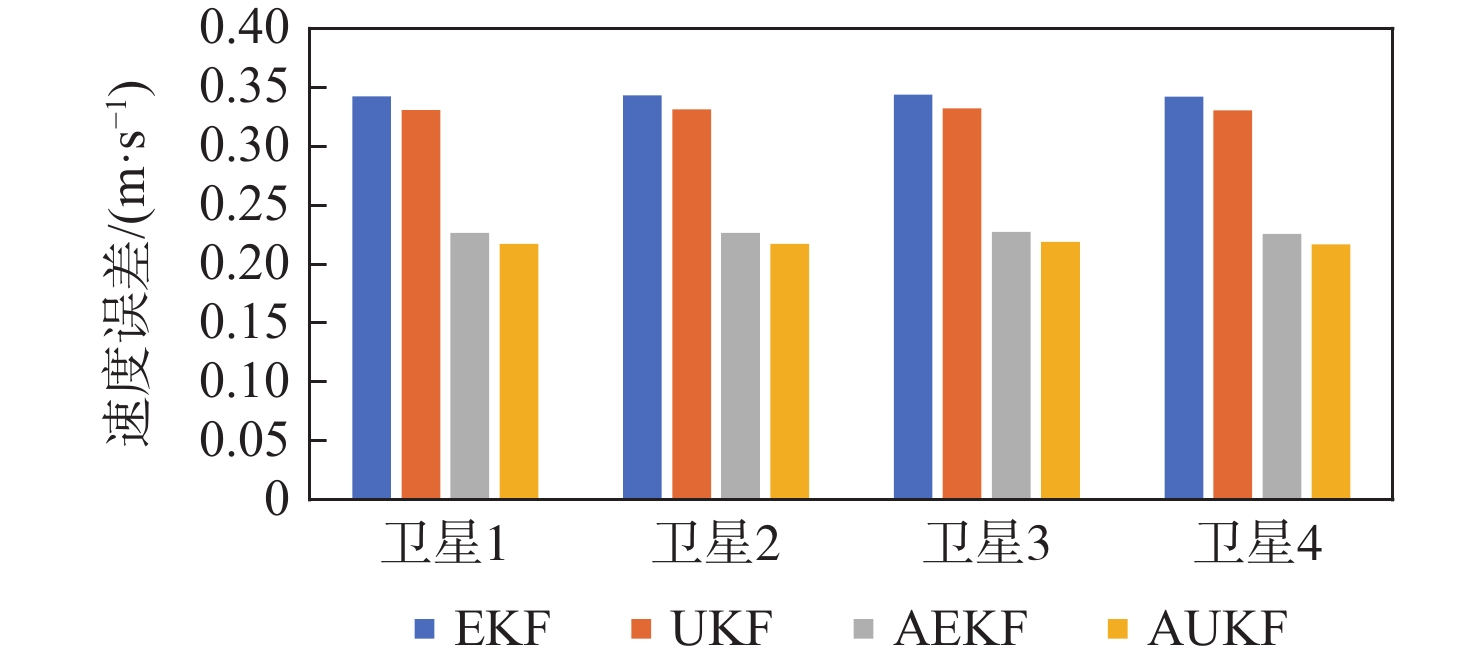
星座构型 滤波方法 位置误差/m 速度误差/(m·s−1) 低轨局域星座 UKF 272.74 0.332 3 AUKF 207.03 0.216 7 EKF 280.24 0.344 2 AEKF 215.21 0.227 6 中轨全球星座 UKF 50.01 0.012 0 AUKF 20.06 0.002 6 EKF 54.63 0.014 0 AEKF 29.58 0.005 3
下载: 导出CSV
表 3 不同算法的仿真耗时统计
Table 3. Simulation time statistics of different algorithms
滤波算法 仿真时长/s EKF 89.72 UKF 1 407.31 AEKF 94.21 AUKF 1 408.59
下载: 导出CSV
A1 不同滤波算法的导航误差统计
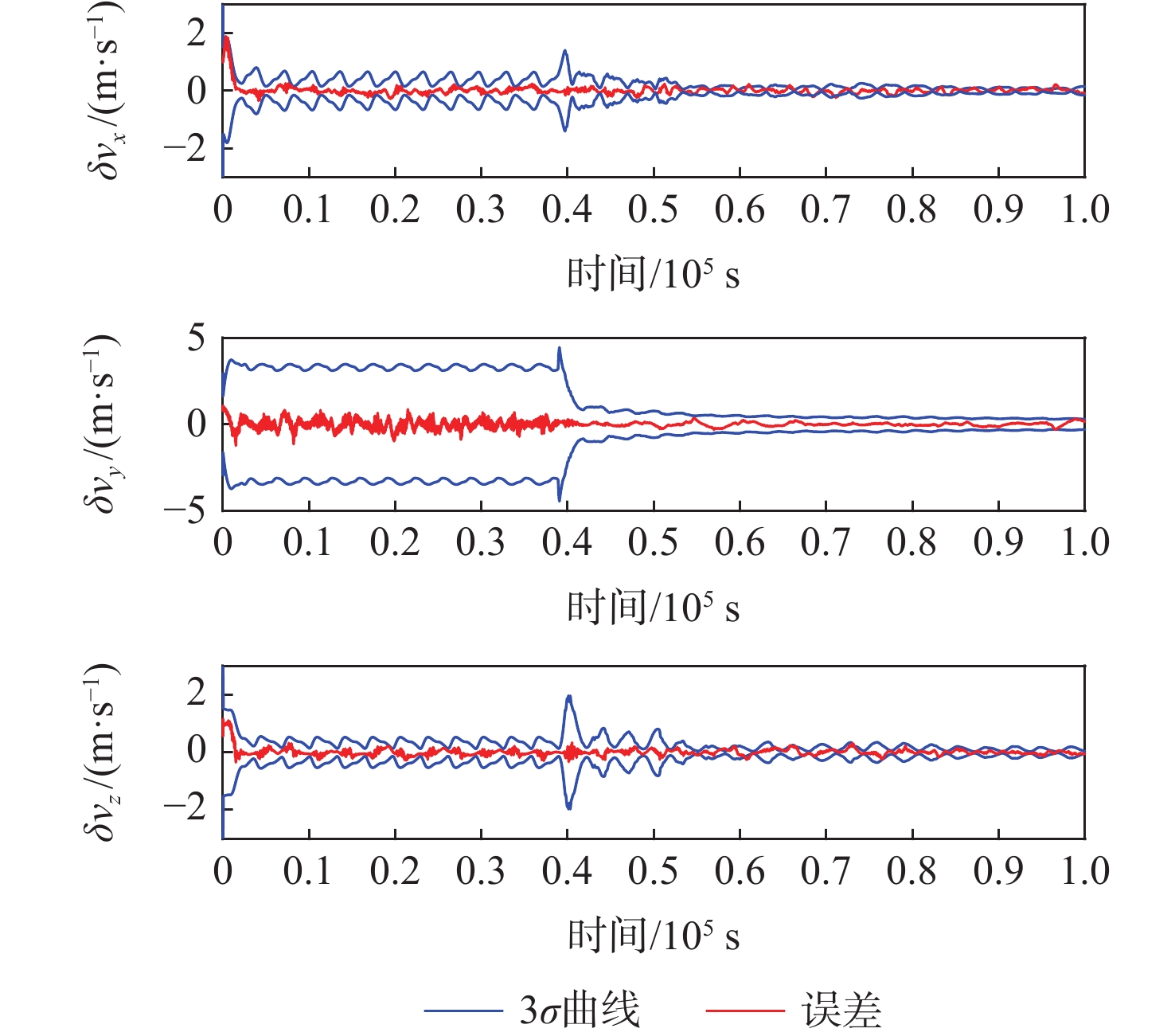
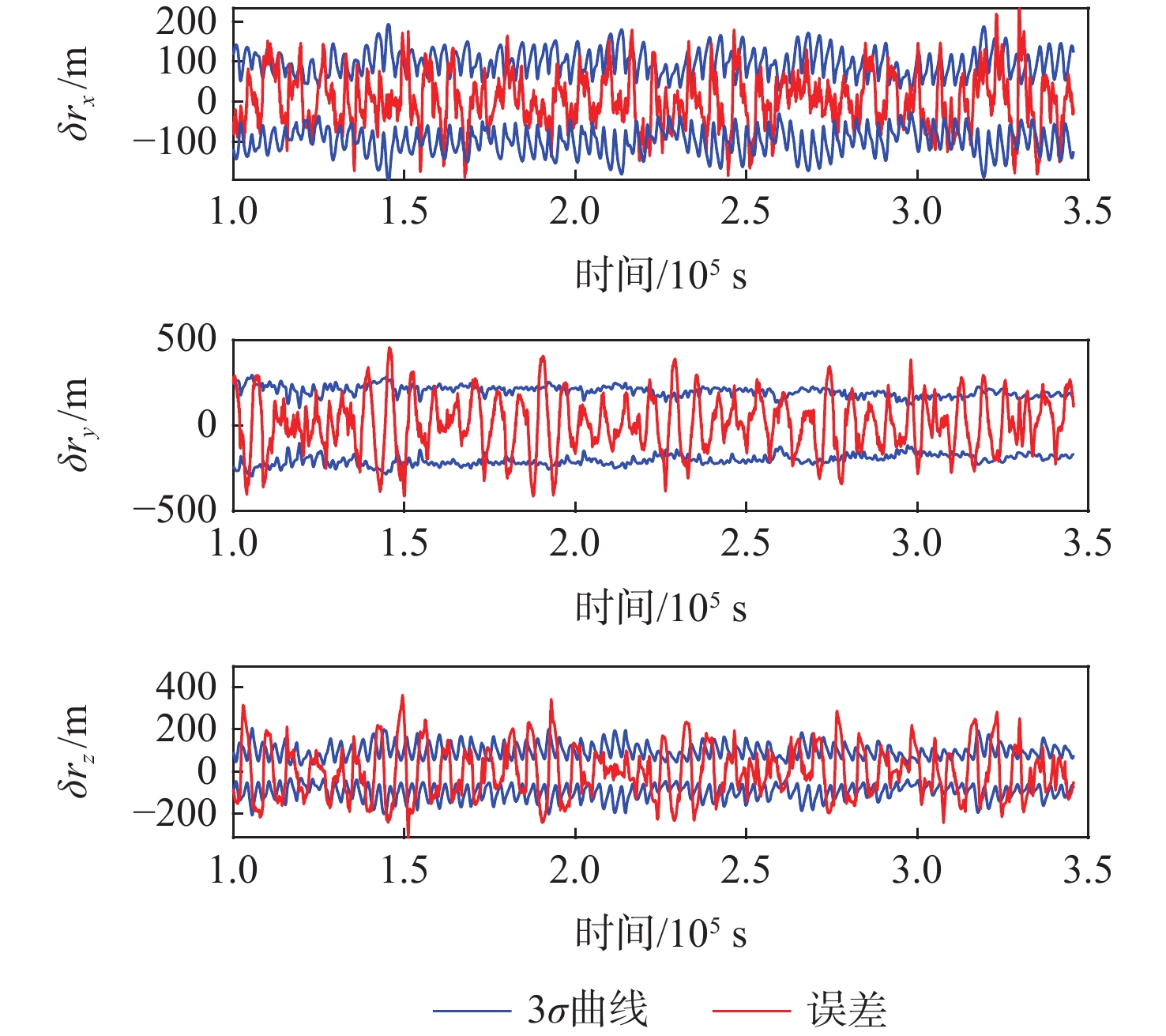
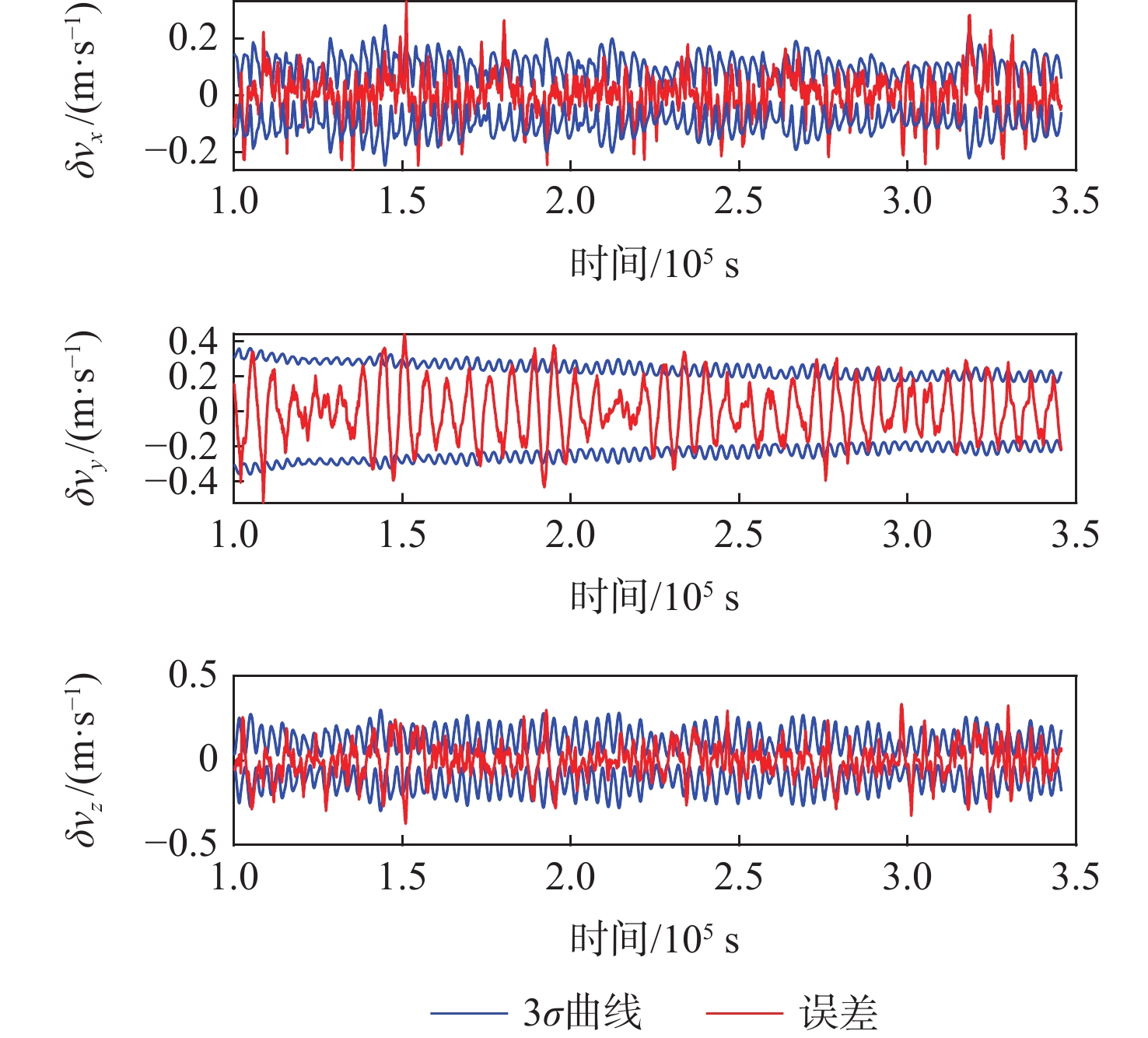
A1. Navigation error statistics under different filtering algorithms
卫星编号 滤波算法 $\delta {r_x}$/m $\delta {r_y}$/m $\delta {r_{\textit{z}}}$/m $\delta r$/m $\delta {v_x}$/(m·s−1) $\delta {v_y}$/(m·s−1) $\delta {v_{\textit{z}}}$/(m·s−1) $\delta v$/(m·s−1) 1 EKF 109.82 231.22 115.93 281.01 0.130 6 0.294 9 0.115 9 0.342 7 UKF 95.77 229.98 110.67 272.03 0.106 5 0.295 6 0.103 2 0.330 7 AEKF 80.54 166.61 109.83 215.19 0.085 3 0.183 9 0.100 4 0.226 4 AUKF 77.51 161.87 103.46 207.16 0.084 1 0.176 5 0.094 2 0.217 1 2 EKF 110.04 231.34 116.17 273.11 0.129 4 0.296 3 0.115 7 0.343 4 UKF 96.03 230.15 110.52 272.77 0.105 1 0.297 1 0.102 9 0.331 5 AEKF 80.50 166.79 109.42 215.11 0.084 0 0.184 6 0.100 4 0.226 3 AUKF 77.46 161.87 103.46 207.08 0.083 0 0.177 7 0.093 1 0.217 1 3 EKF 109.65 231.34 116.17 281.14 0.131 4 0.296 2 0.115 7 0.344 1 UKF 95.58 230.11 110.91 272.74 0.107 5 0.296 9 0.103 1 0.332 2 AEKF 80.51 166.60 110.09 215.31 0.086 1 0.184 7 0.101 4 0.227 6 AUKF 77.49 161.86 103.72 207.27 0.084 8 0.178 0 0.094 6 0.218 7 4 EKF 109.90 231.23 115.79 280.99 0.130 1 0.298 4 0.115 8 0.342 4 UKF 95.85 229.98 110.53 272.61 0.106 5 0.295 6 0.130 7 0.330 4 AEKF 80.52 166.59 109.60 215.06 0.084 8 0.183 8 0.099 9 0.225 7 AUKF 77.49 161.85 103.72 207.03 0.083 7 0.176 6 0.093 6 0.216 7
下载: 导出CSV
表 4 CRLB方差下界统计
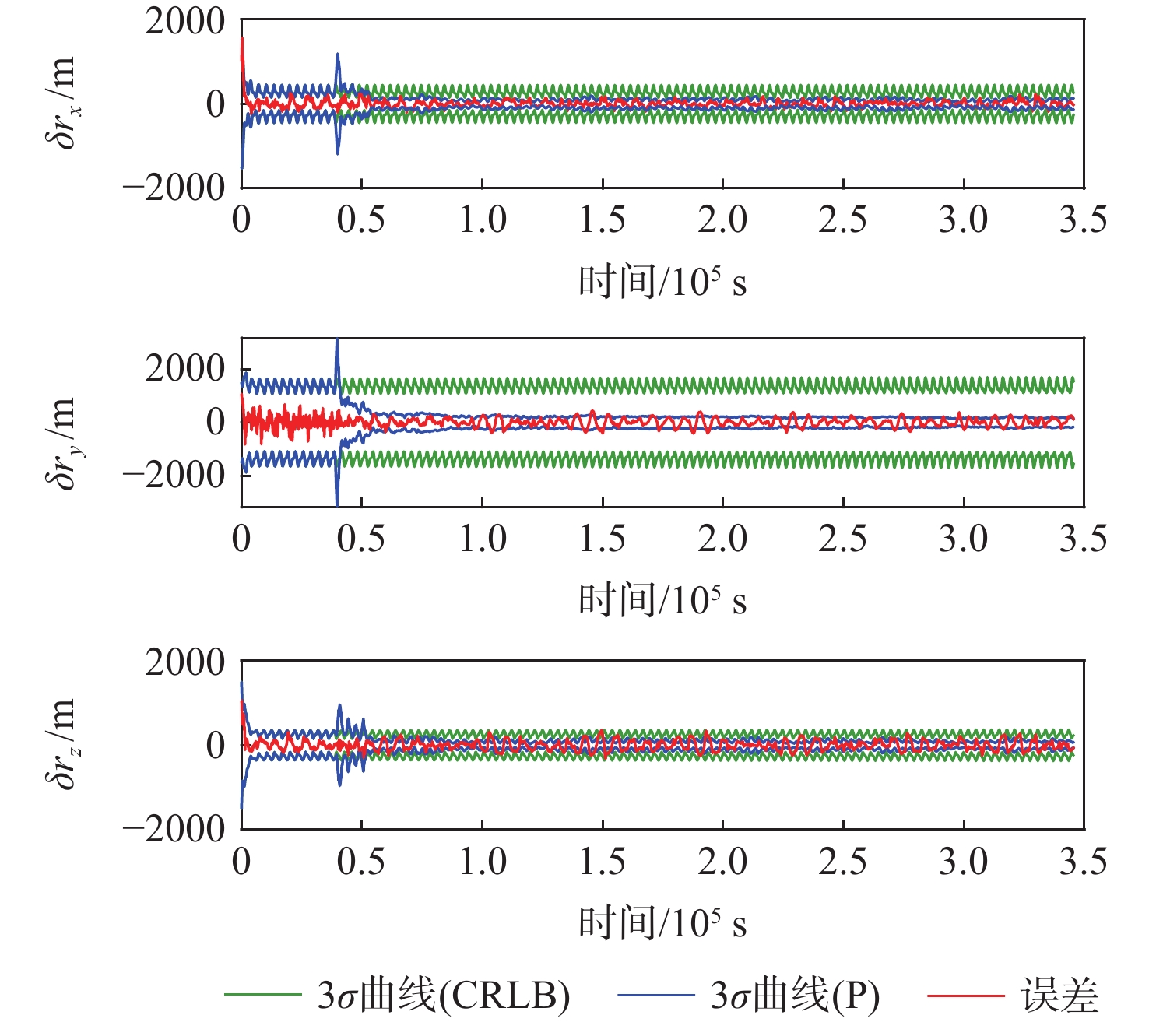
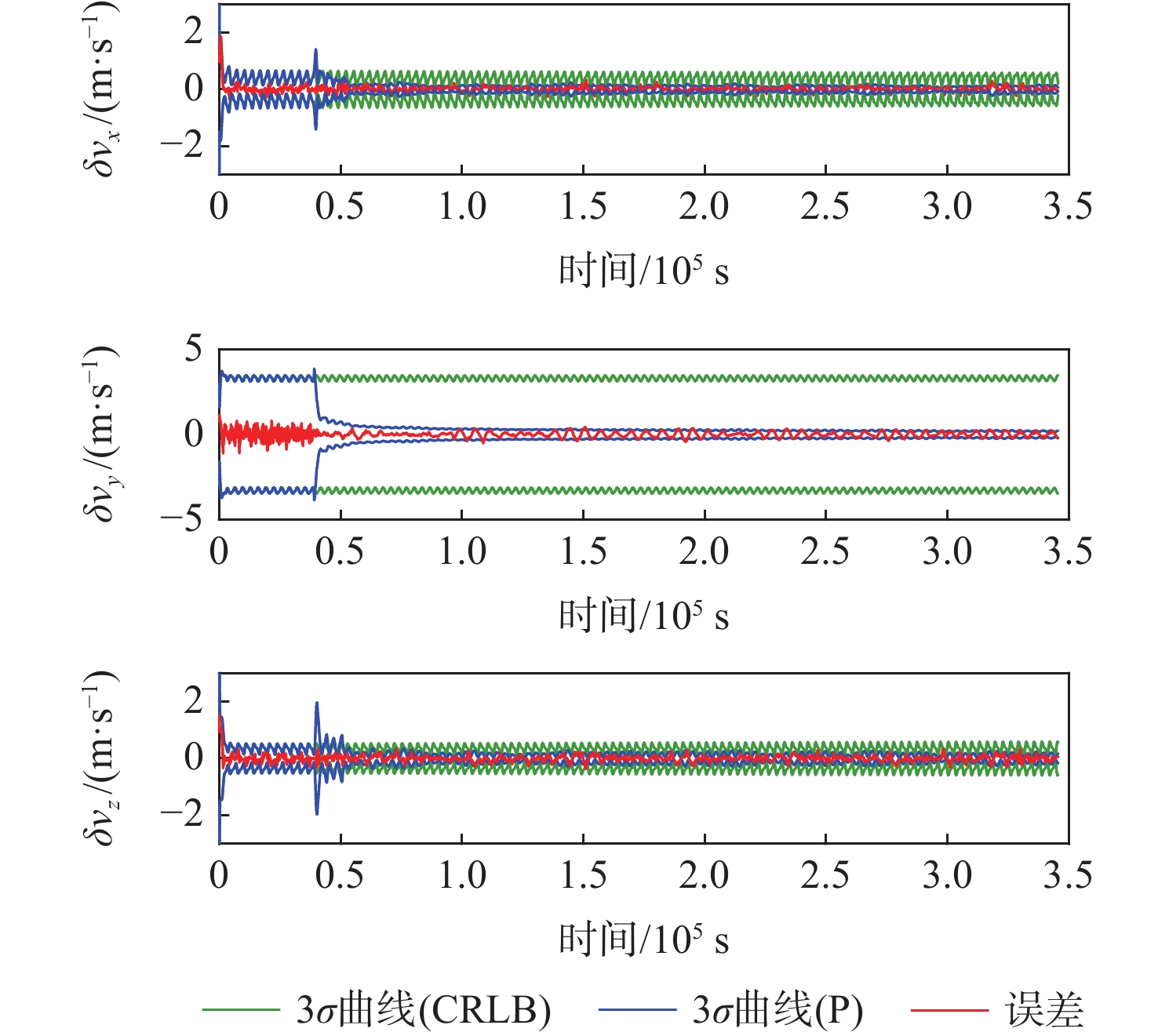
Table 4. CRLB statistics of variance
噪声
情况均值 $\delta {r_x}$/m $\delta {r_y}$/m $\delta {r_{\textit{z}}}$/m $\delta {v_x}$/(m·s−1) $\delta {v_y}$/(m·s−1) $\delta {v_{\textit{z}}}$/(m·s−1) 非理想 1$\sigma $ 96.22 456.01 89.08 0.132 2 1.100 8 0.120 8 3$\sigma $ 283.83 1 364.04 261.17 0.390 3 3.304 1 0.352 6 理想 1$\sigma $ 47.57 59.04 60.97 0.052 7 0.055 9 0.056 6 3$\sigma $ 142.70 177.11 182.90 0.158 2 0.167 7 0.169 8
下载: 导出CSV
-
[1] PSIAKI M L. Absolute orbit and gravity determination using relative position measurements between two satellites[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(5): 1285-1297. doi: 10.2514/1.47560 [2] KIHARA M, OKADA T. A satellite selection method and accuracy for the global positioning system[J]. Navigation, 1984, 31(1): 8-20. doi: 10.1002/j.2161-4296.1984.tb00856.x [3] GARCÍA-FERNÁNDEZ Á F, SVENSSON L. Gaussian MAP filtering using Kalman optimization[J]. IEEE Transactions on Automatic Control, 2015, 60(5): 1336-1349. doi: 10.1109/TAC.2014.2372909 [4] CHEN L, JIANG B W, LIU Y Q, et al. Application of adaptive EKF in real-time orbit determination[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(4): 187. doi: 10.1007/s40430-021-02867-z [5] XU Y, SHEN T, CHEN X Y, et al. Predictive adaptive Kalman filter and its application to INS/UWB-integrated human localization with missing UWB-based measurements[J]. International Journal of Automation and Computing, 2019, 16(5): 604-613. doi: 10.1007/s11633-018-1157-4 [6] CAO L, YANG W W, LI H N, et al. Robust double gain unscented Kalman filter for small satellite attitude estimation[J]. Advances in Space Research, 2017, 60(3): 499-512. doi: 10.1016/j.asr.2017.03.014 [7] LIU X H, GUAN J W, GAO X, et al. Adaptive robust unscented Kalman filter for power system dynamic state estimation[C]// 2021 40th Chinese Control Conference (CCC). Piscataway: IEEE Press, 2021: 6793-6798. [8] SHAN C H, ZHOU W D, YANG Y F, et al. Multi-fading factor and updated monitoring strategy adaptive Kalman filter-based variational Bayesian[J]. Sensors, 2020, 21(1): 198. doi: 10.3390/s21010198 [9] MEHRJOUYAN A, ALFI A. Robust adaptive unscented Kalman filter for bearings-only tracking in three dimensional case[J]. Applied Ocean Research, 2019, 87: 223-232. doi: 10.1016/j.apor.2019.01.034 [10] QI W J, SHENG Z B, WANG S G. Robust centralized fusion Kalman filters with uncertain noise variances[C]// 2019 Chinese Control and Decision Conference (CCDC). Piscataway: IEEE Press, 2019: 4028-4033. [11] ABDUL SALAM A O, SHERIFF R E, HU Y F, et al. Automatic modulation classification using interacting multiple model Kalman filter for channel estimation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(9): 8928-8939. [12] MALEKZADEH P, SALIMIBENI M, MOHAMMADI A, et al. MM-KTD: multiple model Kalman temporal differences for reinforcement learning[J]. IEEE Access, 2020, 8: 128716-128729. doi: 10.1109/ACCESS.2020.3007951 [13] XIONG K, WEI C L, ZHANG H Y. Parallel model adaptive Kalman filtering for autonomous navigation with line-of-sight measurements[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(11): 4017-4031. doi: 10.1177/0954410018813053 [14] KIUMARSI B, VAMVOUDAKIS K G, MODARES H, et al. Optimal and autonomous control using reinforcement learning: a survey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(6): 2042-2062. doi: 10.1109/TNNLS.2017.2773458 [15] XIONG K, WEI C L, ZHANG H Y. Q-learning for noise covariance adaptation in extended Kalman filter[J]. Asian Journal of Control, 2021, 23(4): 1803-1816. doi: 10.1002/asjc.2336 [16] PENG S M, CHEN C, SHI H B, et al. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator[J]. IEEE Access, 2017, 5: 13202-13212. doi: 10.1109/ACCESS.2017.2725301 [17] HAJIYEV C, SOKEN H E, GULER D C. Q-adaptation of SVD-aided UKF algorithm for nanosatellite attitude estimation[J]. IFAC-PapersOnLine, 2017, 50(1): 8273-8278. doi: 10.1016/j.ifacol.2017.08.1399 [18] SOKEN H E, HACIZADE C, SAKAI S I. Simultaneous adaptation of the process and measurement noise covariances for the UKF applied to nanosatellite attitude estimation[J]. IFAC Proceedings Volumes, 2014, 47(3): 5921-5926. doi: 10.3182/20140824-6-ZA-1003.00773 [19] HAVANGI R. Adaptive robust unscented Kalman filter with recursive least square for state of charge estimation of batteries[J]. Electrical Engineering, 2022, 104(2): 1001-1017. doi: 10.1007/s00202-021-01358-7 [20] 李瑞鹏. 基于测向测距的星座自主导航方法仿真研究[D]. 北京: 北京航空航天大学, 2018: 23-24.LI R P. Simulation Research on autonomous navigation method of constellation based on directions and ranging[D]. Beijing: Beihang University, 2018: 23-24(in Chinese). [21] 何丽娜. 不同摄动力对低中高轨航天器轨道的影响分析[J]. 大地测量与地球动力学, 2017, 37(11): 1156-1160,1165.HE L N. Perturbation forces analysis for spacecraft of different orbit altitudes[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1156-1160,1165 (in Chinese). [22] LIU F, LIU Y B, SUN X J, et al. A new multi-sensor hierarchical data fusion algorithm based on unscented Kalman filter for the attitude observation of the wave glider[J]. Applied Ocean Research, 2021, 109: 102562. doi: 10.1016/j.apor.2021.102562 -
下载:
点击查看大图
计量
- 文章访问数: 253
- HTML全文浏览量: 120
- PDF下载量: 3
- 被引次数: 0
