基于改进平衡优化算法的折叠翼飞行器自抗扰控制器设计

孟志鹏; 杨柳庆; 王波; 刘燕斌

doi:10.13700/j.bh.1001-5965.2022.0698

基于改进平衡优化算法的折叠翼飞行器自抗扰控制器设计

doi: 10.13700/j.bh.1001-5965.2022.0698

1.
军事科学院国防科技创新研究院，北京 100071
2.
南京航空航天大学无人机研究院，南京 210016
3.
南京航空航天大学航天学院，南京 210016

详细信息

通讯作者:
E-mail：yangliuqing@nuaa.edu.cn

中图分类号: V249.1
计量
- 文章访问数: 146
- HTML全文浏览量: 96
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-09
- 录用日期: 2022-09-08
- 网络出版日期: 2022-09-21
- 整期出版日期: 2024-08-28

ADRC design for folding wing vehicles based on improved equilibrium optimization algorithm

1.
National Innovation Institute of Defense Technology，Academy of Military Sciences，Beijing 100071，China
2.
Research Institute of Pilotless Aircraft，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China
3.
College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China

More Information

Corresponding author: E-mail：yangliuqing@nuaa.edu.cn

摘要

摘要:
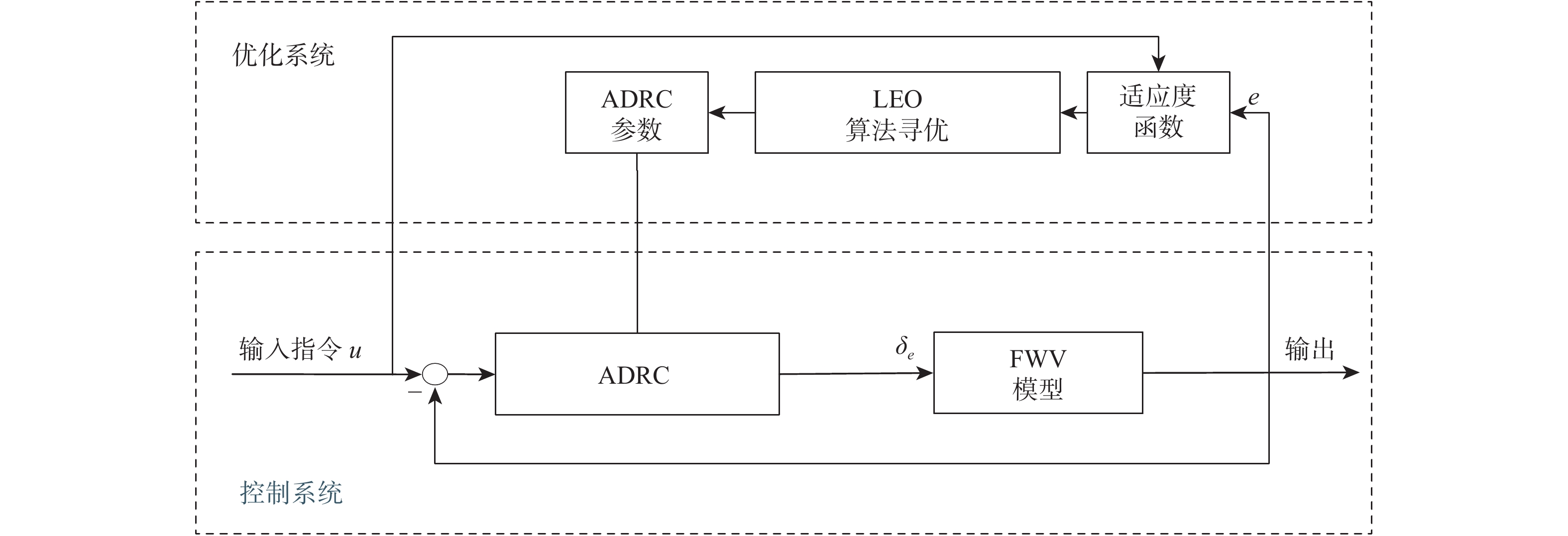
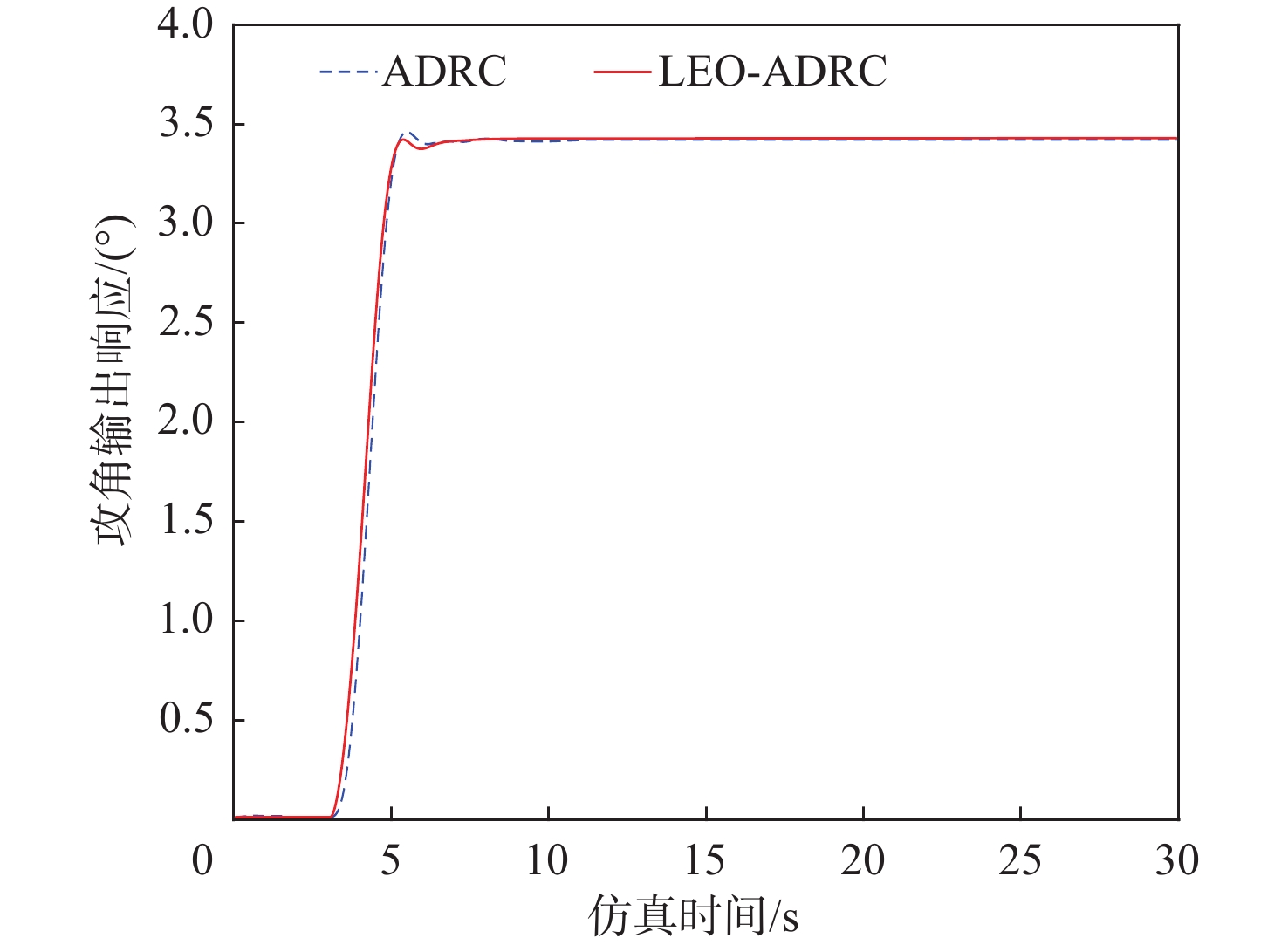
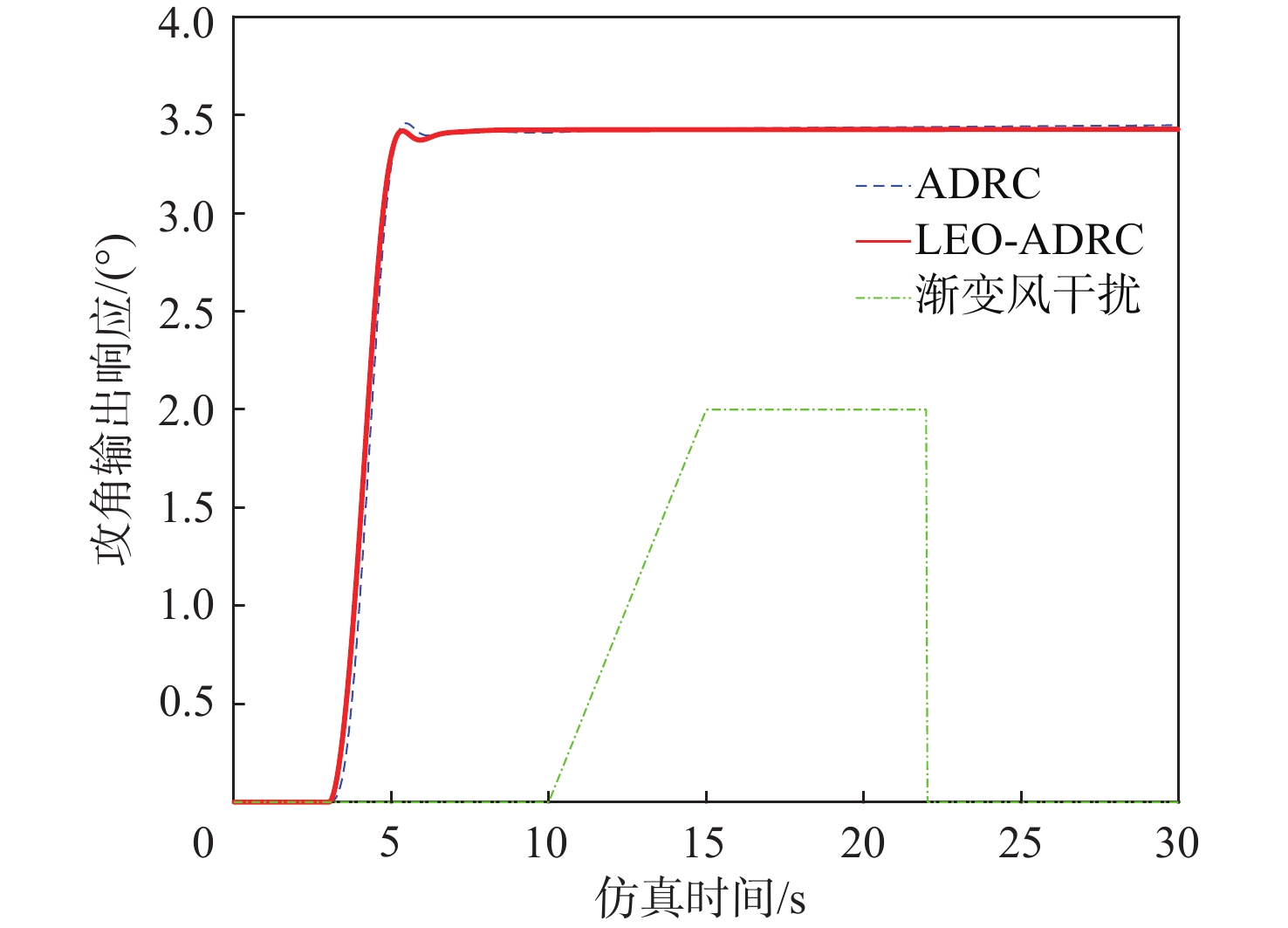
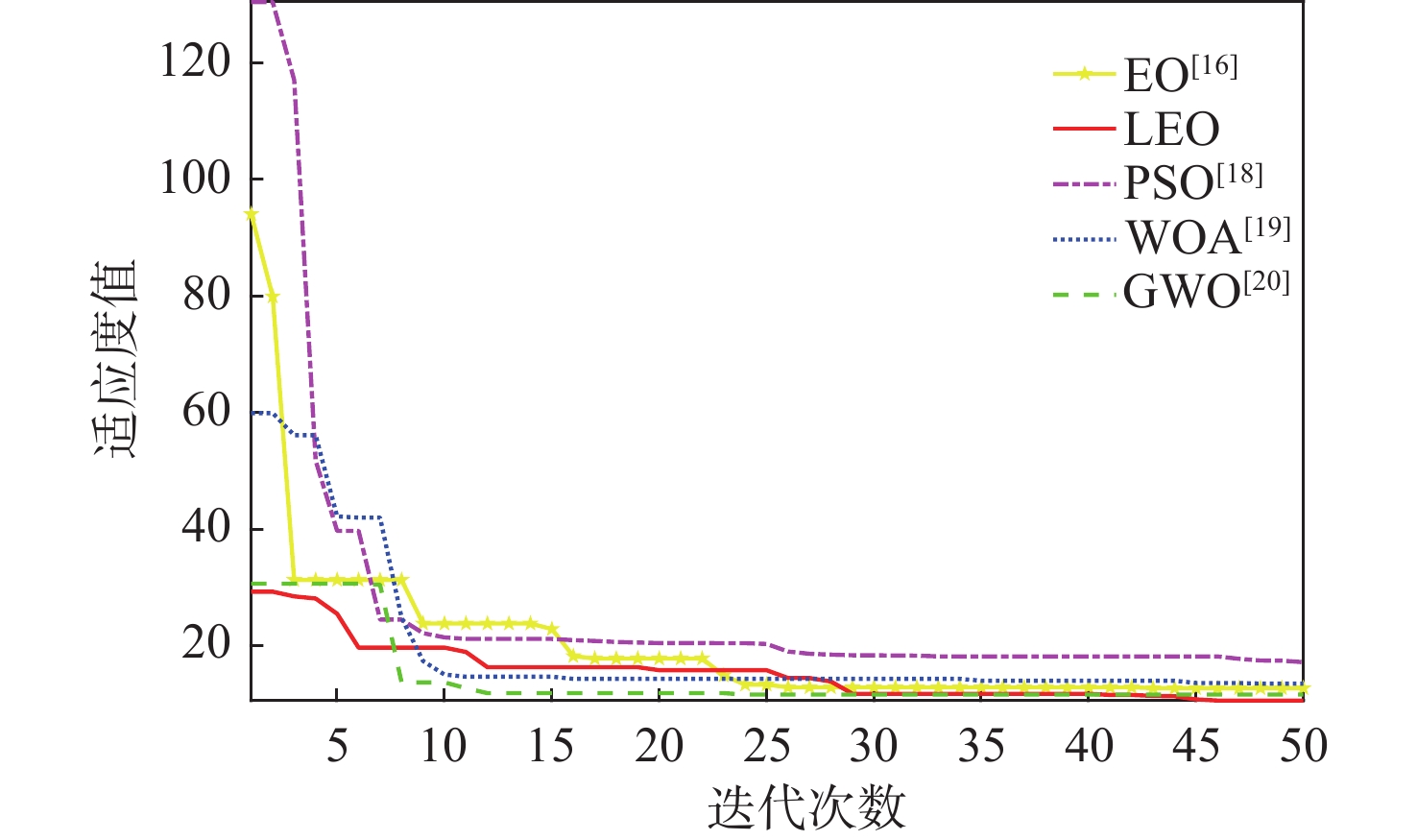
针对折叠翼飞行器（FWV）模型误差和抗扰动能力较差及自抗扰控制器（ADRC）人工参数整定难的问题，提出一种基于莱维飞行的改进平衡优化（LEO）算法。给出典型FWV动力学模型，基于ADRC结构设计一种FWV的姿态控制器；在此基础上用所提算法整定了ADRC参数，并从控制性能和抗干扰的角度对经参数优化后的ADRC和传统ADRC进行仿真对比；将所提算法与经典平衡优化算法、粒子群优化（PSO）算法等进行仿真对比。仿真结果表明：所提算法优化的控制器能提高FWV的控制精度和扰动抑制性能，验证了所提算法在解决ADRC参数优化问题时的优越性。对搭载优化后ADRC的样机进行实飞验证，结果表明：在风扰之下，FWV样机仍具有较好的飞行性能指标，进一步验证了所提算法优化的ADRC对FWV抗扰能力的提升。
- 折叠翼飞行器 /
- 改进平衡优化算法 /
- 莱维飞行 /
- 自抗扰控制器 /
- 姿态控制
Abstract:
In view of the modeling errors and poor anti-disturbance ability of folding wing vehicles (FWV) and the difficulty in manual parameter setting of active disturbance rejection controllers (ADRC), an optimization algorithm based on improved equilibrium optimizer based on Lévy（LEO）was proposed. A dynamics model of typical FWV was established, and an attitude controller for the FWV was designed based on the ADRC structure. The parameters of the ADRC were adjusted by the proposed algorithm, and a comparison between the optimized ADRC and the traditional ADRC by the simulation was made from the perspective of control performance and anti-disturbance. The proposed algorithm was compared with the classical equilibrium optimizer, particle swarm optimization (PSO) algorithm, and so on. The simulation results show that the controller optimized by the proposed algorithm can improve the control accuracy and disturbance suppression performance of FWV, and the superiority of the algorithm in the parameter optimization of ADRC was verified. The prototype equipped with the improved ADRC was verified in real flight. The results show that the FWV prototype still has a good flight performance index under wind disturbance, which further verifies that ADRC optimized by the proposed algorithm improves the anti-disturbance of FWV.
- folding wing vehicle /
- improved equilibrium optimization algorithm /
- Levy flight /
- active disturbance rejection controller /
- attitude control

HTML全文

图 1 FWV总体布局

Figure 1. Overall layout of FWV

下载: 全尺寸图片幻灯片

图 2 FWV操纵面

Figure 2. Control surface of FWV

下载: 全尺寸图片幻灯片

图 3 总体布置

Figure 3. General layout

下载: 全尺寸图片幻灯片

图 4 飞行器姿态控制器结构框图

Figure 4. Structure block diagram of attitude controller

下载: 全尺寸图片幻灯片

图 5 莱维飞行轨迹仿真

Figure 5. Simulation of Levy flight trajectory

下载: 全尺寸图片幻灯片

图 6 LEO算法流程图

Figure 6. Flow chart of LEO algorithm

下载: 全尺寸图片幻灯片

图 7 基于LEO算法的控制参数优化原理

Figure 7. Principle of control parameter optimization based on LEO algorithm

下载: 全尺寸图片幻灯片

图 8 攻角输出响应

Figure 8. Output response of angle of attack

下载: 全尺寸图片幻灯片

图 9 渐变风干扰下攻角跟踪曲线

Figure 9. Tracking curve of angle of attack under gradient disturbance

下载: 全尺寸图片幻灯片

图 10 适应度收敛曲线

Figure 10. Convergence curves of fitness

下载: 全尺寸图片幻灯片

图 11 攻角输出响应曲线

Figure 11. Output response curves of angle of attack

下载: 全尺寸图片幻灯片

图 12 适应度值分布箱线

Figure 12. Boxplot of fitness value distribution

下载: 全尺寸图片幻灯片

图 13 ${\beta _{01}}$箱线

Figure 13. Boxplot of ${\beta _{01}}$

下载: 全尺寸图片幻灯片

图 14 ${\beta _{02}}$箱线

Figure 14. Boxplot of ${\beta _{02}}$

下载: 全尺寸图片幻灯片

图 15 ${\beta _{03}}$箱线

Figure 15. Boxplot of ${\beta _{03}}$

下载: 全尺寸图片幻灯片

图 16 ${\beta _1}$箱线

Figure 16. Boxplot of ${\beta _1}$

下载: 全尺寸图片幻灯片

图 17 ${\beta _2}$箱线

Figure 17. Boxplot of ${\beta _2}$

下载: 全尺寸图片幻灯片

图 18 LEO-ESO观测下攻角通道扰动

Figure 18. Disturbance of angle of attack channel under LEO-ESO

下载: 全尺寸图片幻灯片

图 19 样机出筒

Figure 19. Prototype launched from cylinder

下载: 全尺寸图片幻灯片

图 20 样机实飞

Figure 20. Real flight drawing of prototype

下载: 全尺寸图片幻灯片

图 21 PID样机攻角响应

Figure 21. Angle of attack response of PID prototype

下载: 全尺寸图片幻灯片

图 22 LEO-ADRC样机攻角响应

Figure 22. Angle of attack response of LEO-ADRC prototype

下载: 全尺寸图片幻灯片

表 1 控制参数优化前后

Table 1. Control parameters before and after optimization

控制器	${\beta _{01}}$	${\beta _{02}}$	${\beta _{03}}$	${\beta _1}$	${\beta _2}$
ADRC	100.00	60 000.00	1 000 000.00	2 500.00	134.00
LEO算法优化后 ADRC	300.00	50 415.00	897 390.00	10 000	134

下载: 导出CSV

表 2 算法优化速度信息

Table 2. Speed informations of algorithm optimization

算法	平均优化时间/s
LEO	4.89
EO^[16]	8.12
PSO^[18]	5.64
GWO^[19]	4.95
WOA^[20]	6.31

下载: 导出CSV

参考文献(26)

[1]	HAAS F, GORB S, WOOTTON R J. Elastic joints in dermapteran hind wings: Materials and wing folding[J]. Arthropod Structure & Development, 2000, 29(2): 137-146.
[2]	何肇雄, 郑震山, 马东立, 等. 国外跨介质飞行器发展历程及启示[J]. 舰船科学技术, 2016, 38(9): 152-157. doi: 10.3404/j.issn.1672-7619.2016.05.032 HE Z X, ZHENG Z S, MA D L, et al. Development of foreign trans-media aircraft and its enlightenment to China[J]. Ship Science and Technology, 2016, 38(9): 152-157 (in Chinese). doi: 10.3404/j.issn.1672-7619.2016.05.032
[3]	杨立本, 章卫国, 黄得刚. 基于ADRC姿态解耦的四旋翼飞行器鲁棒轨迹跟踪[J]. 北京航空航天大学学报, 2015, 41(6): 1026-1033. YANG L B, ZHANG W G, HUANG D G. Robust trajectory tracking for quadrotor aircraft based on ADRC attitude decoupling control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1026-1033 (in Chinese).
[4]	石嘉, 裴忠才, 唐志勇, 等. 改进型自抗扰四旋翼无人机控制系统设计与实现[J]. 北京航空航天大学学报, 2021, 47(9): 1823-1831. SHI J, PEI Z C, TANG Z Y, et al. Design and realization of an improved active disturbance rejection quadrotor UAV control system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1823-1831 (in Chinese).
[5]	韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 197-270. HAN J Q. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 197-270 (in Chinese).
[6]	高志强. 自抗扰控制思想探究[J]. 控制理论与应用, 2013, 30(12): 1498-1510. doi: 10.7641/CTA.2013.31087 GAO Z Q. On the foundation of active disturbance rejection control[J]. Control Theory & Applications, 2013, 30(12): 1498-1510 (in Chinese). doi: 10.7641/CTA.2013.31087
[7]	韩京清. 从PID技术到“自抗扰控制” 技术[J]. 控制工程, 2002, 9(3): 13-18. doi: 10.3969/j.issn.1671-7848.2002.03.003 HAN J Q. From PID technique to active disturbances rejection control technique[J]. Basic Automation, 2002, 9(3): 13-18 (in Chinese). doi: 10.3969/j.issn.1671-7848.2002.03.003
[8]	王丽君, 李擎, 童朝南, 等. 时滞系统的自抗扰控制综述[J]. 控制理论与应用, 2013, 30(12): 1521-1533. doi: 10.7641/CTA.2013.31058 WANG L J, LI Q, TONG C N, et al. Overview of active disturbance rejection control for systems with time-delay[J]. Control Theory & Applications, 2013, 30(12): 1521-1533 (in Chinese). doi: 10.7641/CTA.2013.31058
[9]	李述清, 张胜修, 刘毅男, 等. 根据系统时间尺度整定自抗扰控制器参数[J]. 控制理论与应用, 2012, 29(1): 125-129. LI S Q, ZHANG S X, LIU Y N, et al. Parameter-tuning in active disturbance rejection controller using time scale[J]. Control Theory & Applications, 2012, 29(1): 125-129 (in Chinese).
[10]	李杰, 齐晓慧, 夏元清, 等. 线性/非线性自抗扰切换控制方法研究[J]. 自动化学报, 2016, 42(2): 202-212. LI J, QI X H, XIA Y Q, et al. On linear/nonlinear active disturbance rejection switching control[J]. Acta Automatica Sinica, 2016, 42(2): 202-212 (in Chinese).
[11]	LIANG S, RAJORA M, LIU X L, et al. Intelligent manufacturing systems: A review[J]. International Journal of Mechanical Engineering and Robotics Research, 2016, 7(2): 324-330. doi: 10.18178/ijmerr.7.3.324-330
[12]	LIU M, LIN R, YANG M, et al. Active disturbance rejection motion control of spherical robot with parameter tuning[J]. Industrial Robot, 2022, 49(2): 332-343. doi: 10.1108/IR-05-2021-0099
[13]	KANG C H, WANG S Q, REN W J, et al. Optimization design and application of active disturbance rejection controller based on intelligent algorithm[J]. IEEE Access, 2019, 7: 59862-59870. doi: 10.1109/ACCESS.2019.2909087
[14]	WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. doi: 10.1109/4235.585893
[15]	KAMARUZAMAN A F, ZAIN A M, YUSUF S M, et al. Levy flight algorithm for optimization problems - a literature review[J]. Applied Mechanics and Materials, 2013, 421: 496-501. doi: 10.4028/www.scientific.net/AMM.421.496
[16]	李守玉, 何庆, 陈俊. 改进平衡优化器算法在约束优化问题中的应用[J/OL]. 计算机科学与探索, 2021: 1-14 [2022-07-09]. https://kns.cnki.net/kcms/detail/11.5602.TP.20210901.1435.002.html. LI S Y, HE Q, CHEN J. Application of improved equilibrium optimizer algorithm to constrained optimization problems[J/OL]. Journal of Frontiers of Computer Science and Technology, 2021: 1-14 [2022-07-09]. https://kns.cnki.net/kcms/detail/11.5602.TP.20210901.1435.002.html (in Chinese).
[17]	杨柳庆, 杨婷婷, 王鹏飞, 等. 一种基于莱维飞行的新型改进平衡全局优化算法[J]. 宇航计测技术, 2020, 40(5): 62-69. doi: 10.12060/j.issn.1000-7202.2020.05.10 YANG L Q, YANG T T, WANG P F, et al. A new improved equilibrium global optimization algorithm based on Lévy flight[J]. Journal of Astronautic Metrology and Measurement, 2020, 40(5): 62-69 (in Chinese). doi: 10.12060/j.issn.1000-7202.2020.05.10
[18]	MARINI F, WALCZAK B. Particle swarm optimization (PSO): A tutorial[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153-165.
[19]	MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[20]	SAREMI S, MIRJALILI S Z, MIRJALILI S M. Evolutionary population dynamics and grey wolf optimizer[J]. Neural Computing and Applications, 2015, 26(5): 1257-1263.
[21]	唐志勇, 马福源, 裴忠才. 四旋翼的改进PSO-RBF神经网络自适应滑模控制[J]. 北京航空航天大学学报, 2023, 49(7): 1563-1572. TANG Z Y, MA F Y, PEI Z C. Improved PSO-RBF neural network adaptive sliding mode control for quadrotor systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7): 1563-1572 (in Chinese).
[22]	CHE J F, LI D H, JI Y H, et al. Attitude control for a quadrotor base on ADRC with GSO parameter optimization[C]//Proceedings of the Chinese Control and Decision Conference. Piscataway: IEEE Press, 2018: 1364-1369.
[23]	ALJARAH I, FARIS H, MIRJALILI S. Optimizing connection weights in neural networks using the whale optimization algorithm[J]. Soft Computing, 2018, 22(1): 1-15. doi: 10.1007/s00500-016-2442-1
[24]	费伦, 段海滨, 徐小斌, 等. 基于变权重变异鸽群优化的无人机空中加油自抗扰控制器设计[J]. 航空学报, 2020, 41(1): 323490. FEI L, DUAN H B, XU X B, et al. ADRC controller design for UAV based on variable weighted mutant pigeon inspired optimization[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(1): 323490 (in Chinese).
[25]	杜作义, 马乐瑶. 基于Matlab/simulink的风速仿真研究[J]. 中国西部科技, 2013, 12(12): 46-47. doi: 10.3969/j.issn.1671-6396.2013.12.024 DU Z Y, MA L Y. Wind speed simulation based on matlab/simulink[J]. Science and Technology of West China, 2013, 12(12): 46-47 (in Chinese). doi: 10.3969/j.issn.1671-6396.2013.12.024
[26]	范培蕾, 张晓今, 杨涛. 高超声速飞行试验风场建模与仿真分析[J]. 战术导弹技术, 2009(2): 76-82. doi: 10.3969/j.issn.1009-1300.2009.02.018 FAN P L, ZHANG X J, YANG T. Analyses of high altitude wind model of hypersonic vehicle test[J]. Tactical Missile Technology March, 2009(2): 76-82(in Chinese). doi: 10.3969/j.issn.1009-1300.2009.02.018