点接触共轭渐开线蜗杆副啮合理论及性能分析

任雯; 李杰; 王天羽; 李海涛

doi:10.13700/j.bh.1001-5965.2022.0778

点接触共轭渐开线蜗杆副啮合理论及性能分析

doi: 10.13700/j.bh.1001-5965.2022.0778

任雯¹,
李杰^{1, 2},
王天羽^{1, 2},
李海涛^{1, 2, ,}

1.
中国农业大学工学院，北京 100083
2.
中国农业大学机械工程训练中心，北京 100083

基金项目: 直升机传动技术国家重点实验室基金(HTL-O-19G02)

详细信息

通讯作者:
E-mail：h.li@cau.edu.cn

中图分类号: TH132.4
计量
- 文章访问数: 226
- HTML全文浏览量: 92
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-14
- 录用日期: 2022-11-04
- 网络出版日期: 2023-01-10
- 整期出版日期: 2024-10-31

Meshing theory and performance analysis of point-contact conjugate involute worm gear pair

REN Wen¹,
LI Jie^{1, 2},
WANG Tianyu^{1, 2},
LI Haitao^{1, 2
, ,}

1.
College of Engineering，China Agricultural University，Beijing 100083，China
2.
Mechanical Engineering Training Center，China Agricultural University，Beijing 100083，China

Funds: Fund of National Key Laboratory of Science and Technology on Helicopter Transmission (HTL-O-19G02)

More Information

Corresponding author: E-mail：h.li@cau.edu.cn

摘要

摘要:
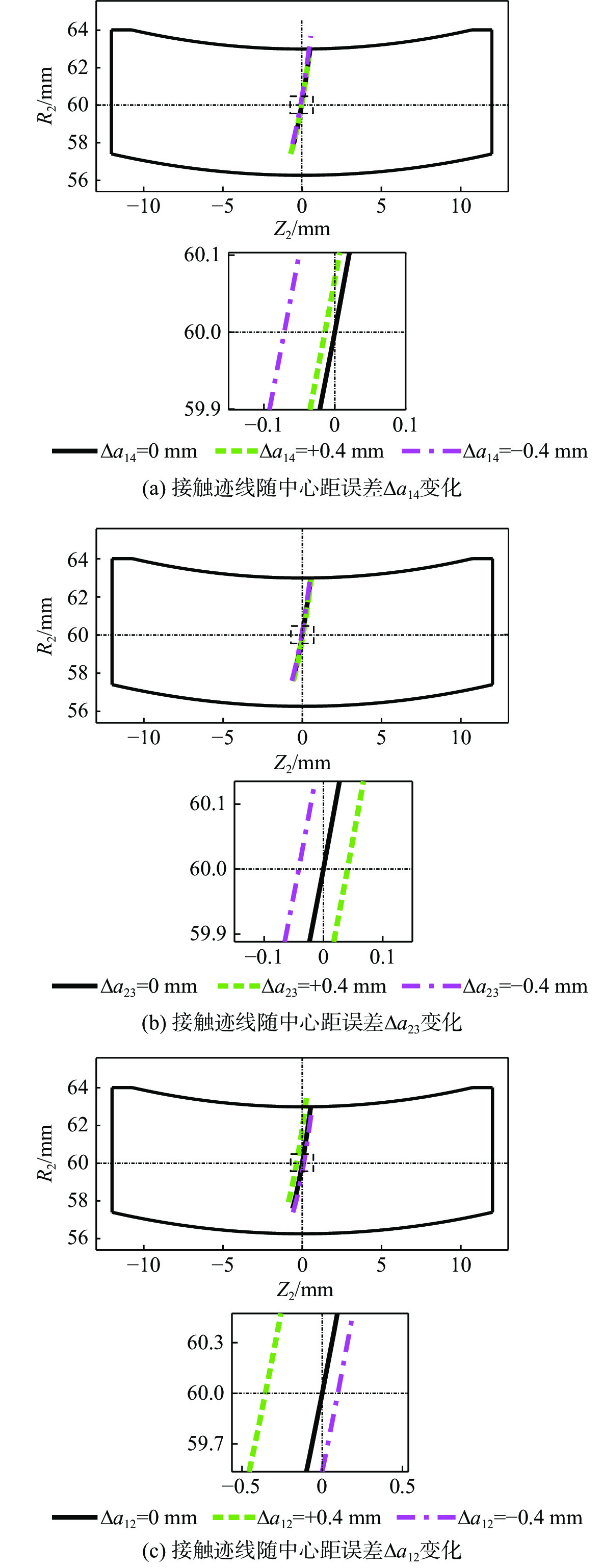
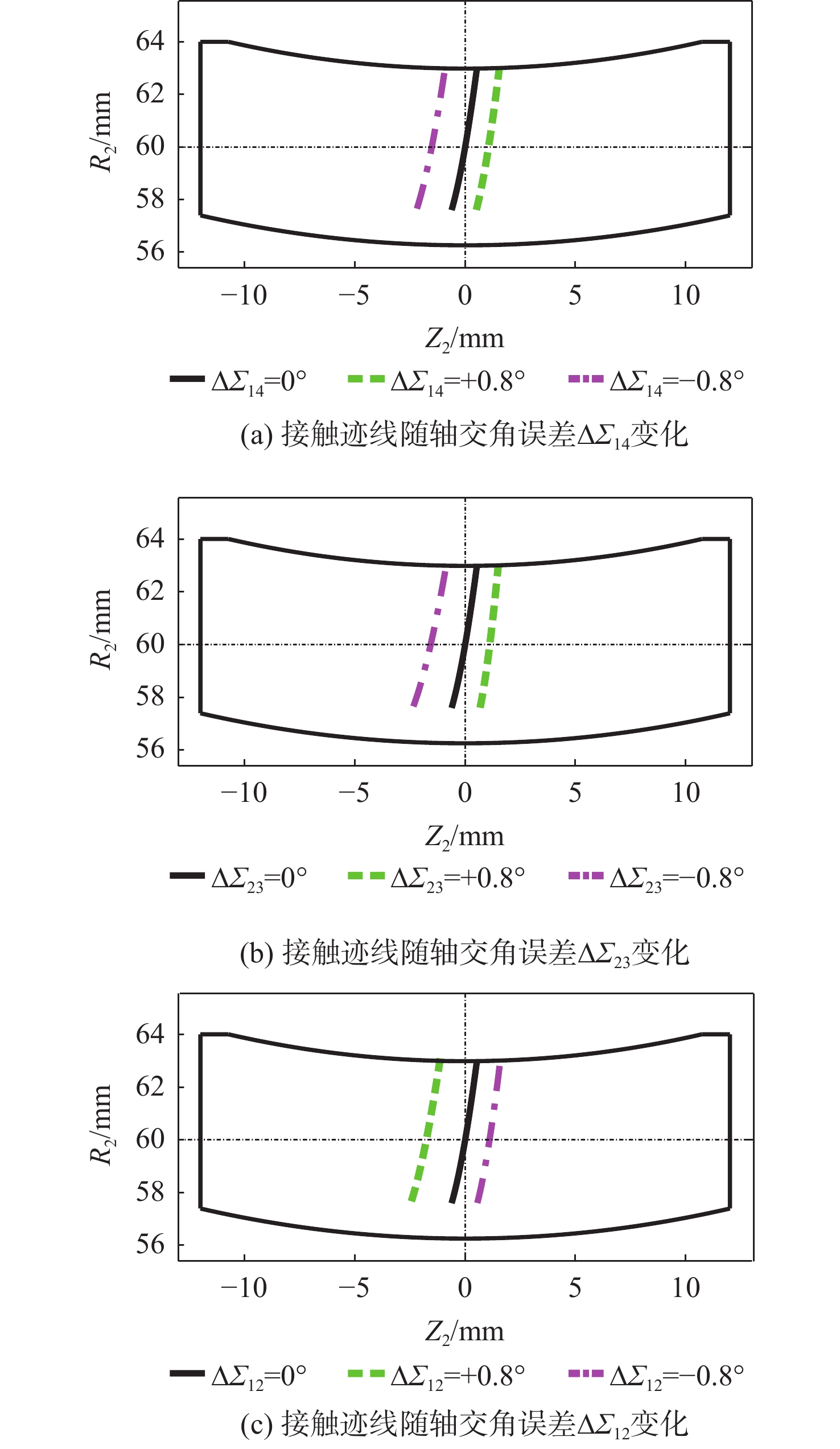
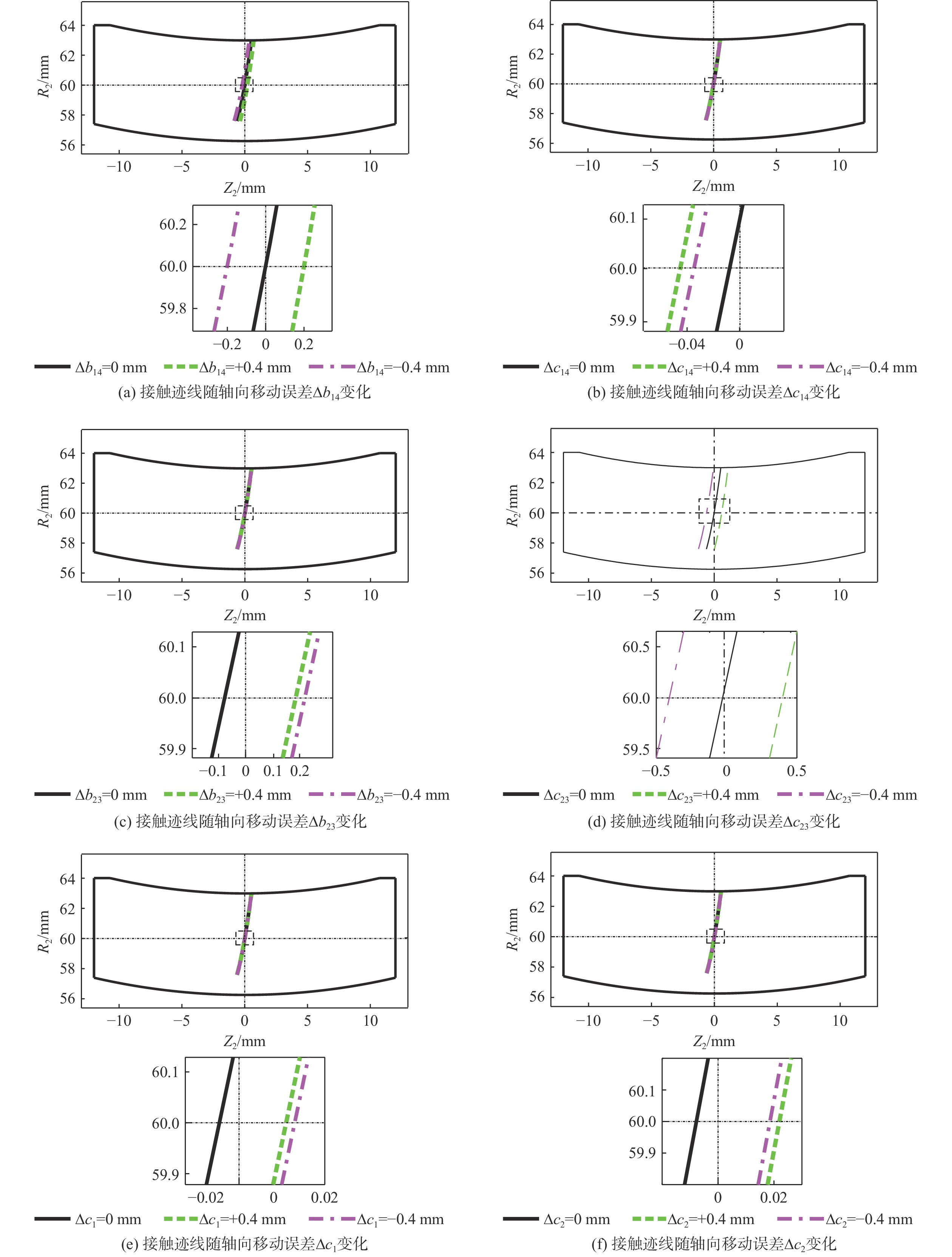
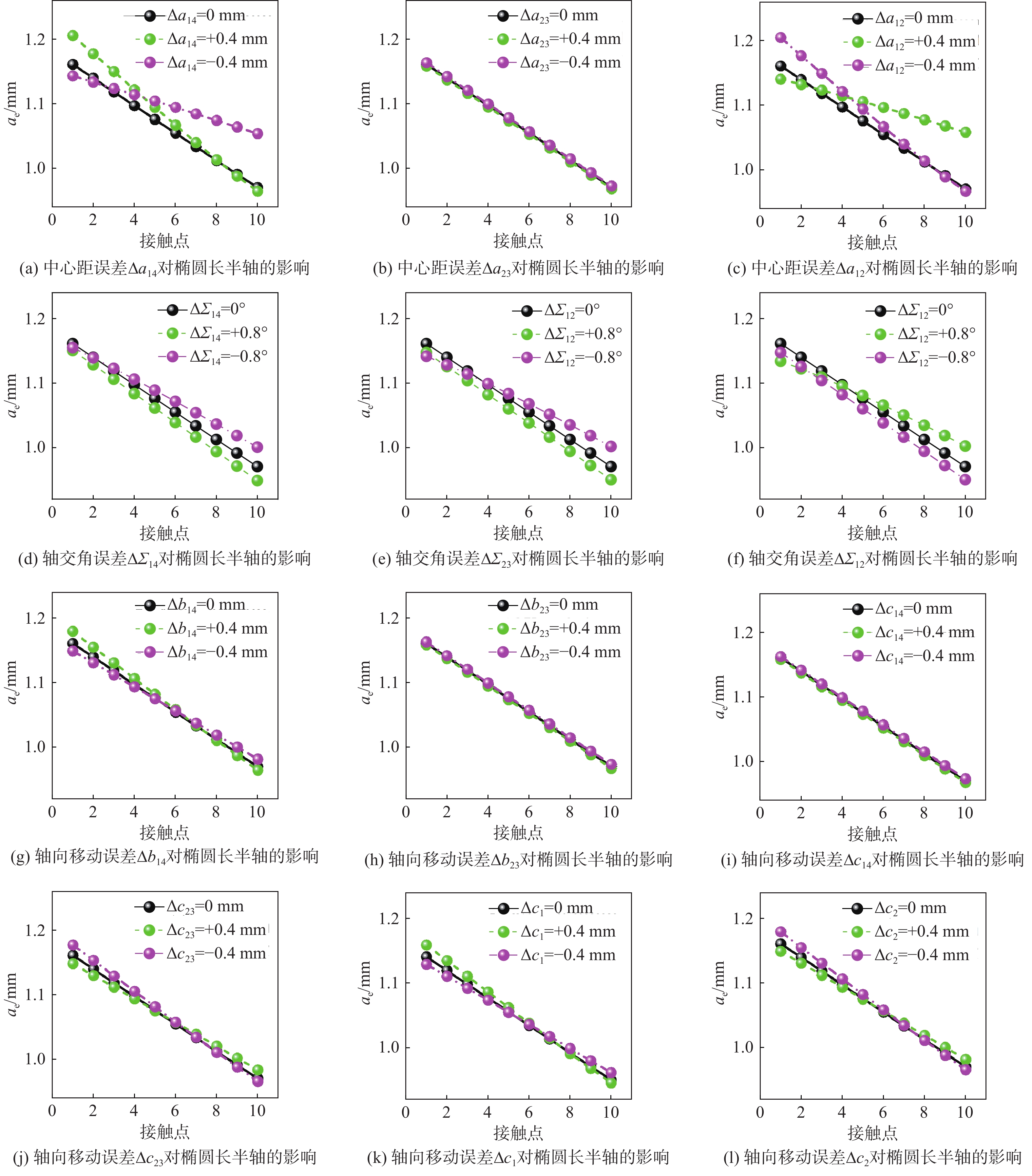
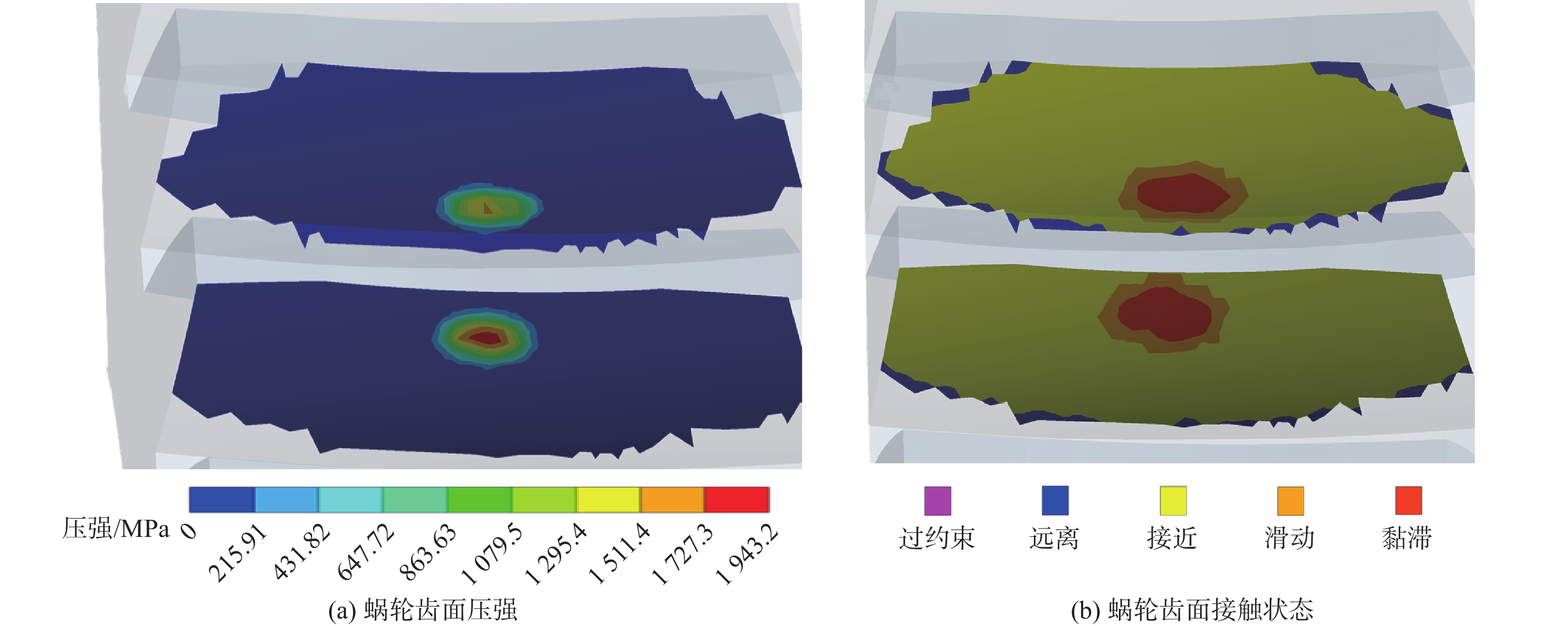
点接触共轭渐开线蜗杆传动可以降低蜗杆副对制造、装配等误差的敏感性，并能保证传动精度。基于微分几何和齿轮啮合原理，构建了含有制造和安装误差的点接触共轭渐开线蜗杆传动数学模型，研究了螺旋角、模数、压力角等主要设计参数对啮合性能的影响规律，并进行了传动副对制造和安装误差敏感性的研究。通过仿真实验验证了接触区的分布情况。研究结果表明，含有制造和安装误差时，传动副的瞬时传动比恒定；选取适中的螺旋角、较小的模数及较小的压力角会增大接触区的面积，提高传动副的重合度；传动副对制造和安装误差均不敏感，但应尽量减小或避免制造和安装轴交角造成的误差。通过仿真分析得到接触区和重合度与理论计算结果一致，验证了所提理论的正确性。
- 点接触 /
- 共轭 /
- 渐开线蜗杆 /
- 啮合性能 /
- 误差分析
Abstract:
Point-contact conjugate involute worm drive can reduce the sensitivity of the worm gear pair to manufacturing and assembly errors and ensure transmission accuracy. On the basis of differential geometry and gear meshing theory, this paper constructed a mathematical model of point-contact conjugate involute worm drive containing manufacturing and assembly errors, studied the influence of main design parameters such as helix angle, modulus, and pressure angle on the meshing performance, and analyzed the sensitivity of the worm gear pair to manufacturing and assembly errors. Finally, the distribution of the contact area was verified through simulation. The results show that the instantaneous drive ratio of the worm gear pair remains constant with manufacturing and assembly errors. The selection of a moderate helix angle, a small modulus, and a small pressure angle will increase the contact area and raise the contact ratio of the worm gear pair. The worm gear pair is insensitive to manufacturing and assembly errors, but the manufacturing and assembly errors of crossed axis angle should be minimized or avoided. The contact area and contact ratio obtained from the simulation analysis agree with the theoretical calculations, verifying the correctness of the theory.
- point contact /
- conjugate /
- involute worm /
- meshing performance /
- error analysis

HTML全文

图 1 双自由度展成渐开线蜗杆坐标系

Figure 1. Coordinate system of generation of involute worm with two degrees of freedom

下载: 全尺寸图片幻灯片

图 2 单自由度展成蜗轮坐标系

Figure 2. Coordinate system of generation of worm gear with single degree of freedom

下载: 全尺寸图片幻灯片

图 3 点接触共轭渐开线蜗杆副坐标系

Figure 3. Coordinate system of point-contact conjugate involute worm gear pair

下载: 全尺寸图片幻灯片

图 4 接触迹线与接触区随螺旋角的变化情况

Figure 4. Variation of contact line and area with helix angle

下载: 全尺寸图片幻灯片

图 5 螺旋角对椭圆长轴和重合度的影响

Figure 5. Influence of helix angle on major axis of ellipse and contact ratio

下载: 全尺寸图片幻灯片

图 6 接触迹线与接触区随模数的变化情况

Figure 6. Variation of contact line and area with modulus

下载: 全尺寸图片幻灯片

图 7 模数对椭圆长轴和重合度的影响

Figure 7. Influence of modulus on major axis of ellipse and contact ratio

下载: 全尺寸图片幻灯片

图 8 接触迹线与接触区随压力角的变化情况

Figure 8. Variation of contact line and area with pressure angle

下载: 全尺寸图片幻灯片

图 9 压力角对椭圆长轴和重合度的影响

Figure 9. Influence of pressure angle on major axis of ellipse and contact ratio

下载: 全尺寸图片幻灯片

图 10 接触迹线随中心距误差的变化情况

Figure 10. Variation of contact line with center distance error

下载: 全尺寸图片幻灯片

图 11 接触迹线随轴交角误差的变化情况

Figure 11. Variation of contact line with crossed axis angle error

下载: 全尺寸图片幻灯片

图 12 接触迹线随轴向移动误差的变化情况

Figure 12. Variation of contact line with axial movement error

下载: 全尺寸图片幻灯片

图 13 误差对椭圆长半轴的影响

Figure 13. Influence of error on major axis of ellipse

下载: 全尺寸图片幻灯片

图 14 点接触共轭渐开线蜗杆副三维模型

Figure 14. Three-dimensional model of point-contact conjugate involute worm gear pair

下载: 全尺寸图片幻灯片

图 15 蜗轮齿面接触压强及状态

Figure 15. Contact pressure and state of worm gear tooth surface

下载: 全尺寸图片幻灯片

图 16 安装误差对蜗轮齿面压强的影响

Figure 16. Influence of error on pressure of worm gear tooth surface

下载: 全尺寸图片幻灯片

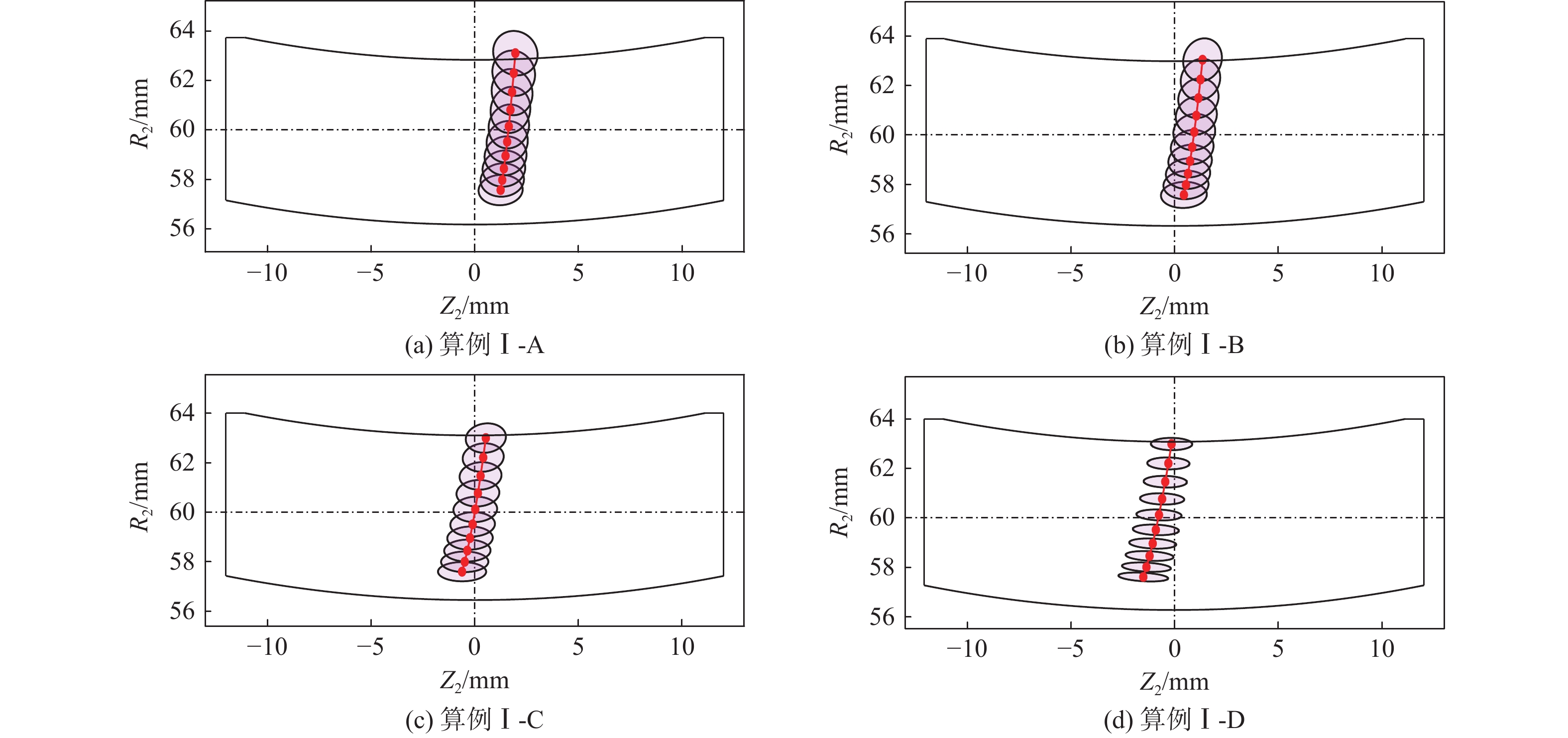
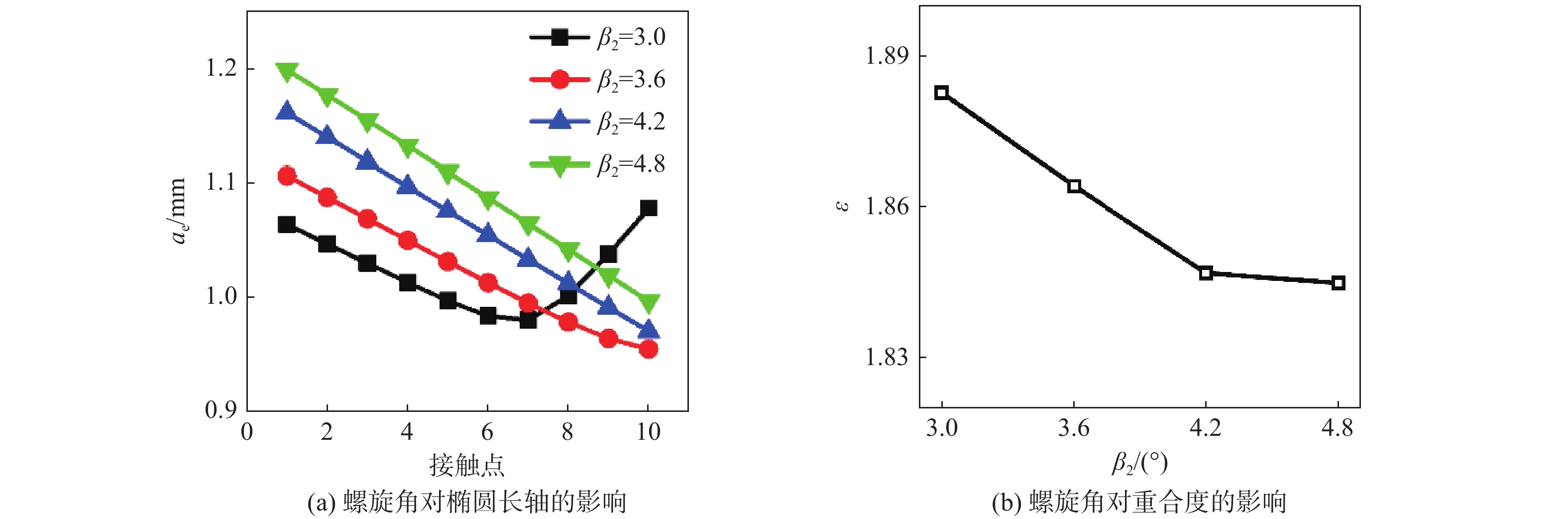
表 1 螺旋角几何参数

Table 1. Geometric parameters of helix angle

算例	螺旋角β₂/（°）
算例Ⅰ-A	3.0
算例Ⅰ-B	3.6
算例Ⅰ-C	4.2
算例Ⅰ-D	4.8

下载: 导出CSV

表 2 模数几何参数

Table 2. Geometric parameters of modulus

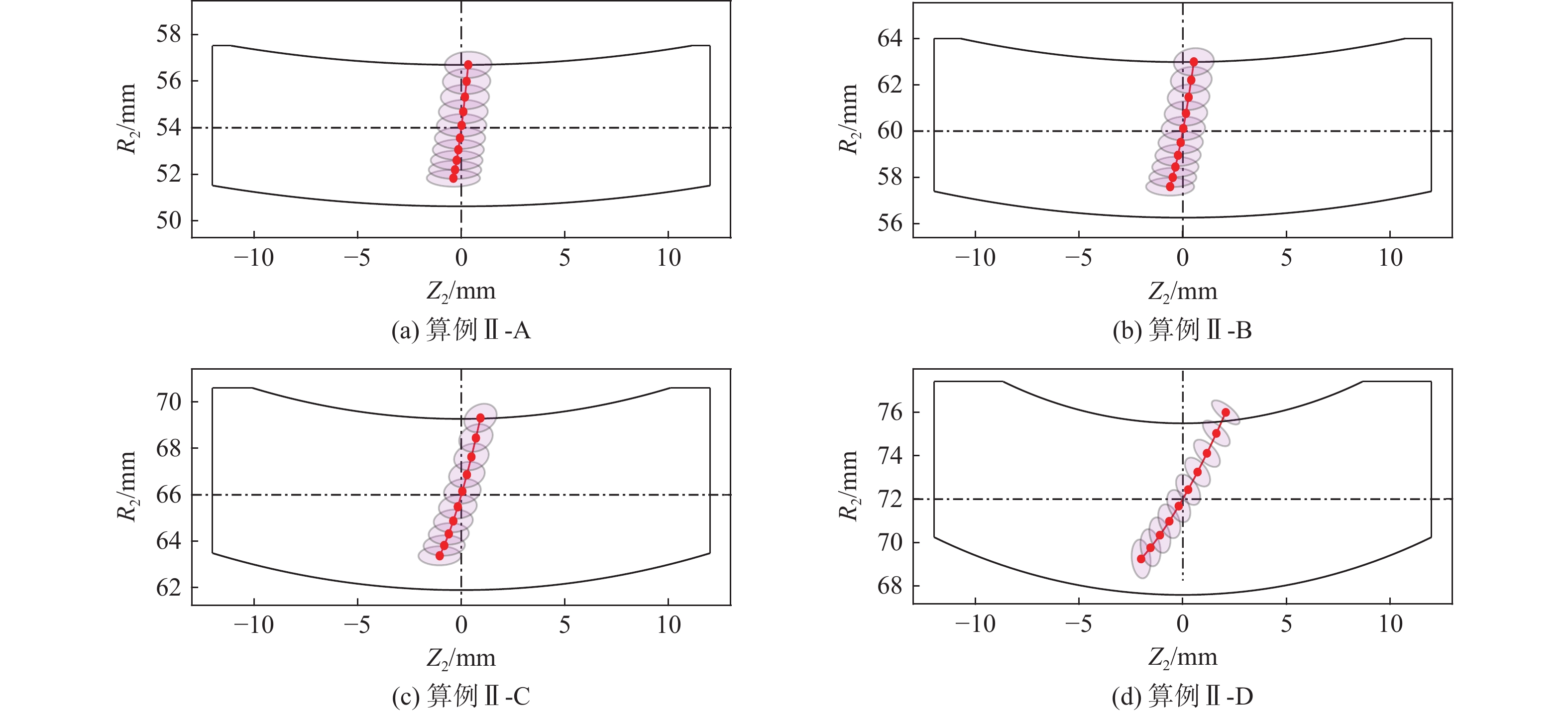
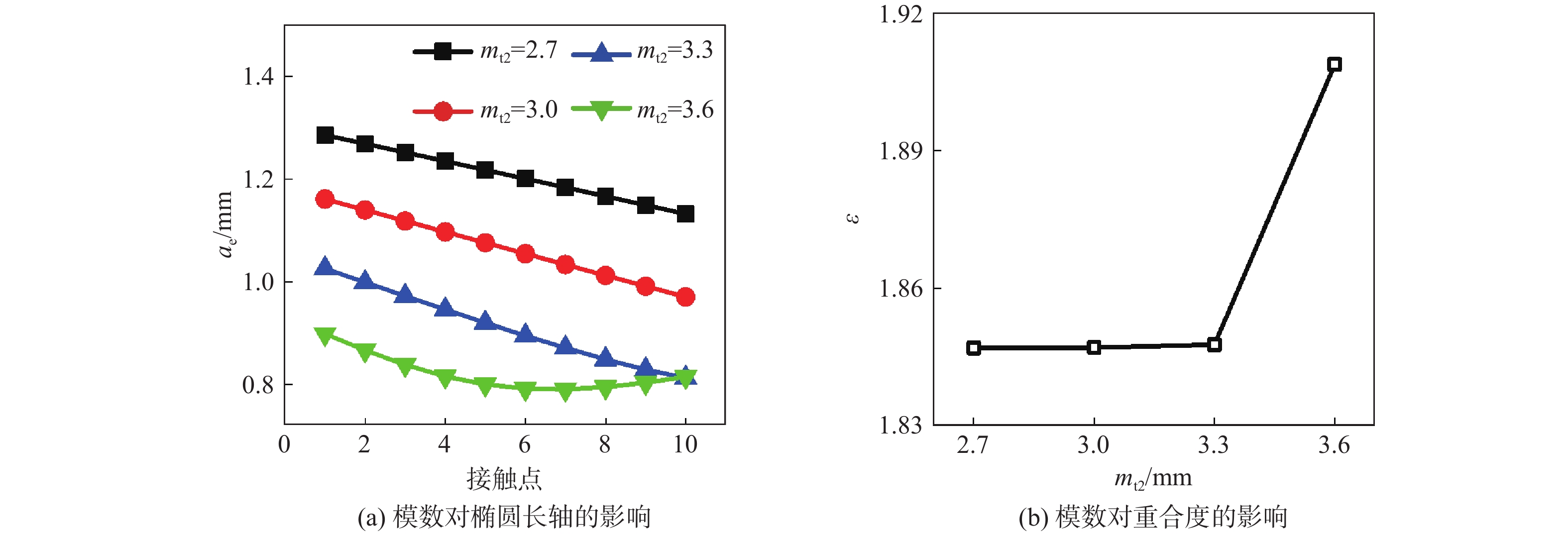
算例	端面模数m_t2/ mm
算例Ⅱ-A	2.7
算例Ⅱ-B	3.0
算例Ⅱ-C	3.3
算例Ⅱ-D	3.6

下载: 导出CSV

表 3 压力角几何参数

Table 3. Geometric parameters of pressure angle

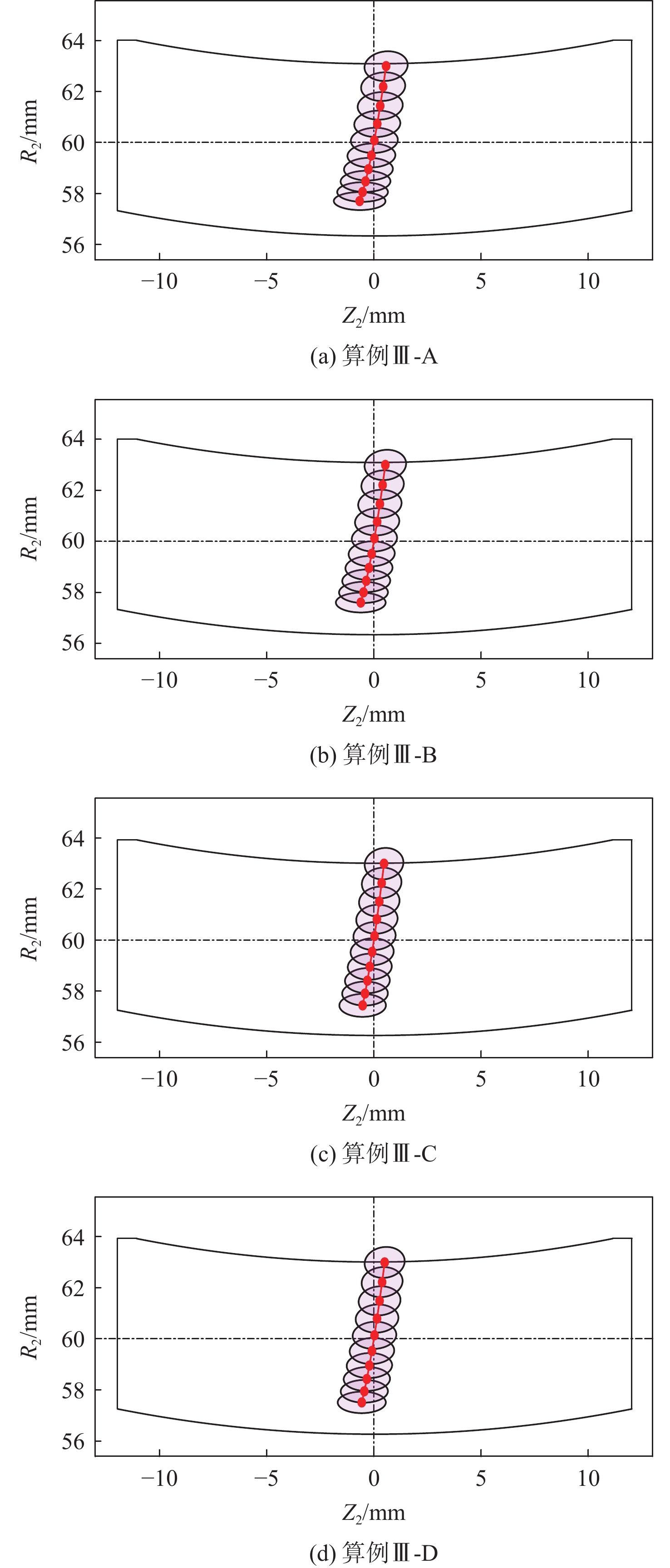
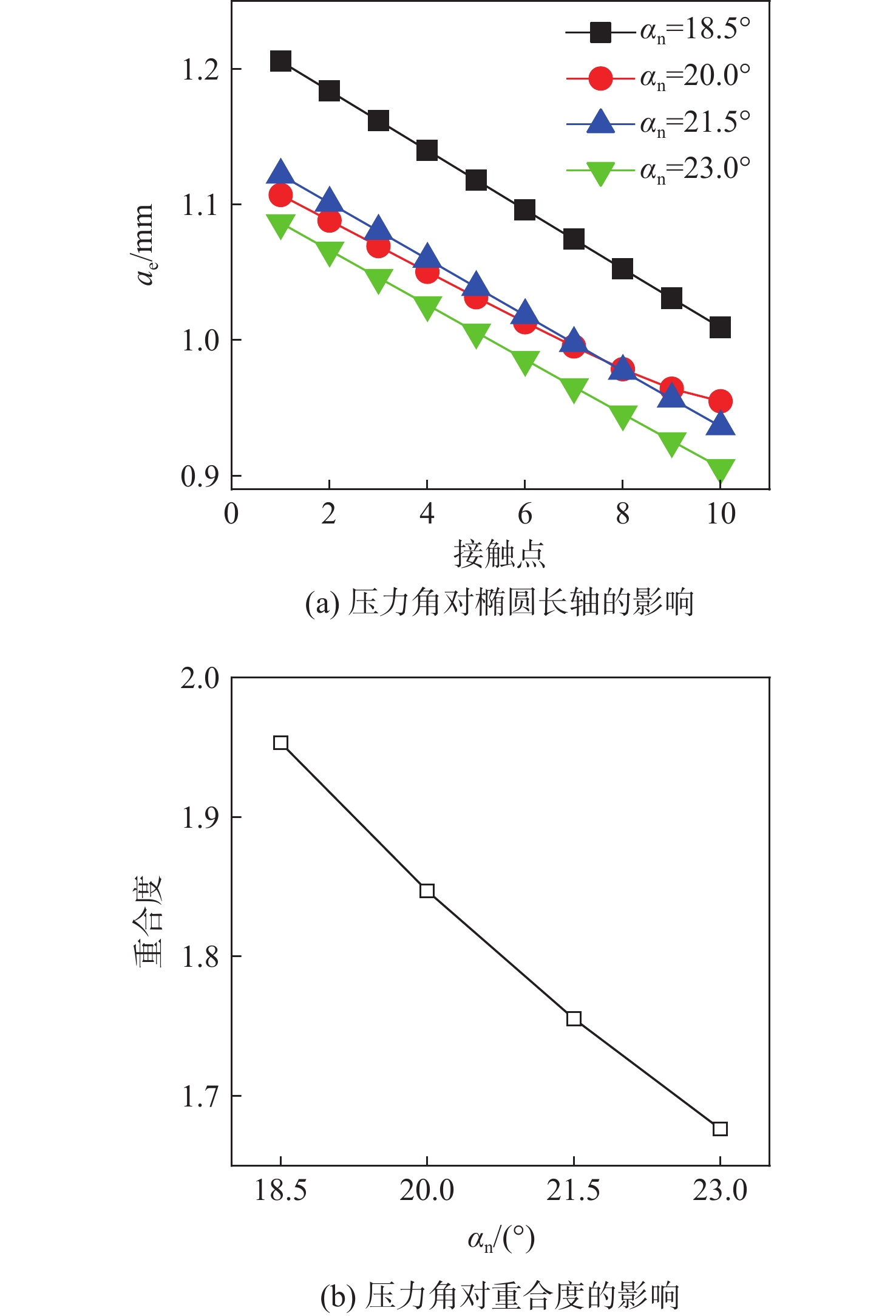
算例	压力角α_n/（°）
算例Ⅲ-A	18.5
算例Ⅲ-B	20.0
算例Ⅲ-C	21.5
算例Ⅲ-D	23.0

下载: 导出CSV

表 4 误差几何参数

Table 4. Geometric parameters of errors

参数	误差值	参数	误差值
∆a₁₄/mm	±0.4	∆Σ₁₄/(°)	±0.8
∆a₂₃/mm	±0.4	∆Σ₂₃/(°)	±0.8
∆a₁₂/mm	±0.4	∆Σ₁₂/(°)	±0.8
∆b₁₄/mm	±0.4	∆c₁₄/mm	±0.4
∆b₂₃/mm	±0.4	∆c₂₃/mm	±0.4
∆c₁/mm	±0.4	∆c₂/mm	±0.4

下载: 导出CSV

参考文献(22)

[1]	王树人, 刘平娟. 圆柱蜗杆传动啮合原理[M]. 天津: 天津科学技术出版社, 1982. WANG S R, LIU P J. Meshing principle of cylindrical worm drive[M]. Tianjin: Tianjin Scientific & Technical Publishers, 1982 (in Chinese).
[2]	LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. 2nd ed. New York: Cambridge University Press, 2004.
[3]	吴鸿业, 张亚雄, 齐麟. 蜗杆传动设计[M]. 北京: 机械工业出版社, 1986. WU H Y, ZHANG Y X, QI L. Worm drive design[M]. Beijing: China Machine Press, 1986(in Chinese).
[4]	申永胜. 机械原理教程[M]. 2版. 北京: 清华大学出版社, 2005: 162-165. SHEN Y S. Theory of machines and mechanisms[M]. 2nd ed. Beijing: Tsinghua University Press, 2005: 162-165(in Chinese).
[5]	田培棠. 齿轮刀具设计与选用手册[M]. 北京: 国防工业出版社, 2011: 73-77. TIAN P T. Handbook of gear cutter design and selection[M]. Beijing: National Defense Industry Press, 2011: 73-77(in Chinese).
[6]	彭泽良. 渐开线圆柱蜗杆传动承载啮合理论与实验研究[D]. 重庆: 重庆大学, 2003: 34-39. PENG Z L. Theoretical and experimental research on loaded meshing of involute cylinder worm-drive[D]. Chongqing: Chongqing University, 2003: 34-39(in Chinese).
[7]	赵迪, 方舟, 范庆明, 等. 渐开线蜗轮蜗杆参数化设计及装配误差分析[J]. 西安工业大学学报, 2019, 39(2): 152-158. ZHAO D, FANG Z, FAN Q M, et al. Parametric design and assembly error analysis of an involute worm gear[J]. Journal of Xi’an Technological University, 2019, 39(2): 152-158(in Chinese).
[8]	沈谦. 点接触圆柱蜗杆传动的设计原理[J]. 南京航空航天大学学报, 1991, 23(2): 48-54. SHEN Q. A design principle of cylindrical worm drive with point contact tooth surface[J]. Journal of Nanjing University of Aeronautics & Astronautics, 1991, 23(2): 48-54(in Chinese).
[9]	苏代忠, 陈兵奎, 秦大同, 等. 失配渐开线圆柱蜗杆传动的弹性啮合分析、加工仿真及相关技术的理论与试验研究[J]. 机械工程学报, 2002, 38(增刊1): 56-60. SU D Z, CHEN B K, QIN D T, et al. Elastic meshing analysis, machining simulation and theoretical and experimental research on related technologies of mismatched involute cylindrical worm drive[J]. Chinese Journal of Mechanical Engineering, 2002, 38(Sup 1): 56-60(in Chinese).
[10]	YE X X, CHEN Y H, LU B B, et al. Study on a novel backlash-adjustable worm drive via the involute helical beveloid gear meshing with dual-lead involute cylindrical worm[J]. Mechanism and Machine Theory, 2022, 167: 104466. doi: 10.1016/j.mechmachtheory.2021.104466
[11]	SIMON V. Load distribution in cylindrical worm gears[J]. Journal of Mechanical Design, 2003, 125(2): 356-364. doi: 10.1115/1.1561043
[12]	SIMON V. The influence of gear hobbing on worm gear characteristics[J]. Journal of Manufacturing Science and Engineering, 2007, 129(5): 919-925. doi: 10.1115/1.2752524
[13]	SIMON V. Computer aided loaded tooth contact analysis in cylindrical worm gears[J]. Journal of Mechanical Design, 2005, 127(5): 973-981. doi: 10.1115/1.1904050
[14]	秦大同, 张光辉, 加藤正名. 失配点啮合环面蜗杆传动的研究[J]. 机械工程学报, 1995, 31(3): 79-83. QIN D T, ZHANG G H, KATO M. Research on mismatch point-contact hourglass worm[J]. Chinese Journal of Mechanical Engineering, 1995, 31(3): 79-83(in Chinese).
[15]	秦大同, 张光辉, 加藤正名. 锥面包络环面蜗杆与直廓环面蜗轮失配啮合传动的研究[J]. 重庆大学学报(自然科学版), 1995, 18(4): 15-20. QIN D T, ZHANG G H, KATO M. Study on mismatched engagement of hourglass worm gearing with the worm generated by a cone and the wheel generated by a straight profile hob[J]. Journal of Chongqing University (Natural Science Edition), 1995, 18(4): 15-20(in Chinese).
[16]	MENG Q X, ZHAO Y P, YANG Z Y, et al. Meshing theory and error sensitivity of mismatched conical surface enveloping conical worm pair[J]. Mechanism and Machine Theory, 2020, 145: 103681. doi: 10.1016/j.mechmachtheory.2019.103681
[17]	MENG Q X, ZHAO Y P, CUI J, et al. Meshing theory of mismatched ZC1 worm drive[J]. Mechanism and Machine Theory, 2020, 150: 103869. doi: 10.1016/j.mechmachtheory.2020.103869
[18]	CHI Y F, ZHAO Y P, ZHU X Y, et al. Mismatched gearing composed of hourglass worm and spur gear: Meshing theory, tooth contact simulation, comprehensive design[J]. Mechanism and Machine Theory, 2022, 174: 104883. doi: 10.1016/j.mechmachtheory.2022.104883
[19]	赵超飞, 魏冰阳. 直廓环面蜗杆-圆柱斜齿轮传动的几何建模与接触特性分析[J]. 机械传动, 2018, 42(11): 123-126. ZHAO C F, WEI B Y. Geometric modeling and contact characteristic analysis of hindley worm and cylindrical helical gear transmission[J]. Journal of Mechanical Transmission, 2018, 42(11): 123-126(in Chinese).
[20]	董学朱. 齿轮啮合理论基础[M]. 北京: 机械工业出版社,1989. DONG X Z. Foundation of gear engagement theory[M]. Beijing: China Machine Press, 1989(in Chinese).
[21]	REN W, LI H T, XU Z K, et al. A point-contact conjugate hourglass worm drive based on the meshing theory of conjugate tooth surfaces generated by two generating surfaces[J]. Mechanism and Machine Theory, 2022, 174: 104877. doi: 10.1016/j.mechmachtheory.2022.104877
[22]	董学朱, 李海清, 魏文军. 双自由度齿轮啮合理论及应用[M]. 北京: 机械工业出版社,2011. DONG X Z, LI H T, WEI W J. Theory and application of gear meshing with two degrees of freedom[M]. Beijing: China Machine Press, 2011(in Chinese).