基于非支配排序的并行加点方法研究及应用

刘睿; 白俊强; 邱亚松

doi:10.13700/j.bh.1001-5965.2022.0831

基于非支配排序的并行加点方法研究及应用

doi: 10.13700/j.bh.1001-5965.2022.0831

西北工业大学航空学院，西安 710072

详细信息

通讯作者:
E-mail：lr300150@163.com

中图分类号: V221
计量
- 文章访问数: 223
- HTML全文浏览量: 87
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-04
- 录用日期: 2022-12-30
- 网络出版日期: 2023-01-20
- 整期出版日期: 2023-06-30

Research and application of parallel infill sampling method based on non-dominated sorting

College of Aeronautics, Northwestern Polytechnical University，Xi’an 710072，China

More Information

Corresponding author: E-mail：lr300150@163.com

摘要

摘要:
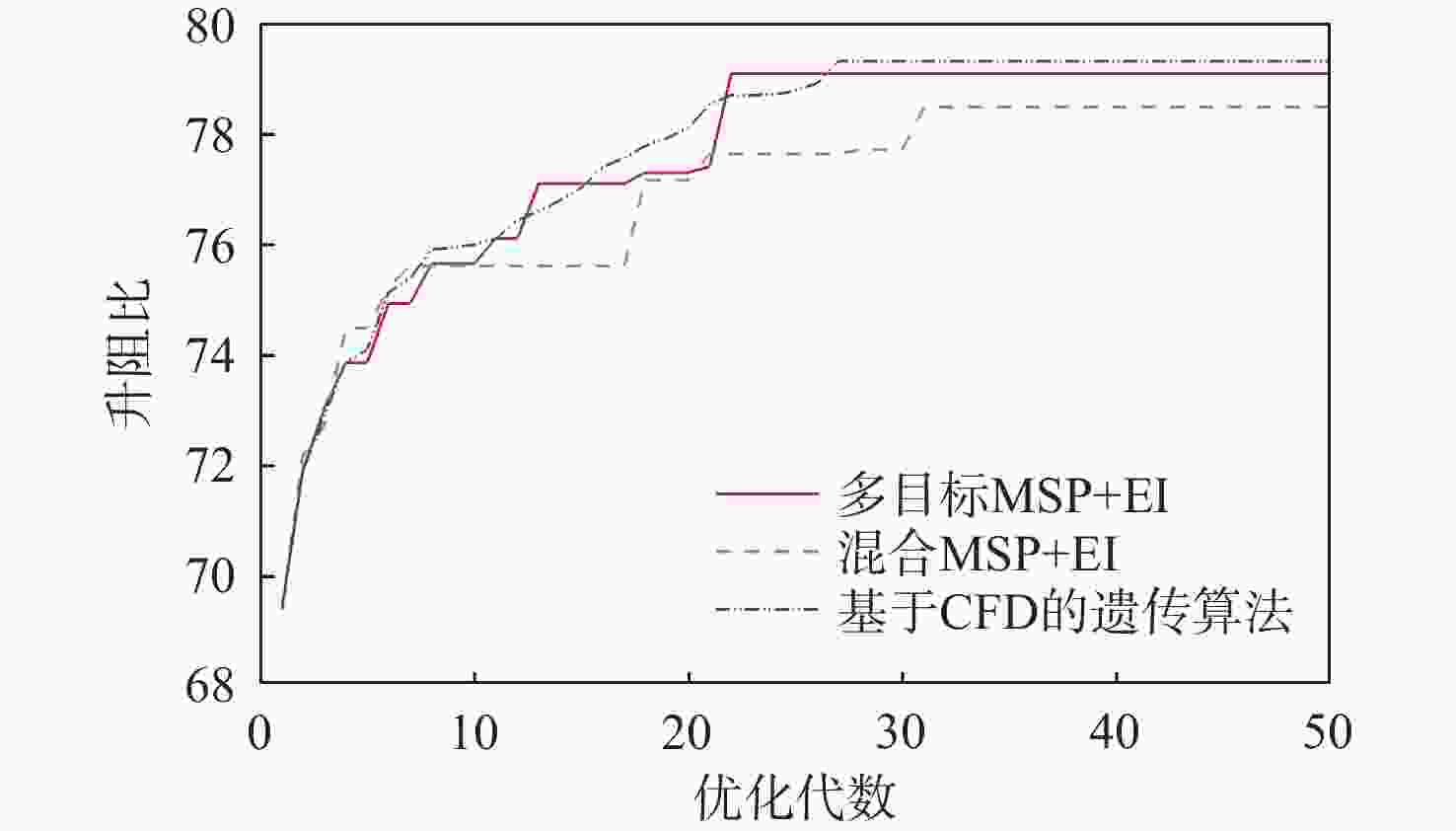
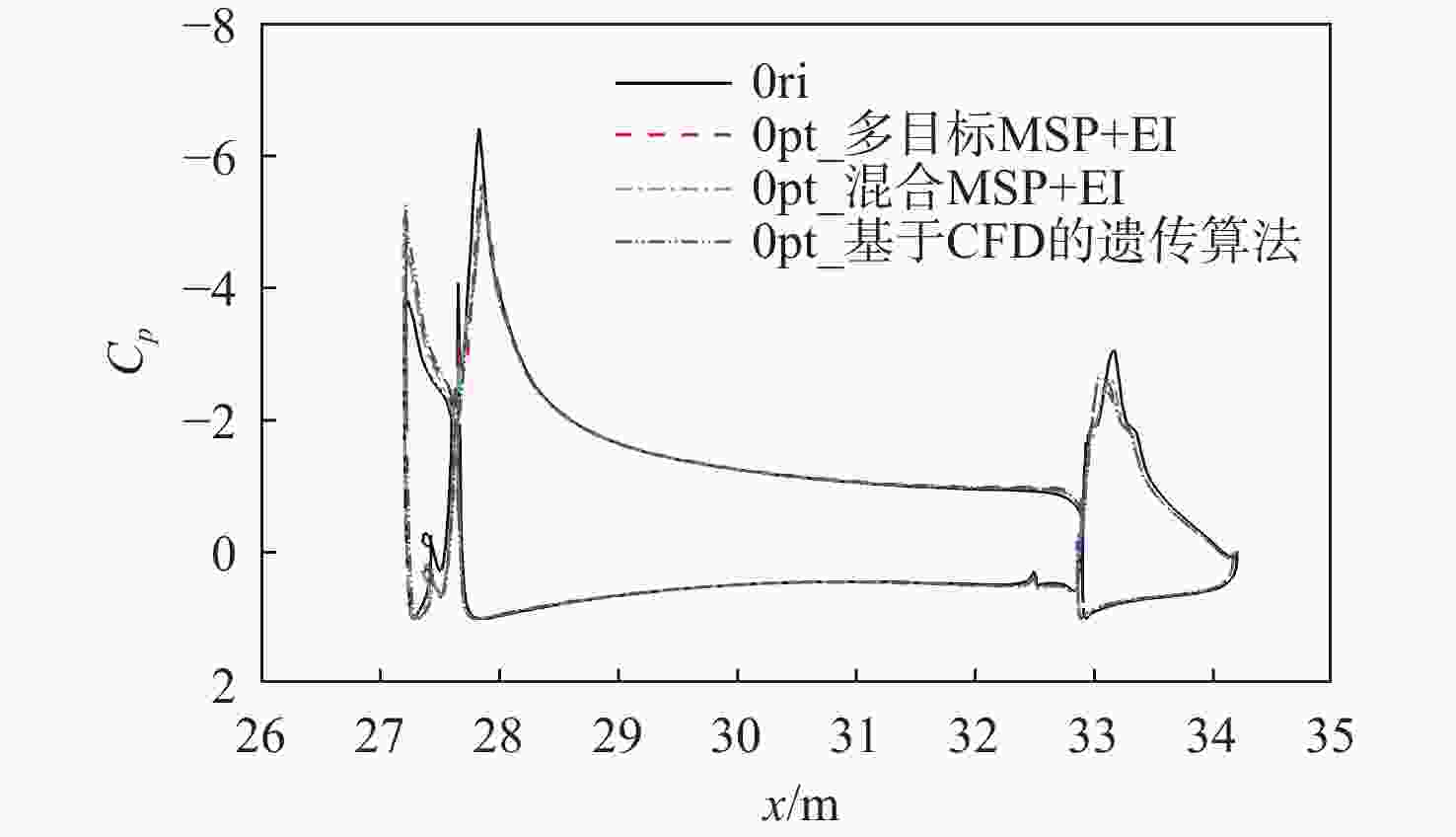
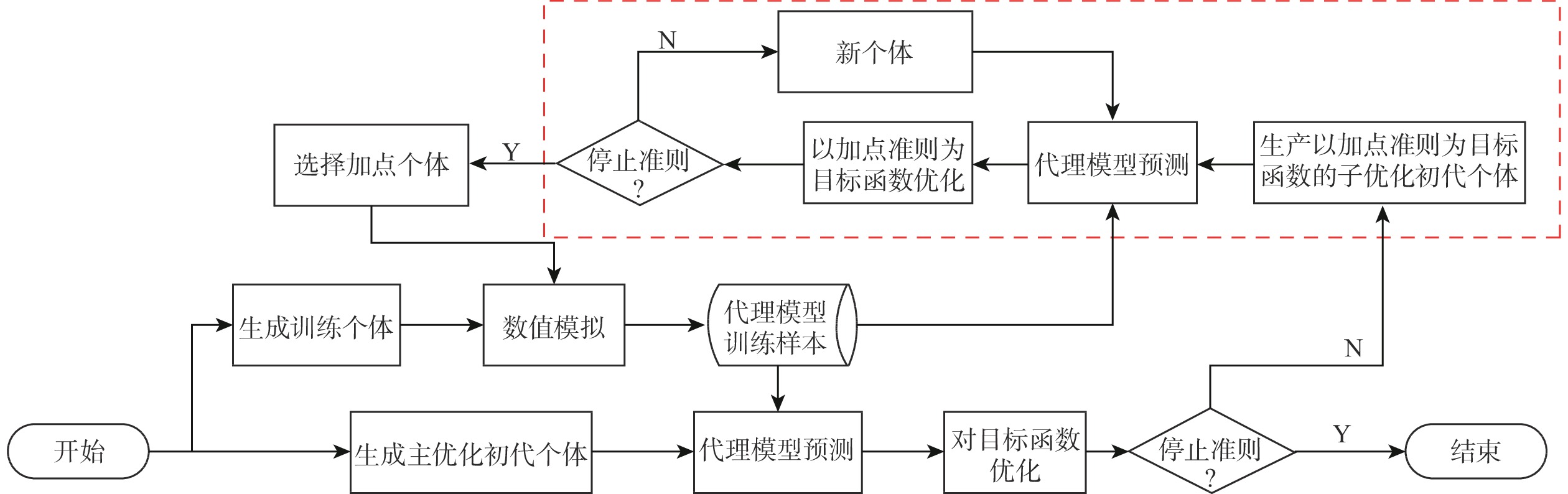
代理优化方法可以大幅提升高精度数值优化的效率，而加点方法对于优化结果和效率非常重要。并行加点方法一次可以添加多个训练样本，从而可以充分发挥计算资源的利用率，并且提高效率。在包含子优化的紧密式代理优化框架上将预测值、预测方差和期望改善(EI)函数值两两结合作为子优化目标，构建3种多目标并行加点方法，提出基于非支配排序的并行加点样本的策略。以SC(six-hump camel back)函数和2维GN(Griewank)函数、5维Rosenbrock函数及10维HD1(high-dimension 1)函数作为无约束优化算例，以7维G9函数作为约束优化算例，将构建的3种多目标并行加点方法与混合并行加点方法进行对比分析，结果表明：多目标并行加点方法效果较好。采用多目标并行加点方法、混合并行加点方法及基于计算流体力学(CFD)的遗传算法开展了二维多段翼型起飞状态的升阻比优化。优化结果表明：在升力系数不减小的约束下，多目标并行加点方法经过少量CFD评估，得到的优化结果使升阻比提升了14%，证明多目标并行加点方法在工程问题中的适用性。
- 非支配排序 /
- Kriging模型 /
- 优化设计 /
- 加点方法 /
- 多段翼型
Abstract:
The surrogate-based optimization method can greatly improve the efficiency of high-precision numerical optimization, while the infill sampling method is very important for the optimization result and efficiency. Several training samples can be infilled using the parallel infill sampling approach in a single step, fully using computer resources and increasing efficiency. In this article, based on the surrogate-based optimization framework including sub-optimization, three multi-objective parallel infill methods are constructed, using the prediction value, prediction variance and expected improvement(EI) function value as sub-optimization objectives. Besides, a strategy for selecting samples based on non-dominated sorting is proposed. Next, take the six-hump camel back(SC) function, the 2-dimensional griewank(GN) function, the 5-dimensional Rosenbrock function and the 10-dimensional high-dimension 1(HD1) function as unconstrained optimization examples, and the 7-dimensional G9 function as the constrained optimization example, the three multi-objective parallel infill sampling methods are compared with the hybrid parallel infill sampling methods. The outcomes demonstrate the superiority of the multi-objective parallel infill technique. Finally, the lift-drag ratio optimization of the two-dimensional multi-foil at take-off state was carried out by using the multi-objective infill sampling method, the hybrid parallel infill method and the genetic algorithm based on computational fluid dynamics(CFD). The optimization findings demonstrate the usefulness of the parallel infill sampling method in engineering issues by increasing the lift-to-drag ratio by 14% after a minimal amount of CFD evaluation under the constraint that the lift coefficient does not drop.
- non-dominant sorting /
- Kriging model /
- optimization design /
- infill sampling method /
- multi-foil

HTML全文

图 1 紧密式代理优化框架

Figure 1. Framework of inseparable surrogate-based optimization

下载: 全尺寸图片幻灯片

图 2 SC函数样本点分布

Figure 2. Sample distributions of SC function

下载: 全尺寸图片幻灯片

图 3 SC函数收敛历程

Figure 3. Convergence histories of SC function

下载: 全尺寸图片幻灯片

图 4 SC函数所有样本函数值

Figure 4. SC function values for all samples

下载: 全尺寸图片幻灯片

图 5 GN函数样本分布

Figure 5. Sample distributions of GN function

下载: 全尺寸图片幻灯片

图 6 GN函数收敛历程

Figure 6. Convergence histories of GN function

下载: 全尺寸图片幻灯片

图 7 GN函数所有样本函数值

Figure 7. GN function values for all samples

下载: 全尺寸图片幻灯片

图 8 RB5函数收敛历程

Figure 8. Convergence histories of RB5 function

下载: 全尺寸图片幻灯片

图 9 RB5函数所有样本函数值

Figure 9. RB5 function values for all samples

下载: 全尺寸图片幻灯片

图 10 HD1函数收敛历程

Figure 10. Convergence histories of HD1 function

下载: 全尺寸图片幻灯片

图 11 HD1函数所有样本函数值

Figure 11. HD1 function values for all samples

下载: 全尺寸图片幻灯片

图 12 G9函数收敛历程

Figure 12. Convergence histories of G9 function

下载: 全尺寸图片幻灯片

图 13 G9函数所有样本函数值

Figure 13. G9 function values for all samples

下载: 全尺寸图片幻灯片

图 14 多段翼型形状参数

Figure 14. Shape parameters of multi-foil

下载: 全尺寸图片幻灯片

图 15 二维多段翼型收敛历程

Figure 15. Convergence histories of multi-foil

下载: 全尺寸图片幻灯片

图 16 气动外形

Figure 16. Aerodynamic shapes

下载: 全尺寸图片幻灯片

图 17 压力分布

Figure 17. Pressure distributions

下载: 全尺寸图片幻灯片

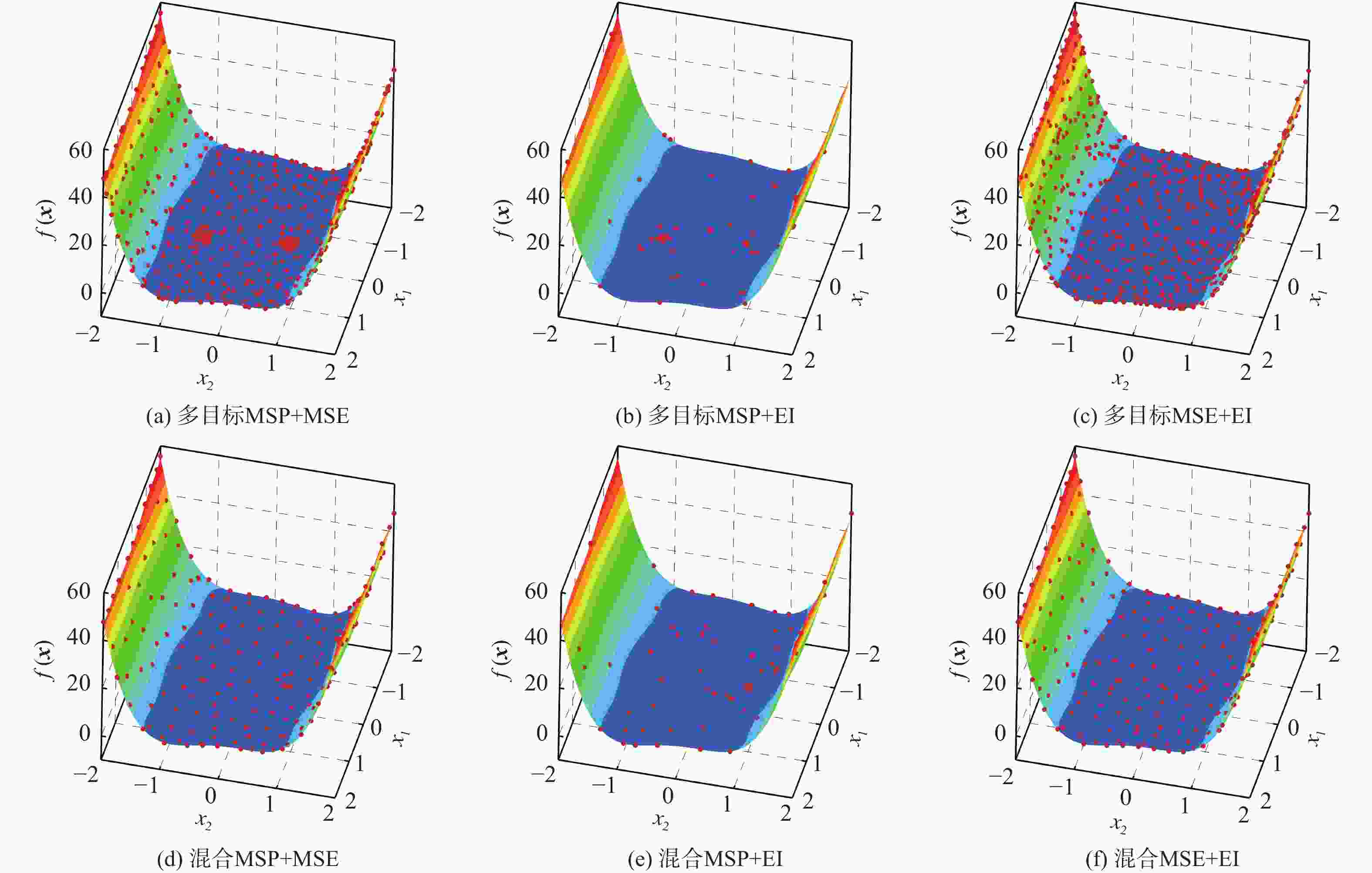
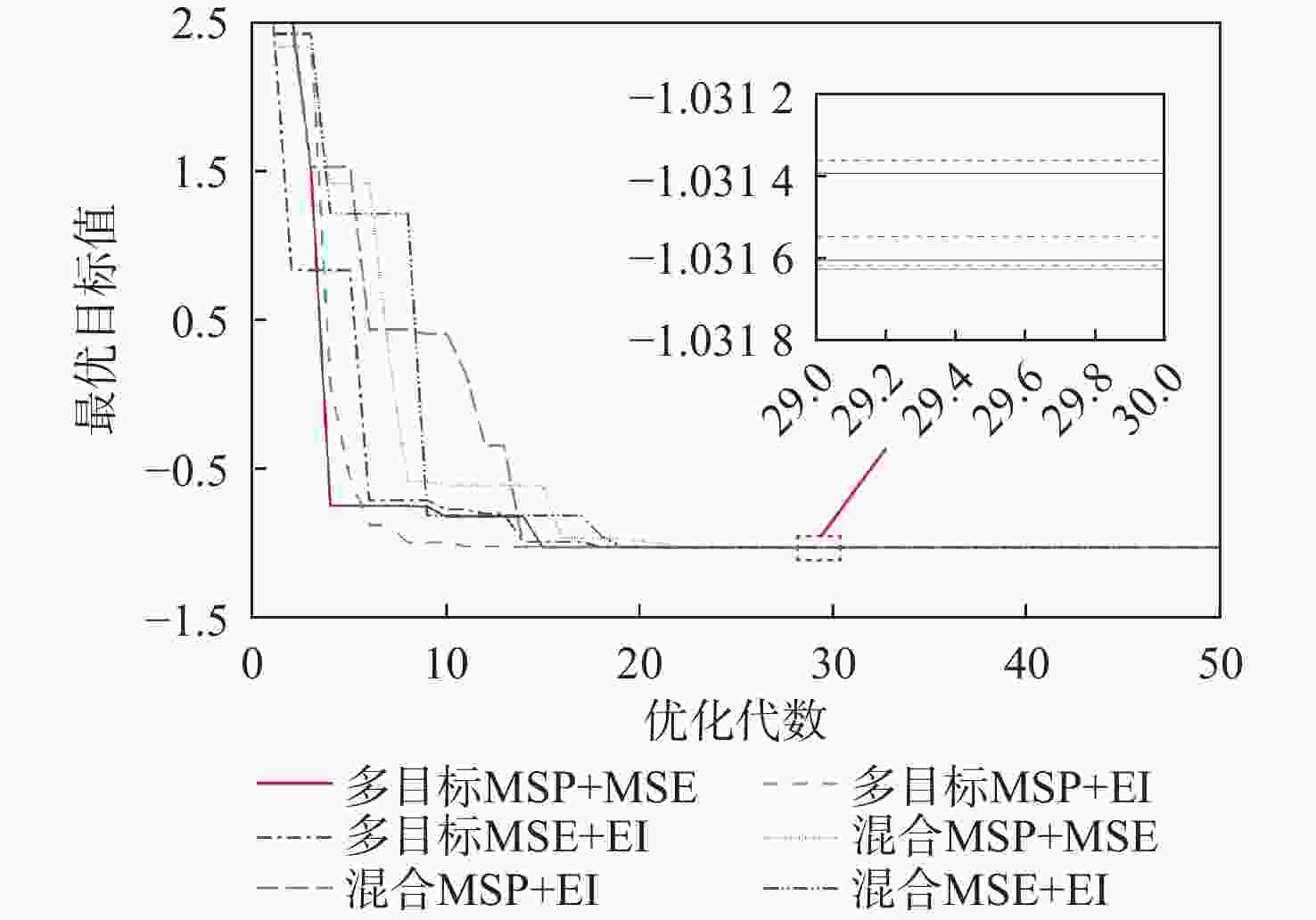
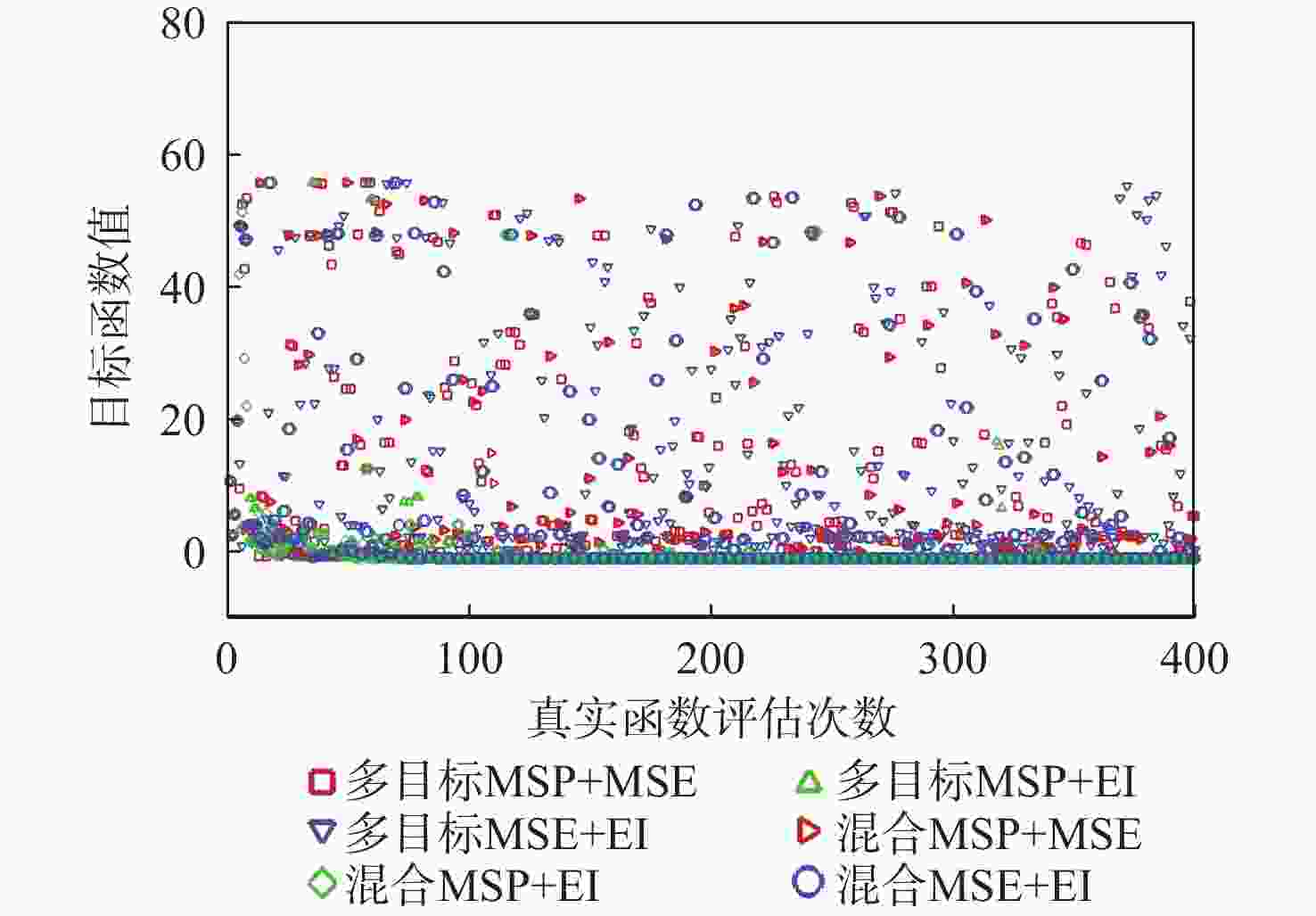
表 1 SC函数优化结果

Table 1. SC function optimization results

加点方法	最大最优解	最小最优解	平均最优解	方差
多目标MSP+MSE	−1.031585	−1.031608	−1.031586	7.919×10⁻¹¹
多目标MSP+EI	−1.031620	−1.031628	−1.031624	8.500×10⁻¹²
多目标MSE+EI	−1.031565	−1.031616	−1.031593	3.525×10⁻¹⁰
混合MSP+MSE	−1.031546	−1.031587	−1.031562	2.527×10⁻¹⁰
混合MSP+EI	−1.031606	−1.031617	−1.031612	1.219×10⁻¹¹
混合MSE+EI	−1.031502	−1.031547	−1.031525	3.977×10⁻¹⁰

下载: 导出CSV

表 2 GN函数优化结果对比

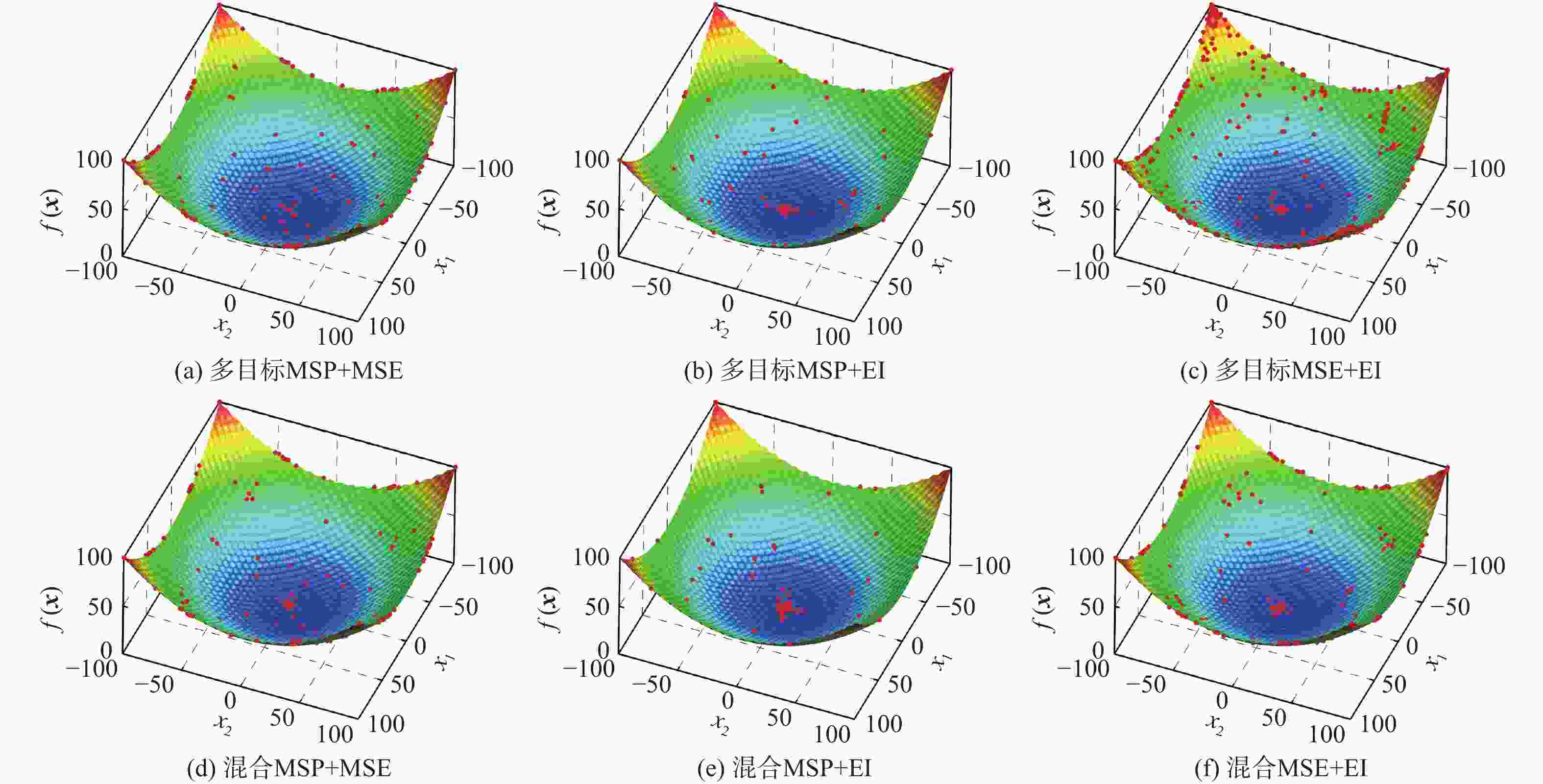
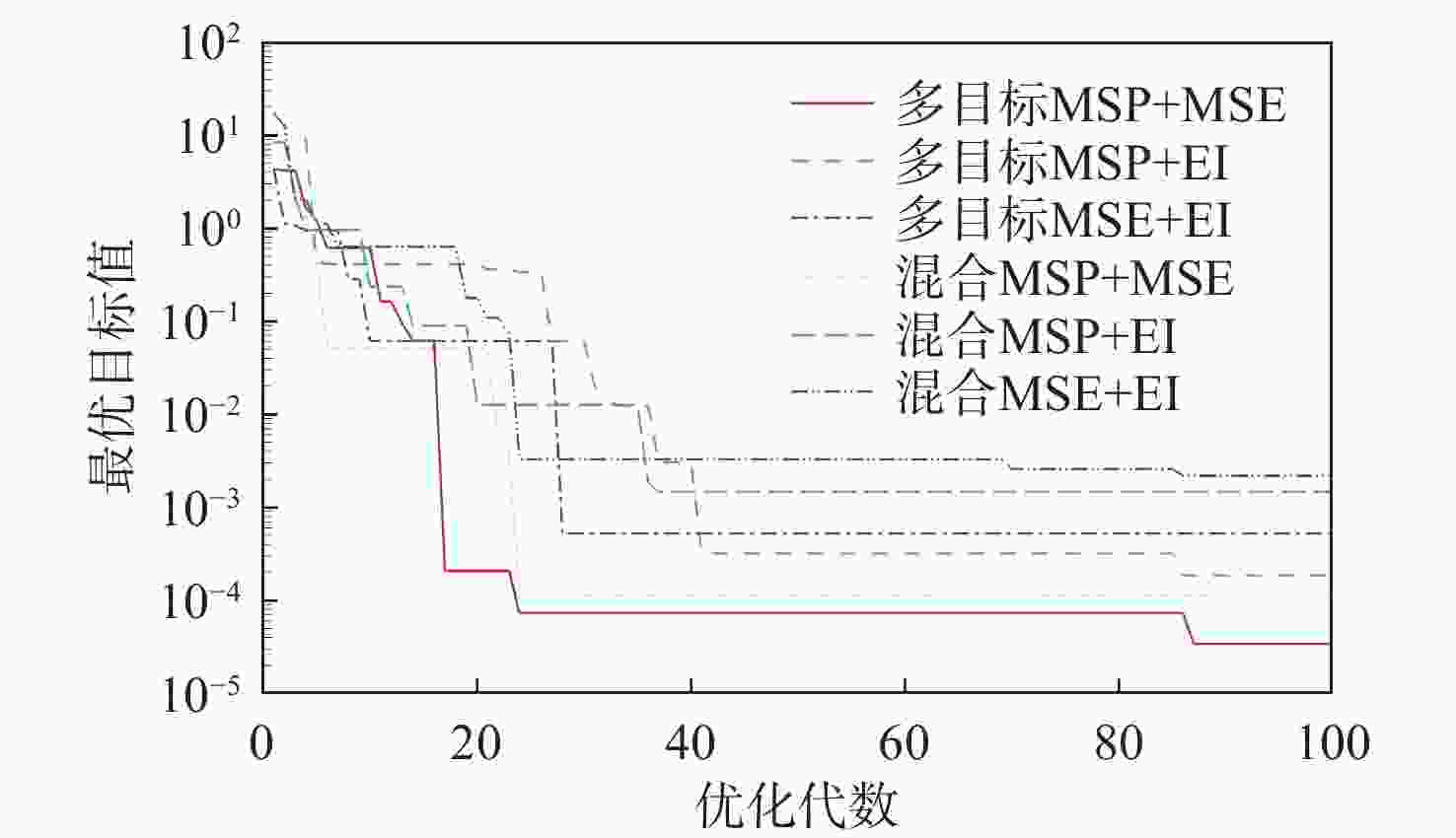
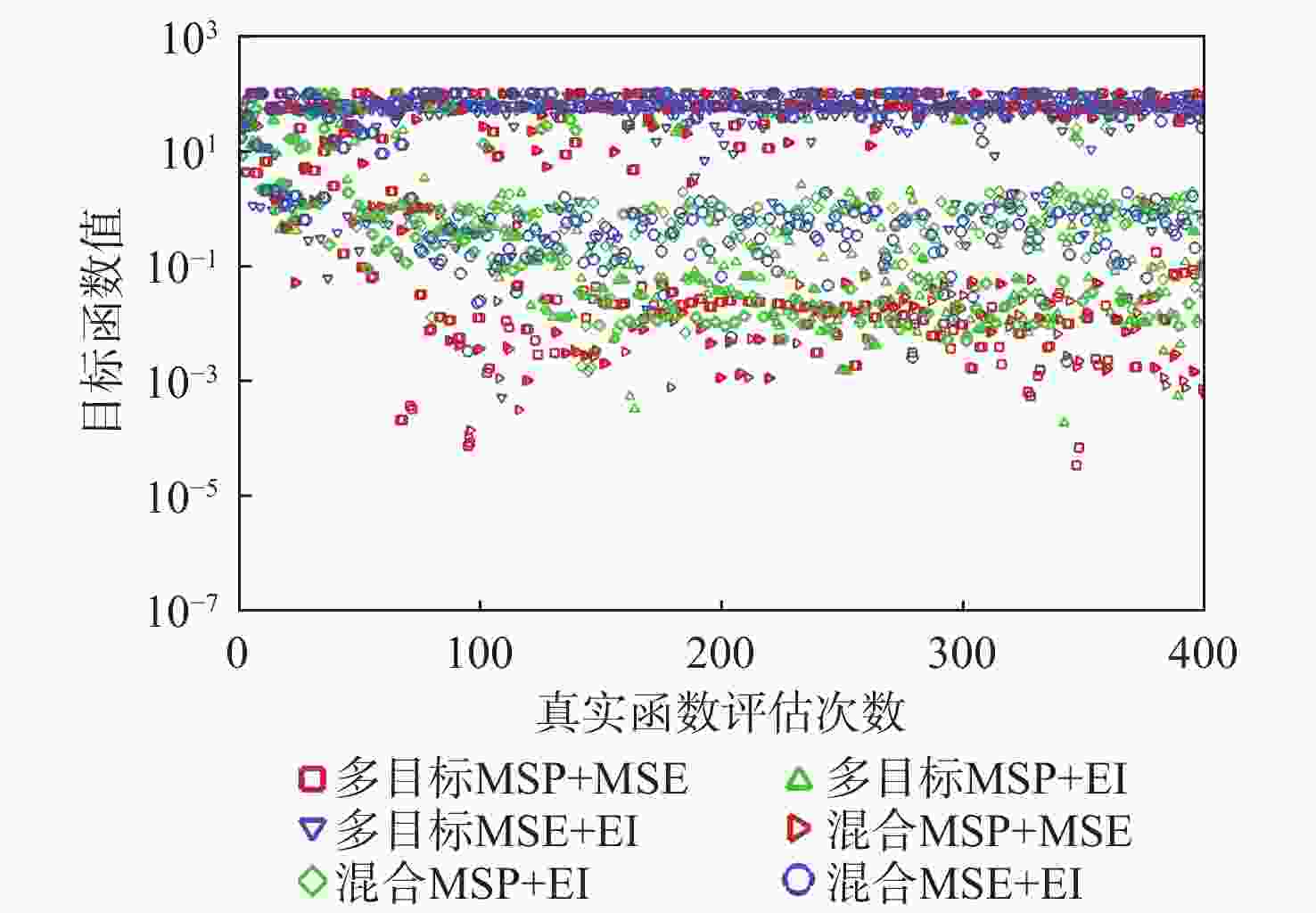
Table 2. Comparison of GN function optimization results

加点方法	最大最优解	最小最优解	平均最优解	方差
多目标MSP+MSE	0.1336×10⁻²	0.3400×10⁻⁴	0.5942×10⁻³	2.7742×10⁻⁷
多目标MSP+EI	0.3015×10⁻²	0.3191×10⁻³	0.2035×10⁻²	1.0961×10⁻⁶
多目标MSE+EI	0.1632×10⁻¹	0.5207×10⁻³	0.9236×10⁻²	4.4510×10⁻⁵
混合MSP+MSE	0.3238×10⁻²	0.1116×10⁻³	0.1305×10⁻²	1.4331×10⁻⁶
混合MSP+EI	0.7878×10⁻¹	0.1462×10⁻²	0.3933×10⁻¹	8.8700×10⁻⁴
混合MSE+EI	0.1889×10⁻¹	0.3288×10⁻²	0.1033×10⁻¹	3.1375×10⁻⁵

下载: 导出CSV

表 3 RB5函数优化结果

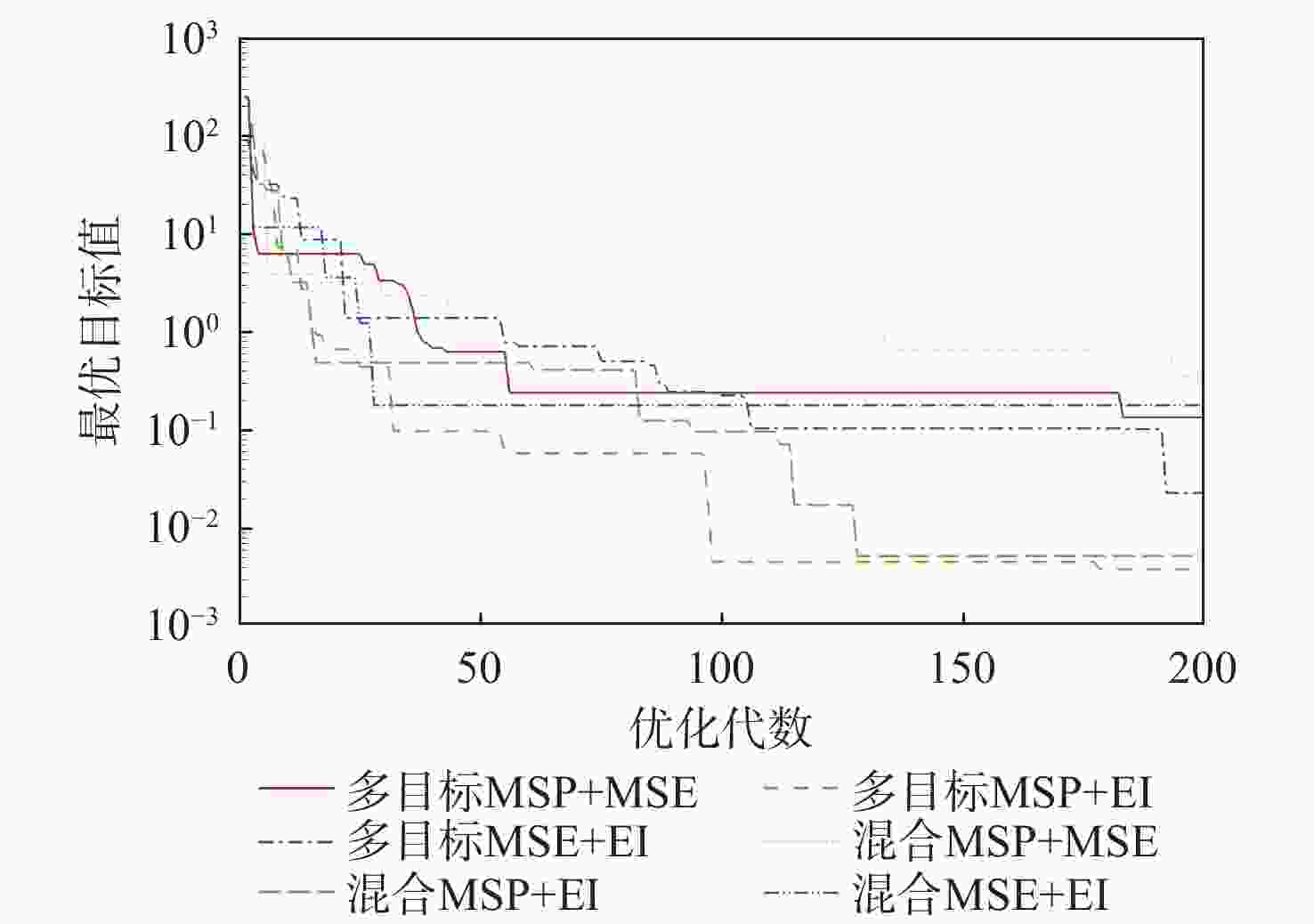
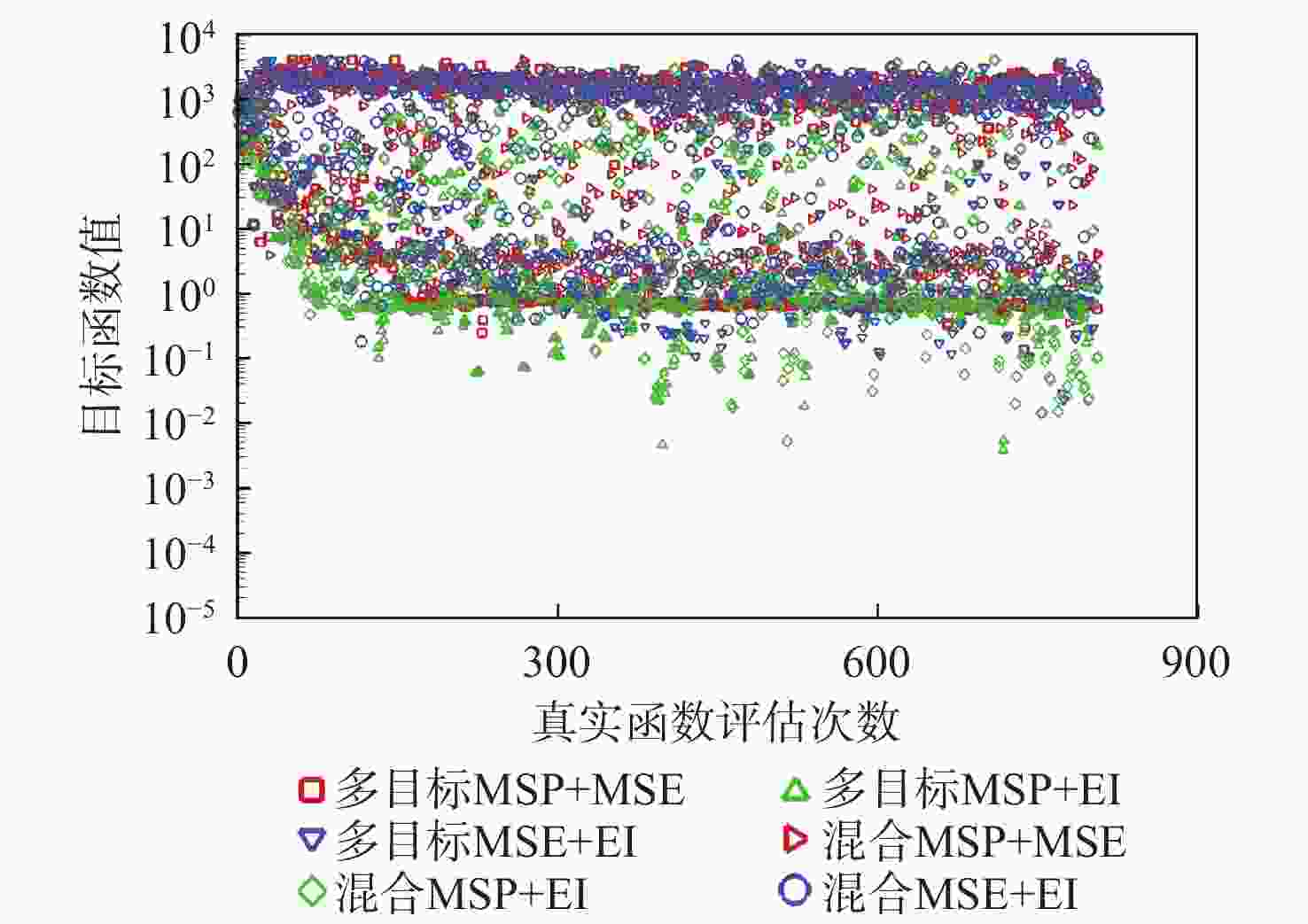
Table 3. RB5 function optimization results

加点方法	最大最优解	最小最优解	平均最优解	方差
多目标MSP+MSE	0.3688×10⁰	0.1346×10⁰	0.2380×10⁰	9.2365×10⁻³
多目标MSP+EI	0.1383×10⁻¹	0.3822×10⁻²	0.8861×10⁻²	1.9272×10⁻⁵
多目标MSE+EI	0.6197×10⁻¹	0.2293×10⁻¹	0.4350×10⁻¹	3.3689×10⁻⁴
混合MSP+MSE	0.5963×10⁰	0.3502×10⁰	0.4553×10⁰	8.1918×10⁻³
混合MSP+EI	0.3270×10⁻¹	0.5230×10⁻²	0.2063×10⁻¹	1.2910×10⁻⁴
混合MSE+EI	0.2858×10⁰	0.1793×10⁰	0.2326×10⁰	1.4606×10⁻³

下载: 导出CSV

表 4 HD1函数优化结果

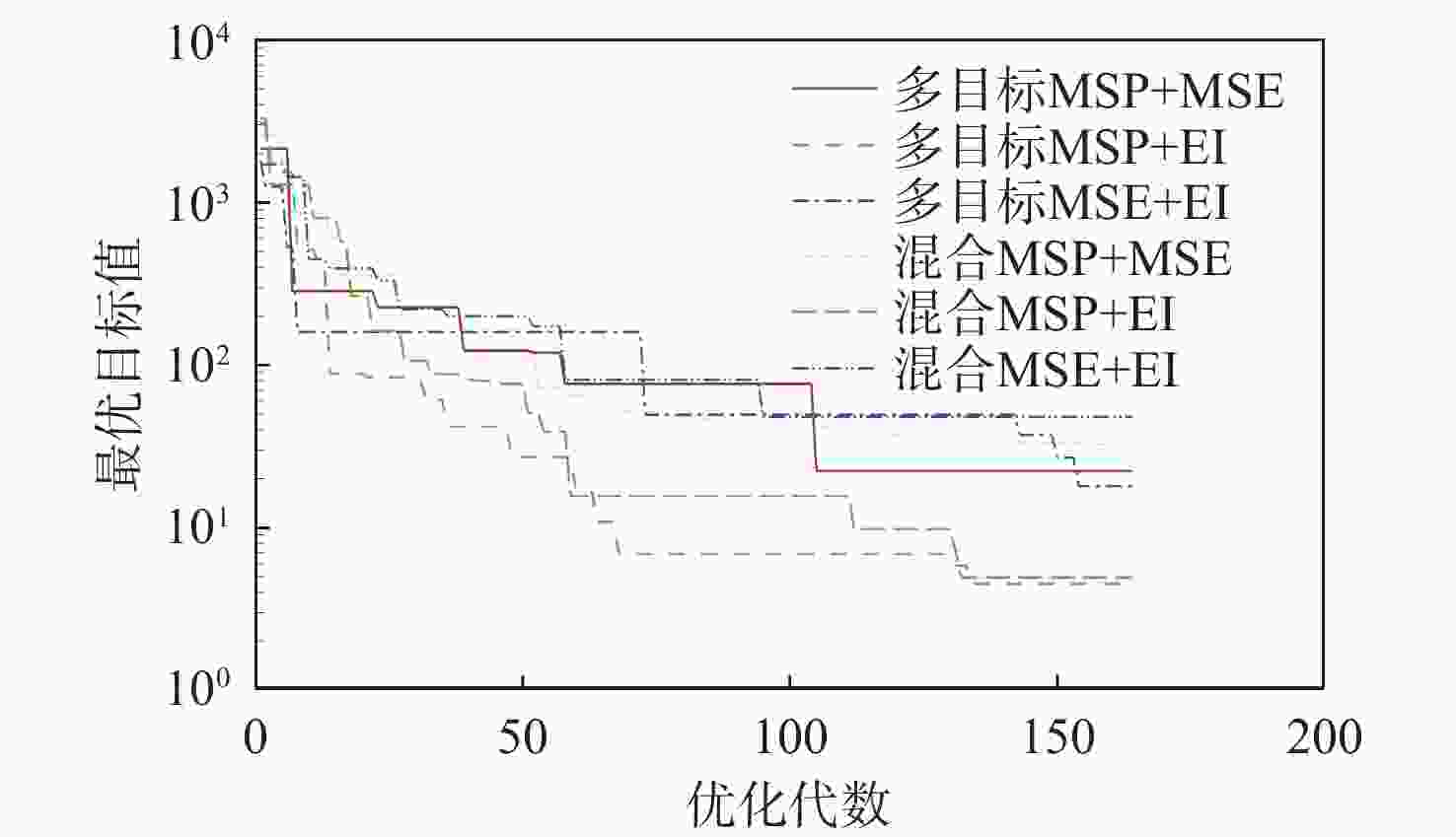
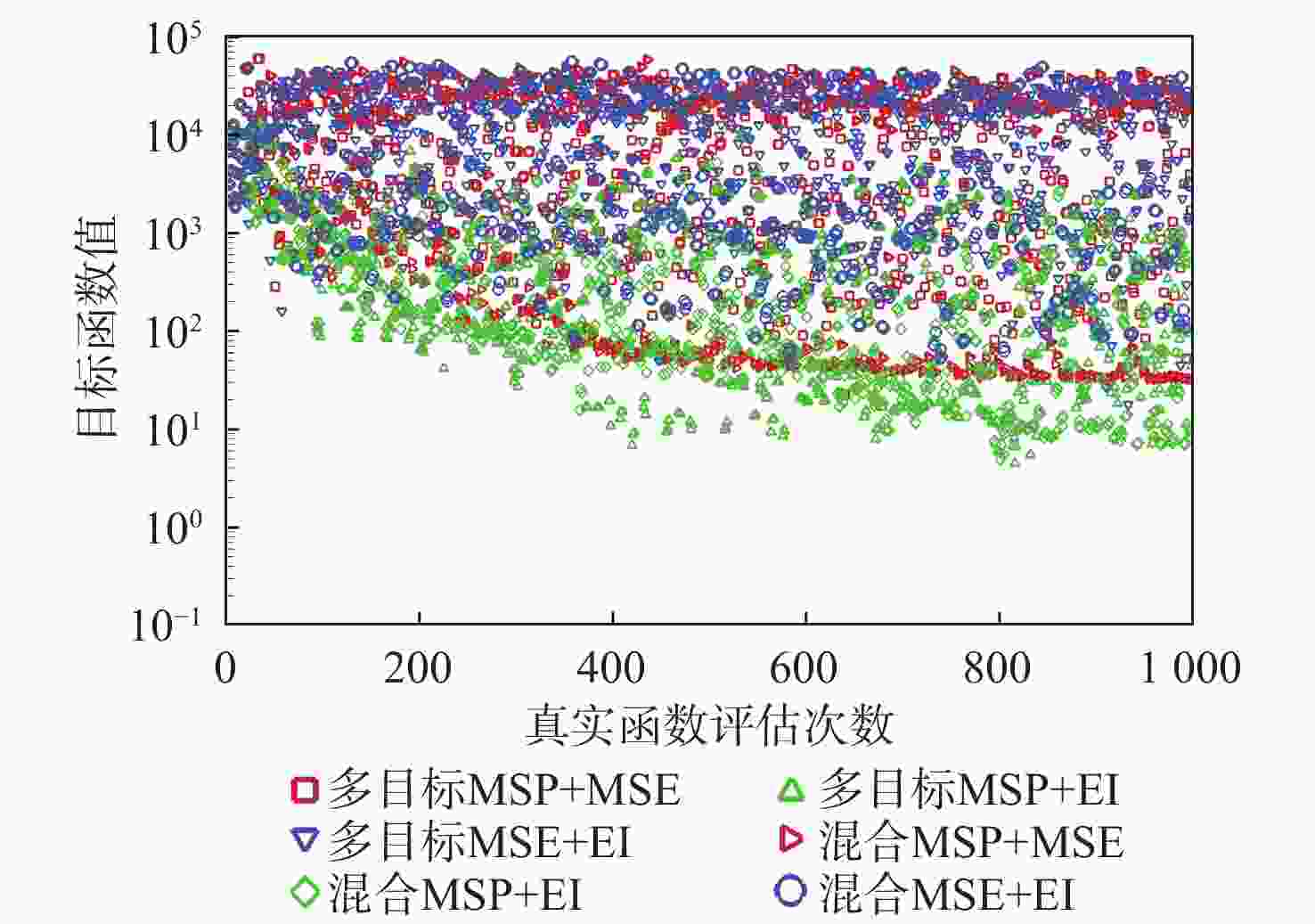
Table 4. HD1 function optimization results

加点方法	最大最优解	最小最优解	平均最优解	方差
多目标MSP+MSE	31.727	22.363	27.279	11.692
多目标MSP+EI	9.278	4.492	6.7265	3.308
多目标MSE+EI	26.879	17.885	22.354	12.197
混合MSP+MSE	42.145	32.427	37.042	12.072
混合MSP+EI	12.658	4.930	9.065	7.995
混合MSE+EI	58.527	48.084	53.356	14.805

下载: 导出CSV

表 5 G9函数优化结果对比

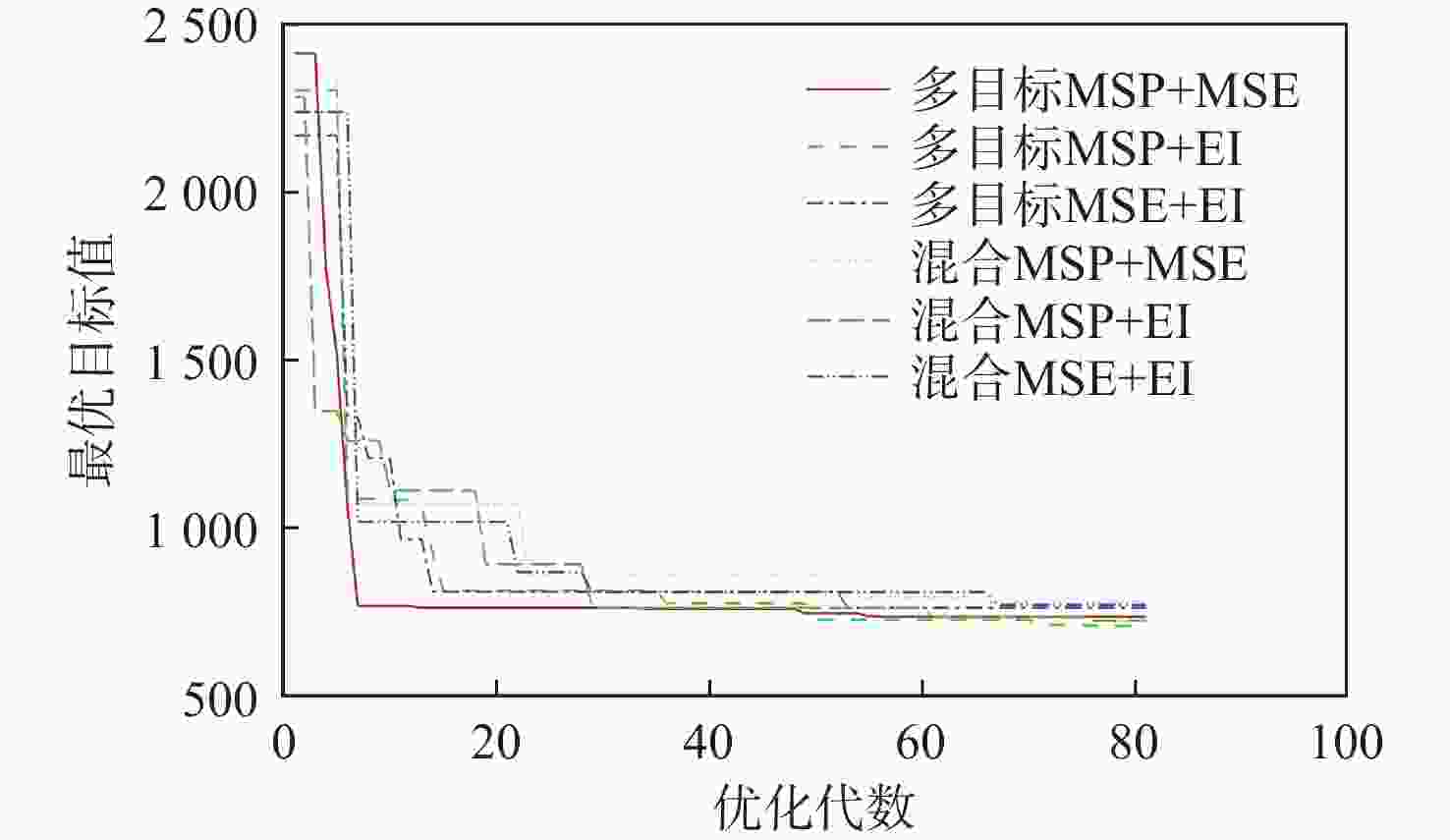
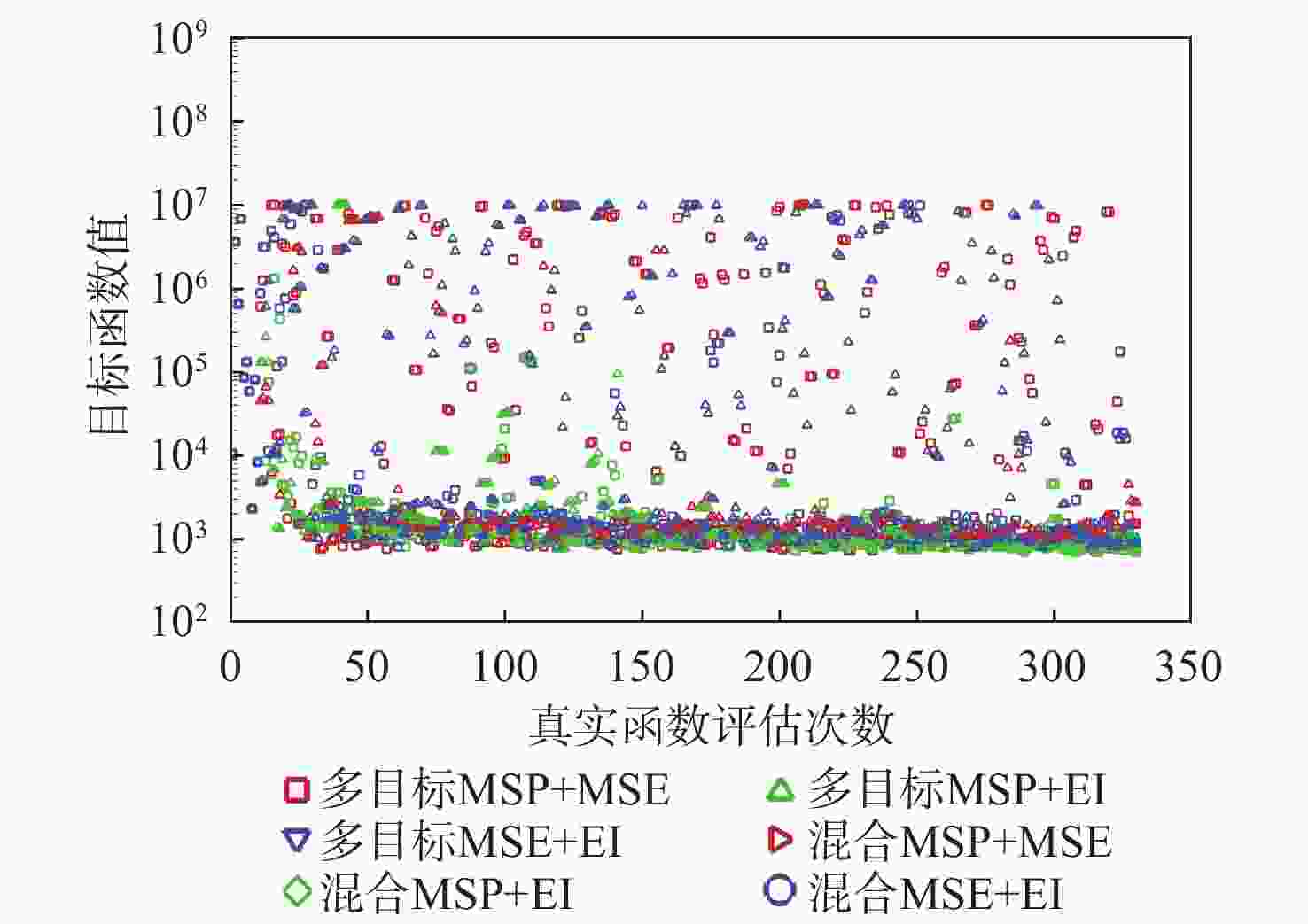
Table 5. Comparison of G9 function optimization results

加点方法	最大最优解	最小最优解	平均最优解	方差
多目标MSP+MSE	743.90	732.96	737.90	16.750
多目标MSP+EI	703.80	697.39	700.98	5.393
多目标MSE+EI	773.57	760.60	767.18	23.478
混合MSP+MSE	792.20	779.59	784.83	22.643
混合MSP+EI	734.87	722.61	728.21	15.863
混合MSE+EI	783.39	768.96	776.29	27.633

下载: 导出CSV

表 6 二维多段翼型优化设计空间

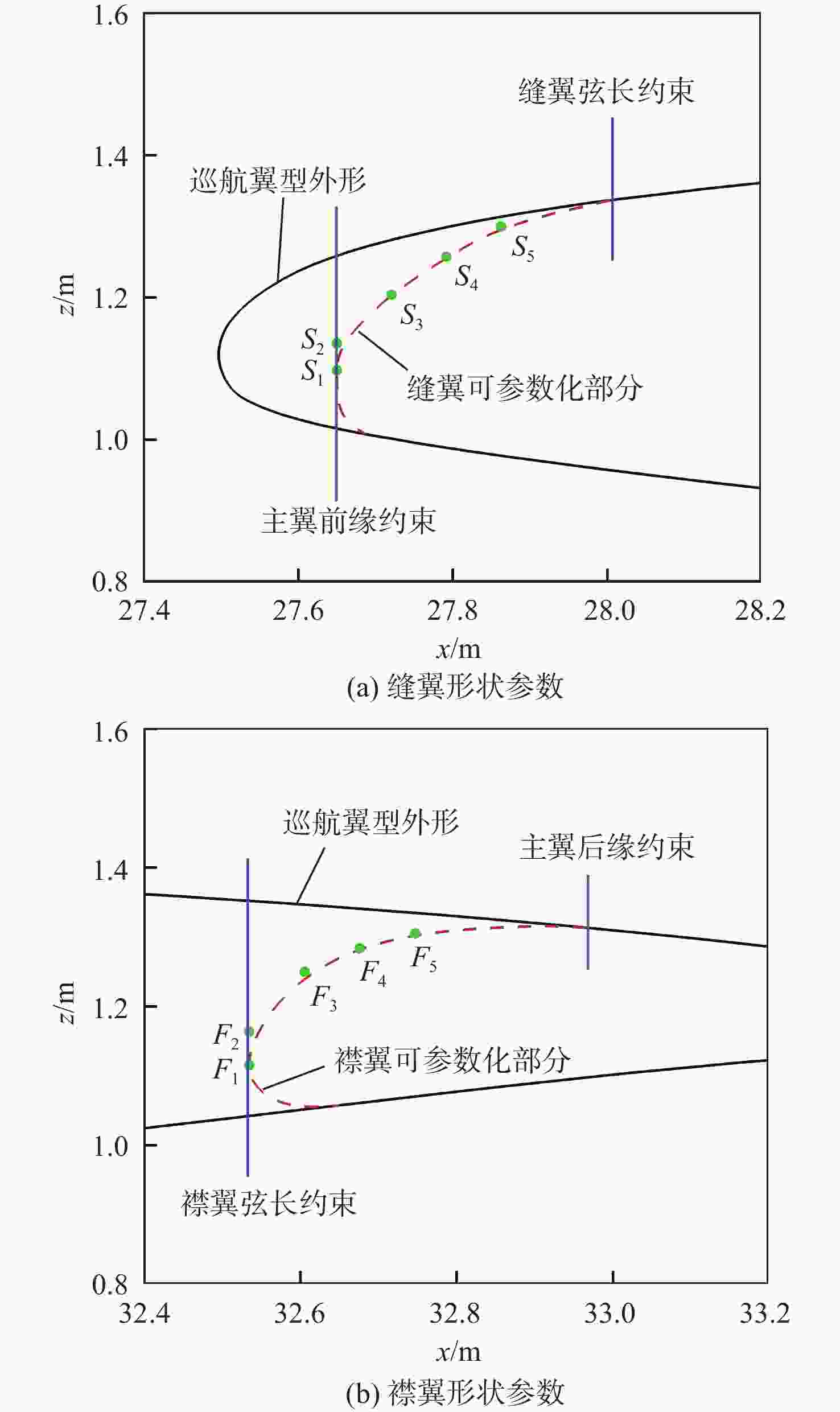
Table 6. Design space of multi-foil

参数		数值
参数		上边界	下边界
z方向/m	S₁	1.04584	1.09584
	S₂	1.09584	1.15584
	S₃	1.18922	1.22922
	S₄	1.25172	1.27172
	S₅	1.28972	1.30572
	F₁	1.09720	1.16073
	F₂	1.16073	1.21073
	F₃	1.22383	1.26383
	F₄	1.27170	1.30170
	F₅	1.29520	1.31020
搭接量	缝翼	−0.01	0.01
搭接量	襟翼	−0.01	0.01
缝道宽度	缝翼	0.005	0.02
缝道宽度	襟翼	0.005	0.02
偏转角度/(°)	缝翼	17	23
偏转角度/(°)	襟翼	20	26

下载: 导出CSV

参考文献(41)

[1]	POOLE D J, ALLEN C B, RENDALL T C S. High-fidelity aerodynamic shape optimization using efficient orthogonal modal design variables with a constrained global optimizer[J]. Computers & Fluids, 2017, 143: 1-15.
[2]	ZHANG T, BARAKOS G N. High-fidelity numerical analysis and optimisation of ducted propeller aerodynamics and acoustics[J]. Aerospace Science and Technology, 2021, 113: 106708. doi: 10.1016/j.ast.2021.106708
[3]	REIST T A, ZINGG D W. High-fidelity aerodynamic shape optimization of a lifting-fuselage concept for regional aircraft[J]. Journal of Aircraft, 2017, 54(3): 1085-1097. doi: 10.2514/1.C033798
[4]	GAGNON H, ZINGG D W. High-fidelity aerodynamic shape optimization of unconventional aircraft through axial deformation[C]// 52nd Aerospace Sciences Meeting. Reston: AIAA, 2014: 0908.
[5]	邱亚松. 基于数据降维技术的气动外形设计方法[D]. 西安: 西北工业大学, 2014. QIU Y S. Aerodynamic shape design methods based on data dimension approaches[D]. Xi’an: Northwestern Polytechnical University, 2014 (in Chinese).
[6]	MACK Y, GOEL T, SHYY W, et al. Surrogate model-based optimization framework: A case study in aerospace design[M]. Evolutionary Computation in Dynamic and Uncertain Environments. Berlin: Springer, 2007: 323-342.
[7]	KHURI A I, MUKHOPADHYAY S. Response surface methodology[J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2010, 2(2): 128-149. doi: 10.1002/wics.73
[8]	HU Z, MAHADEVAN S. A single-loop kriging surrogate modeling for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2016, 138(6): 061406. doi: 10.1115/1.4033428
[9]	REGIS R G, SHOEMAKER C A. Combining radial basis function surrogates and dynamic coordinate search in high-dimensional expensive black-box optimization[J]. Engineering Optimization, 2013, 45(5): 529-555. doi: 10.1080/0305215X.2012.687731
[10]	PFROMMER J, ZIMMERLING C, LIU J Z, et al. Optimisation of manufacturing process parameters using deep neural networks as surrogate models[J]. Procedia CIRP, 2018, 72: 426-431. doi: 10.1016/j.procir.2018.03.046
[11]	XIANG H Y, LI Y L, LIAO H L, et al. An adaptive surrogate model based on support vector regression and its application to the optimization of railway wind barriers[J]. Structural and Multidisciplinary Optimization, 2017, 55(2): 701-713. doi: 10.1007/s00158-016-1528-9
[12]	韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225(in Chinese).
[13]	KOCH P N, SIMPSON T W, ALLEN J K, et al. Statistical approximations for multidisciplinary design optimization: The problem of size[J]. Journal of Aircraft, 1999, 36(1): 275-286. doi: 10.2514/2.2435
[14]	刘俊. 基于代理模型的高效气动优化设计方法及应用[D]. 西安: 西北工业大学, 2015. LIU J. Efficient surrogate-based optimization method and its application in aerodynamic design[D]. Xi’an: Northwestern Polytechnical University, 2015 (in Chinese).
[15]	HAN Z H, ZHANG K S. Surrogate-based optimization[M]. Real-World Applications of Genetic Algorithms. Houston: InTech, 2012.
[16]	LIU J, HAN Z H, SONG W. Comparison of infill sampling criteria in kriging-based aerodynamic optimization[C]//28th Congress of the International Council of the Aeronautical Sciences. Brisbane: The International Council of the Aeronautical Sciences, 2012: 23-28.
[17]	JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. doi: 10.1023/A:1008306431147
[18]	SASENA M J, PAPALAMBROS P, GOOVAERTS P. Exploration of metamodeling sampling criteria for constrained global optimization[J]. Engineering Optimization, 2002, 34(3): 263-278. doi: 10.1080/03052150211751
[19]	JONES D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21(4): 345-383. doi: 10.1023/A:1012771025575
[20]	CHEVALIER C, GINSBOURGER D. Fast Computation of the multi-points expected improvement with applications in batch selection[C]//International Conference on Learning and Intelligent Optimization. Berlin: Springer, 2013: 59-69.
[21]	SÓBESTER A, LEARY S J, KEANE A J. A parallel updating scheme for approximating and optimizing high fidelity computer simulations[J]. Structural and Multidisciplinary Optimization, 2004, 27(5): 371-383.
[22]	GINSBOURGER D, LE RICHE R, CARRARO L. Kriging is well-suited to parallelize optimization[M]. Computational Intelligence in Expensive Optimization Problems. Berlin: Springer, 2010: 131-162.
[23]	LI Z, RUAN S L, GU J F, et al. Investigation on parallel algorithms in efficient global optimization based on multiple points infill criterion and domain decomposition[J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 747-773. doi: 10.1007/s00158-016-1441-2
[24]	FENG Z W, ZHANG Q B, ZHANG Q F, et al. A multiobjective optimization based framework to balance the global exploration and local exploitation in expensive optimization[J]. Journal of Global Optimization, 2015, 61(4): 677-694. doi: 10.1007/s10898-014-0210-2
[25]	SEKISHIRO M, VENTER G, BALABANOV V. Combined Kriging and gradient-based optimization method[C]//11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2006: 7091.
[26]	CHAUDHURI A, HAFTKA R T, IFJU P, et al. Experimental flapping wing optimization and uncertainty quantification using limited samples[J]. Structural and Multidisciplinary Optimization, 2015, 51(4): 957-970. doi: 10.1007/s00158-014-1184-x
[27]	BISCHL B, WESSING S, BAUER N, et al. MOI-MBO: Multiobjective infill for parallel model-based optimization[C]//International Conference on Learning and Intelligent Optimization. Berlin: Springer, 2014: 173-186.
[28]	LIU J, SONG W P, HAN Z H, et al. Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models[J]. Structural and Multidisciplinary Optimization, 2017, 55(3): 925-943. doi: 10.1007/s00158-016-1546-7
[29]	LOCATELLI M. Bayesian algorithms for one-dimensional global optimization[J]. Journal of Global Optimization, 1997, 10(1): 57-76. doi: 10.1023/A:1008294716304
[30]	LI C N, PAN Q F. Adaptive optimization methodology based on Kriging modeling and a trust region method[J]. Chinese Journal of Aeronautics, 2019, 32(2): 281-295. doi: 10.1016/j.cja.2018.11.012
[31]	MA J, LI H M. Research on rosenbrock function optimization problem based on improved differential evolution algorithm[J]. Journal of Computer and Communications, 2019, 7(11): 107-120. doi: 10.4236/jcc.2019.711008
[32]	KRIGE D. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the Southern African Institute of Mining and Metallurgy, 1951, 52(6): 119-139.
[33]	SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science, 1989, 4(4): 409-423.
[34]	STORN R, PRICE K. DE-a simple and efficient adaptive scheme for global optimization over continuous space[J]. Technical Report, 1995, 25(6): 95-102.
[35]	CHAIYARATANA N, PIROONRATANA T, SANGKAWELERT N. Effects of diversity control in single-objective and multi-objective genetic algorithms[J]. Journal of Heuristics, 2007, 13(1): 1-34. doi: 10.1007/s10732-006-9003-1
[36]	DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017
[37]	JOHNSON M E, MOORE L M, YLVISAKER D. Minimax and maximin distance designs[J]. Journal of Statistical Planning and Inference, 1990, 26(2): 131-148. doi: 10.1016/0378-3758(90)90122-B
[38]	ZHANG D Y, WANG Z D, LING H J, et al. Kriging-based shape optimization framework for blended-wing-body underwater glider with NURBS-based parametrization[J]. Ocean Engineering, 2021, 219: 108212. doi: 10.1016/j.oceaneng.2020.108212
[39]	BOER A D, VAN DER SCHOOT M S, BIJL H. Mesh deformation based on radial basis function interpolation[J]. Computers & Structures, 2007, 85(11-14): 784-795.
[40]	秦绪国, 刘沛清, 屈秋林, 等. 缝道参数对多段翼型气动性能的影响[J]. 北京航空航天大学学报, 2011, 37(2): 193-196. doi: 10.13700/j.bh.1001-5965.2011.02.012 QIN X G, LIU P Q, QU Q L, et al. Influence of gap parameters on aerodynamics of multi-element airfoil[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(2): 193-196(in Chinese). doi: 10.13700/j.bh.1001-5965.2011.02.012
[41]	SMITH A M O. High-lift aerodynamics[J]. Journal of Aircraft, 1975, 12(6): 501-530. doi: 10.2514/3.59830