Multi-objective optimization of airport runway construction schemes based on improved genetic algorithm
-
摘要:
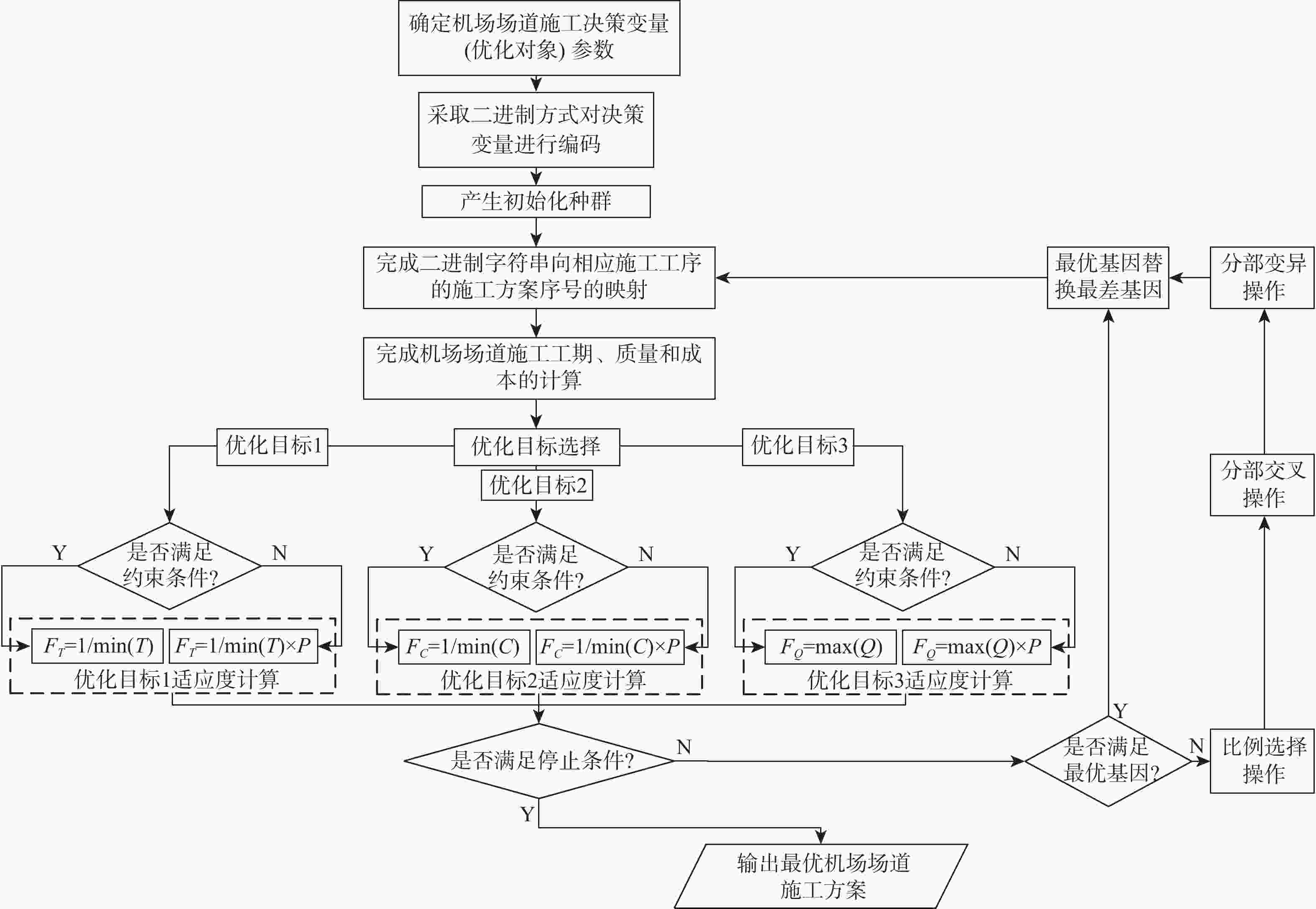
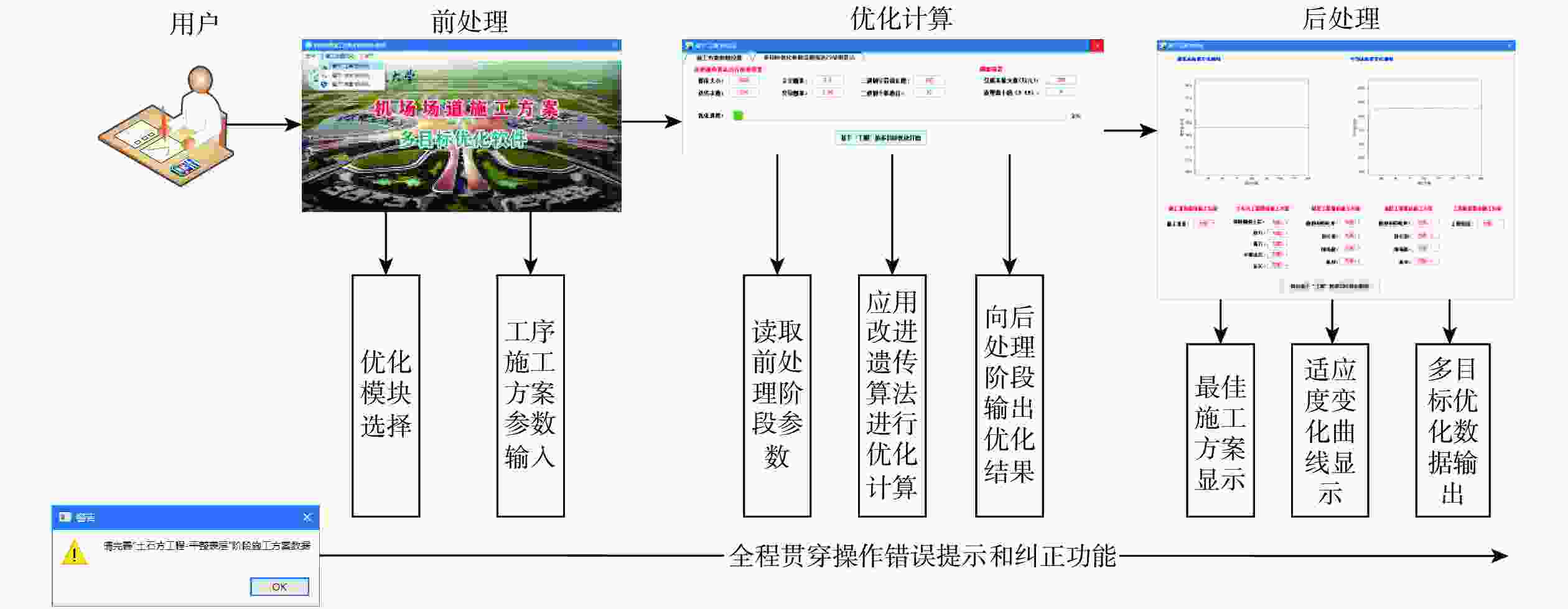
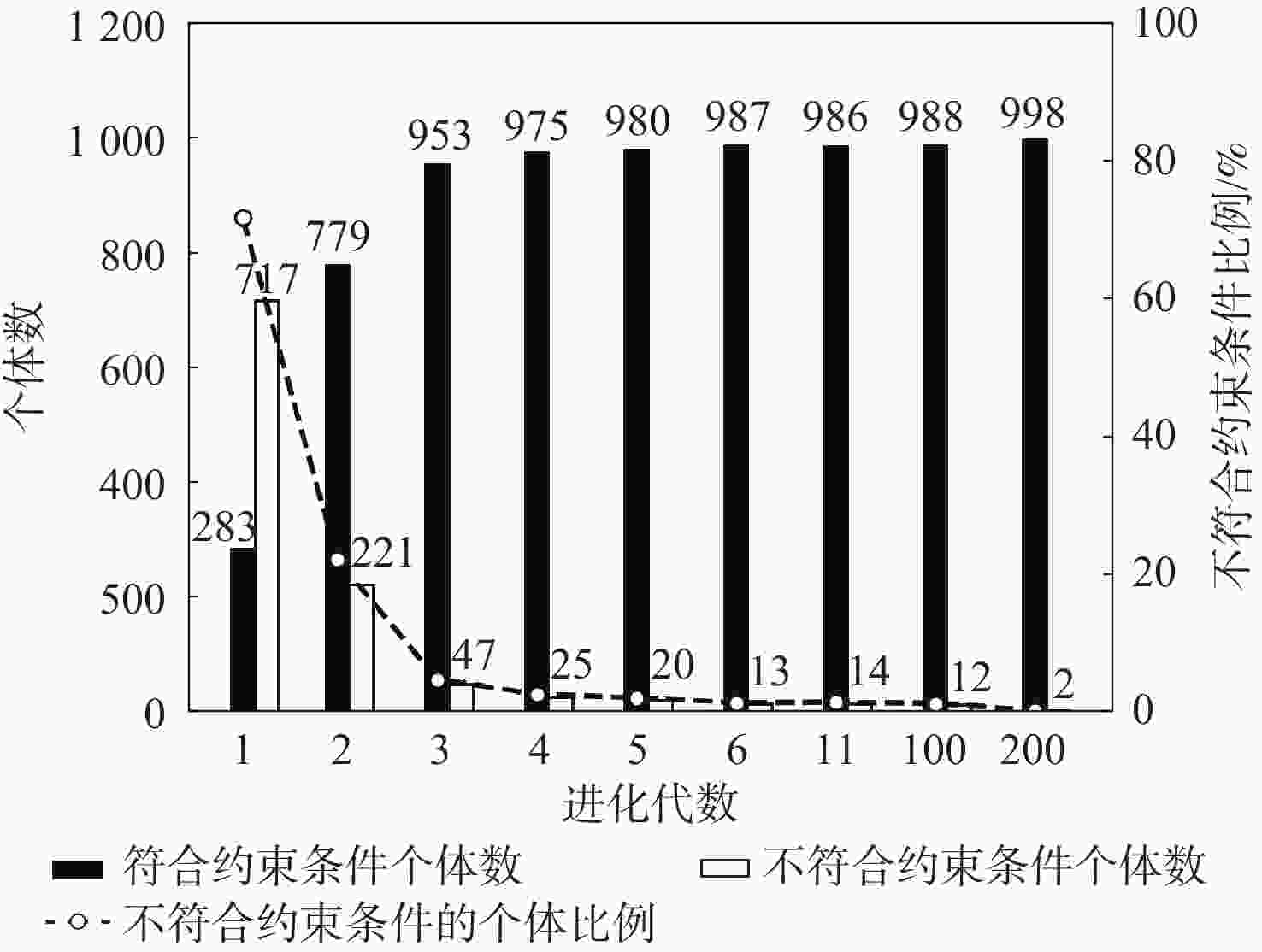
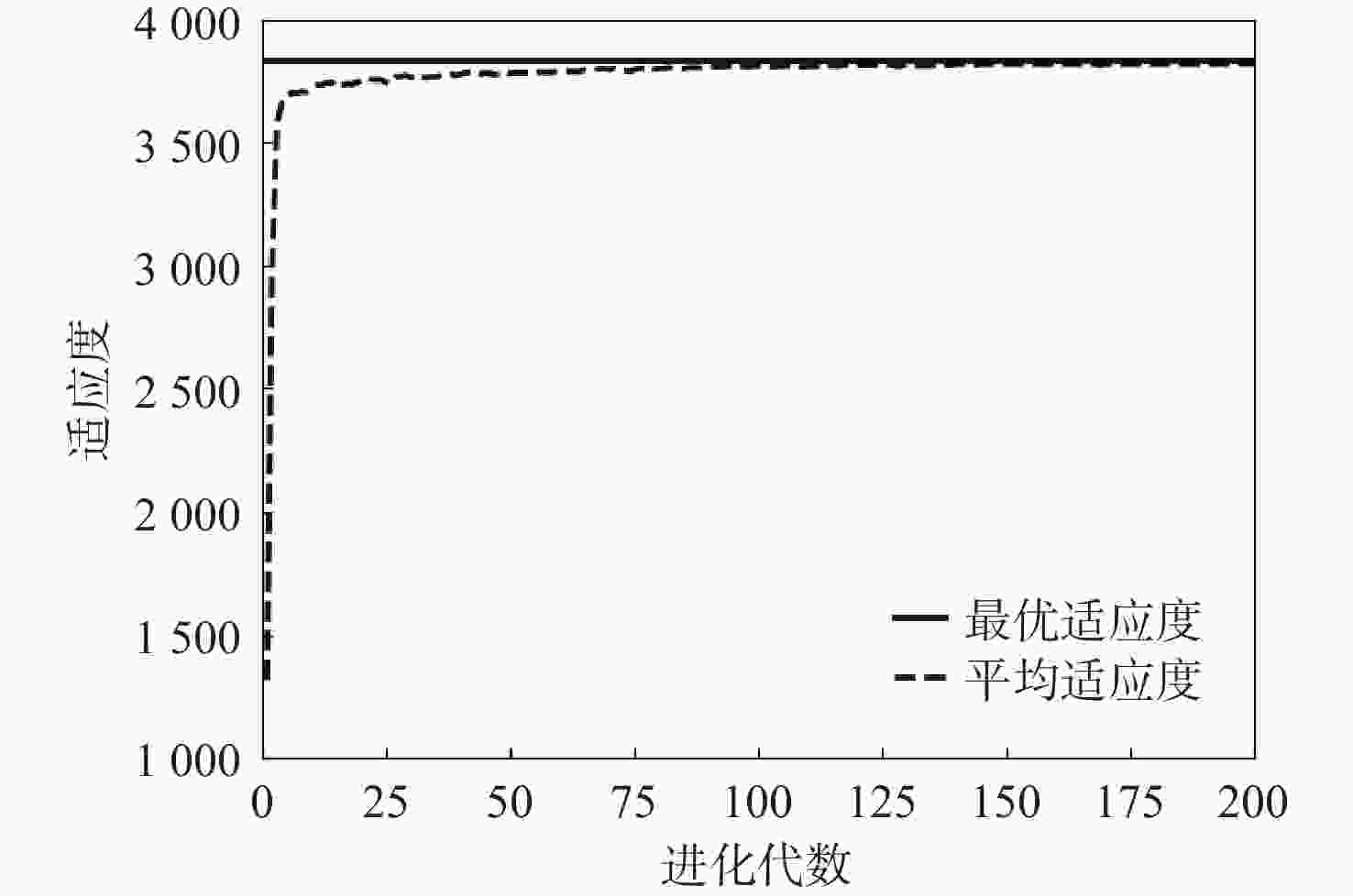
为解决机场场道项目管理过程中,针对不同施工目标、施工工序中施工方案的选取问题,通过对机场场道施工工序多种施工方案的分析,从工期、质量和成本3个维度分别建立数学模型,在此基础上,采用改进遗传算法,以机场场道施工工序中施工方案为优化对象,以工期、质量和成本为优化目标,构建机场场道施工方案的多目标优化模型。采用Python语言,搭建面向对象的机场场道施工方案多目标优化的通用性框架,并基于PyQt5,实现参数输入、施工方案优化、优化结果输出功能的软件界面开发。以满足一定质量和成本为前提、工期最短为优化目标,对软件的优化性能进行了验证,通过对优化结果的分析表明:应用改进遗传算法,可有效进行机场场道施工方案的多目标优化,优化结果正确,满足优化目标的需求,可为机场场道施工项目决策提供参考。
Abstract:In order to select the optimal construction scheme during the construction process for different construction objectives in the airport runway project management, various construction schemes for the airport runway construction process were analyzed, and the mathematical models were established in terms of the construction period, quality, and cost. On this basis, the improved genetic algorithm was used, and the construction scheme for the airport runway construction process was taken as the optimization object. The construction period, quality, and cost were set as the optimization objectives, and a multi-objective optimization model of the airport runway construction scheme was constructed. Then, the general framework of object-oriented multi-objective optimization of airport runway construction schemes was built by using Python language, and the software interface development with the functions of parameter input, construction scheme optimization, and optimization result output was realized based on PyQt5. Finally, on the premise of meeting certain quality and cost, with the shortest construction period as the optimization objective, the optimization performance of the software was verified. The analysis of the optimization results shows that the application of the improved genetic algorithm can effectively achieve the multi-objective optimization of airport runway construction schemes. The optimization results are correct and meet the needs of optimization objectives, which can provide a reference for decision-making of airport runway construction projects.
-
Key words:
- airport runway /
- construction scheme optimization /
- improved genetic algorithm /
- construction period /
- quality /
- cost
-
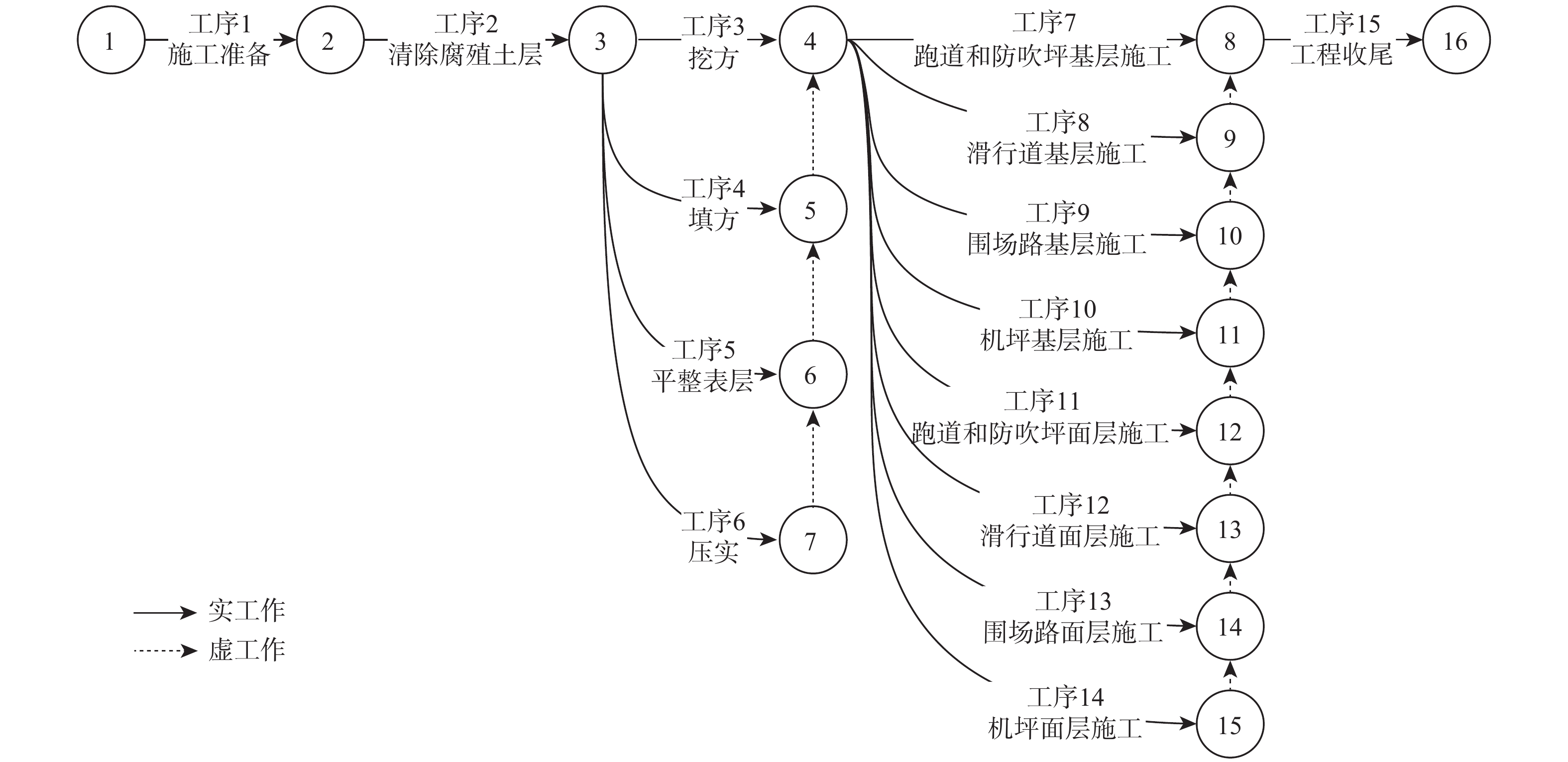
表 1 机场场道施工工序
Table 1. Airport runway construction schedule
过程编号 施工过程 工序名称 工序序号 1 施工准备 施工准备 1 2 土石方工程 清除腐殖土层 2 挖方 3 填方 4 平整表层 5 压实 6 3 基层施工 跑道和防吹坪基层施工 7 滑行道基层施工 8 围场路基层施工 9 机坪基层施工 10 4 面层施工 跑道和防吹坪面层施工 11 滑行道面层施工 12 围场路面层施工 13 机坪面层施工 14 5 工程收尾 工程收尾 15 表 2 机场场道施工优化目标
Table 2. Optimization objective of airport runway construction
目标 优化内容 目标1 成本和质量控制在一定范围内的前提下,工期达到最短 目标2 工期和质量控制在一定范围内的前提下,施工的总成本最小 目标3 工期和成本控制在一定范围内的前提下,施工的质量最高 表 3 施工方案参数
Table 3. Construction scheme parameters
工序序号 施工方案序号 工期/天 直接成本/元 间接成本/元 施工质量 1 1 7 5314 1362 7.8 2 8 4998 1567 8.7 3 6 1432 1032 5.6 2 1 10 9581 2682 8.0 2 7 10321 2032 7.6 3 5 4500 3210 6.8 3 1 100 69431 33162 8.2 2 108 65046 41537 9.5 4 1 60 577 165 7.7 2 70 480 210 9.7 5 1 48 577 160 6.8 2 55 605 231 9.2 6 1 28 8861 2163 8.6 2 35 8135 3263 9.3 7 1 53 368716 98005 8.2 2 62 356351 110236 7.8 8 1 39 387752 63165 7.8 2 43 366547 67533 9.1 9 1 14 55654 9856 8.3 2 18 51328 11246 8.9 10 1 33 386321 103256 8.5 2 36 364110 136142 9.6 11 1 136 208650 62081 8.5 2 145 183865 120115 9.1 12 1 74 243706 52056 6.8 2 80 231596 68449 9.1 13 1 44 37846 11365 7.5 2 49 35625 14025 9.2 14 1 114 186455 81135 8.6 2 126 175343 98741 9.1 15 1 14 4782 1452 8.7 2 15 5028 1765 9.2 表 4 软件运行参数
Table 4. Operating parameters of software
参数 数值 种群规模 1000 进化代数 200 实数编码长度 10 二进制编码长度 20 交叉概率 0.8 变异概率 0.06 最大成本/104元 250 最低质量 8.0 表 5 最优施工方案
Table 5. Optimal construction scheme
施工工序序号 最优施工方案序号 1 3 2 3 3 1 4 2 5 2 6 2 7 1 8 2 9 2 10 1 11 1 12 1 13 2 14 2 15 1 表 6 最优施工方案的工期、成本与质量
Table 6. Period, cost, and quality of optimal construction scheme
施工工期/d 施工成本/元 施工质量 261 2475104 8.4 -
[1] 贾宏, 周波, 刘广兵. 基于层次分析法的风险模型优势分析[J]. 西南交通大学学报, 2009, 44(1): 72-76. doi: 10.3969/j.issn.0258-2724.2009.01.014JIA H, ZHOU B, LIU G B. Advantage analysis of risk model based on analytic hierarchy process[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 72-76(in Chinese). doi: 10.3969/j.issn.0258-2724.2009.01.014 [2] 王维博, 冯全源. 基于改进粒子群算法的工程项目综合优化[J]. 西南交通大学学报, 2011, 46(1): 76-83. doi: 10.3969/j.issn.0258-2724.2011.01.012WANG W B, FENG Q Y. Synthesis optimization for construction project based on modified particle swarm optimization algorithm[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 76-83(in Chinese). doi: 10.3969/j.issn.0258-2724.2011.01.012 [3] 何英, 唐晓宇, 彭亮, 等. 南疆丰收灌区水资源多目标优化配置方案优选[J]. 农业工程学报, 2021, 37(6): 117-126. doi: 10.11975/j.issn.1002-6819.2021.06.015HE Y, TANG X Y, PENG L, et al. Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(6): 117-126(in Chinese). doi: 10.11975/j.issn.1002-6819.2021.06.015 [4] 鲍劲松, 李志强, 周亚勤. 基于遗传算法的舰载装备多目标作业调度优化研究[J]. 系统仿真学报, 2019, 31(5): 901-908.BAO J S, LI Z Q, ZHOU Y Q. Multi-objective operation scheduling optimization of shipborne-equipment based on genetic algorithm[J]. Journal of System Simulation, 2019, 31(5): 901-908(in Chinese). [5] BERTHAUT F, PELLERIN R, PERRIER N, et al. Time-cost trade-offs in resource-constraint project scheduling problems with overlapping modes[J]. International Journal of Project Organisation and Management, 2014, 6(3): 215-236. doi: 10.1504/IJPOM.2014.065259 [6] GWAK H S, SON S H, PARK Y J, et al. Exact time–cost tradeoff analysis in concurrency-based scheduling[J]. Journal of Construction Engineering and Management, 2016, 142(10): 04016054. doi: 10.1061/(ASCE)CO.1943-7862.0001164 [7] FENG X, YAO Y P, LI R N, et al. Loading–unloading judgement for advanced plastic UH model[J]. Acta Mechanica Sinica, 2020, 36(4): 827-839. doi: 10.1007/s10409-020-00936-5 [8] AMINBAKHSH S, SONMEZ R. Pareto front particle swarm optimizer for discrete time-cost trade-off problem[J]. Journal of Computing in Civil Engineering, 2017, 31(1): 04016040. doi: 10.1061/(ASCE)CP.1943-5487.0000606 [9] EL-KHOLY A M. Time–cost tradeoff analysis considering funding variability and time uncertainty[J]. Alexandria Engineering Journal, 2013, 52(1): 113-121. doi: 10.1016/j.aej.2012.07.007 [10] 谢存仁, 徐峰, 阮敏浩. 基于BIM与遗传算法的建筑工程施工进度多目标优化研究[J]. 工程管理学报, 2021, 35(3): 117-122.XIE C R, XU F, RUAN M H. Study on multi-objective optimization of construction schedule based on BIM and genetic algorithm[J]. Journal of Engineering Management, 2021, 35(3): 117-122(in Chinese). [11] 马聪聪. 基于改进遗传算法的地铁施工项目多目标优化[D]. 兰州: 兰州交通大学, 2020.MA C C. Multi-objective optimization of subway construction project based on improved genetic algorithm[D]. Lanzhou: Lanzhou Jiatong University, 2020(in Chinese). [12] 中国民用航空局. 2020年民航行业发展统计公报[EB/OL]. (2021-06-10)[2022-10-15]. https://www.gov.cn/xinwen/2021-06/10/content_5616880.htm.Civil Aviation Administration of China. Statistical bulletin of civil aviation industry development in 2020[EB/OL]. (2021-06-10)[2022-10-15]. https://www.gov.cn/xinwen/2021-06/10/content_5616880.htm(in Chinese). [13] 李汝宁, 何勇灵. 基于遗传算法的柴油机喷油系统模型参数辨识[J]. 北京航空航天大学学报, 2012, 38(4): 464-467.LI R N, HE Y L. Parameter identification of diesel fuel injection system model using genetic algorithms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 464-467(in Chinese). [14] 冯兴, 李汝宁, 安然, 等. 基于节能的机场飞行区平面布局优化[J]. 中国民航大学学报, 2016, 34(2): 27-31. doi: 10.3969/j.issn.1674-5590.2016.02.007FENG X, LI R N, AN R, et al. Plane layout optimization of airport flight area based on energy conservation[J]. Journal of Civil Aviation University of China, 2016, 34(2): 27-31(in Chinese). doi: 10.3969/j.issn.1674-5590.2016.02.007 [15] 单宝英, 郭萍, 张帆, 等. 基于遗传算法与方案优选的多目标优化模型求解方法[J]. 中国农业大学学报, 2019, 24(6): 157-165. doi: 10.11841/j.issn.1007-4333.2019.06.18SHAN B Y, GUO P, ZHANG F, et al. A multi-objective optimization model solving method based on genetic algorithm and scheme evaluation[J]. Journal of China Agricultural University, 2019, 24(6): 157-165(in Chinese). doi: 10.11841/j.issn.1007-4333.2019.06.18 [16] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 [17] DEB K, ANAND A, JOSHI D. A computationally efficient evolutionary algorithm for real-parameter optimization[J]. Evolutionary Computation, 2002, 10(4): 371-395. doi: 10.1162/106365602760972767 [18] 辛宇, 童孟军, 华宇婷. 一种基于最优特征选择改进的遗传算法[J]. 传感技术学报, 2018, 31(11): 1747-1752. doi: 10.3969/j.issn.1004-1699.2018.011.022XIN Y, TONG M J, HUA Y T. An improved genetic algorithm based on optimal feature selection[J]. Chinese Journal of Sensors and Actuators, 2018, 31(11): 1747-1752(in Chinese). doi: 10.3969/j.issn.1004-1699.2018.011.022 [19] DEHGHAN R, HAZINI K, RUWANPURA J. Optimization of overlapping activities in the design phase of construction projects[J]. Automation in Construction, 2015, 59: 81-95. doi: 10.1016/j.autcon.2015.08.004 [20] HAZINI K, DEHGHAN R, RUWANPURA J. A heuristic method to determine optimum degree of activity accelerating and overlapping in schedule compression[J]. Canadian Journal of Civil Engineering, 2013, 40(4): 382-391. doi: 10.1139/cjce-2012-0380 [21] SROUR I M, ABDUL-MALAK M A U, YASSINE A A, et al. A methodology for scheduling overlapped design activities based on dependency information[J]. Automation in Construction, 2013, 29: 1-11. doi: 10.1016/j.autcon.2012.08.001 -







 下载:
下载: