基于CFD/CSD耦合的高速射弹尾拍载荷特性研究

许云涛; 檀大林; 杨超

doi:10.13700/j.bh.1001-5965.2022.0939

基于CFD/CSD耦合的高速射弹尾拍载荷特性研究

doi: 10.13700/j.bh.1001-5965.2022.0939

许云涛^{1, 2},
檀大林²,
杨超^1, ,

1.
北京航空航天大学航空科学与工程学院，北京 100191
2.
北京机电工程研究所，北京 100074

详细信息

通讯作者:
E-mail：yangchao@buaa.edu.cn

中图分类号: TJ630
计量
- 文章访问数: 248
- HTML全文浏览量: 80
- PDF下载量: 20
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-24
- 录用日期: 2023-02-26
- 网络出版日期: 2023-04-03
- 整期出版日期: 2023-10-01

Study on tail-slap load characteristics of high-speed projectile based on CFD/CSD coupling

XU Yuntao^{1, 2},
TAN Dalin²,
YANG Chao^{1
, ,}

1.
School of Aeronautic Science and Engineering，Beihang University，Beijing 100191，China
2.
Beijing Institute of Mechanical and Electrical Engineering，Beijing 100074，China

More Information

Corresponding author: E-mail：yangchao@buaa.edu.cn

摘要

摘要:
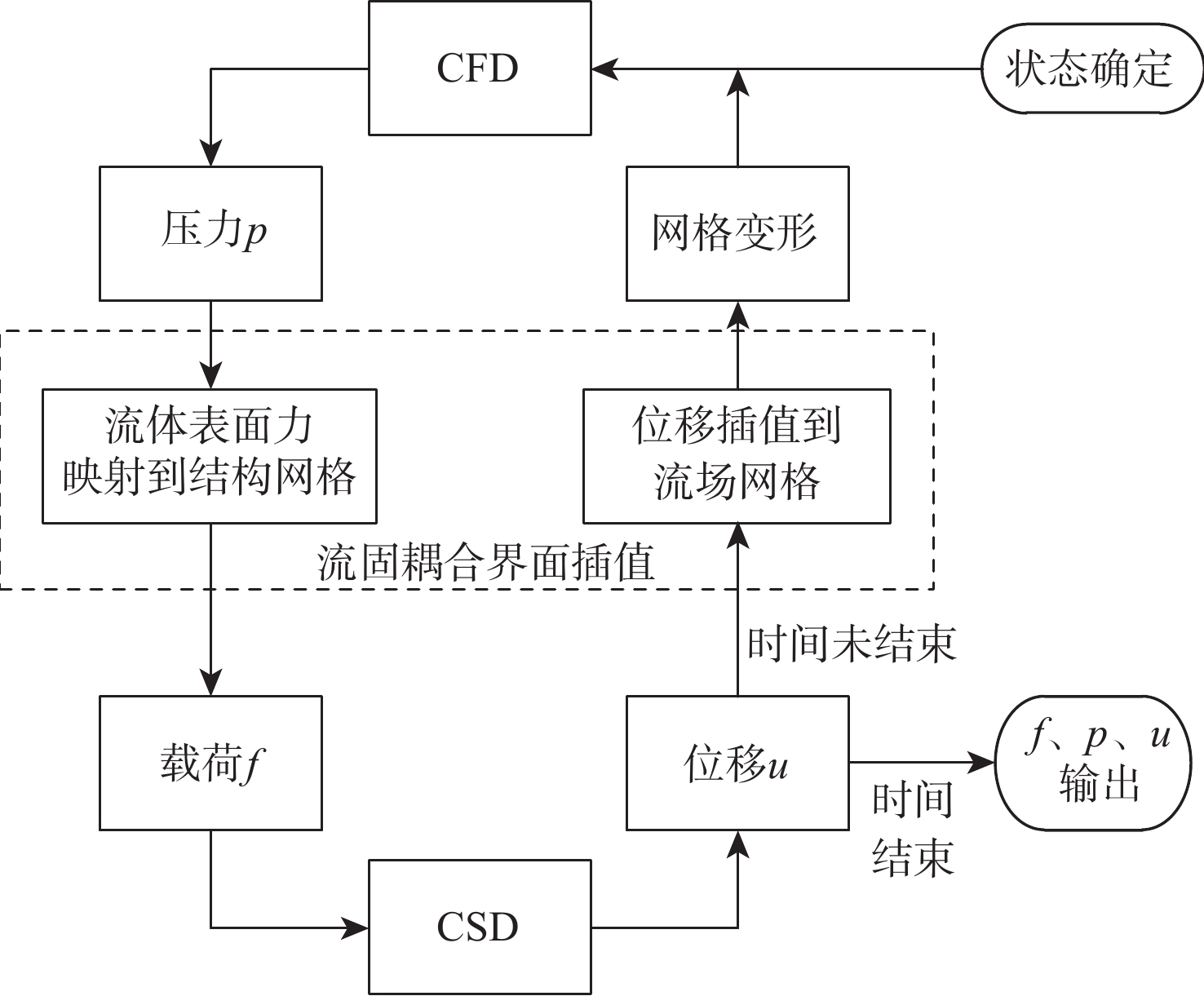
为提高射弹尾拍载荷的预测精度，建立了一套基于计算流体动力学（CFD）/计算结构动力学（CSD）双向耦合分析的计算方法和程序。射弹流体计算主控方程采用耦合SSTk-ω湍流模型和Schnerr-Sauer空化模型的Navier-Stokes方程，射弹结构计算采用基于模态叠加法简化的结构动力学方程，流固耦合界面插值采用径向基函数法，网格变形采用弹簧网格法。分别对泡型计算方法和流固耦合方法进行验证，在此基础上，计算对比1 000 m/s速度下射弹刚体和弹性体的尾拍泡型、结构变形和尾拍流体载荷特性差异。计算表明：弹性体尾拍过程，射弹泡型会产生弹身“二次拍击”、“局部沾湿”和沾湿面积增大等特殊现象，结构变形由弹性一弯模态主导，较大的变形引起流体载荷增大27%~105%，尾拍姿态角增大13%，尾拍频率增加20%，流固耦合效应对尾拍泡型、尾拍载荷和尾拍弹道均产生了较强的影响。
- 射弹 /
- CFD/CSD耦合 /
- 尾拍 /
- 载荷 /
- 刚体 /
- 弹性体
Abstract:
A calculating approach based on the two-way analysis of computational fluid dynamics (CFD)/computational structure dynamics (CSD) coupling is devised to increase the predictability of the projectile’s tail-slap load. The main governing equation of fluid calculation adopts the Navier-Stokes equation with SST k-ω turbulent flow model and Schnerr-Sauer cavitation model, structural calculations use simplified structural dynamic equations based on the modal superposition method, interpolation of fluid-structural coupling interface using radial basis function method, mesh deformation using spring stretching method. Both the fluid-structural coupling approach and the cavity shape computation method were independently verified. Further, the differences in cavity shape, structural deformation, and characteristics of tail-slap loads between the rigid body and the elastic body of the projectile at a speed of 1000 m/s were calculated and compared. Simulation results show that during the tail-slapping process of the elastic body, the cavity shape of the projectile will produce special phenomena such as ‘secondary slap’, ‘partial wetting’ and a wetting area increased. Structural deformation is dominated by the first-bending mode. The larger deformation causes the dynamic load to increase by 27%~105%, the amplitude of the pitch angle to increase by 13%, and the tail-slapping frequency to increase by 20%. The fluid-structural coupling effect has a strong influence on the cavity shape, loads, and ballistic of tail-slapping.
- projectile /
- CFD/CSD coupling /
- tail-slap /
- load /
- rigid body /
- elastic body

HTML全文

图 1 CFD/CSD双向流固耦合迭代流程

Figure 1. Two-way CFD/CSD fluid-structural coupling iterative process

下载: 全尺寸图片幻灯片

图 2 本文泡型与试验数据及经验公式对比

Figure 2. Comparison of cavity shape in this paper with experimental data and empirical formula

下载: 全尺寸图片幻灯片

图 3 广义位移时间曲线(Ma = 0.96)

Figure 3. Curves of generalized displacement time (Ma = 0.96)

下载: 全尺寸图片幻灯片

图 4 超空泡射弹模型

Figure 4. Model of supercavitating projectile

下载: 全尺寸图片幻灯片

图 5 流体计算域及边界条件示意图

Figure 5. Schematic diagram of fluid calculation domain and boundary conditions

下载: 全尺寸图片幻灯片

图 6 流场网格无关性分析

Figure 6. Independent analysis of flow field mesh

下载: 全尺寸图片幻灯片

图 7 流场网格模型

Figure 7. Mesh of flow field

下载: 全尺寸图片幻灯片

图 8 结构网格模型

Figure 8. Mesh of structural model

下载: 全尺寸图片幻灯片

图 9 3阶弹性模态

Figure 9. First three order elastic modes

下载: 全尺寸图片幻灯片

图 10 刚体与弹性体尾拍运动泡型对比

Figure 10. Comparison of cavity profiles between rigid body and elastic body during tail-slapping

下载: 全尺寸图片幻灯片

图 11 典型节点y向变形的峰值分布

Figure 11. Distribution of peak deformation of typical nodes

下载: 全尺寸图片幻灯片

图 12 刚体与弹性体尾拍流体载荷及俯仰角对比

Figure 12. Comparisons of loads and pitch angle between rigid body and elastic body during tail-slapping

下载: 全尺寸图片幻灯片

表 1 超空泡射弹材料参数

Table 1. Material parameters of supercavitating projectile

部位	材料	弹性模量/GPa	密度/(kg·m⁻³)	泊松比
锥段	钨合金	312	17 500	0.3
柱段	钢	210	7 850	0.3

下载: 导出CSV

表 2 刚体与弹性体尾拍流体载荷特性对比

Table 2. Comparison of load characteristics between rigid body and elastic body during tail-slapping

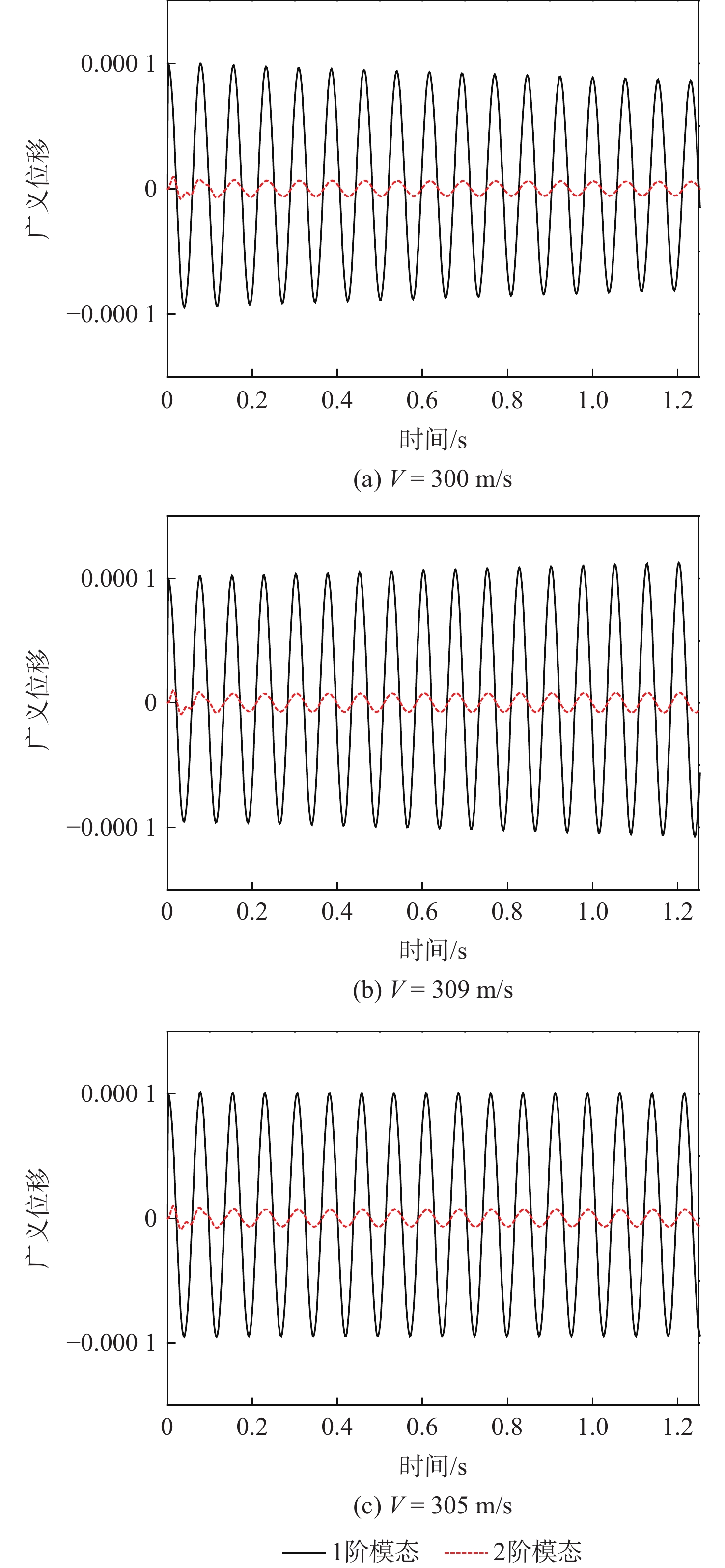
类型	尾拍引起的轴向力增量峰值/kN	尾拍法向力峰值/kN	俯仰力矩峰值/(kN·m)	尾拍姿态角峰值/(°)	尾拍频率/Hz
刚体	1.35	4.21	0.21	5.83	329
弹性体	1.72	6.95	0.43	6.59	394
变化量	0.37	2.74	0.22	0.76	65
注：尾拍引起的轴向力增量峰值、尾拍法向力峰值、俯仰力矩峰值、尾拍姿态角峰值、尾拍频率的变化百分比分别为27%，65%，105%，13%，20%。

下载: 导出CSV

参考文献(23)

[1]	潘森森, 彭晓星. 空化机理[M]. 北京: 国防工业出版社, 2013. PAN S S, PENG X X. Physical mechanism of cavitation[M]. Beijing: National Defense Industry Press, 2013(in Chinese).
[2]	熊天红, 易文俊. 高速射弹超空泡减阻试验研究与数值模拟分析[J]. 工程力学, 2009, 26(8): 174-178. XIONG T H, YI W J. Experimental research and numerical simulation of supercavity drag reduction of a high speed projectile[J]. Engineering Mechanics, 2009, 26(8): 174-178(in Chinese).
[3]	曹伟, 魏英杰, 王聪, 等. 超空泡技术现状、问题与应用[J]. 力学进展, 2006, 36(4): 571-579. CAO W, WEI Y J, WANG C, et al. Current status, problems and applications of supercavitation technology[J]. Advances in Mechanics, 2006, 36(4): 571-579(in Chinese).
[4]	杨莉, 张庆明. 超空泡技术的应用现状和发展趋势[J]. 战术导弹技术, 2006(5): 6-10. doi: 10.3969/j.issn.1009-1300.2006.05.002 YANG L, ZHANG Q M. Current application and perspectives on supercavitation technology research[J]. Tactical Missile Technology, 2006(5): 6-10(in Chinese). doi: 10.3969/j.issn.1009-1300.2006.05.002
[5]	黄闯. 跨声速超空泡射弹的弹道特性研究[D]. 西安: 西北工业大学, 2017. HUANG C. Research of trajectory characteristics of supersonic-supercavitating projectiles[D]. Xi’an: Northwestern Polytechnical University, 2017(in Chinese).
[6]	魏英杰, 何乾坤, 王聪, 等. 超空泡射弹尾拍问题研究进展[J]. 舰船科学技术, 2013, 35(1): 7-15. WEI Y J, HE Q K, WANG C, et al. Review of study on the tail-slap problems of supercavitating projectile[J]. Ship Science and Technology, 2013, 35(1): 7-15(in Chinese).
[7]	郝常乐, 党建军, 陈长盛, 等. 基于双向流固耦合的超空泡射弹入水研究[J]. 力学学报, 2022, 54(3): 678-687. HAO C L, DANG J J, CHEN C S, et al. Numerical study on water entry process of supercavitating projectile by considering bidirectional fluid structure interaction effect[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 678-687(in Chinese).
[8]	CHEN C, ZHANG A M, CHEN J Q, et al. SPH simulations of water entry problems using an improved boundary treatment[J]. Ocean Engineering, 2021, 238: 109679. doi: 10.1016/j.oceaneng.2021.109679
[9]	LI Y, SUN T Z, ZONG Z, et al. Dynamic crushing of a dedicated buffer during the high-speed vertical water entry process[J]. Ocean Engineering, 2021, 236: 109526. doi: 10.1016/j.oceaneng.2021.109526
[10]	张劲生. 超空泡运动体尾拍冲击振动特性的研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. ZHANG J S. Research on impact and vibration characteristic of supercavitating high-speed bodies with tail-slaps[D]. Harbin: Harbin Institute of Technology, 2010(in Chinese).
[11]	梁景奇, 王瑞, 徐保成, 等. 攻角对高速射弹入水过程影响研究[J]. 兵器装备工程学报, 2020, 41(7): 23-28. doi: 10.11809/bqzbgcxb2020.07.006 LIANG J Q, WANG R, XU B C, et al. Research on influence of angle of attack on process of high-speed water-entry projectile[J]. Journal of Ordnance Equipment Engineering, 2020, 41(7): 23-28(in Chinese). doi: 10.11809/bqzbgcxb2020.07.006
[12]	王强, 侯宇, 金子涵, 等. 基于双向流固耦合的柔性扑翼变形数值研究[J]. 飞行力学, 2021, 39(3): 27-33. WANG Q, HOU Y, JIN Z H, et al. Numerical study on the deformation of flexible flapping wing based on bidirectional fluid-solid coupling[J]. Flight Dynamics, 2021, 39(3): 27-33(in Chinese).
[13]	秦杨, 易文俊, 管军. 超空泡射弹高速倾斜入水的空化流动数值模拟[J]. 兵器装备工程学报, 2019, 40(7): 99-104. doi: 10.11809/bqzbgcxb2019.07.020 QIN Y, YI W J, GUAN J. Numerical simulation for cavitation flow of high-speed rotating body oblique entrying into water[J]. Journal of Ordnance Equipment Engineering, 2019, 40(7): 99-104(in Chinese). doi: 10.11809/bqzbgcxb2019.07.020
[14]	MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. doi: 10.2514/3.12149
[15]	谢亮, 徐敏, 李杰, 等. 基于CFD/CSD耦合的颤振与动载荷分析方法[J]. 振动与冲击, 2012, 31(3): 106-110. doi: 10.3969/j.issn.1000-3835.2012.03.022 XIE L, XU M, LI J, et al. Flutter and dynamic analysis based on CFD/CSD coupling method[J]. Journal of Vibration and Shock, 2012, 31(3): 106-110(in Chinese). doi: 10.3969/j.issn.1000-3835.2012.03.022
[16]	许云涛, 吴志刚, 杨超. 地面颤振模拟试验中的非定常气动力模拟[J]. 航空学报, 2012, 33(11): 1947-1957. XU Y T, WU Z G, YANG C. Simulation of the unsteady aerodynamic forces for ground flutter simulation test[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 1947-1957(in Chinese).
[17]	林言中, 陈兵, 徐旭. 基于径向基函数插值的气动弹性计算方法[J]. 北京航空航天大学学报, 2014, 40(7): 953-958. doi: 10.13700/j.bh.1001-5965.2013.0460 LIN Y Z, CHEN B, XU X. Numerical method of aeroelasticity based on radial basis function interpolation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 953-958(in Chinese). doi: 10.13700/j.bh.1001-5965.2013.0460
[18]	周璇, 李水乡, 陈斌. 非结构动网格生成的弹簧-插值联合方法[J]. 航空学报, 2010, 31(7): 1389-1395. ZHOU X, LI S X, CHEN B. Spring-interpolation approach for generating unstructured dynamic meshes[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1389-1395(in Chinese).
[19]	HRUBES J D. High-speed imaging of supercavitating underwater projectiles[J]. Experiments in Fluids, 2001, 30(1): 57-64. doi: 10.1007/s003480000135
[20]	陈伟善. 高速超空泡射弹尾拍运动特性数值研究[D]. 南京: 南京理工大学, 2020. CHEN W S. Numerical study on the motion characteristics of the tail-slap of the high-speed supercavitating projectile[D]. Nanjing: Nanjing University of Science and Technology, 2020(in Chinese).
[21]	罗格维诺维奇. 自由边界流动的水动力学[M]. 施红辉译. 上海: 上海交通大学出版社, 2012: 97-126. LOGVINOVICH G V. Hydrodynamics of free-boundary flow[M]. SHI H H, translated. Shanghai: Shanghai Jiao Tong University Press, 2012: 97-126(in Chinese).
[22]	SAVCHENKO Y N. Supercavitation-problems and perspectives[C]// 4th International Symposium on Cavitation, 2001: 1-8.
[23]	JK YATES E C. AGARD standard aeroelastic configuration for dynamic response I-wing-445.6: NASA-TM-100492[R]. Washington, D. C. :NASE, 1988.