Double light curtain-constrained hazy image restoration algorithm based on improved atmospheric scattering model
-
摘要:
当雾霾退化场景处于光照不均匀的条件下时，部分场景细节不仅会由于雾气遮盖导致可见度降低，同时会因为光照阴影使得部分区域不可见。针对这一问题，提出一种基于改进型大气散射模型的双光幕边界约束的雾天图像复原算法。分析传统大气散射模型的成像原理，利用其退化机理结合Retinex理论对模型进行改进；引入均值不等关系与高斯衰减函数，通过预估特征值的方法对大气光幕进行估计，并设定上下边界对其进行约束；依照改进型大气散射模型求取场景入射光，并利用亮通道先验求取有雾图像亮通道对场景入射光进行补偿；改进局部大气光的获取方法，提出基于中通道的局部大气光估计方法，结合所求大气光幕与场景入射光代入改进型大气散射模型获得无雾图像，并使其与图像纹理层进行融合得到最终的复原结果。根据对实验结果的定性与定量分析，所提算法不仅可以有效复原出场景光照不均的有雾图像，针对其余场景下的雾霾场景也可得到较好的复原效果，且复原场景清晰，明亮度适宜。
Abstract:When a haze-degraded scene is under uneven lighting conditions, some scene details will be less visible due to hazy obscuration and light shadows. To address this issue, a hazy image restoration algorithm with double light curtain boundary constraints based on an improved atmospheric scattering model was proposed. The imaging principle of the conventional atmospheric scattering model was analyzed, and the model was improved by using its degradation mechanism combined with the Retinex theory. The mean inequality relation and Gaussian decay function were introduced to estimate the eigenvalue of the atmospheric light curtain. In addition, the upper and lower boundaries were set to constrain the estimated values. The scene-incident light was obtained by an improved atmospheric scattering model, which was compensated by using the bright channel of the hazy image through the bright channel prior method. The method of local atmospheric light acquisition was improved. A mid-channel-based local atmospheric light estimation method was proposed. The estimated atmospheric light curtain and scene-incident light were introduced into an improved atmospheric scattering model to obtain a hazy-free image. Then, the hazy-free image was fused with the image texture layer to obtain the final restored image. According to the subjective and objective analyses of the experimental results, the proposed algorithm can not only effectively restore the hazy images with uneven scene illumination but also get a better restoration effect for the haze scenes. The restored scene is clear, and the brightness is moderate.
-
雾、霾的形成是由于大气中含有大量的悬浮介质导致光线产生散射或吸收作用，使得视觉能见度降低，如细小水滴、气溶胶、沙尘等颗粒。这种天气现象会使得一些图像及视频采集设备呈现低对比度、色彩偏移、细节丢失等问题，对计算机视觉领域的相关任务造成严重的影响。因此，雾天场景的清晰化复原具有重要的实际意义和研究价值。
目前去雾领域大致可分为图像增强、图像复原和神经网络这3类方法[1]。基于图像增强[2-4]是较为早期的方法，此类方法虽能增强或削弱图像中需要与不需要的信息，但未考虑图像退化的本质，使得最终的去雾效果无法达到预期要求，代表性方法有直方图均衡化[2]、同态滤波[3]和Retinex理论[4]等。
利用图像复原[5-8]是去雾领域中较为传统的一种方法，该系列方法主要是依据大气散射模型进行相应的去雾处理，从图像的退化本质出发，通过对先验知识进行假设来达到估计参数的目的，从而完成对雾图的清晰化处理。文献[5]提出暗通道先验方法，通过对大量雾图研究发现大多数雾图的暗通道值趋于0，间接利用消元的方法对大气散射模型进行化简，以得出参数，但该方法并未考虑到含有天空区域的雾天场景，由于天空区域的暗通道值并不为0，导致暗通道先验失效，使得含天空区域雾图复原结果颜色失真严重；文献[6]提出一种颜色衰减先验方法，利用图像的亮度与饱和度信息建立一种与场景深度相关的线性关系，进而得出无雾图像，但其大气散射系数选取较为单一，透射率估计过大，容易产生去雾不彻底的现象；文献[7]设计了一种分段函数，利用其代替最小值滤波操作，避免了复原结果出现光晕效应，但该方法在一定程度上存在去雾不彻底的问题；文献[8]提出一种基于伽马校正先验的去雾方法，该方法从原始雾图和均匀虚拟转换中提取深度比，再采用全局策略和视觉指示器来恢复场景反照率，但该方法存在估计误差，会导致复原结果出现光晕伪影。
以上方法均是基于传统大气散射模型对雾图进行复原，虽然能在一定程度上达到去雾的效果，但由于传统的大气散射模型未考虑到场景入射光照的影响，因此，在复原过程中，对光照不均匀区域产生的阴影部分并不能得到一个很好的复原效果。
此外，近年来由于神经网络在一些任务上取得了不俗的进展，相关的研究也逐渐运用到了去雾领域上[9-13]。该类方法大致可分为端到端与非端到端2类。文献[9]提出一体化多合一去雾网络，该网络将大气散射模型中的多个未知参数合并为一个进行训练，从而得到无雾图像；文献[10]建立了多个不同尺度的网络模型，利用这种多尺度网络学习雾图与透射率之间所存在的映射关系；文献[11]提出一种仿射双边网络，通过多引导双边学习高清图像的方法，仿射图像的高质量特征，以此达到去雾的目的；文献[12]通过直接学习原图与雾图之间的残差，提出一种门控语境聚合网络；文献[13]提出一种基于渐进特征融合的U-Net网络，可以不依赖大气散射模型直接学习有雾图像和无雾图像之间的高度非线性变换函数。
由于深度学习类方法处理有雾图像时缺少大量真实的场景图进行训练，使用的大多是合成图像，因此，此类方法去雾效果不稳定，在部分真实场景下易产生去雾不彻底的情况。
本文针对传统大气散射模型未考虑场景入射光，导致阴影部分难以复原的问题，提出一种改进型大气散射模型的双光幕边界约束的雾天图像复原算法，并引入均值不等关系对大气光幕进行上下边界约束，使得复原结果适应多种不同场景条件。实验结果表明，本文算法不仅去雾彻底，且对光照不均匀区域的阴影部分也能实现较好的复原效果。
1. 相关背景
1.1 大气散射模型
在数字图像处理及计算机视觉领域中，常用大气散射模型来阐述雾天图像的成像机理，即
I(x,y)=J(x,y)t(x,y)+A(x,y)[1−t(x,y)]=A(x,y)ρ(x,y)t(x,y)+A(x,y)[1−t(x,y)] (1) 式中：$ (x,y) $为像素坐标；$ {{\boldsymbol{I}}}(x,y) $为有雾图像；$ {{\boldsymbol{J}}}(x,y) $为无雾图像；$ {{\boldsymbol{A}}}(x,y) $为大气光值；$ {{\boldsymbol{\rho }}}(x,y) $为场景反照率；$ {{\boldsymbol{t}}}(x,y) $为透射率，当场景中的大气悬浮粒子分布较为均匀时，透射率$ {{\boldsymbol{t}}}(x,y) $可表示为
t(x,y)=exp(−βd(x,y)) (2) 式中：$ \beta $为大气散射系数；$ {{\boldsymbol{d}}}(x,y) $为景深。
模型中$ {{\boldsymbol{A}}}(x,y) $与$ {{\boldsymbol{t}}}(x,y) $为未知参量，$ {{\boldsymbol{J}}}(x,y) $或$ {{\boldsymbol{\rho}} }(x,y) $为待估计参量。在大气散射模型中$ {{\boldsymbol{J}}}(x,y){{\boldsymbol{t}}}(x,y) $为直接传输项，表示大气中悬浮的散射介质粒子经场景辐射后的衰减过程。$ {{\boldsymbol{A}}}(x,y)[1 - {{\boldsymbol{t}}}(x,y)] $为大气光幕，表示大气中的散射光，定义为$ {{\boldsymbol{V}}}(x,y) $，且满足：
{V(x,y)⩽ (3) 式中：$ {{\boldsymbol{W}}}(x,y) $为有雾图像的最小通道；$ c\in\{{\mathrm{red}}, {\mathrm{green}}, {\mathrm{blue}}\} $代表RGB三通道[14]。
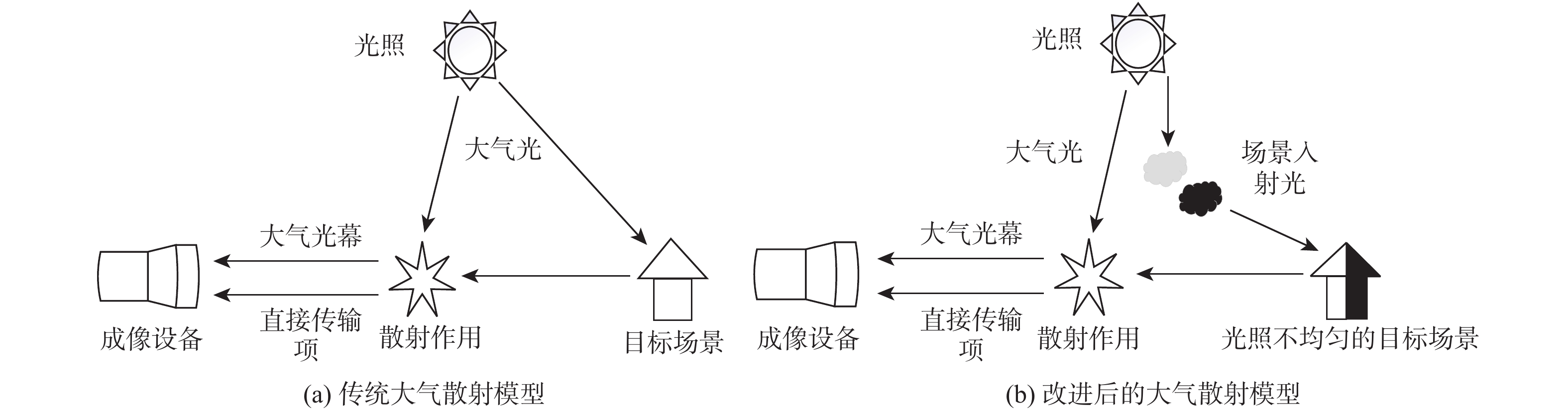
1.2 大气散射模型的不足
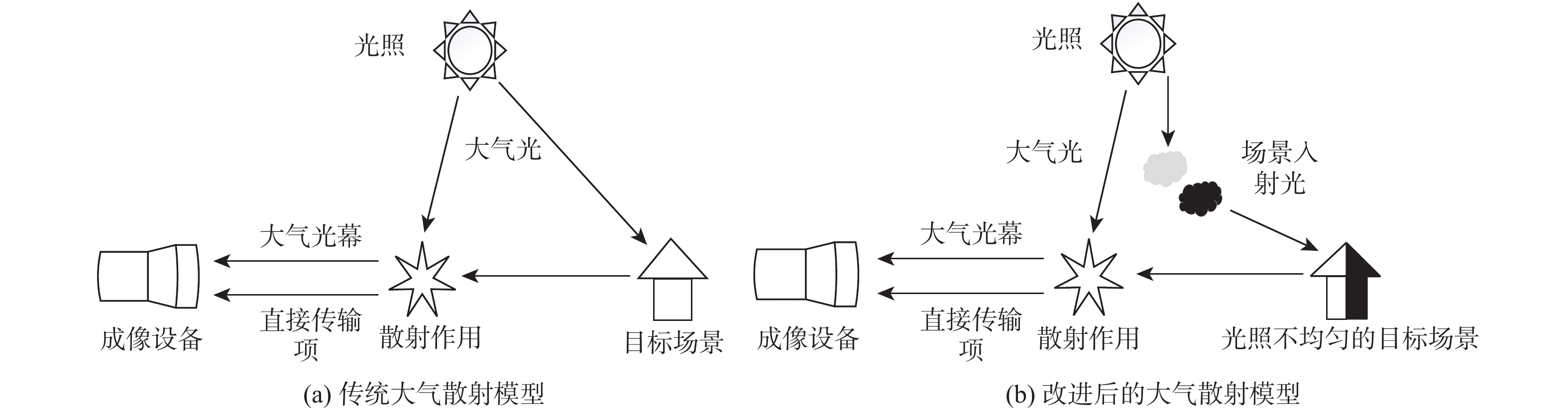
根据传统的大气散射模型对直接传输项与大气光幕的定义，图像的退化原因一般具有3个因素，分别为雾霾对照射目标过程的光源的光谱散射引起的成像质量的原始退化、目标反射光到成像系统在传输路径上的光谱的散射衰减退化、直接进入成像系统的雾霾散射光噪声引起的图像退化[15]。考虑到这些因素，模型中将场景中所有的入射光照定义为大气光这一全局常量其实并不合理，当场景光照不均匀时，大气光幕项中由于所描述的光源未经衰减，所以此时该项传播路径中的粒子大多仍暴露在大气中，可认为全局常量，满足大气光的定义，但在直接传输项中的光源信息应当包括各种反射光与折射光，并非常量。因此，传统大气散射模型中将直接传输项中的光源信息设为恒定的大气光是不合适的。
因此，本文算法拟从场景入射光入手改进传统大气散射模型对直接传输项中光源信息的设定，使得改进后的大气散射模型不仅可以复原一般雾霾场景，针对光源照射不均匀的阴暗区域也可得到较好的复原效果。
2. 本文算法
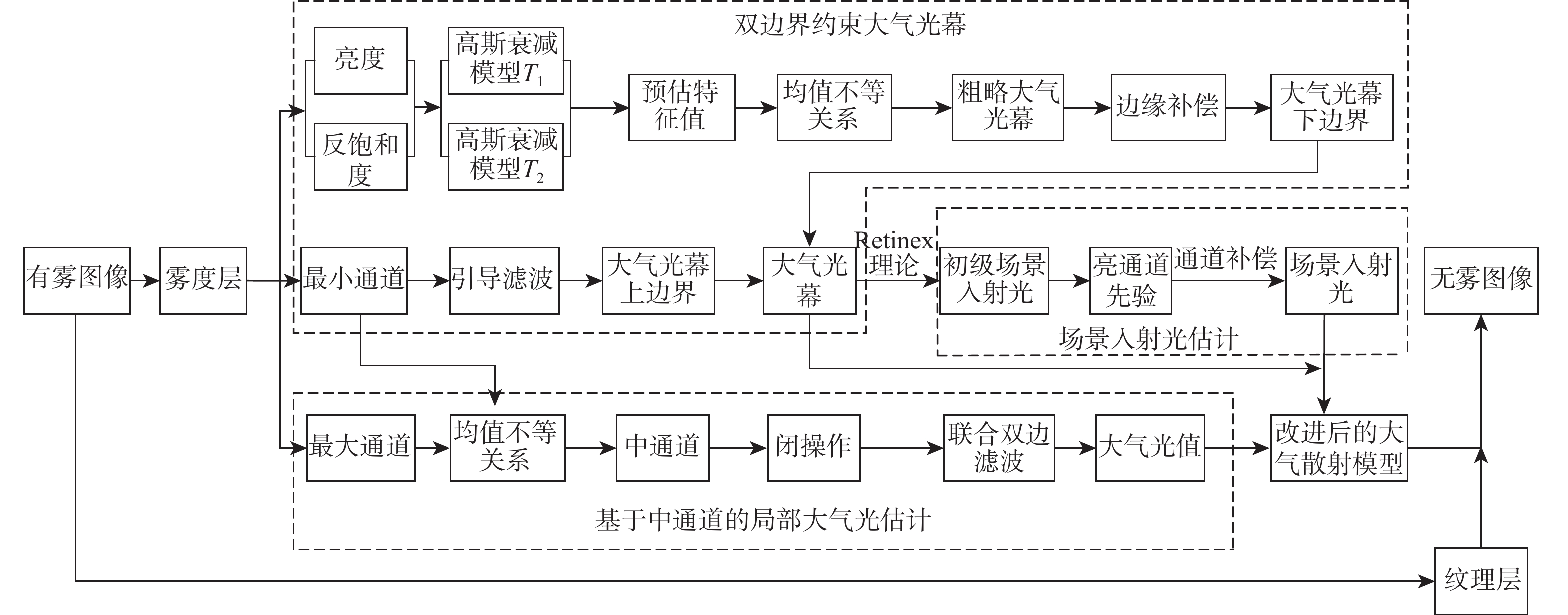
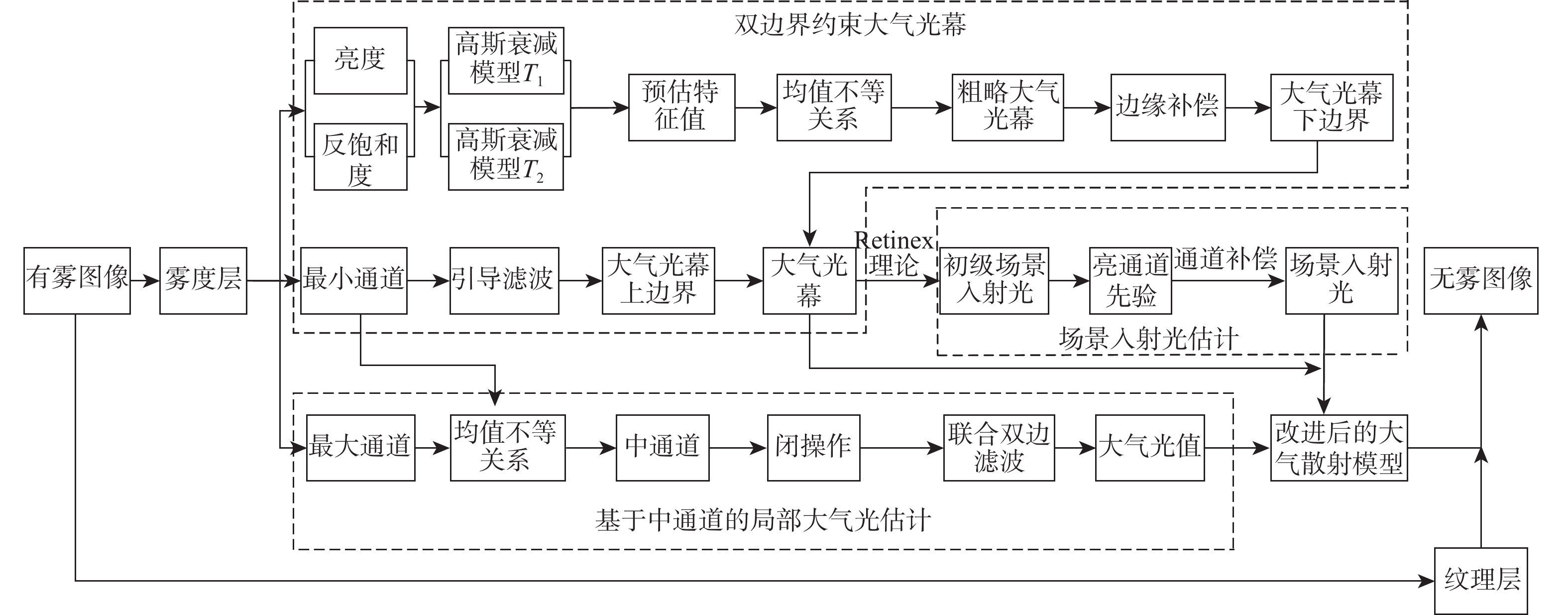
本文通过引入场景入射光对大气散射模型进行改进，使得该模型在处理光照不均匀图像时，不仅可以较大程度的复原有雾图像的细节信息，同时可以提升图像阴暗区域的可见度。并将雾图分为雾度层和纹理层2部分，避免额外信息对复原结果产生影响。针对未知参数的估计，本文结合高斯衰减函数与均值不等关系设定不同的上下边界对大气光幕进行约束与估计，并利用雾图中通道改进局部大气光的获取，本文算法流程如图1所示。
2.1 改进型大气散射模型
文献[16]通过增加噪声光对传统雾天成像的大气散射模型进行改进，但仅考虑了雾霾场景下的人造光源信息，并未考虑到太阳光由于反射或折射造成的场景光照不均匀区域的信息复原。为完善这类问题，本文算法通过分析成像设备所接收光源的主要途径，结合Retinex理论引入场景入射光进一步改进大气散射模型。
Retinex理论的思想是认为人眼视觉感知到的色彩、亮度主要来自于一般场景中的物体反射，而非受光照影响[4]。根据该理论，一幅图像可表示为
{{\boldsymbol{S}}}(x,y) = {{\boldsymbol{R}}}(x,y){{\boldsymbol{L}}}(x,y) (4) 式中：$ {{\boldsymbol{S}}}(x,y) $为原图像；$ {{\boldsymbol{R}}}(x,y) $为反射图像；$ {{\boldsymbol{L}}}(x,y) $为场景入射光，入射光的大小决定了一幅图像其像素所能达到的动态范围，一般用原图像与环绕函数的卷积对其进行估计，表达式为
{{\boldsymbol{L}}}(x,y) = {{\boldsymbol{S}}}(x,y) \otimes F (5) 式中：$ \otimes $表示卷积操作；$ F $为中心环绕函数。
而Retinex理论中对场景入射光的描述恰好满足直接传输项中对光源信息的要求，根据这一推论，本文对传统大气散射模型进行改进。将直接传输项中的大气光$ {{\boldsymbol{A}}}(x,y) $改为场景入射光$ {{\boldsymbol{L}}}(x,y) $，因此，式(1)可改写为
\begin{split} &{{\boldsymbol{I}}}(x,y) = {{\boldsymbol{L}}}(x,y){{\boldsymbol{\rho}} }(x,y){{\boldsymbol{t}}}(x,y) + {{\boldsymbol{A}}}(x,y)[1 - {{\boldsymbol{t}}}(x,y)] =\\ &\quad\quad {{\boldsymbol{L}}}(x,y){{\boldsymbol{\rho }}}(x,y)\left[1 - \frac{1}{{{{\boldsymbol{A}}}(x,y)}}{{\boldsymbol{V}}}(x,y)\right] + {{\boldsymbol{V}}}(x,y) \end{split} (6) 由于Retinex理论在复原有雾图像时考虑到了场景入射光对复原效果的影响，基于这一点，将式(6)改为Retinex的形式，即
{{{\boldsymbol{S}}}_{{\text{new}}}}(x,y) = {{{\boldsymbol{R}}}_{{\text{new}}}}(x,y){{{\boldsymbol{L}}}_{{\text{new}}}}(x,y) (7) 式(7)中各个参数的表达式为
\left\{ \begin{aligned} &{{{{\boldsymbol{S}}}_{{\text{new}}}}(x,y) = {{\boldsymbol{I}}}(x,y) - {{\boldsymbol{V}}}(x,y)} \\ & {{{{\boldsymbol{R}}}_{{\text{new}}}}(x,y) = \left[1 - \frac{1}{{{{\boldsymbol{A}}}(x,y)}}{{\boldsymbol{V}}}(x,y)\right]{{\boldsymbol{\rho}} }(x,y)} \\ &{{{{\boldsymbol{L}}}_{{\text{new}}}}(x,y) = {{\boldsymbol{L}}}(x,y)} \end{aligned} \right. (8) 式中：$ {{{\boldsymbol{S}}}_{{\text{new}}}}(x,y) $为新模型下的原图像；$ {{{\boldsymbol{R}}}_{{\text{new}}}}(x,y) $为新模型下的反射图像；$ {{{\boldsymbol{L}}}_{{\text{new}}}}(x,y) $为场景入射光。改进前后的大气散射模型对比，如图2所示。
图 2 大气散射模型物理退化过程Figure 2. Physical degradation process of atmospheric scattering model此外，为避免在图像复原过程中，可能存在的纹理、噪声等信息对复原结果产生影响，使主观效果不佳。本文将有雾图像$ {{\boldsymbol{I}}}(x,y) $分为雾度层$ {{\boldsymbol{C}}}(x,y) $和纹理层$ {{\boldsymbol{T}}}(x,y) $，雾度层为有雾图像的雾霾与背景等信息，纹理层表示有雾图像的纹理细节、噪声等信息，表达式为
{{\boldsymbol{I}}}(x,y) = {{\boldsymbol{C}}}(x,y) + {{\boldsymbol{T}}}(x,y) (9) 在图像复原过程中，先去除有雾图像纹理层，再按改进型大气散射模型估计各参数，得到初级无雾图像，最终将提取出的纹理层图像与初级无雾图像进行融合得到最终的复原结果。这样即可避免纹理层信息对复原结果造成的干扰，又能使得复原结果更加贴近真实场景，具体参数求取在后续章节进行。
图3为分别基于改进前后2种大气散射模型下的复原结果对比。可以看出，基于改进后的大气散射模型下的复原图像较传统大气散射模型更能复原出有雾图像在光照不均匀处产生的阴影区域，且细节信息更为丰富。
图 3 2种大气散射模型的复原效果对比Figure 3. Comparison of restoration effects of two atmospheric scattering models2.2 双光幕边界约束下的大气光幕估计
考虑到大气光幕中同时含有待估计参数透射率与大气光，因此，本文算法根据式(3)中大气散射模型对大气光幕不等关系的定义，设定上下边界对其进行约束，以求取较为准确的大气光幕。
2.2.1 大气光幕上边界
根据式(3)可以看出，大气光幕总是小于或等于有雾图像的最小通道且大于0，因此，选定雾图的最小通道$ {{\boldsymbol{W}}}(x,y) $为大气光幕的上边界。此外，随着场景深度的叠加，雾浓度升高，视觉可见度会降低，使得图像在远景区域的纹理信息不可见。为了使得所求大气光幕更能准确地表示雾浓度分布的情况，本文对有雾图像的上边界，即最小通道图采用引导滤波[17]处理，以消除纹理与部分无用边缘信息使其更为平滑，以逼近更为真实的大气光幕。
{\boldsymbol{V}}_{1}(x,y)=F_{\mathrm{guide}}{{\boldsymbol{W}}}(x,y)) (10) 式中：$ {\boldsymbol{V}}_{1}(x,y) $表示大气光幕上边界；$F_ {\rm{guide}} $表示引导滤波操作。
2.2.2 大气光幕下边界
大气散射模型中大气光幕$ {{\boldsymbol{V}}}(x,y) $被定义为
{{\boldsymbol{V}}}(x,y) = {{\boldsymbol{A}}}(x,y)[1 - \exp ( - \beta {{\boldsymbol{d}}}(x,y))] (11) 假设大气光$ {{\boldsymbol{A}}}(x,y) $已知，由式（11）中可以看出透射率$ {{\boldsymbol{t}}}(x,y) $与场景深度$ {{\boldsymbol{d}}}(x,y) $呈衰减关系，而大气光幕的大小与透射率或景深的变化有关。因此，本文算法从景深与透射率出发求取大气光幕下边界。
根据文献[6]中的颜色衰减先验可知，随着场景深度的叠加，亮度升高，饱和度降低；即景深$ {{\boldsymbol{d}}}(x,y) $与亮度$ {{\boldsymbol{v}}}(x,y) $呈递增关系，与饱和度$ {{\boldsymbol{s}}}(x,y) $呈衰减关系。引入亮度和饱和度的定义式为
\left\{ \begin{aligned} & {{{\boldsymbol{v}}}(x,y) = \max [{{{\boldsymbol{I}}}^c}(x,y)]} \\ & {{{\boldsymbol{s}}}(x,y) = 1 - [\min [{{{\boldsymbol{I}}}^c}(x,y)]/\max [{{{\boldsymbol{I}}}^c}(x,y)]]} \end{aligned} \right. (12) 对饱和度进行反转，得到反饱和度$ {{{\boldsymbol{s}}}'}(x,y) $为
{{{\boldsymbol{s}}}'}(x,y) = 1 - {{\boldsymbol{s}}}(x,y) = \min [{{{\boldsymbol{I}}}^c}(x,y)]/\max [{{{\boldsymbol{I}}}^c}(x,y)] (13) 根据式(12)和式(13)可以看出饱和度与反饱和度呈衰减关系，结合景深与饱和度呈衰减关系，可以得出景深与反饱和度呈递增关系。
结合透射率$ {{\boldsymbol{t}}}(x,y) $与场景深度$ {{\boldsymbol{d}}}(x,y) $呈衰减关系，场景深度$ {{\boldsymbol{d}}}(x,y) $与亮度$ {{\boldsymbol{v}}}(x,y) $、反饱和度$ {{{\boldsymbol{s}}}'}(x,y) $呈递增关系，可得出透射率$ {{\boldsymbol{t}}}(x,y) $与亮度$ {{\boldsymbol{v}}}(x,y) $、反饱和度$ {{{\boldsymbol{s}}}'}(x,y) $呈衰减关系。本文通过设定衰减因子$ p $来表示这种衰减关系。
\left\{ \begin{aligned} & {{{{\boldsymbol{t}}}_1}(x,y) = {p_{\text{1}}} \cdot [{{\boldsymbol{v}}}(x,y)]} \\ &{{{{\boldsymbol{t}}}_2}(x,y) = {p_{\text{2}}} \cdot [{{{\boldsymbol{s}}}'}(x,y)]} \end{aligned} \right. (14) 以景深分布较为均匀的雾图为例，分析其亮度、饱和度、反饱和度的特征分布及其灰度性能曲线，如图4所示。根据图4(e)的亮度、饱和度、反饱和度随场景深度变化的灰度分布形式可以看出，随着场景深度的叠加，当亮度递增时，饱和度降低，反饱和度增高，进一步印证了本文假设的可行性。
鉴于高斯函数具有较好的衰减特性，本文设定一种均值为1，标准差为$ \sigma $，且幅值进行归一化处理后的高斯衰减函数来拟合前述的衰减关系，由此得到式(14)的近似估计为
\left\{ \begin{aligned} &{{{{\boldsymbol{t}}}_1}(x,y) = \exp \left. {\left\{ { - {{[1 - {{\boldsymbol{v}}}(x,y)]}^2}} \right./{\sigma _1}^2} \right\}} \\ &{{{{\boldsymbol{t}}}_2}(x,y) = \exp \left. {\left\{ { - {{[1 - {{{\boldsymbol{s}}}'}(x,y)]}^2}} \right./{\sigma _2}^2} \right\}} \end{aligned} \right. (15) 考虑到有雾图像在远景处亮度值与反饱和度值偏高；而在近景处则出现亮度值与反饱和值偏低的现象。根据上述分析，场景深度与亮度和反饱和度呈递增关系，将二者进行乘积，场景深度与亮度和反饱和度的乘积形式亦满足递增关系，即
{{\boldsymbol{d}}}(x,y) \propto {{\boldsymbol{v}}}(x,y) \propto {{{\boldsymbol{s}}}'}(x,y) \propto {{\boldsymbol{v}}}(x,y) \cdot {{{\boldsymbol{s}}}'}(x,y) (16) 联合式(12)和式(13)，可得出景深与雾图的最大、最小通道均呈递增关系为
{{\boldsymbol{d}}}(x,y) \propto \max [{{{\boldsymbol{I}}}^c}(x,y)] \propto \min [{{{\boldsymbol{I}}}^c}(x,y)] (17) 结合所得这一结论，本文以有雾图像的灰度均值$ {\text{mean}}[{{{\boldsymbol{I}}}^c}(x,y)] $为阈值将图像划分为远景和近景区域，并设定$ a $和$ {b} $分别作为2个区域的特征值，其中$ a, b \in(0,1) $。$ a $和$ b $可表示为
\left\{ \begin{aligned} & {a = \frac{{\max [{{{\boldsymbol{I}}}^c}(x,y)] - {\text{mean}}[{{{\boldsymbol{I}}}^c}(x,y)]}}{2}} \\ & {b = \frac{{{\text{mean}}[{{{\boldsymbol{I}}}^c}(x,y)] - \min [{{{\boldsymbol{I}}}^c}(x,y)]}}{2}} \end{aligned} \right. (18) 获取特征值后，本文引入均值不等关系对式(15)所估计的透射率进行逼近，这样可以使算法在不涉及大规模优化迭代计算的前提下，最大程度上求取标准差区域内的最优解，使得算法具有自适应的功能。首先，根据数学均值不等关系有
\frac{{2ab}}{{a + b}} \leqslant \sqrt {ab} \leqslant \frac{{a + b}}{2} (19) 结合式(15)，对$ \sigma $进行定义：
\left\{\begin{aligned} &{\sigma _1} = \frac{{2ab}}{{a + b}}\\ &{\sigma _2} = \frac{{a + b}}{2} \end{aligned}\right. (20) 假设大气光已知，利用均值不等式可以得到大气光幕下边界的粗略估计$ {\boldsymbol{V}}'(x,y） $为
{\boldsymbol{V}}'(x,y)=\boldsymbol{A}(x,y)[1-\sqrt{{\boldsymbol{t}}_{1}(x,y)\cdot {\boldsymbol{t}}_{2}(x,y)}] (21) 由于所估计的粗略大气光幕是采用边界逼近的方法，可能会损失部分细节信息，为获取更为准确的大气光幕信息，利用梯度约束[18]结合梯度算子求取边缘代价对粗略大气光幕下边界进行补偿：
\begin{split} &\boldsymbol{E}(x,y)={\displaystyle \sum _{x,y}[{\boldsymbol{V}}_{1}(x,y)-{\boldsymbol{V}}'{(x,y）]}^{2}+}\\ &\quad\quad \eta \{\alpha [\partial {\boldsymbol{V}}_{1}(x,y)/\partial x]^{2}+\beta [{\partial {\boldsymbol{V}}_{1}(x,y)/\partial y]^2}\}\end{split} (22) 式中：$ {{\boldsymbol{E}}}(x,y) $为边缘代价；η为惩罚项系数，便于最小化全局的最优代价函数；$ {\boldsymbol{V}}_{1}(x,y)-{\boldsymbol{V}}'(x,y） $表示细化初始大气光幕上边界与粗略大气光幕下边界的纹理信息之差；等式的右项为惩罚项，用于标记图像的边缘信息；$ \alpha $、$ \beta $为边缘系数，本文采用对数压缩处理，使其具有自适应的能力。
\left\{ \begin{aligned} & {\alpha = {{[\partial \ln \left| {\left. {{{{\boldsymbol{V}}}_1}(x,y)} \right|} \right./\partial x + \varepsilon ]}^{ - 1}}} \\ & {\beta = {{[\partial \ln \left| {\left. {{{{\boldsymbol{V}}}_1}(x,y)} \right|} \right./\partial y + \varepsilon ]}^{ - 1}}} \end{aligned} \right. (23) 为了防止分母为0，取$ \varepsilon $=0.1。由此可得到修正后的大气光幕下边界$ {{{\boldsymbol{V}}}_2}(x,y) $的表达式为
{\boldsymbol{V}}_{2}(x,y)={\boldsymbol{V}}'(x,y）+\boldsymbol{E}(x,y) (24) 2.2.3 大气光幕估计
取上下边界之和的均值作为最终大气光幕$ {\boldsymbol{V}}(x, y) $，表达式为
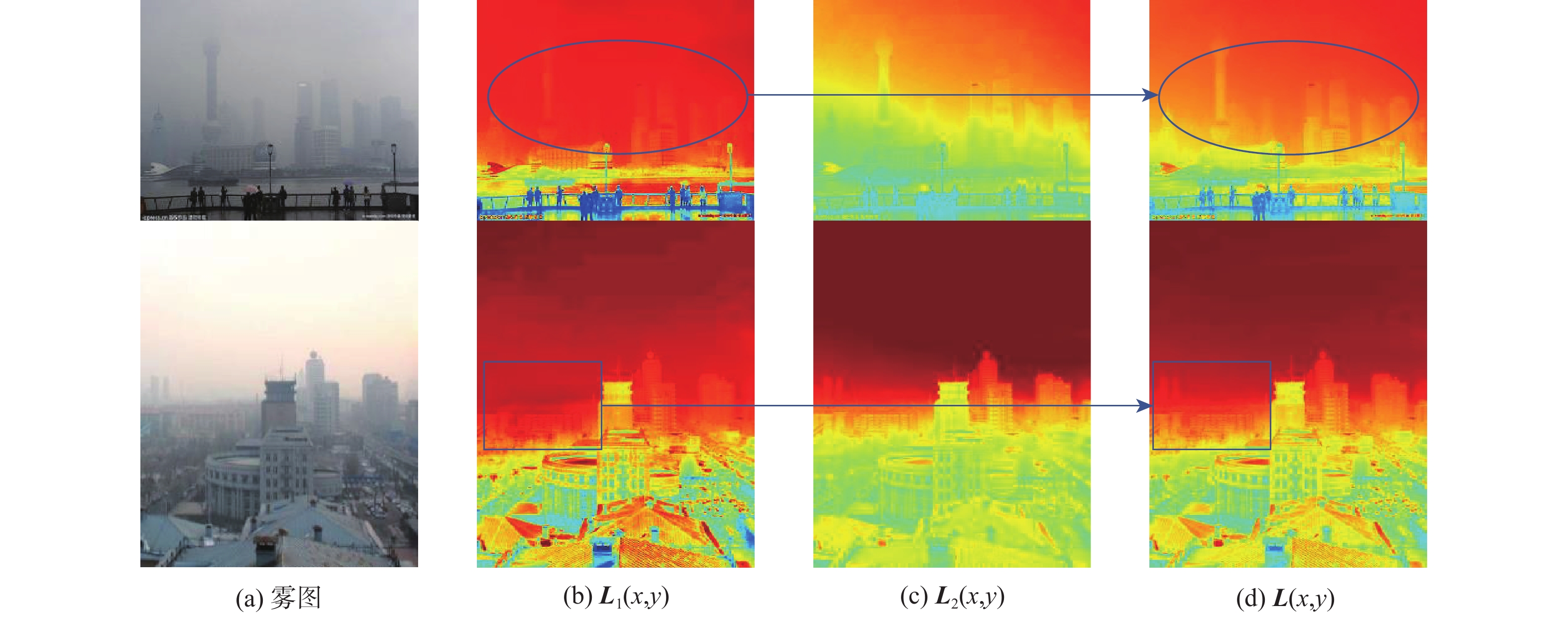
{{\boldsymbol{V}}}(x,y) = \frac{{{{{\boldsymbol{V}}}_1}(x,y) + {{{\boldsymbol{V}}}_2}(x,y)}}{2} (25) 图5为大气光幕估计和复原结果，可以看出所估计出的大气光幕不仅能表示雾浓度的分布特征，且细节保证良好，复原结果色彩鲜明。
图 5 大气光幕估计和复原结果示意图Figure 5. Schematic diagram of atmospheric light curtain estimation and restoration results2.3 场景入射光估计
根据2.1节分析可知，传统大气散射模型中对大气光的定位是不合理的，并没有考虑到场景反射光、背景折射光等光照因素的影响，从而导致雾图的阴暗区域无法得到很好的复原效果。考虑到Retinex理论具有较强的动态压缩能力，能够以较大程度复原图像阴影区域的细节信息，因此，结合式(8)中的入射光图像$ {{\boldsymbol{L}}}(x,y) $，新原图像$ {{{\boldsymbol{S}}}_{{\text{new}}}}(x,y) $，利用Retinex理论引入场景入射光，并得到其粗略估计$ {\boldsymbol{L}}'(x,y) $，表达式为
{\boldsymbol{L}}'(x,y)=(\boldsymbol{I}(x,y)-\boldsymbol{V}(x,y))\otimes F (26) 式中：$ F $选用标准差为0.5，卷积窗口尺寸$ h $由雾图$ {{\boldsymbol{I}}}(x,y) $中尺寸的最小值$ {m} $决定的高斯函数作为中心环绕函数，$ h $的表达式为
h = {{{\mathrm{floor}}(m/50)}} (27) 式中：$ { {\mathrm{floor}}(\cdot) } $表示向负无穷方向取整。
为避免所得场景入射光在处理光照均匀场景时，对目标场景出现过度增强的影响；同时在处理光照不均匀场景时，为保证所得复原场景的真实性，保留些许光照不均匀区域的阴暗程度，对所求场景入射光进行限制：
{{{\boldsymbol{L}}}_1}(x,y) = \max ({{{\boldsymbol{L}}}'}(x,y),{L_0}) (28) 式中：$ {{\boldsymbol{L}}_1}(x,y) $为经过限制约束处理后的初始场景入射光；$ {{{L}}_0} $为初始场景入射光的下限值（本文中$ {L_0}{\text{ = 0}}{\text{.1}} $）。
由于所求场景入射光是由Retinex理论得来，但基于图像增强的去雾方法并未考虑到图像退化的本质，可能会导致最终复原结果出现颜色失真的现象。因此，为了能基于图像退化的本质得到较好的去雾效果，本文引入亮通道先验[19]对所求场景入射光进行补偿，根据亮通道先验所述，在有雾图像的RGB三通道中至少存在一个通道具有较高的像素值，这说明在部分局部区域内这些像素具有很强的场景光反射能力和较高的亮度。所以，亮通道图可以对雾图中受光照影响产生阴影较少的区域起到很好的修补作用，如图像中的远景区域。使得所求场景入射光能覆盖到雾图的各个区域。通常情况下，亮通道被定义为
{{{\boldsymbol{L}}}_2}(x,y) = \mathop {\max }\limits_{y \in {\varOmega }(x,y)} [\mathop {\max ({{{\boldsymbol{I}}}^c}(x,y)} ] (29) 式中：$ {{{\boldsymbol{L}}}_2}(x,y) $为亮通道值；$ {{\boldsymbol{\varOmega}} } $为一个以$ (x, y) $为中心的局部区域。
将所求粗略场景入射光与有雾图像的亮通道按照一定比例进行融合，从而达到对场景入射光进行补偿的目的，表达式为
{{\boldsymbol{L}}}(x,y) = {\lambda _1} \cdot {{{\boldsymbol{L}}}_1}(x,y) + {\lambda _2} \cdot {{{\boldsymbol{L}}}_2}(x,y) (30) 式中：$ {\lambda _1} $和$ {\lambda _2} $为权重参数。由于$ {{{\boldsymbol{L}}}_2}(x,y) $在一定程度上也反映了场景光照的能力，也可作为场景入射光的一种近似估计，与$ {{{\boldsymbol{L}}}_1}(x,y) $在一定程度上具有相似性。考虑到亮通道图在一定程度上反应了图像的亮度信息，因此，本文利用图像存在的亮度特征，对$ {{{\boldsymbol{L}}}_1}(x,y) $和$ {{{\boldsymbol{L}}}_2}(x,y) $的相似性进行度量，从而求取相关系数。在雾天条件下获得的图像，随着雾浓度升高，图像的亮度值也逐渐增大。本文所得大气光幕可反应雾图的雾浓度分布情况，其灰度均值的大小恰可以反映图像的亮度变化，可以将其作为$ {{{\boldsymbol{L}}}_2}(x,y) $的前缀系数。考虑到$ {{{\boldsymbol{L}}}_1}(x,y) $和$ {{{\boldsymbol{L}}}_2}(x,y) $分别是从图像增强与复原两方面对场景入射光进行估计的，二者具有一定的互补性。因此，将二者进行加权融合后，相关系数可表示为
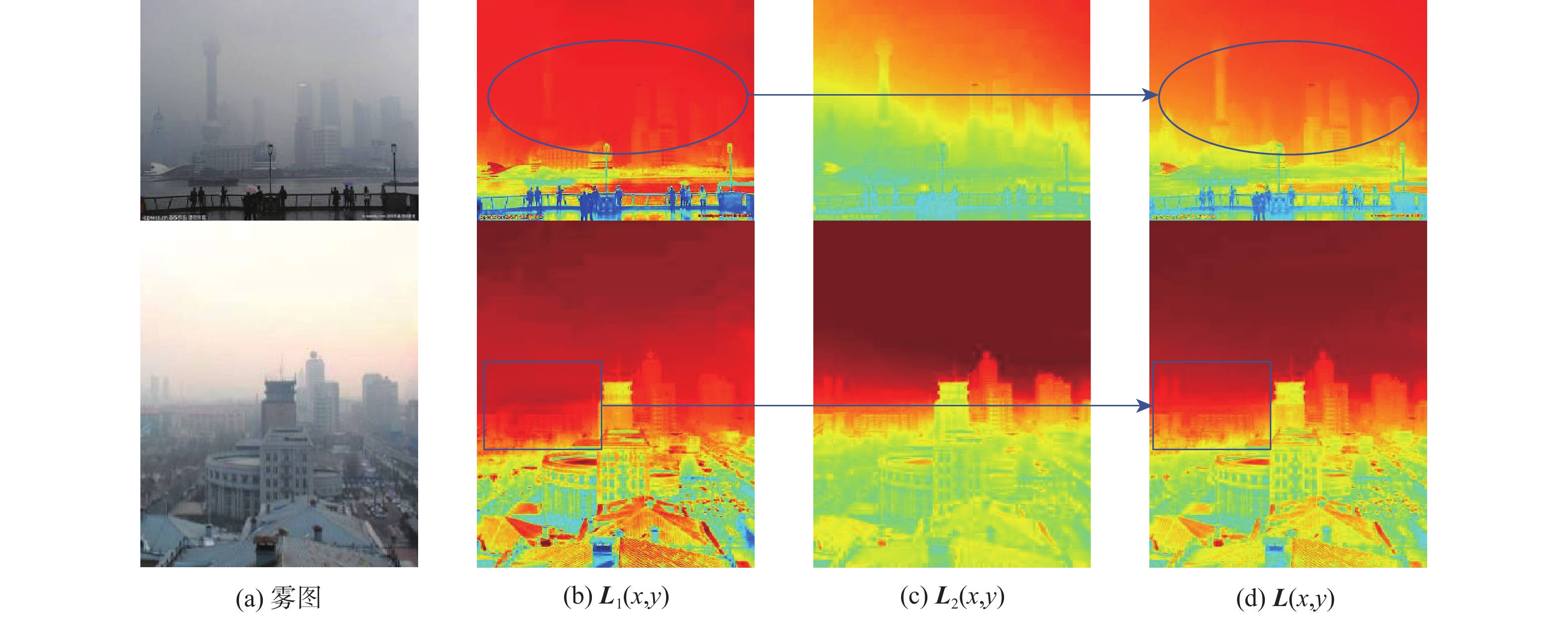
\left\{ \begin{aligned} &{{\lambda _2} = {\text{mean}}[{{\boldsymbol{V}}}(x,y)]} \\ & {{\lambda _1} = 1 - {\lambda _2}} \end{aligned} \right. (31) 本文所求场景入射光如图6所示。根据图中可以看出，虽然亮通道图可以反映图像的整体的光照水平，但并不能将其视为真正的场景入射光。因为场景入射光需要覆盖到图像的各个区域，但亮通道图属于单通道图，无法估算出由于光照不均匀导致反射能力较差处（如阴暗区域）的场景入射光值。但亮通道图作为场景入射光的补偿值是合适的，经过亮通道对粗略场景入射光的补偿后可以看出，补偿后的场景入射光图，不仅对场景的覆盖能力更广，且在一定程度上反应了景深信息，同时避免了由于场景入射光不足导致复原结果颜色失真的问题。
2.4 大气光估计
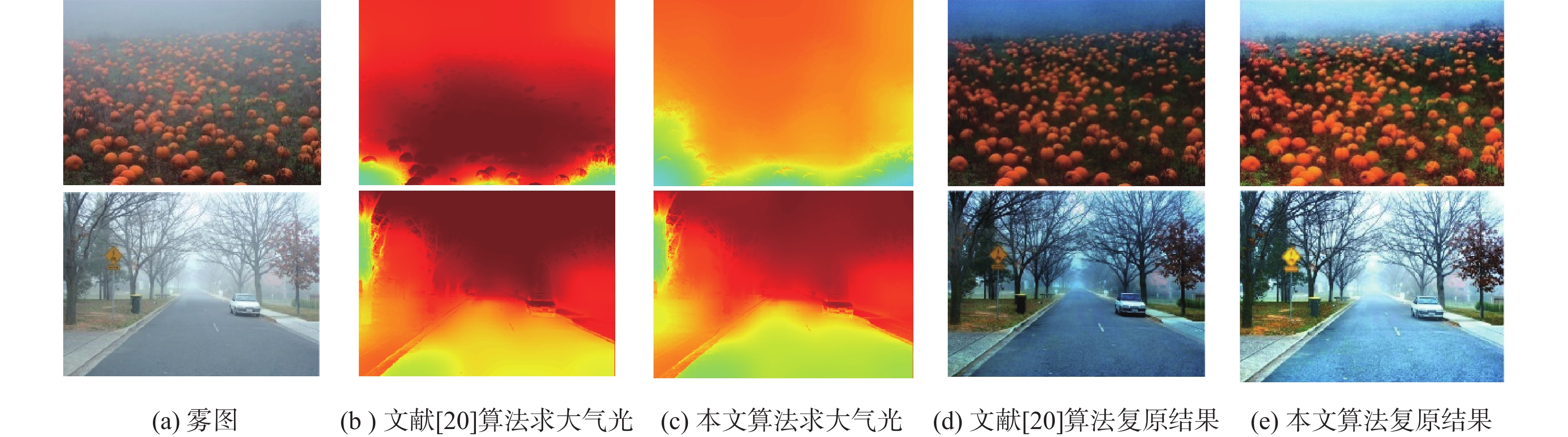
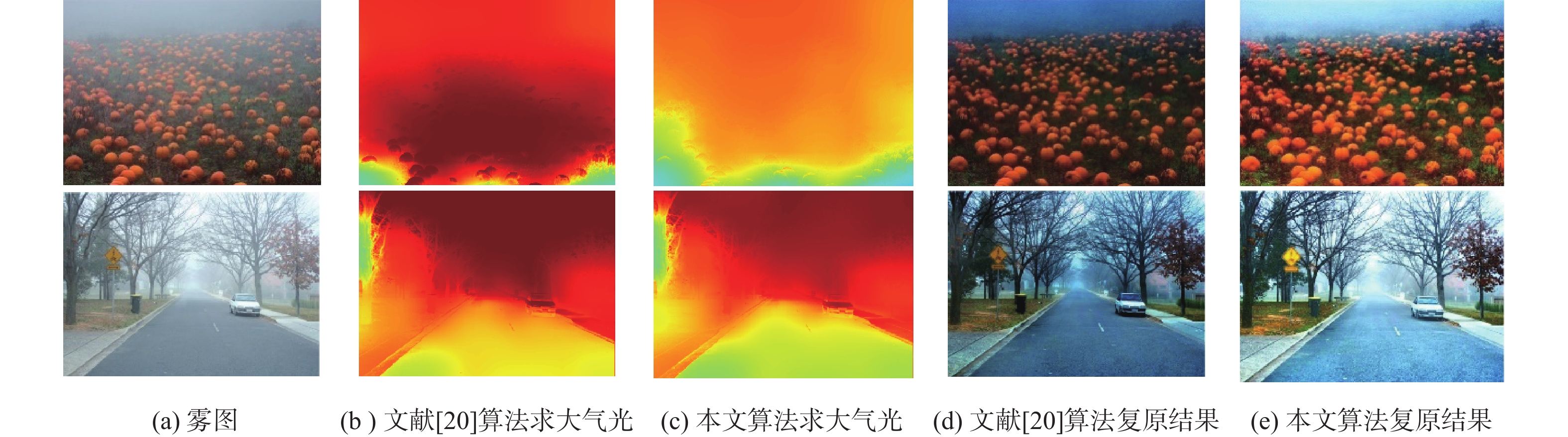
大气光$ {{\boldsymbol{A}}}(x,y) $是去雾问题中另一重要参数，大气光的选取决定了恢复图像的视觉效果。当大气光估计偏高时，结果偏暗；大气光估计偏低时，结果偏亮。文献[20]从图像的局部信息出发，以雾图的三通道最大值为出发点求取大气光，从而减弱了大多数算法从全局信息进行大气光估计带来的影响。但利用三通道最大值会使得大气光的估计偏高，影响复原效果。
为了解决该问题，并减少有雾图像中含有高亮区域对复原结果产生影响，本文提出一种基于中通道的局部大气光求取方法。参照式(19)的均值不等式，将雾图的最大通道和最小通道分别代入不等式的左右两边，可得到有雾图像的中通道表达式为
\left\{ \begin{aligned} & {\max [{{{\boldsymbol{I}}}^c}(x,y)] = \frac{{{a_1} + {b_1}}}{2}} \\ & {\min [{{{\boldsymbol{I}}}^c}(x,y)] = \frac{{2{a_1}{b_1}}}{{{a_1} + {b_1}}}} \end{aligned} \right. \Rightarrow {\text{mid}}[{{{\boldsymbol{I}}}^c}(x,y)] = \sqrt {{a_1}{b_1}} (32) 为避免高亮噪声干扰，对所求中通道进行形态学闭操作，并利用交叉双边滤波对其进行平滑处理，以此得到最终的大气光：
{{\boldsymbol{A}}}(x,y) = F_{\text{BF}}({\mathrm{imclose}}({\text{mid}}[{{{\boldsymbol{I}}}^c}(x,y)],s_{\mathrm{e}})) (33) 式中：$ F_{\mathrm{BF}}(\cdot) $表示交叉双边滤波操作；$ {{\mathrm{imclose}}(\cdot) } $表示形态学闭操作；$s_{\mathrm{e}}$表示结构元素对象。复原效果对比如图7所示。
图 7 大气光图及其复原效果对比Figure 7. Comparison of atmospheric light maps and their restoration effects2.5 图像复原
综合所求大气光幕，场景入射光，大气光，并结合式(7)和式(8)可得到最终的场景反照率为
{{\boldsymbol{\rho}} }(x,y) = \frac{{{{\boldsymbol{A}}}(x,y)[{{\boldsymbol{I}}}(x,y) - {{\boldsymbol{V}}}(x,y)]}}{{{{\boldsymbol{L}}}(x,y)[{{\boldsymbol{A}}}(x,y) - {{\boldsymbol{V}}}(x,y)]}} (34) 最后，将场景反照率限制在[0,1]范围内，可得到无雾图像$ {{\boldsymbol{O}}}(x,y) $，其表达式为
{{\boldsymbol{O}}}(x,y) = \min [\max ({{\boldsymbol{\rho}} }(x,y),0),1] (35) 此外，根据式(9)及其描述，本文引入纹理层图像$ {{\boldsymbol{T}}}(x,y) $改善最终复原效果。考虑到形态学开运算可以对目标图像进行去噪处理，因此，去噪后的图像可近似看作为雾度层图像$ {{\boldsymbol{C}}}(x,y) $，利用有雾图像$ {{\boldsymbol{I}}}(x,y) $减去雾度层图像$ {{\boldsymbol{C}}}(x,y) $即可得到纹理层图像$ {{\boldsymbol{T}}}(x,y) $。具体表达式为
{\boldsymbol{C}}(x,y) = {\mathrm{imopen}}({\boldsymbol{I}}(x,y),s_{\mathrm{e}}) (36) {{\boldsymbol{T}}}(x,y) = {{\boldsymbol{I}}}(x,y) - {{\boldsymbol{C}}}(x,y) (37) 式中：$ { {\mathrm{imopen}}(\cdot) } $表示形态学开运算。因此，最终的雾图复原结果$ {{\boldsymbol{J}}}(x,y) $可表示为
{{\boldsymbol{J}}}(x,y) = {{\boldsymbol{O}}}(x,y) + {{\boldsymbol{T}}}(x,y) (38) 各参量即纹理层添加前后的复原效果对比如图8所示。从图8(c)和图8(d)可以看出，纹理层添加后“飞机机身”较添加前较清晰，添加的前机身有部分灰色杂质，且尾翼处的标志不够清晰，地面处颜色较暗。
图 8 纹理层图像及添加前后复原效果对比Figure 8. Comparison of texture layer images and restoration effects before and after adding算法复原结果及各个未知量估计如图9所示。
3. 实验结果及分析
本文选取了几组不同场景下的真实雾图进行算法验证。并从定性、定量的主客观两方面与一些经典算法进行对比。另外，选取了4幅深度学习算法常用的RESIDE测试集雾图验证对合成图像处理上的可行性。实验环境为MATLAB（R2018a），硬件环境为Intel(R) Core(TM) i7-10510U CPU @ 1.80 GHz，2.30 GHz，运行系统为Windows11。
3.1 去雾质量定性分析
本文选取4组8幅不同场景环境下的真实雾图，分别为光照不均匀图像、颜色变化剧烈图像、远景含天空图像、近景含人物图像。为了验证算法的普适性，在图像复原和深度学习2类方法上，本文各选3种算法进行实验对比，分别与文献[5]算法、文献[6]算法、文献[7]算法、文献[10]算法、文献[12]算法、文献[13]算法的复原结果进行对比。此外，另选取4幅合成雾图与不同算法进行实验对比。
图10为光照不均匀组图像，从图中可以看出文献[5]算法在远景处的复原效果较好，但由于暗通道先验中使用最小滤波操作导致远近景交替处出现光晕效应；文献[6]算法由于透射率估计偏大导致复原结果出现去雾不彻底的问题；文献[7]算法在近景去雾效果较好，在远则存留有稍许残雾，且复原结果整体呈现锐化过度的问题；文献[10]算法出现严重的颜色失真，尤其在近景区域；文献[12]算法与文献[13]算法由于缺乏对真实雾图的训练导致复原结果出现严重的去雾断层现象，特别是文献[13]算法尤为明显。且以上算法在光照不均匀的阴暗区域均无法复原出较为清晰的细节信息，相较于其他算法，本文算法不仅去雾彻底，色彩均衡，且对近景处由于光照不均导致的阴暗区域也能得到较好的复原结果。
图 10 不同算法下光照不均匀图像的复原结果Figure 10. Restoration results of images with uneven light under different algorithms图11为颜色变化剧烈组图像的复原结果，可以看出，文献[5]算法与文献[10]算法此时出现不同程度的颜色失真现象，文献[10]算法的偏色程度相较于文献[5]算法较严重；文献[6]算法与文献[7]算法则出现了不同程度的去雾不彻底现象，文献[6]算法的残雾存留程度相较于文献[7]算法更为严重；文献[12]算法与文献[13]算法同样因为训练不足的原因导致去雾效果不稳定。
图 11 不同算法下颜色变化剧烈图像的复原结果Figure 11. Restoration results of images with drastic color changes under different algorithms图12为远景含天空组图像的复原结果，可以看出文献[5]算法由于对暗通道的估计未考虑到远景天空处，导致透射率严重偏小，使得复原结果的远景天空处出现偏色问题；而文献[6]算法由于是对场景深度进行估计的算法，所以在该组图像中表现较前2组效果较好；文献[7]算法此时在近景区域则出现色失真的问题；文献[10]算法则在远景区域出现了失真的问题；文献[12]算法在该组去雾较为彻底，但色彩偏移较为严重；文献[13]算法则几乎无法去雾。
图 12 不同算法下远景含天空图像的复原结果Figure 12. Restoration results of distant view with sky images under different algorithms图13为近景含人物组图像的复原结果，此时各算法复原效果与图11组图像近景处较为相似。文献[5]算法、文献[7]算法、文献[10]算法、文献[12]算法此时呈现不同程度的颜色失真现象，并伴随些许色彩偏移的问题；文献[6]算法与文献[13]算法则出现去雾不彻底的现象，且该现象在文献[13]算法处理该组图像的人物周围尤其明显。
图 13 不同算法下近景含人物图像的复原结果Figure 13. Restoration results of close shot images with people under different algorithms图14为RESIDE测试集图像的复原结果，可以看出，在处理合成图像时，文献[5]算法、文献[6]算法、文献[7]算法同样出现了上述问题；文献[10]算法、文献[12]算法、文献[13]算法的复原效果较好，更接近真实图像，但文献[12]算法有轻微偏色的问题；而本文算法相较于其他算法，不仅贴合真实图像，且对光照阴影区域也能呈现较好的处理效果。从复原结果与真实场景的对比中可以看出，针对该组图像的第1幅与第4幅图像，图像的阴影区域信息本文算法可以较大程度的对其进行复原。
图 14 不同算法下RESIDE测试集图像的复原结果Figure 14. Restoration results of RESIDE test set images under different algorithms3.2 去雾质量定量分析
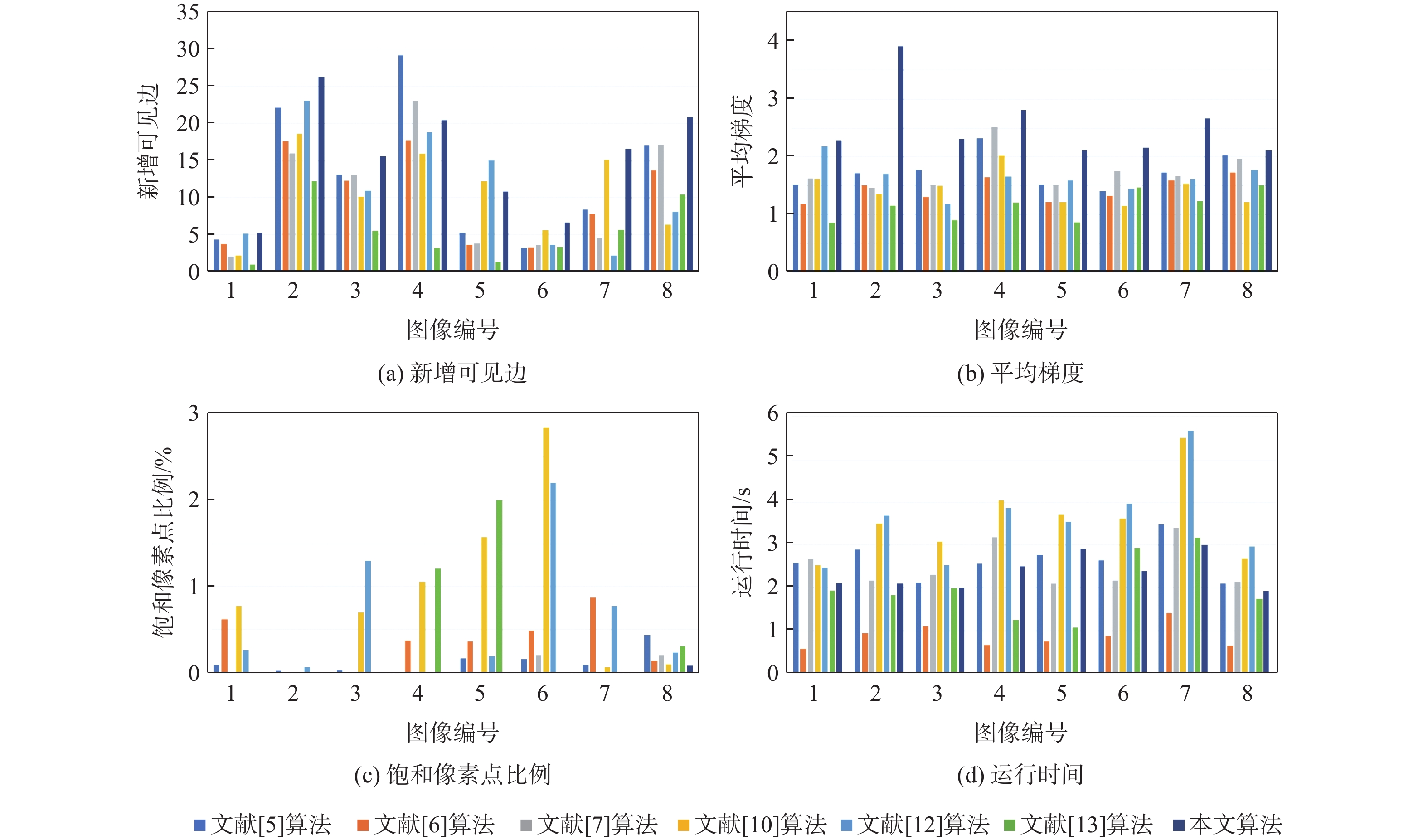
仅依照定性的主观评价的判断较为片面，因此，本文从定量的客观方面进行侧面验证。将新增可见边$ e $、平均梯度$r$、饱和像素点占比$ \delta $及运行时间$ t $作为评价指标[21]。其中，可见边增加率与平均梯度越大代表实验指标效果越好，饱和像素点占比与运行时间越小代表实验指标越好。实验对象为主观评价中所选8幅真实雾图的各算法与本文算法复原结果，各指标的数学形态如式(39)～式(41)所示：
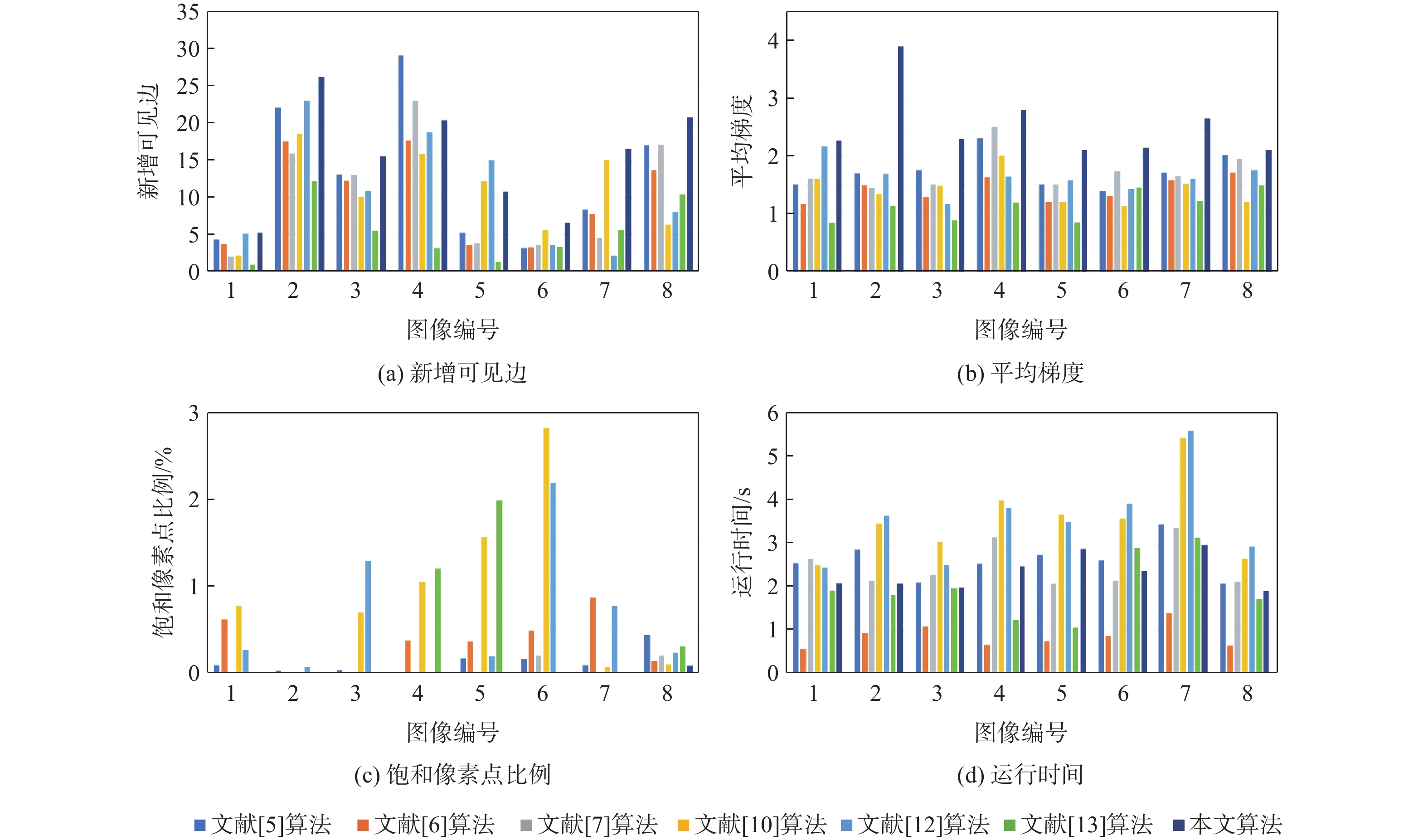
e = \frac{{{n_{\mathrm{r}}} - {n_0}}}{{{n_0}}} (39) r = \exp \left(\frac{1}{{{n_{\mathrm{r}}}}}\sum\limits_{{p_i} \in X} \log_2 {r_i}\right) (40) \delta = \frac{{{n_{\mathrm{s}}}}}{{MN}} (41) 式中：$ n_{{\mathrm{r}}} $和$ n_{0} $分别为算法处理前后雾图和无雾图的可见边数量；$ r_{i} $为$ p_{i} $处去雾前后图像的平均梯度比；$ X $为无雾图像的可见边集合；$ n_{{\mathrm{s}}} $为饱和点像素个数；$ MN $为图像宽与高的尺寸乘积。各算法的定量评价指标如图15所示，图中横轴中色块对应的算法从左至右分别为文献[5]算法、文献[6]算法、文献[7]算法、文献[10]算法、文献[12]算法、文献[13]算法和本文算法。
图 15 各个算法的定量分析指标对比Figure 15. Comparison of quantitative analysis indexes of each algorithms针对测试集图像采用峰值信噪比和结构相似性来测试各算法对合成图像复原效果的优劣程度。两者数值越大表明效果越好。指标对比如表1所示（表中数据为均值）。
表 1 测试集评测指标Table 1. Test set evaluation index通过实验数据指标可以看出，各个算法在客观指标数据下均体现了各自的优势，文献[12]算法在部分图像复原中在新增可见边上存在一定优势；文献[6]算法在运行时间上要优于其他算法；但相较于其他2个指标，本文算法具有一定的优势。在测试集的指标验证方面，本文算法的峰值信噪比优于其他算法，虽然文献[13]算法在结构相似性上取得了较高的指标，但本文算法整体主观效果较好，且优于其他算法。综合以上定性、定量的主客观分析，本文算法具有一定的可行性和应用价值。
4. 结 论
1） 本文算法有效地解决了传统大气散射模型在处理光照不均匀图像时阴暗区域难以复原的问题。
2） 本文算法通过引入场景入射光、细化后的雾图最小通道和亮度、饱和度与透射率的关系结合均值不等关系和特征值估计设定衰减函数等方法，对大气光幕进行估计，并利用亮通道图补偿粗略的场景入射光，并结合中通道理念改进局部大气光。
3） 本文算法可以有效地复原光照不均匀的有雾图像的阴暗区域，并且去雾效果良好，边缘信息保持完整。
-
图 2 大气散射模型物理退化过程
Figure 2. Physical degradation process of atmospheric scattering model
图 3 2种大气散射模型的复原效果对比
Figure 3. Comparison of restoration effects of two atmospheric scattering models
图 5 大气光幕估计和复原结果示意图
Figure 5. Schematic diagram of atmospheric light curtain estimation and restoration results
图 7 大气光图及其复原效果对比
Figure 7. Comparison of atmospheric light maps and their restoration effects
图 8 纹理层图像及添加前后复原效果对比
Figure 8. Comparison of texture layer images and restoration effects before and after adding
图 10 不同算法下光照不均匀图像的复原结果
Figure 10. Restoration results of images with uneven light under different algorithms
图 11 不同算法下颜色变化剧烈图像的复原结果
Figure 11. Restoration results of images with drastic color changes under different algorithms
图 12 不同算法下远景含天空图像的复原结果
Figure 12. Restoration results of distant view with sky images under different algorithms
图 13 不同算法下近景含人物图像的复原结果
Figure 13. Restoration results of close shot images with people under different algorithms
图 14 不同算法下RESIDE测试集图像的复原结果
Figure 14. Restoration results of RESIDE test set images under different algorithms
图 15 各个算法的定量分析指标对比
Figure 15. Comparison of quantitative analysis indexes of each algorithms
-
[1] 蒋华伟, 杨震, 张鑫, 等. 图像去雾算法研究进展[J]. 吉林大学学报(工学版), 2021, 51(4): 1169-1181.JIANG H W, YANG Z, ZHANG X, et al. Research progress of image dehazing algorithms[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(4): 1169-1181 (in Chinese). [2] 江巨浪, 刘国明, 朱柱, 等. 基于快速模糊聚类的动态多直方图均衡化算法[J]. 电子学报, 2022, 50(1): 167-176. doi: 10.12263/DZXB.20201040JIANG J L, LIU G M, ZHU Z, et al. Dynamic multi-histogram equalization based on fast fuzzy clustering[J]. Acta Electronica Sinica, 2022, 50(1): 167-176 (in Chinese). doi: 10.12263/DZXB.20201040 [3] XIAO L M, LI C, WU Z Z, et al. An enhancement method for X-ray image via fuzzy noise removal and homomorphic filtering[J]. Neurocomputing, 2016, 195: 56-64. doi: 10.1016/j.neucom.2015.08.113 [4] LIU H T, LU H Q, ZHANG Y. Image enhancement for outdoor long-range surveillance using IQ-learning multiscale Retinex[J]. IET Image Processing, 2017, 11(9): 786-795. doi: 10.1049/iet-ipr.2016.0972 [5] HE K M, SUN J, TANG X O. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341-2353. doi: 10.1109/TPAMI.2010.168 [6] ZHU Q S, MAI J M, SHAO L. A fast single image haze removal algorithm using color attenuation prior[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2015, 24(11): 3522-3533. doi: 10.1109/TIP.2015.2446191 [7] YANG Y, WANG Z W. Haze removal: Push DCP at the edge[J]. IEEE Signal Processing Letters, 2020, 27: 1405-1409. doi: 10.1109/LSP.2020.3013741 [8] JU M Y, DING C, GUO Y J, et al. IDGCP: Image dehazing based on gamma correction prior[J]. IEEE Transactions on Image Processing, 2020, 29: 3104-3118. doi: 10.1109/TIP.2019.2957852 [9] LI B Y, PENG X L, WANG Z Y, et al. AOD-net: All-in-one dehazing network[C]//Proceedings of the IEEE International Conference on Computer Vision. Piscataway: IEEE Press, 2017: 4780-4788. [10] REN W Q, PAN J S, ZHANG H, et al. Single image dehazing via multi-scale convolutional neural networks with holistic edges[J]. International Journal of Computer Vision, 2020, 128(1): 240-259. doi: 10.1007/s11263-019-01235-8 [11] ZHENG Z R, REN W Q, CAO X C, et al. Ultra-high-definition image dehazing via multi-guided bilateral learning[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2021: 16180-16189. [12] CHEN D D, HE M M, FAN Q N, et al. Gated context aggregation network for image dehazing and deraining[C]//Proceedings of the IEEE Winter Conference on Applications of Computer Vision. Piscataway: IEEE Press, 2019: 1375-1383. [13] BAI H R, PAN J S, XIANG X G, et al. Self-guided image dehazing using progressive feature fusion[J]. IEEE Transactions on Image Processing, 2022, 31: 1217-1229. doi: 10.1109/TIP.2022.3140609 [14] 杨燕, 梁小珍. 基于光幕约束和分段调整的去雾算法[J]. 光子学报, 2021, 50(5): 0510001.YANG Y, LIANG X Z. Dehazing algorithm based on atmospheric veil constraint and piecewise adjustment[J]. Acta Photonica Sinica, 2021, 50(5): 0510001 (in Chinese). [15] NAYAR S K, NARASIMHAN S G. Vision in bad weather[C]// Proceedings of the Seventh IEEE International Conference on Computer Vision. Piscataway: IEEE Press, 1999: 820-827. [16] 杨勇, 邱根莹, 黄淑英, 等. 基于改进大气散射模型的单幅图像去雾方法[J]. 北京航空航天大学学报, 2022, 48(8): 1364-1375.YANG Y, QIU G Y, HUANG S Y, et al. Single image dehazing method based on improved atmospheric scattering model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(8): 1364-1375 (in Chinese). [17] 金仙力, 张威, 刘林峰. 基于引导滤波和自适应容差的图像去雾算法[J]. 通信学报, 2020, 41(5): 27-36. doi: 10.11959/j.issn.1000-436x.2020078JIN X L, ZHANG W, LIU L F. Image defogging algorithm based on guided filtering and adaptive tolerance[J]. Journal on Communications, 2020, 41(5): 27-36 (in Chinese). doi: 10.11959/j.issn.1000-436x.2020078 [18] XIAO C B, ZHAO H Y, YU J, et al. Traffic image defogging method based on WLS[J]. Infrared and Laser Engineering, 2015, 44(3): 1080-1084. [19] MIN X K, ZHAI G T, GU K, et al. Quality evaluation of image dehazing methods using synthetic hazy images[J]. IEEE Transactions on Multimedia, 2019, 21(9): 2319-2333. doi: 10.1109/TMM.2019.2902097 [20] SUN W, WANG H, SUN C H, et al. Fast single image haze removal via local atmospheric light veil estimation[J]. Computers & Electrical Engineering: An International Journal, 2015, 46: 371-383. [21] 韩昊男, 钱锋, 吕建威, 等. 图像去雾方法质量评价[J]. 光学 精密工程, 2022, 30(6): 721-733. doi: 10.37188/OPE.20223006.0721HAN H N, QIAN F, LYU J W, et al. Image dehazing method quality assessment[J]. Optics and Precision Engineering, 2022, 30(6): 721-733 (in Chinese). doi: 10.37188/OPE.20223006.0721 期刊类型引用(0)
其他类型引用(1)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 345
- HTML全文浏览量: 131
- PDF下载量: 25
- 被引次数: 1
