HRG stability period prediction based on signal decomposition and classification modeling
-
摘要:
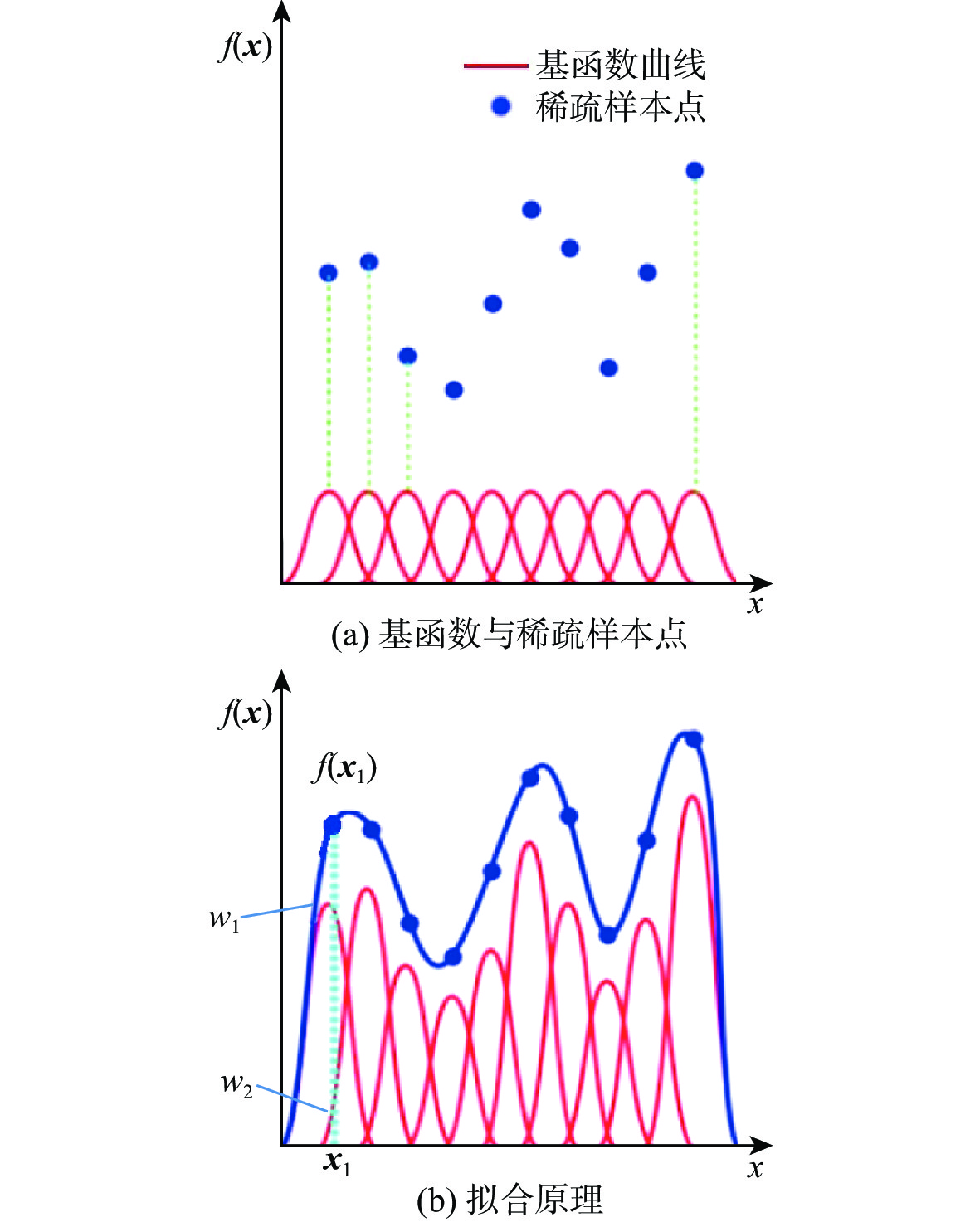
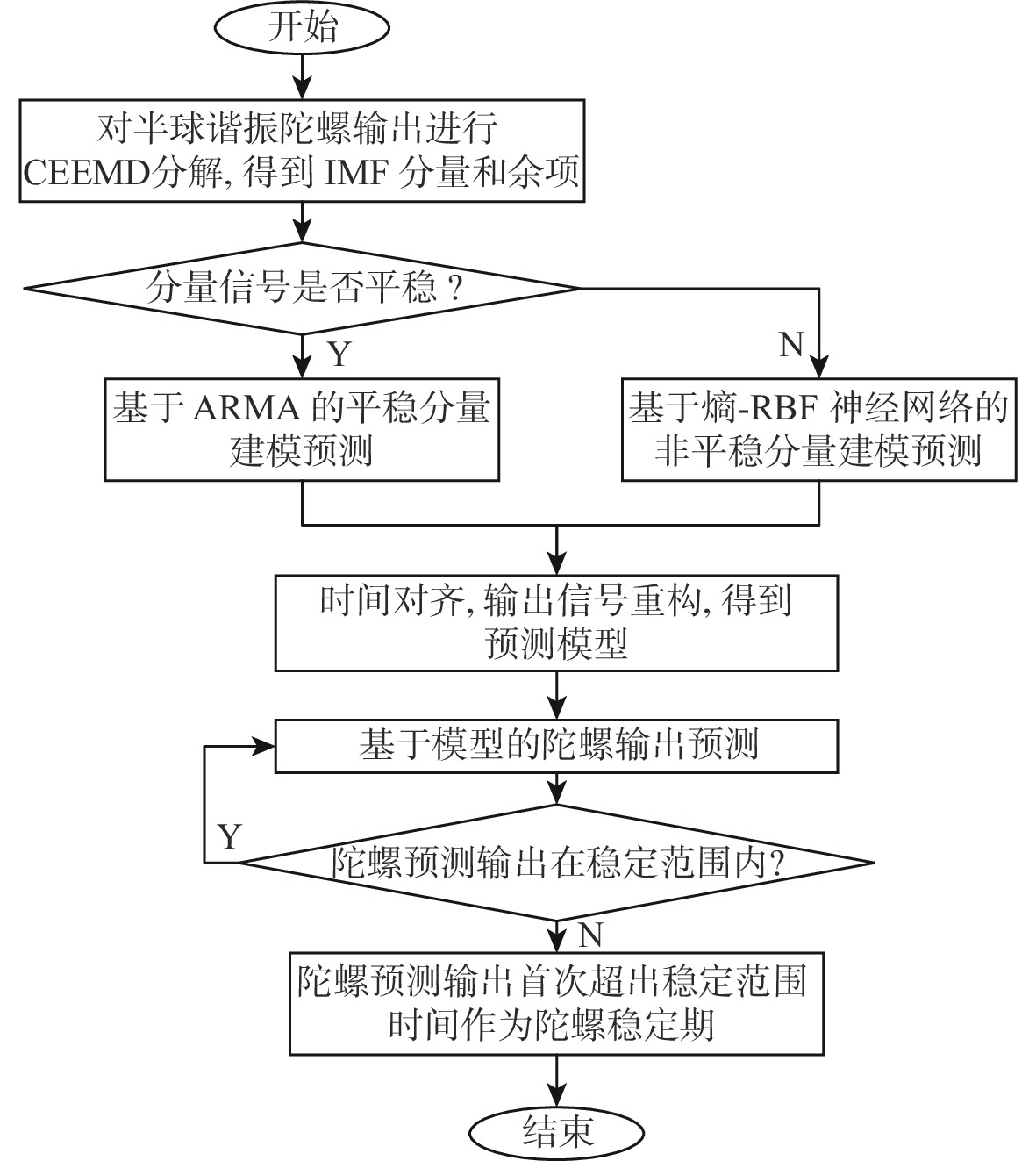
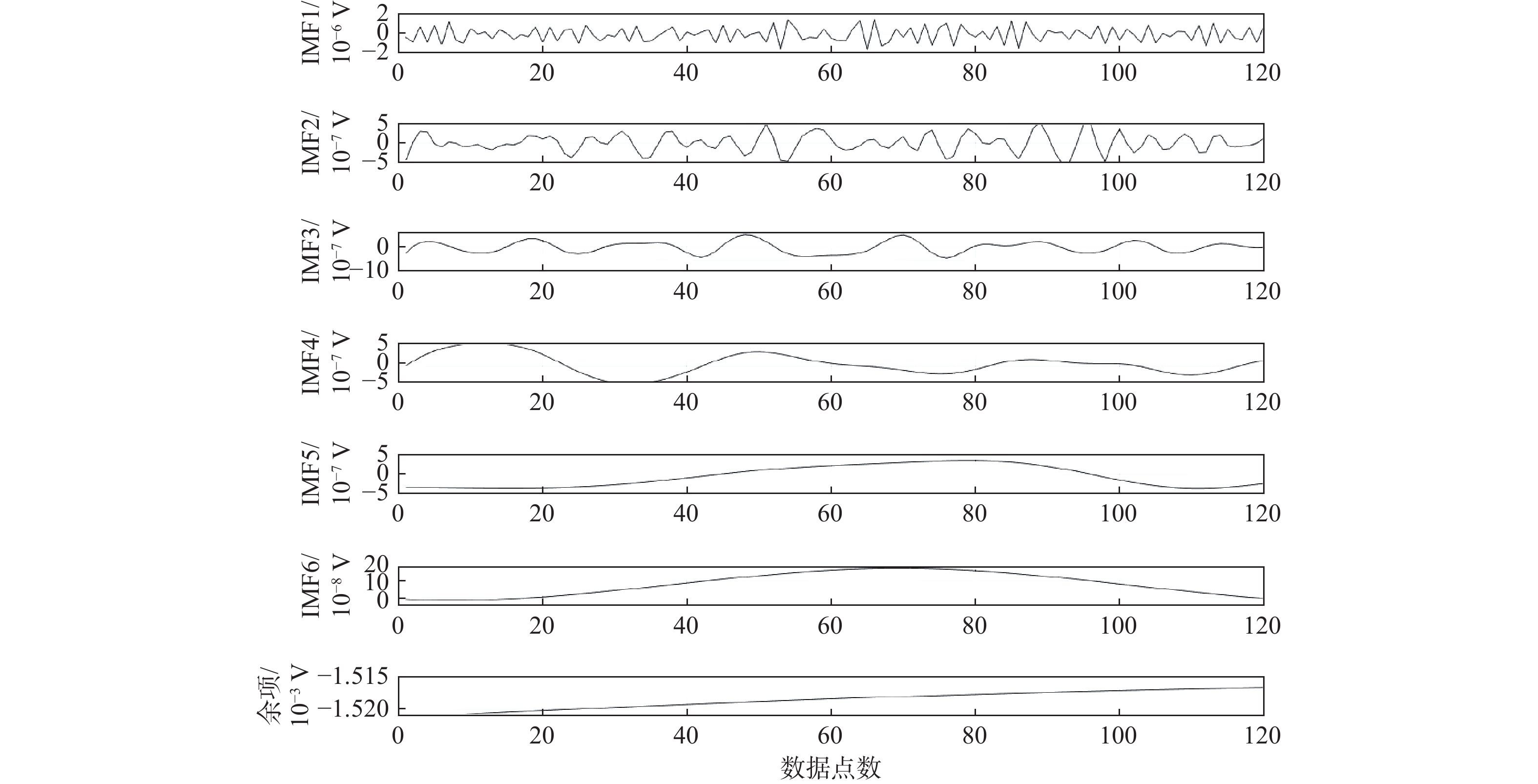
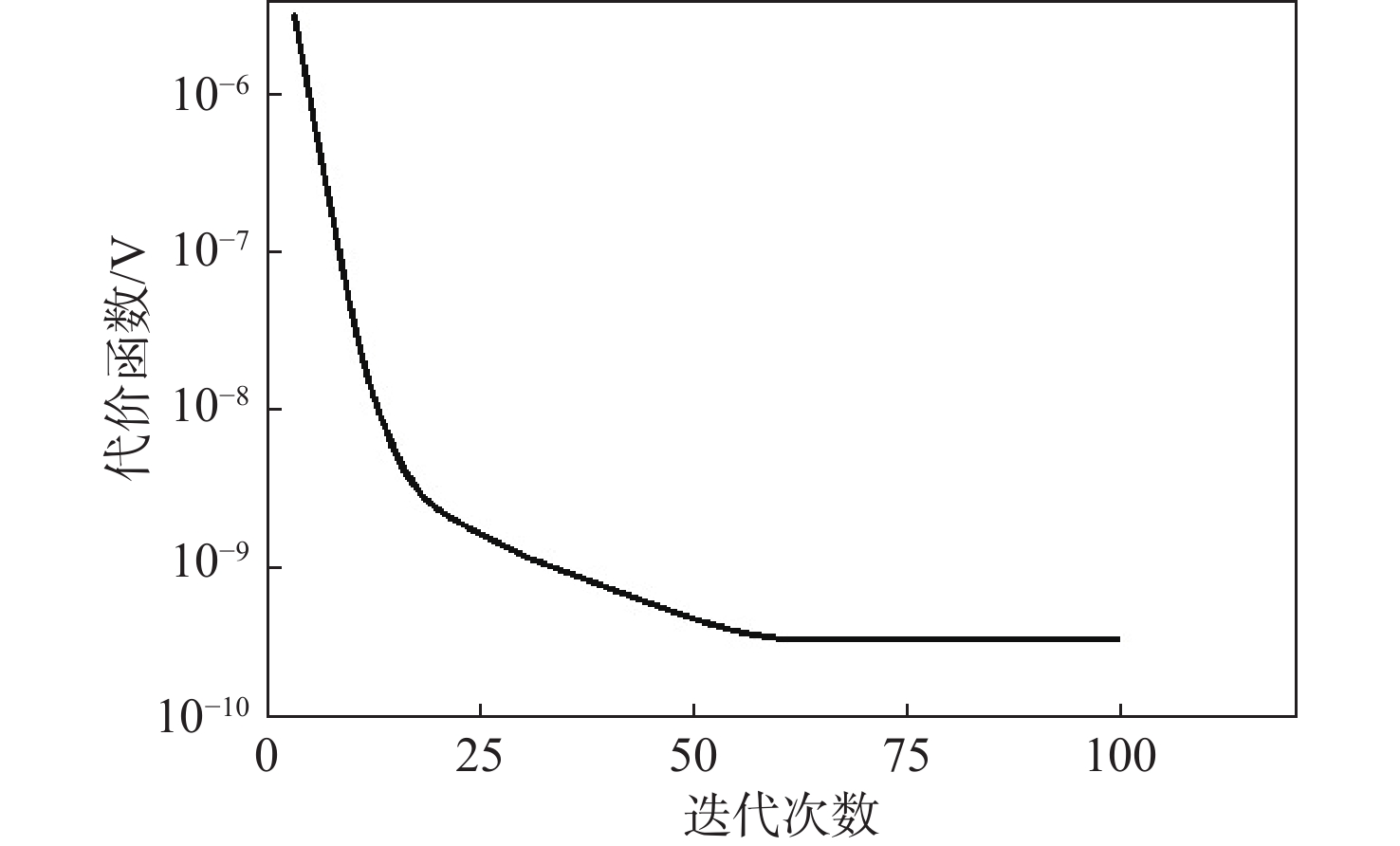
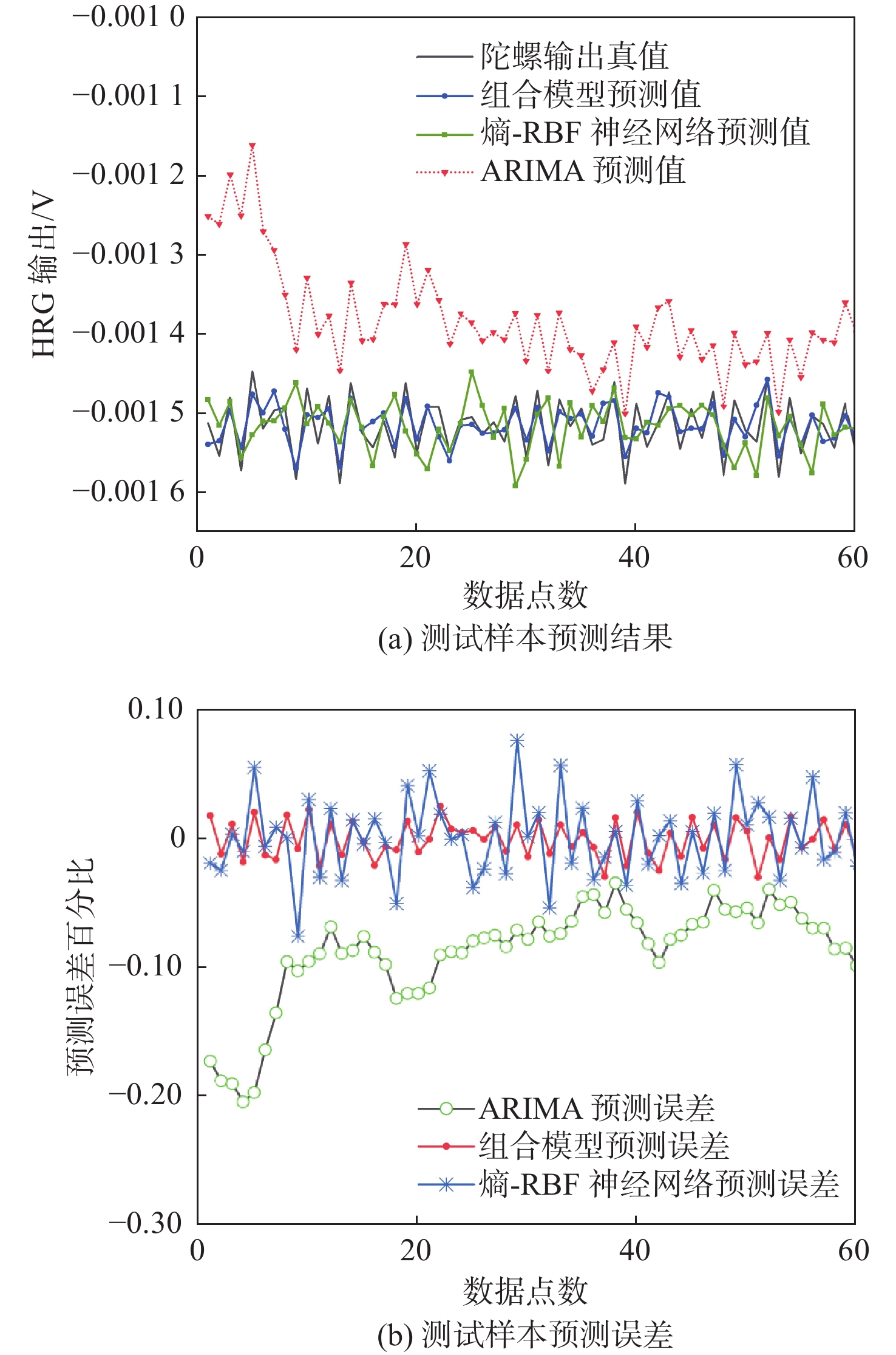
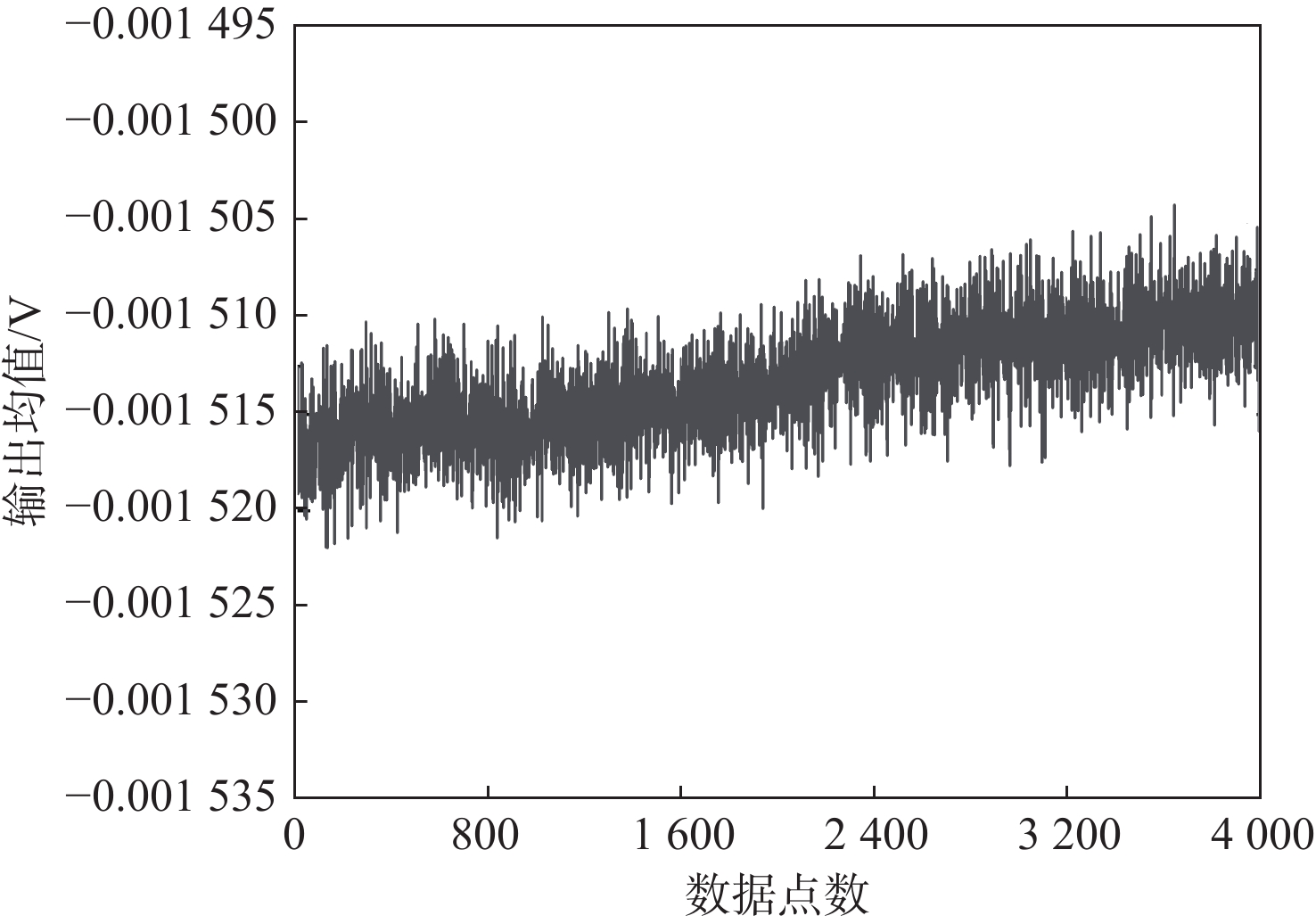
为准确预测半球谐振陀螺(HRG)输出稳定期，提出基于信号分解与分类建模的稳定期预测方法。针对HRG高可靠、长期稳定特点引起的样本变化规律不明显问题，使用具有频率显微镜能力的互补集合经验模态分解(CEEMD)算法对输出进行分解，得到不同频率尺度的信号分量；采用增广Dickey-Fuller(ADF)检验方法对分量信号进行平稳性检验，对于平稳分量建立自回归滑动平均(ARMA)预测模型，对于非平稳分量建立熵-径向基(RBF)神经网络模型。在时间对齐后，分量信号重构得到陀螺输出预测模型。设计陀螺输出稳定标准，给定基于输出预测的稳定期预测流程。经实验验证，组合模型预测平均相对误差仅为1.29%，比自回归积分滑动平均模型(ARIMA)误差减小了1个数量级，比熵-RBF神经网络模型误差减小了约1倍，验证了信号分解与分类建模方法的有效性与高精度。基于陀螺预测输出对陀螺稳定期进行预测，得到了实验陀螺输出稳定期约为3.95年的结论，与实际应用中相一致，说明所提方法的可行性。
-
关键词:
- 半球谐振陀螺 /
- 稳定期预测 /
- 互补集合经验模态分解 /
- 分类建模 /
- 熵-RBF神经网络
Abstract:In order to predict the output stability period of hemispherical resonator gyro (HRG) accurately, a stability period prediction method based on signal decomposition and classification modeling was proposed. The sample variation law is not obvious due to the characteristics of high reliability and long-term stability of HRG. To solve this problem, the complementary ensemble empirical mode decomposition (CEEMD) algorithm with the ability of a frequency microscope was used to decompose the output to obtain the signal components with different frequency scales. The augmented Dickey-Fuller (ADF) method was applied to test the stationarity of component signals. Auto regressive moving average model (ARMA) prediction model was established for stationary components, and the entropy-radial basis function (RBF) neural network model was established for non-stationary components. After time alignment, the component signals were reconstructed to obtain the gyro output prediction model. The gyro output stability standard was designed, and the stability period prediction flow based on output prediction was provided. The experimental results show that the average relative error of the combined model prediction is only 1.29%, which is one order of magnitude less than the error of the autoregressive integrated moving average model (ARIMA) and one time less than the error of the entropy-RBF network model, which verifies the effectiveness and high accuracy of signal decomposition and classification modeling methods. The gyro stability period is predicted based on the gyro prediction output, and the conclusion that the experimental gyro output stability period is 3.95 years is obtained, which is consistent with the practical application, indicating the feasibility of the proposed method.
-
表 1 微机电系统陀螺仪性能指标参数
Table 1. Property index parameters of micro-electro-mechanical system gyro
范围 概率/% $ [\bar x - 1\sigma ,\bar x + 1\sigma ] $ 68.26 $ [\bar x - 2\sigma ,\bar x + 2\sigma ] $ 95.45 $ [\bar x - 3\sigma ,\bar x + 3\sigma ] $ 99.73 
下载: 导出CSV
表 2 分量信号平稳性检验结果
Table 2. Stationarity test results of component signal
信号 统计量 非平稳置信度 原始信号 0.0522 40.651 46 IMF1 −47.590 1 0.001 00 IMF2 −14.178 5 0.001 00 IMF3 −6.597 8 0.001 00 IMF4 −3.579 6 0.001 00 IMF5 −3.061 8 0.002 91 IMF6 0.066 9 0.654 06 余项 12.276 1 0.999 01
下载: 导出CSV
表 3 平稳分量信号建模结果
Table 3. Modeling results of stationary component signal
分量 模型 $ {\alpha }_{1} $ $ {\alpha }_{2} $ $ {\alpha }_{3} $ $ {\beta }_{1} $ $ {\beta }_{2} $ $ {\beta }_{3} $ IMF1 ARMA(2,3) 0 1.7780 1.0060 1.0607 − 0.1690 − 0.6240 IMF2 ARMA(2,3) 0 − 0.7473 0.6739 0.4207 − 0.6800 − 0.4190 IMF3 ARMA(3,3) − 2.1665 1.8724 − 0.5725 1.0526 0.6302 0.3718 IMF4 ARMA(3,3) − 2.7884 2.6795 − 0.8824 1.3629 0.8762 0.2787 IMF5 ARMA(3,3) − 2.9524 2.9194 − 0.9667 1.8700 1.6080 0.6185
下载: 导出CSV
表 4 模型预测误差
Table 4. Prediction error of models
模型 均方根误差/V 平均相对误差/% ARIMA 2.32×10−4 12.56 熵-RBF神经网络 7.91×10−5 2.36 组合模型 2.68×10−5 1.29
下载: 导出CSV
-
[1] 孙一为, 解伟男, 薛智文, 等. 半球谐振陀螺星载惯性测量单元设计与实现[J]. 中国惯性技术学报, 2022, 30(2): 148-153.SUN Y W, XIE W N, XUE Z W, et al. Design and implementation of inertial measurement unit for satellites based on hemispherical resonant gyroscopes[J]. Journal of Chinese Inertial Technology, 2022, 30(2): 148-153(in Chinese). [2] 吴宗收, 汪立新, 李新三, 等. 一种改进PSO-ARMA半球谐振陀螺温度误差建模方法[J]. 北京航空航天大学学报, 2022, 48(6): 1050-1056.WU Z S, WANG L X, LI X S, et al. An improved PSO-ARMA method for temperature error modeling of hemispherical resonator gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(6): 1050-1056(in Chinese). [3] CANDLER R N, HOPCROFT M A, KIM B, et al. Long-term and accelerated life testing of a novel single-wafer vacuum encapsulation for MEMS resonators[J]. Journal of Microelectromechanical Systems, 2006, 15(6): 1446-1456. doi: 10.1109/JMEMS.2006.883586 [4] MA K, SONG N F, JIN J, et al. Radiation-induced degradation analysis and reliability modeling of COTS ADCs for space-borne miniature fiber-optic gyroscopes[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 9505908. [5] 刘吉, 于丽霞, 武锦辉. MEMS陀螺仪加速参数退化的可靠度评估[J]. 探测与控制学报, 2019, 41(6): 33-37.LIU J, YU L X, WU J H. Reliability assessment of MEMS gyro acceleration parameter degradation[J]. Journal of Detection & Control, 2019, 41(6): 33-37(in Chinese). [6] 袁莉芬, 朋张胜, 何怡刚. 基于Copula函数的光纤陀螺贮存可靠性评估[J]. 电子测量与仪器学报, 2020, 34(8): 58-65.YUAN L F, PENG Z S, HE Y G. Evaluating storage reliability of FOG based on Copula function[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(8): 58-65(in Chinese). [7] 秦伟亮, 魏法杰. 基于倒向随机微分方程的光纤陀螺稳定性评估方法[J]. 中国惯性技术学报, 2019, 27(2): 260-265.QIN W L, WEI F J. Evaluation method of FOG stability based on backward stochastic differential equation[J]. Journal of Chinese Inertial Technology, 2019, 27(2): 260-265(in Chinese). [8] YEH J R, SHIEH J S, HUANG N E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. doi: 10.1142/S1793536910000422 [9] 梁言. 基于时间序列平稳性分析的试飞数据稳态段提取[J]. 现代机械, 2020(2): 52-56.LIANG Y. Steady state segment extracting of flight test data based on time series stability analysis[J]. Modern Machinery, 2020(2): 52-56(in Chinese). [10] AKBILGIC O, BOZDOGAN H, BALABAN M E. A novel hybrid RBF neural networks model as a forecaster[J]. Statistics and Computing, 2014, 24(3): 365-375. doi: 10.1007/s11222-013-9375-7 [11] 殷泽凯, 唐家银, 何平. 恒加双应力型相对熵信息融合可靠性评估模型[J]. 机械强度, 2021, 43(4): 841-848.YIN Z K, TANG J Y, HE P. Reliability assessment model based on relative entropy information fusion with double constant accelerating stresses[J]. Journal of Mechanical Strength, 2021, 43(4): 841-848(in Chinese). [12] HAJI S H, ABDULAZEEZ A M. Comparison of optimization techniques based on gradient descent algorithm: A review[J]. PalArch's Journal of Archaeology of Egypt/Egyptology, 2021, 18(4): 2715-2743. [13] 魏传华, 王韶郡, 苏宇楠. 空间变系数地理加权自回归模型的局部GMM估计[J]. 统计与信息论坛, 2022, 37(11): 3-13.WEI C H, WANG S J, SU Y N. Local GMM estimation in spatial varying coefficient geographically weighted autoregressive model[J]. Journal of Statistics and Information, 2022, 37(11): 3-13 (in Chinese). [14] 陈小玲, 张兴发, 李元, 等. 一类带有线性GARCH类误差的滑动平均模型[J]. 数学的实践与认识, 2021, 51(18): 118-131.CHEN X L, ZHANG X F, LI Y, et al. A class of moving average model with linear GARCH type errors[J]. Journal of Mathematics in Practice and Theory, 2021, 51(18): 118-131(in Chinese). [15] SINGH R K, RANI M, BHAGAVATHULA A S, et al. Prediction of the COVID-19 pandemic for the top 15 affected countries: Advanced autoregressive integrated moving average (ARIMA) model[J]. JMIR Public Health and Surveillance, 2020, 6(2): e19115. doi: 10.2196/19115 [16] 郑欣彤, 边婷婷, 张德强, 等. ARIMA和LSTM方法长时间温度观测数据缺失值插补的比较[J]. 计算机应用, 2022, 42(S1): 130-135.ZHENG X T, BIAN T T, ZHANG D Q, et al. Comparison of ARIMA and LSTM methods for interpolation of missing values of long-time temperature observations[J]. Journal of Computer Applications, 2022, 42(S1): 130-135(in Chinese). [17] SCHAFFER A L, DOBBINS T A, PEARSON S A. Interrupted time series analysis using autoregressive integrated moving average (ARIMA) models: A guide for evaluating large-scale health interventions[J]. BMC Medical Research Methodology, 2021, 21(1): 58. doi: 10.1186/s12874-021-01235-8 [18] QIU B M, WANG J W, LI P H. Full digital control of hemispherical resonator gyro under force-to-rebalance mode[J]. IEEE Sensors Journal, 2015, 15(1): 71-75. doi: 10.1109/JSEN.2014.2339229 -
下载:
点击查看大图
计量
- 文章访问数: 138
- HTML全文浏览量: 89
- PDF下载量: 0
- 被引次数: 0
