TBO模式下基于复杂网络的空中交通复杂性分析

彭娅婷; 温祥西; 吴明功; 杨志伟; 王楠

doi:10.13700/j.bh.1001-5965.2023.0231

TBO模式下基于复杂网络的空中交通复杂性分析

doi: 10.13700/j.bh.1001-5965.2023.0231

彭娅婷^{1, 2},
温祥西^{1, 2},
吴明功^{1, 2, ,},
杨志伟³,
王楠³

1.
空军工程大学空管领航学院，西安 710051
2.
国家空管防相撞技术重点实验室，西安 710051
3.
中国人民解放军 93160部队，北京 100800

基金项目: 国家自然科学基金(71801221)；国家社会科学基金(22XGL001)

详细信息

通讯作者:
E-mail：wuminggong@sohu.com

中图分类号: V355
计量
- 文章访问数: 258
- HTML全文浏览量: 84
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-08
- 录用日期: 2023-06-25
- 网络出版日期: 2023-07-25
- 整期出版日期: 2025-04-30

Complex network-based air traffic complexity analysis in TBO

PENG Yating^{1, 2},
WEN Xiangxi^{1, 2},
WU Minggong^{1, 2
, ,},
YANG Zhiwei³,
WANG Nan³

1.
Air Traffic Control and Navigation College，Air Force Engineering University，Xi’an 710051，China
2.
National Key Laboratory of Air Traffic Collision Prevention，Xi’an 710051，China
3.
Unit 93160 of the People’s Liberation Army of China，Beijing 100800，China

Funds: National Natural Science Foundation of China (71801221); National Social Science Fund of China (22XGL001)

More Information

Corresponding author: E-mail：wuminggong@sohu.com

摘要

摘要:
由于依据统一间隔标准构建的复杂网络未考虑机型运行的差异性，不能满足基于航迹运行(TBO)下空中交通复杂性分析的精细化要求。为解决该问题，提出一种基于复杂网络区分不同机型的空中交通复杂性分析模型。建立不同机型侧向飞行安全间隔模型，构建航空器精准保护区，优化飞行冲突网络中航空器连边的判定依据。飞行冲突判断在考虑航空器航向和速度等信息的基础上，关注航空器的不同性能与状态，使飞行冲突网络能够更加贴近TBO的运行模式。通过实验仿真TBO运行环境，同时利用厦门高崎国际机场雷达数据进行验证。结果表明：所提模型较改进前的飞行冲突网络，能够精细化航空器间的水平安全间隔标准，降低空域的复杂度，减轻管制员工作负荷，提高空域的运行效率，为航空器自主选择最优化航迹提供更大的空间。
- 飞行冲突 /
- 复杂网络 /
- 基于航迹运行 /
- 水平间隔标准 /
- 保护区模型
Abstract:
Since the complex network constructed based on the unified spacing standard does not take into account the differences in aircraft type operation, it cannot meet the refined requirements of air traffic complexity analysis under trajectory based operation (TBO). A complex network-based air traffic complexity analysis model is suggested as a solution to this issue in order to differentiate between various aircraft types. In order to create an aircraft precision protection zone and optimize the foundation for identifying the aircraft related edges in the flight conflict network, a lateral flight safety interval calculation model is first developed for various aircraft types. Based on the information on aircraft heading and speed, the flight conflict judgment focuses on different performances and status of aircraft, so that the flight conflict network can be closer to the operation mode of TBO. The findings demonstrate that the model can improve the operational efficiency of the airspace, decrease the complexity of the airspace, lessen the workload of controllers, improve the horizontal separation criteria between aircraft, and give aircraft more freedom to select the best course on their own than the previous flight conflict network.
- flight conflicts /
- complex networks /
- trajectory based operations /
- horizontal separation criteria /
- protected area model

HTML全文

图 1 航空器运动过程示意图

Figure 1. Schematic diagram of the aircraft movement process

下载: 全尺寸图片幻灯片

图 2 三维速度障碍冲突探测模型

Figure 2. Three-dimensional speed barrier conflict detection model

下载: 全尺寸图片幻灯片

图 3 侧向碰撞风险随初始飞行方向夹角变化

Figure 3. Variation of lateral collision risk with initial flight direction angle

下载: 全尺寸图片幻灯片

图 4 蒙特卡罗仿真

Figure 4. Monte Carlo simulation

下载: 全尺寸图片幻灯片

图 5 网络性能对比

Figure 5. Network performance comparison

下载: 全尺寸图片幻灯片

图 6 网络连边下降率分布

Figure 6. Distribution of network connected edge decline rate

下载: 全尺寸图片幻灯片

图 7 网络节点度值分布的对比

Figure 7. Comparison of the distribution of degree values of network nodes

下载: 全尺寸图片幻灯片

图 8 网络节点点强分布的对比

Figure 8. Comparison of point strength distribution of network nodes

下载: 全尺寸图片幻灯片

图 9 网络整体特性指标对比分析

Figure 9. Comparative analysis of overall network characteristics indicators

下载: 全尺寸图片幻灯片

图 10 不同时刻空中运行态势

Figure 10. Airborne operation situation at different moments

下载: 全尺寸图片幻灯片

表 1 最低安全间隔计算模型所需参数值

Table 1. Required parameter values for the minimum safety interval calculation model

航空器	$ {\lambda _x} $/m	$ {\lambda _y} $/m	$ {\lambda _{\textit{z}}} $/m	$ v $/(m·s⁻¹)	$ \beta $/(°)	$ {\sigma _{{\mathrm{cns}}}} $	$ {\sigma _{\rm{w}}} $	$ {\mu _{\rm{w}}} $	$ {N_{\mathrm{p}}} $
A380	72.8	79.8	24.1	251	20	64.5	10.8	60.3	16
B737-800	39.5	35.8	12.5	230	20	64.5	11.5	60.3	16

下载: 导出CSV

表 2 6个等级航空器间侧向安全间隔标准

Table 2. Standards for lateral safety interval between six classes of aircraft

航空器等级	侧向安全间隔/m
航空器等级	A	B	C	D	E	F
A	2582	3779	3841	3873	3930	4028
B	3779	4836	5229	5445	5580	5643
C	3841	5229	5589	5790	5832	6186
D	3873	5445	5790	5870	5995	6223
E	3930	5580	5832	5995	6103	6252
F	4028	5643	6186	6223	6252	6365

下载: 导出CSV

表 3 不同机型组的最小安全间隔

Table 3. Minimum safety distance for different model groups

航空器机型	最小水平安全间隔/m
航空器机型	A380	B737-800	A320	Cessna172	DA40
A380	6365	6227	6222	4209	4361
B737-800	6227	6025	6017	3884	4032
A320	6222	6017	6006	6161	3875
Cessna172	4209	3884	3875	1571	1713
DA40	4361	4032	4024	1713	1856

下载: 导出CSV

表 4 不同时刻的网络指标值

Table 4. Values of network indicators at different moments

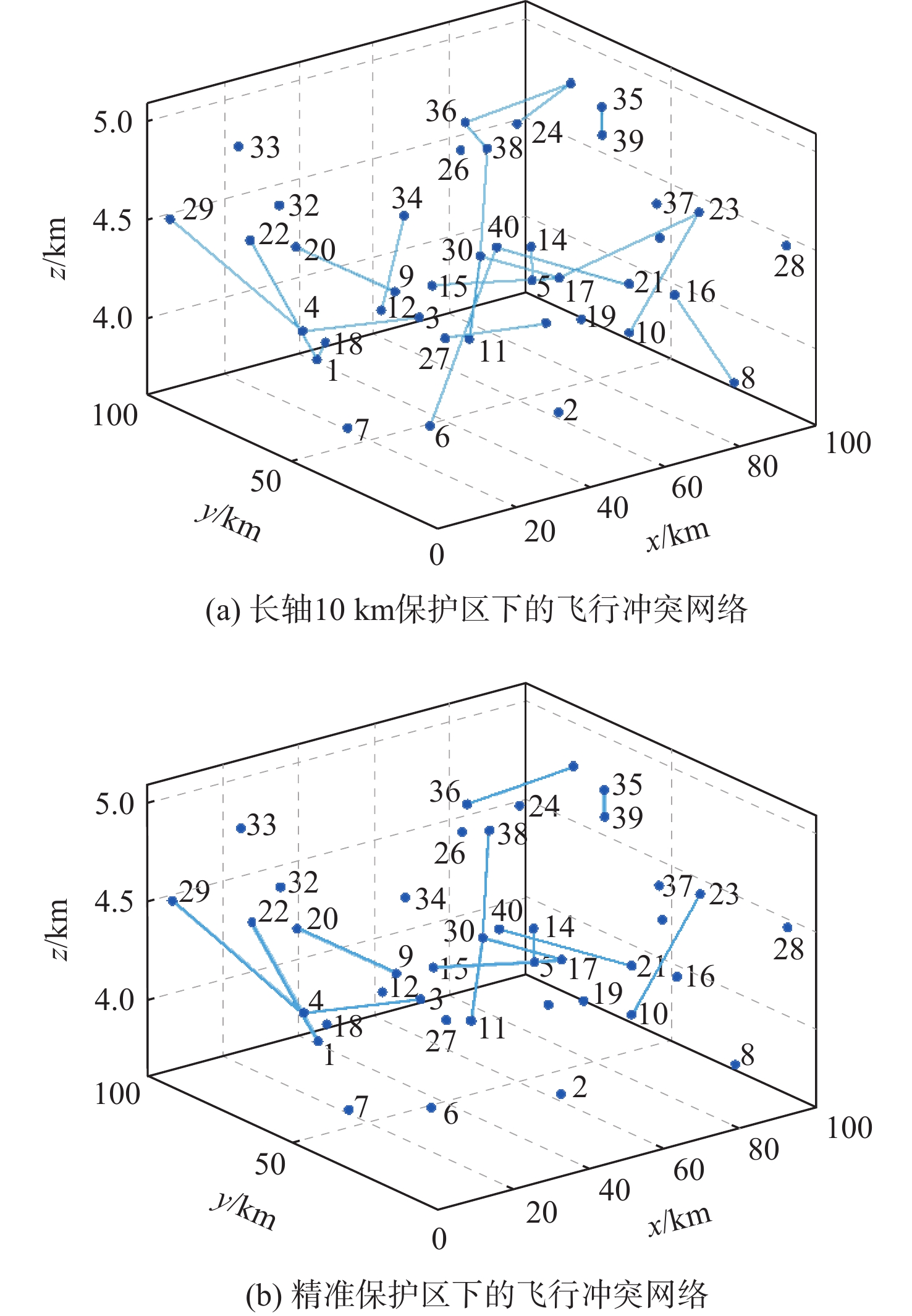
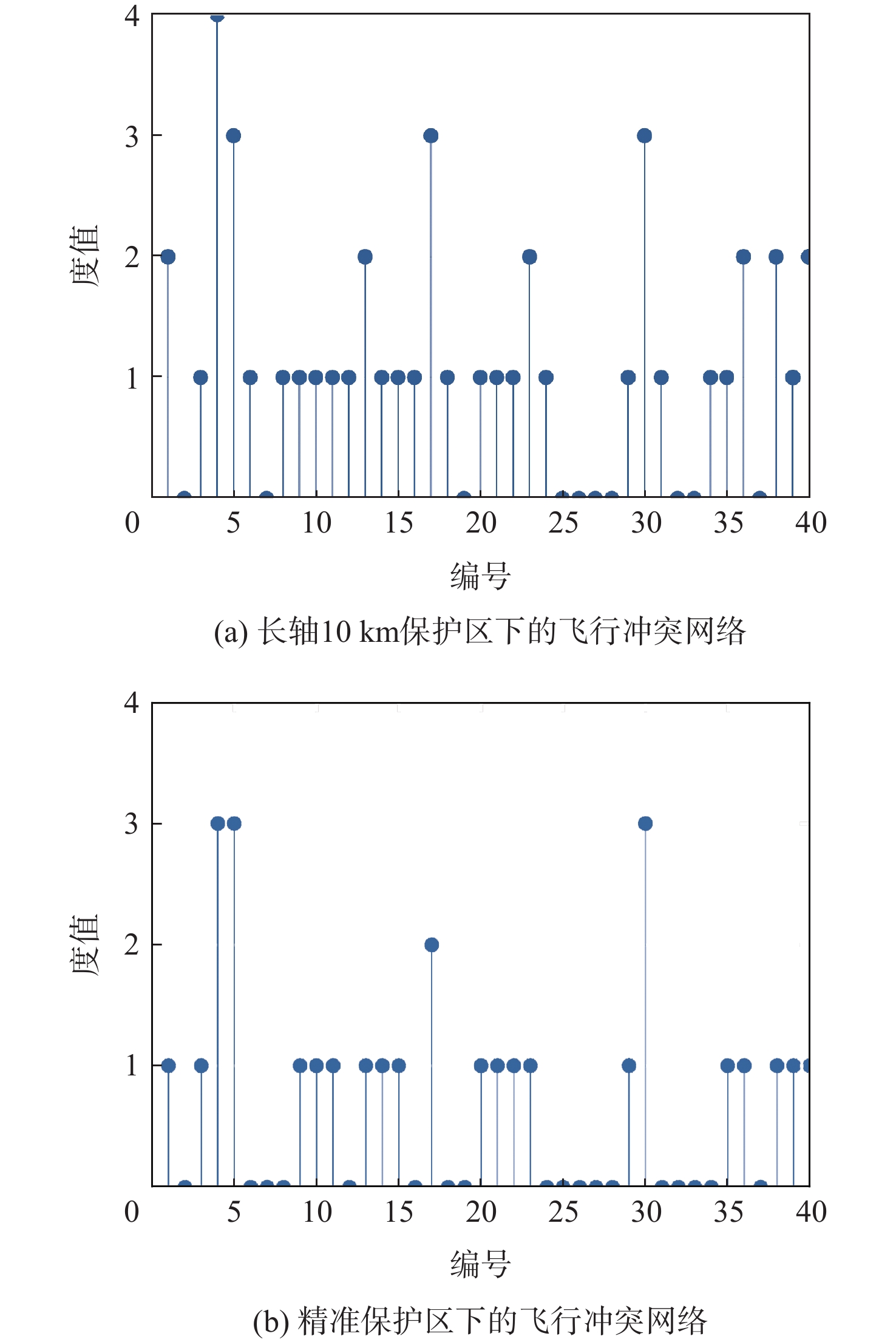
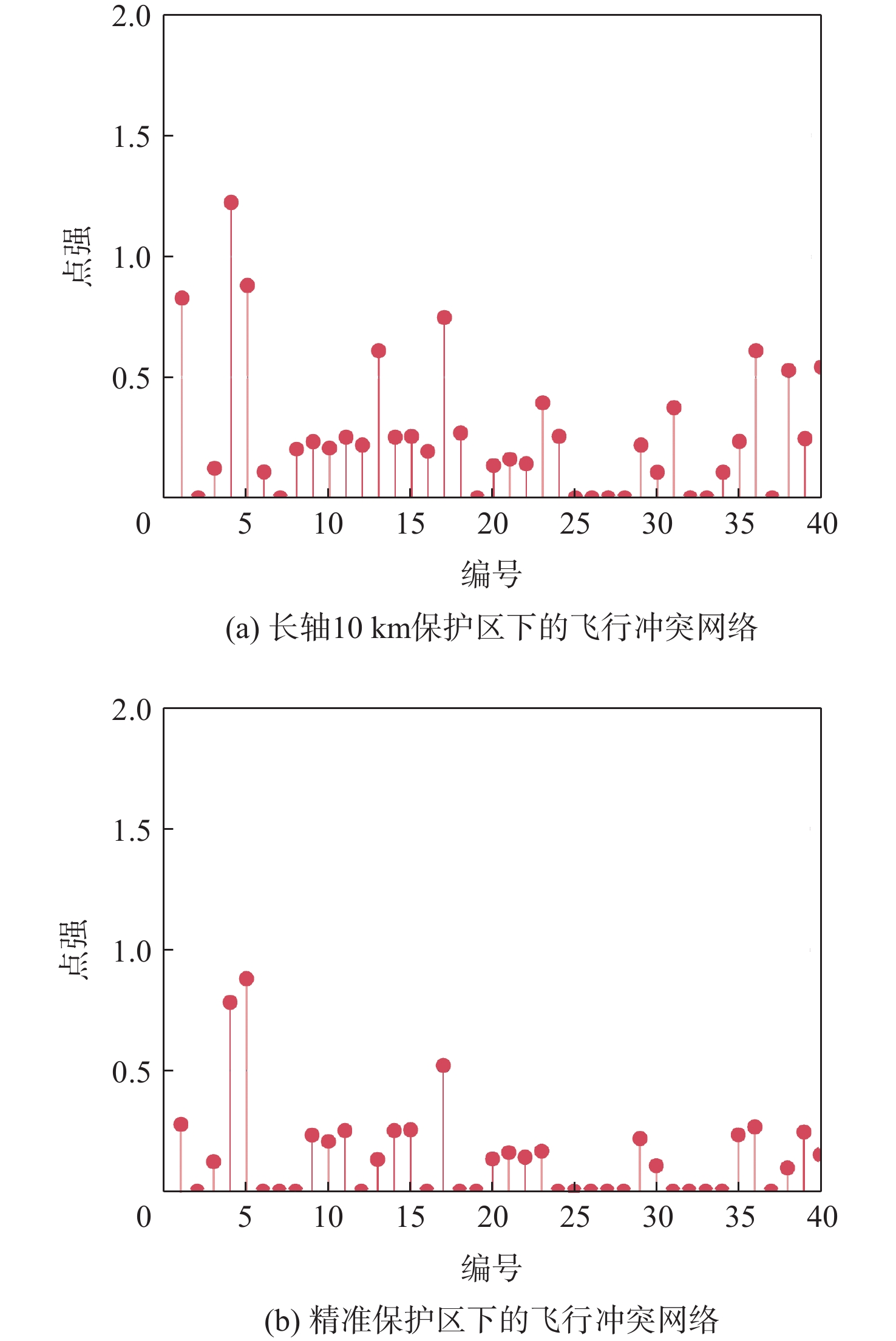
时刻	集聚系数		平均路径长度		网络效率
时刻	长轴10 km保护区下的飞行冲突网络	精准保护区下的飞行冲突网络	长轴10 km保护区下的飞行冲突网络	精准保护区下的飞行冲突网络	长轴10 km保护区下的飞行冲突网络	精准保护区下的飞行冲突网络
12:10	0.4378	0.2686	0.7814	0.2578	1.6449	0.1957
12:20	0.4474	0.2793	0.6832	0.2279	1.7390	0.2189
12:30	0.4665	0.2969	0.5558	0.2360	1.3204	0.2286
12:40	0.4088	0.2329	0.6518	0.1788	1.4386	0.2310

下载: 导出CSV

参考文献(21)

[1]	International Civil Aviation Organization. Global air traffic management operational concept: Doc 9854 AN/458[R]. Montreal: International Civil Aviation Organization, 2005.
[2]	BENTRUP L. Free routing airspace in Europe implementation concepts and benefits for airspace users[J]. International Conference on Research in Air Transportation, 2016: 1-32.
[3]	陈雨童, 胡明华, 杨磊, 等. 受限航路空域自主航迹规划与冲突管理技术[J]. 航空学报, 2020, 41(9): 324045. CHEN Y T, HU M H, YANG L, et al. Autonomous trajectory planning and conflict management technology in restricted airspace[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(9): 324045(in Chinese).
[4]	赵嶷飞, 王梦琦. 空中交通工程学理论内涵与关键科学技术[J]. 航空学报, 2022, 43(12): 026537. ZHAO Y F, WANG M Q. Important theories and critical scientific technology of air traffic engineering[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(12): 026537(in Chinese).
[5]	SCHMIDT D K. On modeling ATC work load and sector capacity[J]. Journal of Aircraft, 1976, 13(7): 531-537. doi: 10.2514/3.44541
[6]	DELAHAYE D, PUECHMOREL S, HANSMAN J, et al. Air traffic complexity map based on non linear dynamical systems[J]. Air Traffic Control Quarterly, 2004, 12(4): 367-388. doi: 10.2514/atcq.12.4.367
[7]	张进, 胡明华, 张晨, 等. 空域复杂性建模[J]. 南京航空航天大学学报, 2010, 42(4): 454-460. doi: 10.3969/j.issn.1005-2615.2010.04.011 ZHANG J, HU M H, ZHANG C, et al. Airspace complexity modeling[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(4): 454-460(in Chinese). doi: 10.3969/j.issn.1005-2615.2010.04.011
[8]	叶博嘉, 胡明华, 张晨, 等. 基于交通结构的空中交通复杂性建模[J]. 交通运输系统工程与信息, 2012, 12(1): 166-172. doi: 10.3969/j.issn.1009-6744.2012.01.025 YE B J, HU M H, ZHANG C, et al. Traffic structure-based air traffic complexity modeling[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(1): 166-172(in Chinese). doi: 10.3969/j.issn.1009-6744.2012.01.025
[9]	王红勇, 赵嶷飞, 温瑞英. 基于复杂网络的空中交通复杂性度量方法[J]. 系统工程, 2014, 32(3): 112-118. WANG H Y, ZHAO Y F, WEN R Y. Air traffic complexity metrics based on complex networks[J]. Systems Engineering, 2014, 32(3): 112-118(in Chinese).
[10]	WANG H Y, WEN R Y, ZHAO Y F. Analysis of topological characteristics in air traffic situation networks[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(13): 2497-2505. doi: 10.1177/0954410015578482
[11]	WANG H Y, SONG Z Q, WEN R Y, et al. Study on evolution characteristics of air traffic situation complexity based on complex network theory[J]. Aerospace Science and Technology, 2016, 58: 518-528. doi: 10.1016/j.ast.2016.09.016
[12]	JIANG X R, WEN X X, WU M G, et al. A complex network analysis approach for identifying air traffic congestion based on independent component analysis[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 523: 364-381. doi: 10.1016/j.physa.2019.01.129
[13]	吴明功, 王泽坤, 甘旭升, 等. 基于复杂网络理论的关键飞行冲突点识别[J]. 西北工业大学学报, 2020, 38(2): 279-287. doi: 10.3969/j.issn.1000-2758.2020.02.007 WU M G, WANG Z K, GAN X S, et al. Identification of key flight conflict nodes based on complex network theory[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 279-287(in Chinese). doi: 10.3969/j.issn.1000-2758.2020.02.007
[14]	吴明功, 叶泽龙, 温祥西, 等. 基于复杂网络的空中交通复杂性识别方法[J]. 北京航空航天大学学报, 2020, 46(5): 839-850. WU M G, YE Z L, WEN X X, et al. Air traffic complexity recognition method based on complex networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(5): 839-850(in Chinese).
[15]	毕可心, 吴明功, 张文斌, 等. 基于速度障碍法的飞行冲突网络建模与分析[J]. 系统工程与电子技术, 2021, 43(8): 2163-2173. doi: 10.12305/j.issn.1001-506X.2021.08.18 BI K X, WU M G, ZHANG W B, et al. Modeling and analysis of flight conflict network based on velocity obstacle method[J]. Systems Engineering and Electronics, 2021, 43(8): 2163-2173(in Chinese). doi: 10.12305/j.issn.1001-506X.2021.08.18
[16]	ERZBERGER H, PAIELLI R, ISAACSON D. Conflict detection and resolution in the presence of prediction error[C]//Proceeding of the 1st USA/Europe Air Traffic Management R&D Seminar. Washington, D.C.: NASA, 1997: 1-15.
[17]	中华人民共和国国务院. 中华人民共和国飞行基本规则[S]. 北京:中华人民共和国国务院,2007. The State Council the People’s Republic of China. Flight basic rules of the People’s Republic of China[S]. Beijing: The State Council the People’s Republic of China, 2007(in Chinese).
[18]	MOEK G, LUTZ E, MOSBERG W. Risk assessment of RNP 10 and RVSM in the south Atlantic flight identification regions: 21401-7465[R]. Annapolis: ARINC, 2001.
[19]	王欣, 徐肖豪. 空中飞机侧向间隔标准的初步研究[J]. 中国民航学院学报(综合版), 2001, 19(1): 1-5. WANG X, XU X H. Study of lateral separation in air traffic control[J]. Journal of Civil Aviation University of China, 2001, 19(1): 1-5(in Chinese).
[20]	张兆宁, 时瑞军. 自由飞行下基于冲突解脱的碰撞风险模型研究[J]. 安全与环境工程, 2016, 23(2): 157-161. ZHANG Z N, SHI R J. Study on free flight collision risk model based on conflict resolution[J]. Safety and Environmental Engineering, 2016, 23(2): 157-161(in Chinese).
[21]	International Givil Aviation Organization. Convention on international civil aviation: Doc T300[S]. Montreal: International Givil Aviation Organization, 2006.