针对高机动目标的深度强化学习智能拦截制导

张豪; 朱建文; 李小平; 包为民

doi:10.13700/j.bh.1001-5965.2023.0375

针对高机动目标的深度强化学习智能拦截制导

doi: 10.13700/j.bh.1001-5965.2023.0375

张豪¹,
朱建文^{1, 2, ,},
李小平¹,
包为民^{1, 3}

1.
西安电子科技大学空间科学与技术学院，西安 710126
2.
火箭军工程大学导弹工程学院，西安 710025
3.
中国航天科技集团有限公司，北京 100048

详细信息

通讯作者:
E-mail：zhujianwen1117@163.com

中图分类号: V448；TJ765.3
计量
- 文章访问数: 453
- HTML全文浏览量: 95
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-15
- 录用日期: 2023-09-11
- 网络出版日期: 2023-09-27
- 整期出版日期: 2025-06-30

Deep reinforcement learning intelligent guidance for intercepting high maneuvering targets

ZHANG Hao¹,
ZHU Jianwen^{1, 2
, ,},
LI Xiaoping¹,
BAO Weimin^{1, 3}

1.
School of Aerospace Science and Technology，Xidian University，Xi’an 710126，China
2.
College of Missile Engineering，Rocket Force University of Engineering，Xi’an 710025，China
3.
China Aerospace Science and Technology Corporation，Beijing 100048，China

More Information

Corresponding author: E-mail：zhujianwen1117@163.com

摘要

摘要:
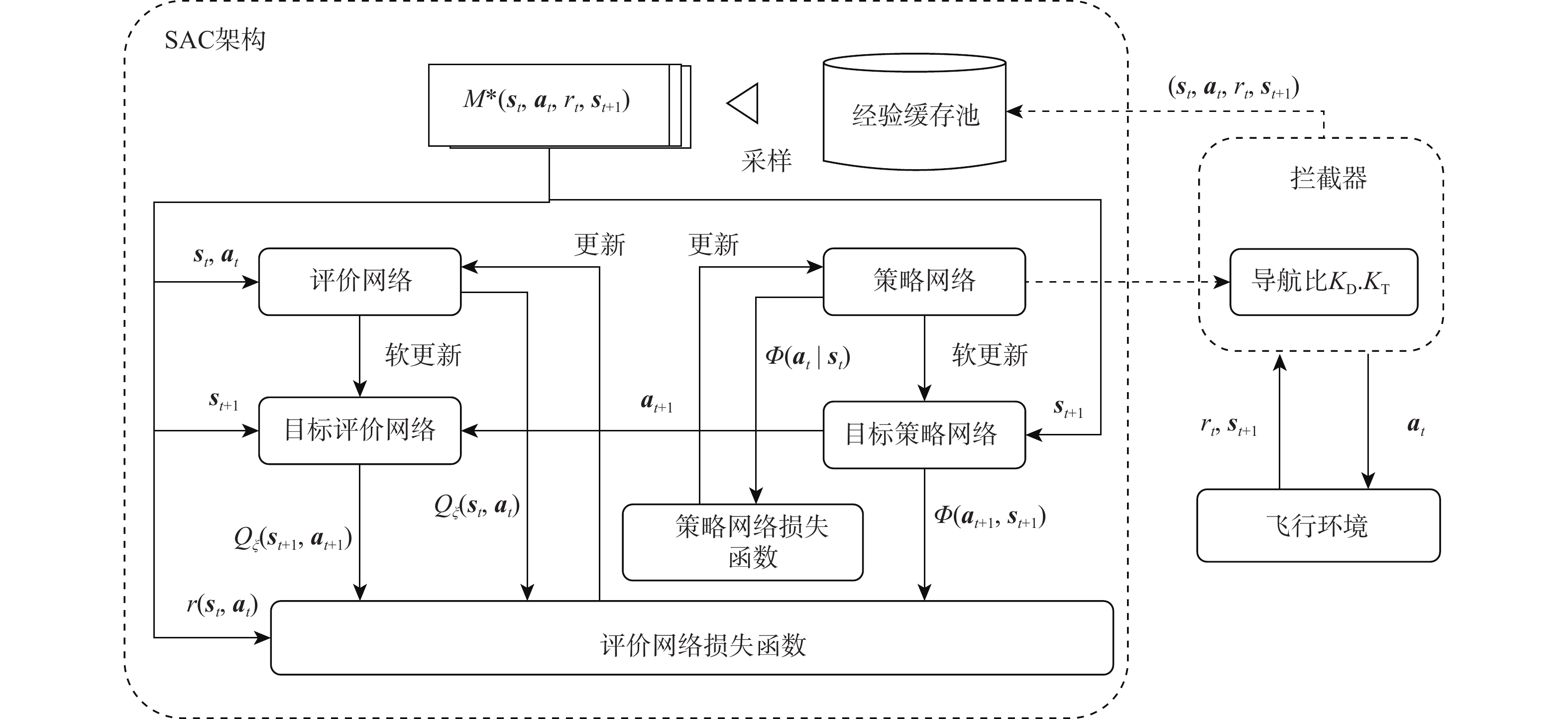
针对固定系数比例导引律在拦截高机动目标时脱靶量与能量损耗过大的问题，提出一种基于深度强化学习智能调参的自适应比例导引律。建立基于实时飞行状态的状态空间和包含横向、纵向导航比的动作空间，以及综合不同状态的奖励函数模型；在奖励函数的模型设计中,引入预测-校正方法，以提高动作评估的准确性；利用柔性演员-评论(SAC)算法，根据拦截器和目标的相对运动状态，训练获得综合考虑脱靶量和能量损耗的网络参数与制导参数决策系统。仿真结果表明：相较于传统比例导引律，所提制导策略可在保证低脱靶量的同时显著降低能量损耗，并且对未训练场景具有良好的适应性。
- 智能制导 /
- 机动目标 /
- 深度强化学习 /
- 比例导引 /
- 马尔可夫决策过程
Abstract:
An adaptive proportional navigation law with intelligent parameter adjustment by deep reinforcement learning is presented to address the issue of excessive miss distances and energy loss in the interception of moving targets using fixed coefficient proportional navigation law. First, a state space based on real-time flight states, an action space containing lateral and vertical gains, and a reward function model integrating different states is established. Meanwhile, a prediction-correction method is introduced to improve the accuracy of action evaluation in the model design of the reward function. Secondly, the soft actor-critic (SAC) algorithm is employed to train a network parameter and guidance parameter decision system that takes into account the miss distances and energy loss according to the relative motion states of the interceptor and the target. In comparison to traditional proportional navigation guidance, the simulation results demonstrate that the guidance technique has strong adaptability and can greatly minimize energy loss while retaining low miss distances.
- intelligent guidance /
- maneuvering targets /
- deep reinforcement learning /
- proportional navigation /
- Markov decision process

HTML全文

图 1 拦截弹-目标相对运动关系

Figure 1. Interceptor-target relative motion relationship

下载: 全尺寸图片幻灯片

图 2 基于SAC的策略训练架构

Figure 2. Strategy training architecture based on SAC

下载: 全尺寸图片幻灯片

图 3 总奖励曲线

Figure 3. Curves of total reward

下载: 全尺寸图片幻灯片

图 4 脱靶量曲线

Figure 4. Curve of miss distance

下载: 全尺寸图片幻灯片

图 5 总过载和曲线

Figure 5. Curve of total overload

下载: 全尺寸图片幻灯片

图 6 温度系数曲线

Figure 6. Curve of temperature coefficient

下载: 全尺寸图片幻灯片

图 7 有无过程奖励下终端奖励曲线

Figure 7. Terminal reward curves with or without process reward

下载: 全尺寸图片幻灯片

图 8 不同制导律下拦截器参数变化曲线

Figure 8. Curves of interceptor parameters with different guidance laws

下载: 全尺寸图片幻灯片

图 9 目标速度曲线

Figure 9. Target speed profile

下载: 全尺寸图片幻灯片

图 10 方波机动下终端参数

Figure 10. Terminal parameters under square wave maneuvering

下载: 全尺寸图片幻灯片

图 11 低过载下终端参数

Figure 11. Terminal parameters under low overload

下载: 全尺寸图片幻灯片

表 1 奖励函数中的权重

Table 1. Weights in the reward function

${k_{{\text{dp}}}}$	${k_{{\text{de}}}}$	${k_{{\text{np}}}}$	${k_{{\text{ne}}}}$	${k_{\text{b}}}$
−0.1	−0.5	−1	−4	100

下载: 导出CSV

表 2 策略网络和评价网络结构

Table 2. Architecture of the policy and critic networks

网络层	节关数
网络层	策略网络	评价网络
输入层	7	9
隐藏层1	256	256
隐藏层 2	256	256
隐藏层3	256	256
输出层	4	1

下载: 导出CSV

表 3 超参数设置

Table 3. Hyperparameters setting

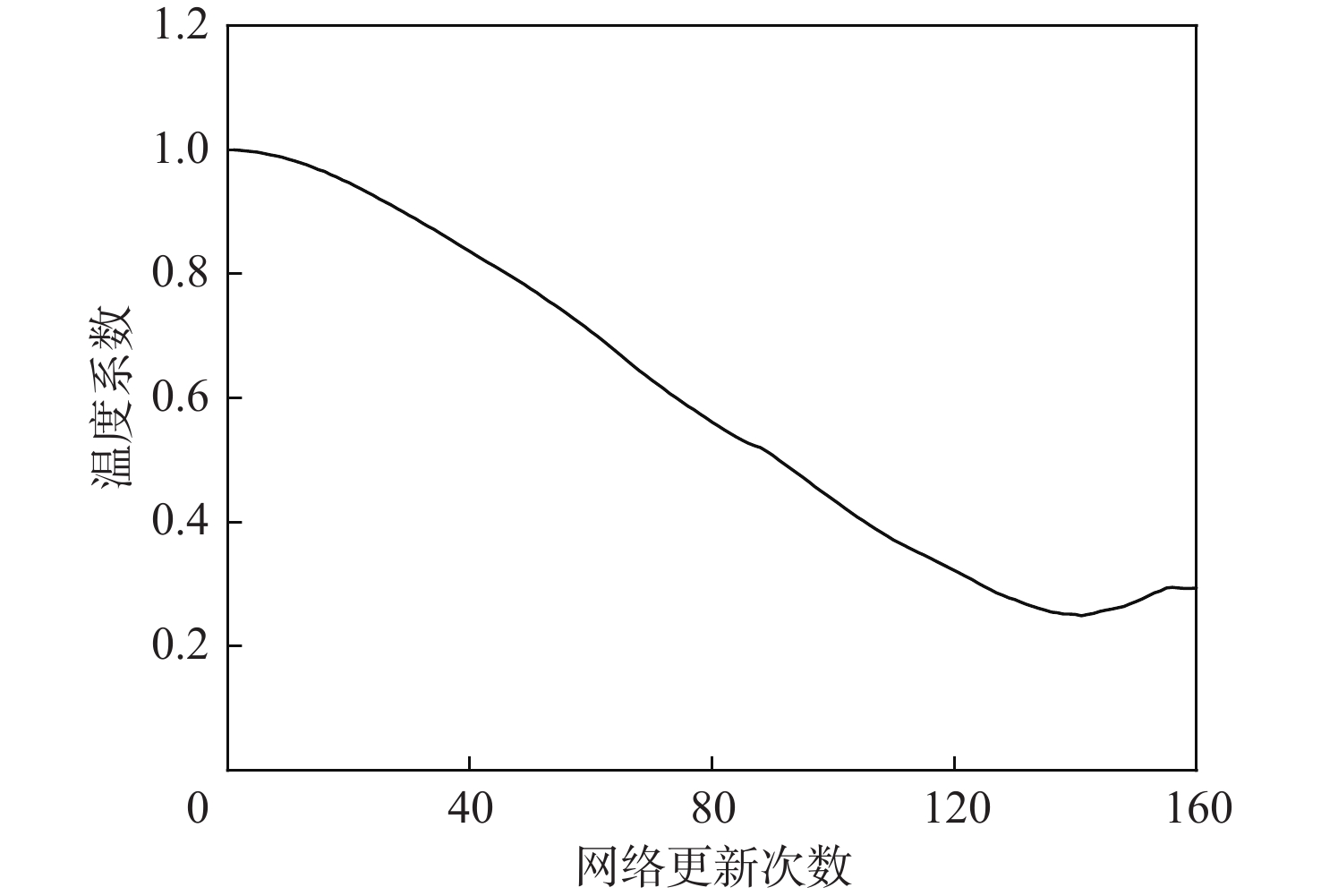
超参数	数值
经验缓存池大小 $\left\| \mathcal{D} \right\|$	5000
采样经验大小 ${M}$	128
折扣率 $\gamma$	0.98
学习率 $\alpha$	0.0005
期望熵 ${{H}_0}$	−5
温度系数 $\tau$	1
平滑常数 $\epsilon$	0.005
网络更新频率 ${N}$	60

下载: 导出CSV

表 4 不同制导律下的终端参数

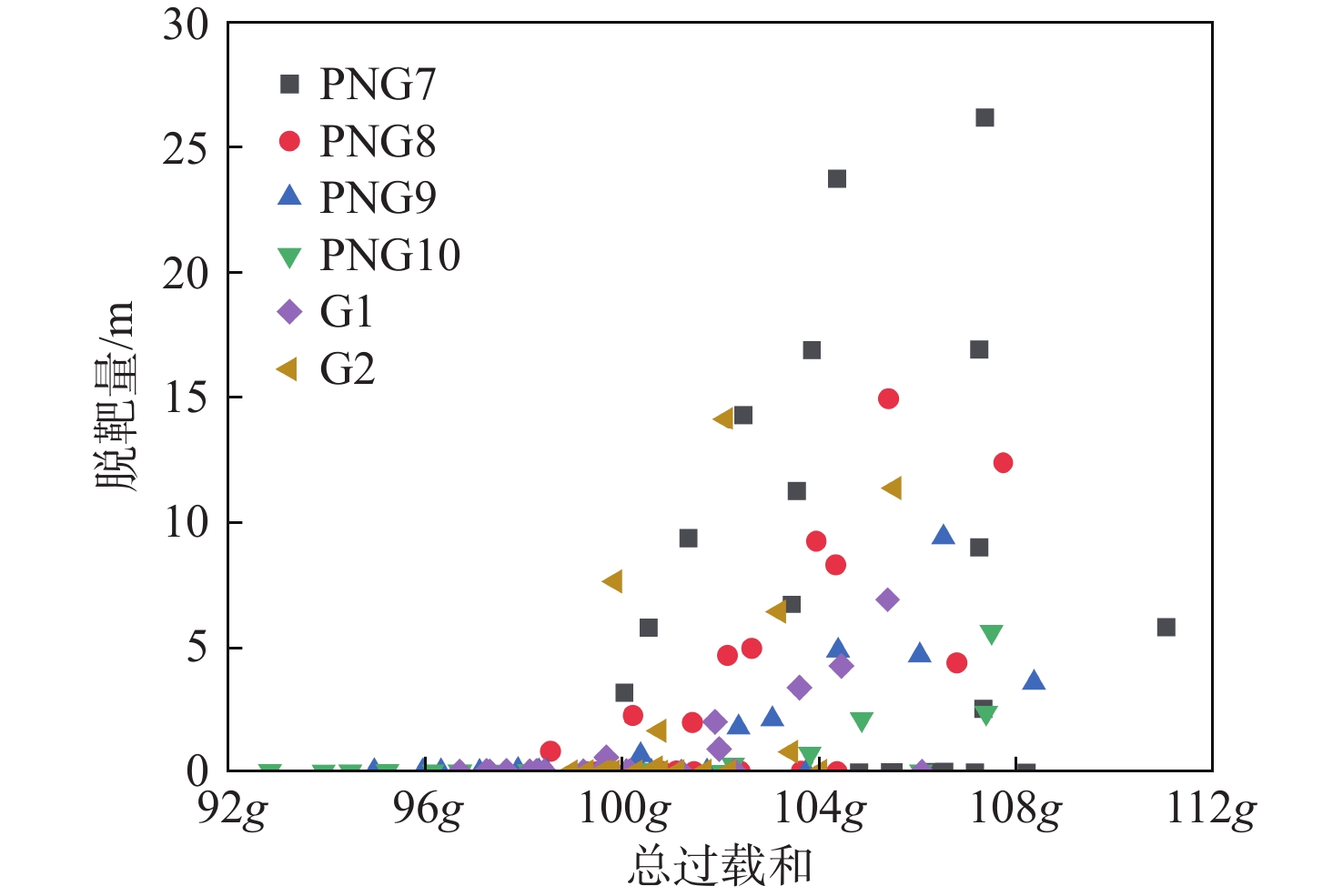
Table 4. Terminal parameters with different guidance laws

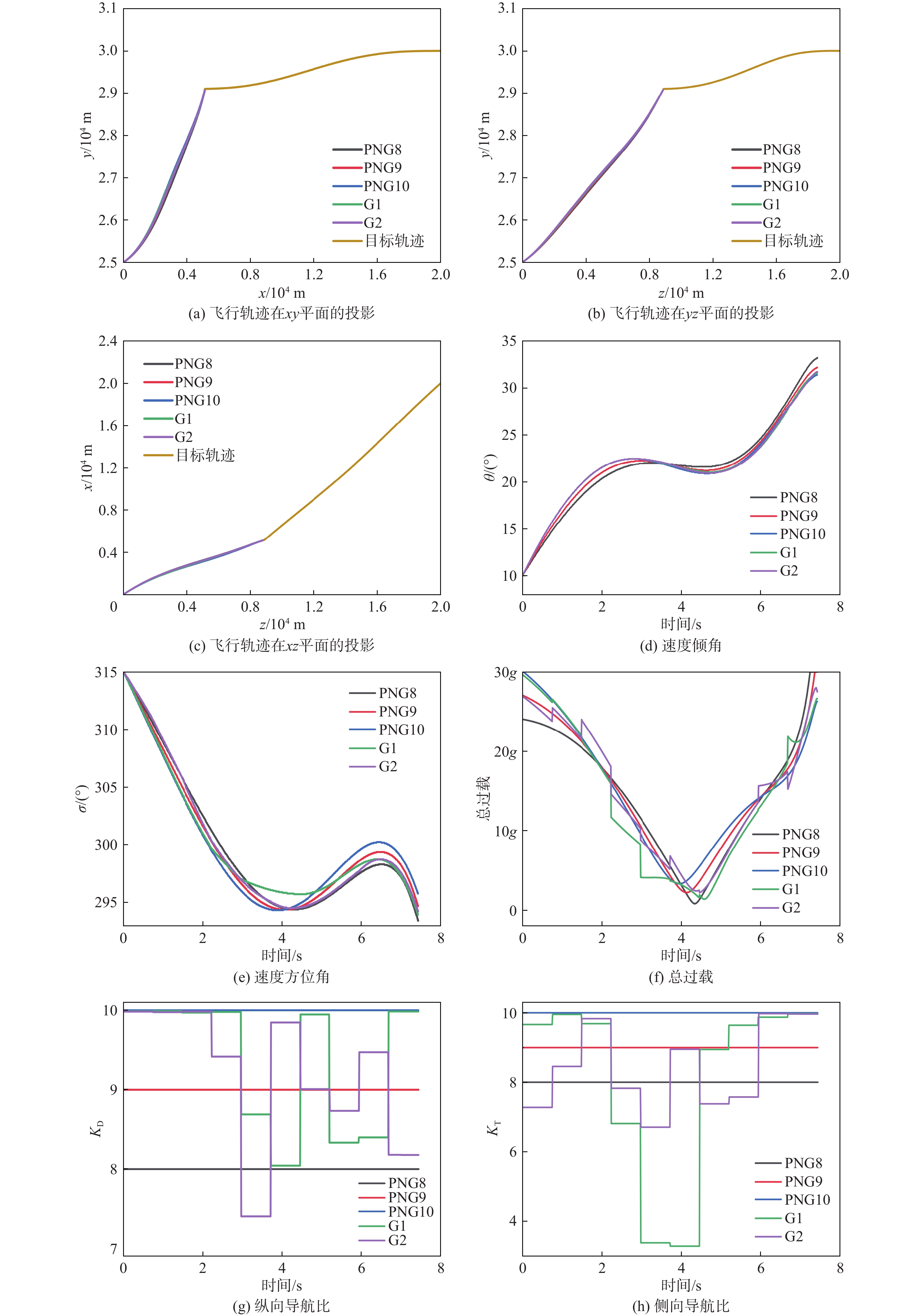
制导律	飞行时间/s	脱靶量/m	总过载和
PNG7	7.439	2.974	107.217 g
PNG8	7.435	0.780	108.323 g
PNG9	7.432	0.263	110.543 g
PNG10	7.430	0.113	112.474 g
G1	7.430	0.220	103.326 g
G2	7.432	0.248	109.267 g

下载: 导出CSV

表 5 未训练场景下蒙特卡罗结果统计

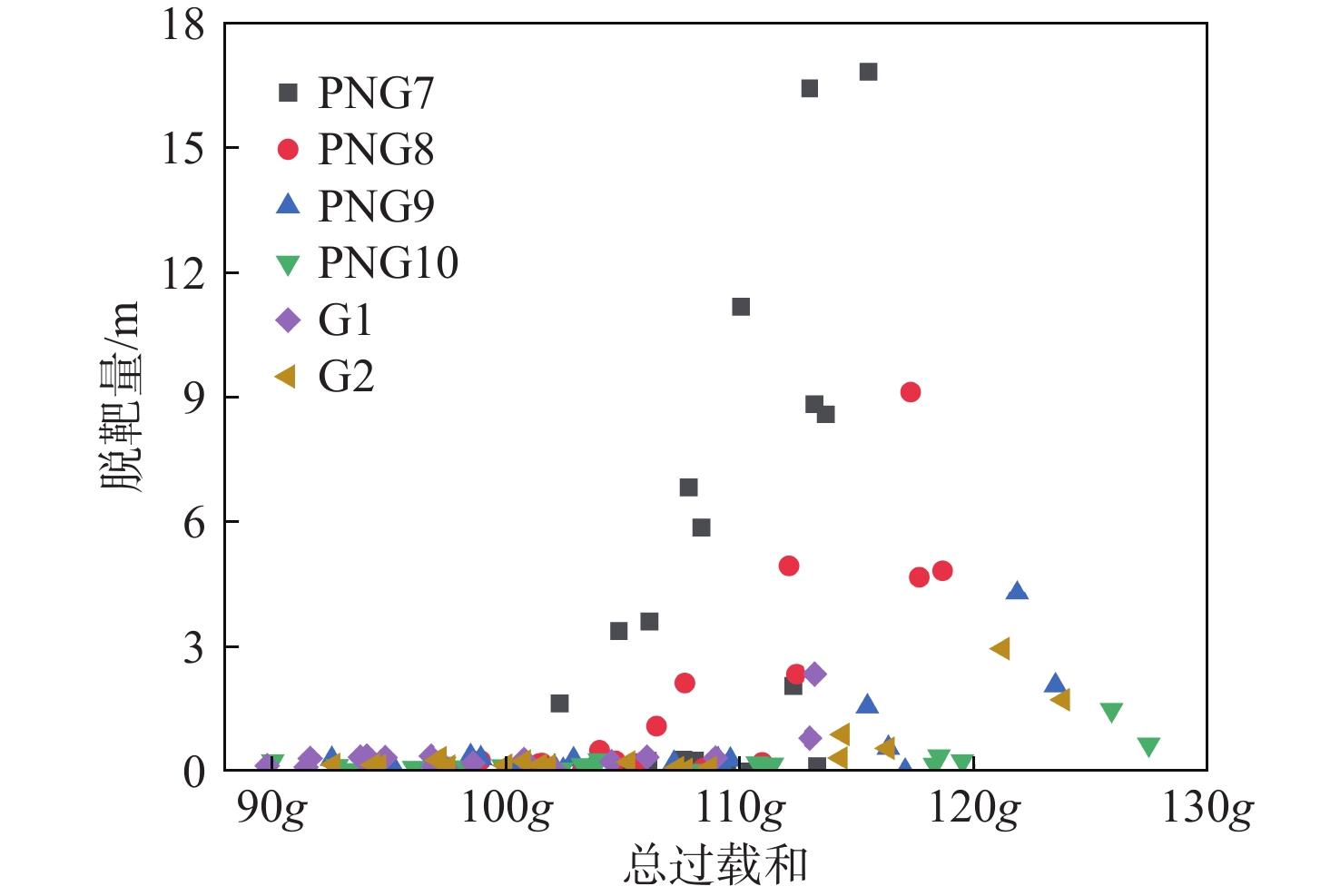
Table 5. Monte Carlo results statistics in untrained scenarios

制导律	脱靶量均值/m	脱靶量方差/m²	总过载和均值
PNG7	1.793	2.504	105.983 g
PNG8	0.380	0.116	104.811 g
PNG9	0.192	0.012	105.242 g
PNG10	0.187	0.012	106.297 g
G1	0.189	0.012	98.532 g
G2	0.188	0.018	104.906 g

下载: 导出CSV

参考文献(18)

[1]	纪毅, 王伟, 张宏岩, 等. 面向高机动目标拦截任务的空空导弹制导方法综述[J]. 航空兵器, 2022, 29(6): 15-25. doi: 10.12132/ISSN.1673-5048.2022.0119 JI Y, WANG W, ZHANG H Y, et al. A survey on guidance method of air-to-air missiles facing high maneuvering targets[J]. Aero Weaponry, 2022, 29(6): 15-25(in Chinese). doi: 10.12132/ISSN.1673-5048.2022.0119
[2]	JEON I S, KARPENKO M, LEE J I. Connections between proportional navigation and terminal velocity maximization guidance[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(2): 383-388. doi: 10.2514/1.G004672
[3]	ZHANG B L, ZHOU D. Optimal predictive sliding-mode guidance law for intercepting near-space hypersonic maneuvering target[J]. Chinese Journal of Aeronautics, 2022, 35(4): 320-331. doi: 10.1016/j.cja.2021.05.021
[4]	LI C D, WANG J, HE S M, et al. Collision-geometry-based generalized optimal impact angle guidance for various missile and target motions[J]. Aerospace Science and Technology, 2020, 106: 106204. doi: 10.1016/j.ast.2020.106204
[5]	YE D, SHI M M, SUN Z W. Satellite proximate interception vector guidance based on differential games[J]. Chinese Journal of Aeronautics, 2018, 31(6): 1352-1361. doi: 10.1016/j.cja.2018.03.012
[6]	郭建国, 胡冠杰, 郭宗易, 等. 天线罩误差下基于ADP的机动目标拦截制导策略[J]. 宇航学报, 2022, 43(7): 911-920. doi: 10.3873/j.issn.1000-1328.2022.07.007 GUO J G, HU G J, GUO Z Y, et al. ADP-based guidance strategy for maneuvering target interception under radome errors[J]. Journal of Astronautics, 2022, 43(7): 911-920(in Chinese). doi: 10.3873/j.issn.1000-1328.2022.07.007
[7]	白志会, 黎克波, 苏文山, 等. 现实真比例导引拦截任意机动目标捕获区域[J]. 航空学报, 2020, 41(8): 323947. BAI Z H, LI K B, SU W S, et al. Capture region of RTPN guidance law against arbitrarily maneuvering targets[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(8): 323947(in Chinese).
[8]	王荣刚, 唐硕. 拦截高速运动目标广义相对偏置比例制导律[J]. 西北工业大学学报, 2019, 37(4): 682-690. doi: 10.3969/j.issn.1000-2758.2019.04.006 WANG R G, TANG S. Intercepting higher-speed targets using generalized relative biased proportional navigation[J]. Journal of Northwestern Polytechnical University, 2019, 37(4): 682-690(in Chinese). doi: 10.3969/j.issn.1000-2758.2019.04.006
[9]	LI K B, SHIN H S, TSOURDOS A, et al. Capturability of 3D PPN against lower-speed maneuvering target for homing phase[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(1): 711-722. doi: 10.1109/TAES.2019.2938601
[10]	SHIN H S, LI K B. An improvement in three-dimensional pure proportional navigation guidance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 3004-3014. doi: 10.1109/TAES.2021.3067656
[11]	张秦浩, 敖百强, 张秦雪. Q-learning强化学习制导律[J]. 系统工程与电子技术, 2020, 42(2): 414-419. doi: 10.3969/j.issn.1001-506X.2020.02.21 ZHANG Q H, AO B Q, ZHANG Q X. Reinforcement learning guidance law of Q-learning[J]. Systems Engineering and Electronics, 2020, 42(2): 414-419(in Chinese). doi: 10.3969/j.issn.1001-506X.2020.02.21
[12]	李庆波, 李芳, 董瑞星, 等. 利用强化学习开展比例导引律的导航比设计[J]. 兵工学报, 2022, 43(12): 3040-3047. doi: 10.12382/bgxb.2021.0631 LI Q B, LI F, DONG R X, et al. Navigation ratio design of proportional navigation law using reinforcement learning[J]. Acta Armamentarii, 2022, 43(12): 3040-3047(in Chinese). doi: 10.12382/bgxb.2021.0631
[13]	邱潇颀, 高长生, 荆武兴. 拦截大气层内机动目标的深度强化学习制导律[J]. 宇航学报, 2022, 43(5): 685-695. doi: 10.3873/j.issn.1000-1328.2022.05.013 QIU X Q, GAO C S, JING W X. Deep reinforcement learning guidance law for intercepting endo-atmospheric maneuvering targets[J]. Journal of Astronautics, 2022, 43(5): 685-695(in Chinese). doi: 10.3873/j.issn.1000-1328.2022.05.013
[14]	CHEN W X, GAO C S, JING W X. Proximal policy optimization guidance algorithm for intercepting near-space maneuvering targets[J]. Aerospace Science and Technology, 2023, 132: 108031. doi: 10.1016/j.ast.2022.108031
[15]	HE S M, SHIN H S, TSOURDOS A. Computational missile guidance: a deep reinforcement learning approach[J]. Journal of Aerospace Information Systems, 2021, 18(8): 571-582. doi: 10.2514/1.I010970
[16]	GAUDET B, FURFARO R, LINARES R. Reinforcement learning for angle-only intercept guidance of maneuvering targets[J]. Aerospace Science and Technology, 2020, 99: 105746. doi: 10.1016/j.ast.2020.105746
[17]	HAARNOJA T, ZHOU A, ABBEEL P, et al. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor[C]//Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018, 80: 1861-1870.
[18]	HAARNOJA T, ZHOU A, HARTIKAINEN K, et al. Soft actor-critic algorithms and applications[EB/OL]. (2019-01-29)[2023-06-01]. https://arxiv.org/abs/1812.05905v2.