考虑紧急订货的系统备件费用优化建模与求解

崔新豪; 杨锐意; 张思悦; 杨丽颖; 陈练; 肖依永

doi:10.13700/j.bh.1001-5965.2023.0583

考虑紧急订货的系统备件费用优化建模与求解

doi: 10.13700/j.bh.1001-5965.2023.0583

1.
北京航空航天大学可靠性与系统工程学院，北京 100191
2.
核工业理化工程研究院，天津 300180
3.
中国船舶集团有限公司第七一四研究所，北京 100101

基金项目:

国家自然科学基金委员会-中国民用航空局民航联合研究基金(U2233214)；国家自然科学基金(71871003)

详细信息

通讯作者:
E-mail：xiaoyiyong@buaa.edu.cn

中图分类号: V37；V241.0
计量
- 文章访问数: 197
- HTML全文浏览量: 69
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-14
- 录用日期: 2023-10-13
- 网络出版日期: 2023-11-01
- 整期出版日期: 2025-11-25

Modeling and solution of spare parts costs for complex systems considering emergency order strategy

1.
School of Reliability and Systems Engineering，Beihang University，Beijing 100191，China
2.
Research Institute of Physical and Chemical Engineering of Nuclear Industry，Tianjin 300180，China
3.
The 714 Research Institute of CSSC，Beijing 100101，China

Funds:

NSFC-Civil Aviation Joint Research Fund (U2233214)；National Natural Science Foundation of China (71871003)

More Information

Corresponding author: E-mail：xiaoyiyong@buaa.edu.cn

摘要

摘要:
针对不确定需求下常规订购与紧急订货策略耦合所导致的备件总费用优化中存在的问题，提出一种结合马尔可夫链需求预测与紧急订货策略的备件订购费用优化方法。进一步针对该问题，提出了考虑紧急订货的复杂系统备件费用优化模型，并以混合整数线性规划的形式进行建模与求解。该模型考虑了紧急订货策略对复杂系统备件订购方式的影响，以备件综合费用最小化为目标，获得最佳订购模式选择与对应数量。以某复杂系统在实际应用场景中的数据为例，对所建模型进行应用验证，发现在采用紧急订货策略后，备件总成本降低了29.56万元，其中库存保管费用降低了40.63%。证明所提优化模型可以在有效降低备件成本，提升系统经济效益，为复杂系统经济性工程提供备件费用优化方面的技术方法支持。
- 备件管理 /
- 紧急订货 /
- 马尔可夫链 /
- 保障概率 /
- 优化模型 /
- 经济性
Abstract:
Reducing the comprehensive cost of spare parts is one of the main objectives of cost optimization research in the support phase of complex systems. Especially in uncertain scenarios, such as large-scale equipment training and batch production of newly developed products, the demand for spare parts and the associated cost changes are harder to predict. Therefore, a Markov chain can be used to predict demand and complete the ordering process in combination with the emergency order strategy. However, there is a coupling effect between regular and emergency orders, which affects the total spare parts cost, creating a complex optimization problem. To address this issue, this paper proposes an optimization model and solves it using mixed integer linear programming. Finally, the model is applied and validated using data from a real-world scenario. The results show that the total cost is reduced by 295,600 yuan, with a 40.63% reduction in inventory storage costs. This demonstrates that the proposed model effectively lowers spare parts costs, improves system economic efficiency, and provides technical support for optimizing spare parts costs in complex systems.
- spare parts management /
- emergency order /
- Markov chain /
- guarantee probability /
- optimization model /
- economic efficiency

HTML全文

图 1 复杂系统框图结构示例

Figure 1. Example of complex system block structure

下载: 全尺寸图片幻灯片

图 2 备件数量状态转移图

Figure 2. State transition of spare parts quantity

下载: 全尺寸图片幻灯片

图 3 备件数量计算流程图

Figure 3. Process for calculating spare parts quantity

下载: 全尺寸图片幻灯片

图 4 紧急订货策略示意图

Figure 4. Emergency order strategy

下载: 全尺寸图片幻灯片

图 5 五备件系统的功能逻辑图

Figure 5. Functional logic diagram of five spare parts system

下载: 全尺寸图片幻灯片

图 6 AMPL求解逻辑框架图

Figure 6. Solution logic framework of AMPL

下载: 全尺寸图片幻灯片

表 1 备件最低库存水平

Table 1. Minimum inventory level of spare parts

备件类型i	最低库存水平H_i
1	5
2	5
3	5
4	30
5	10

下载: 导出CSV

表 2 稳态概率结果

Table 2. Steady-state probability results

π(s₀, s₁)	稳态概率值
π(1, 1)	0.25
π(1, 2)	0.25
π(2, 1)	0.25
π(2, 2)	0.25

下载: 导出CSV

表 3 状态转移概率结果

Table 3. State transition probability results

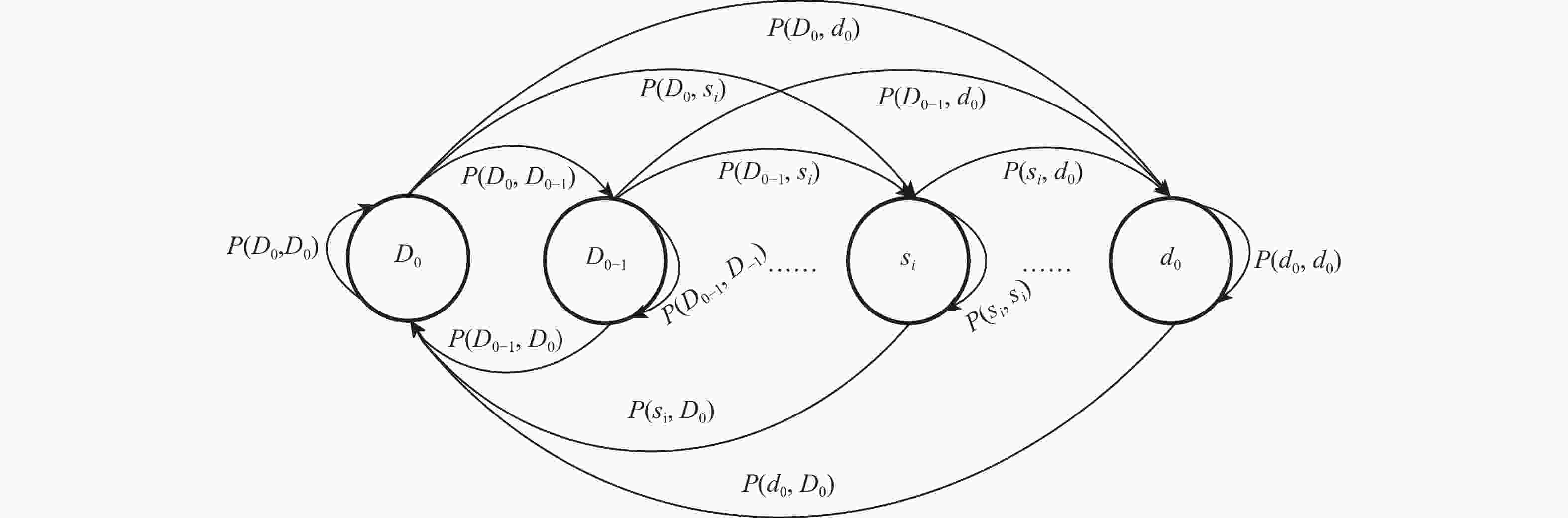
转移前状态(1,1)				转移前状态(1,2)				转移前状态(2,1)				转移前状态(2,2)
转移后(1,1)	(1,2)	(2,1)	(2,2)	转移后(1,1)	(1,2)	(2,1)	(2,2)	转移后(1,1)	(1,2)	(2,1)	(2,2)	转移后(1,1)	(1,2)	(2,1)	(2,2)
0.5977	0.0371	0.3651	0	0.0371	0.5977	0	0.3651	0.3651	0	0.5977	0.0371	0	0.3651	0.0371	0.5977

下载: 导出CSV

表 4 备件数量消耗结果

Table 4. Consumption results of spare parts quantity

备件类型i	第1期间消耗	第2期间消耗	第3期间消耗	第4期间消耗	第5期间消耗	第6期间消耗	第7期间消耗	第8期间消耗	第9期间消耗	第10期间消耗	第11期间消耗	第12期间消耗
1	11	15	13	12	16	17	14	12	9	9	8	17
2	6	7	8	9	8	11	7	5	7	6	10	12
3	4	7	4	8	7	7	4	4	5	3	6	2
4	69	63	46	93	70	60	68	72	49	88	47	69
5	14	10	18	14	11	15	12	16	9	12	11	8

下载: 导出CSV

表 5 补充备件费用数据

Table 5. Supplementary spare parts cost data

备件类型i	库存保管费用率	常规订货单价/万元	紧急订货单价/万元
1	3.5	0.4	0.5
2	4.2	0.6	0.7
3	3.8	0.5	0.53
4	4.5	0.15	0.2
5	5.0	0.45	0.6

下载: 导出CSV

表 6 优化模型输出结果

Table 6. Optimization model output

备件模型i	常规/紧急订货数量
备件模型i	第1期间	第2期间	第3期间	第4期间	第5期间	第6期间	第7期间	第8期间	第9期间	第10期间	第11期间	第12期间
1	0/0	10/0	13/0	12/0	16/0	17/0	14/0	12/0	9/0	9/0	8/0	17/0
2	0/5	2/3	5/0	9/0	8/0	11/0	7/0	5/0	7/0	6/0	10/0	12/0
3	0/5	2/3	1/4	4/1	6/0	7/0	4/0	4/0	4/1	2/3	3/2	0/5
4	0/30	33/0	46/0	93/0	70/0	60/0	68/0	72/0	49/0	88/0	47/0	69/0
5	2/8	2/8	10/0	14/0	11/0	15/0	12/0	16/0	9/1	11/0	11/0	8/2
注：黑体为备件紧急订货数量。

下载: 导出CSV

参考文献(24)

[1]	杜燕. A航空公司航材管理与成本优化研究[D]. 上海: 上海交通大学, 2015. DU Y. A Research on air material management and cost optimization of A airlines[D]. Shanghai: Shanghai Jiao Tong University, 2015(in Chinese).
[2]	李巧君. 基于蚁群算法和极限学习机的舰船电子装备备件优化模型[J]. 舰船科学技术, 2022, 44(5): 158-161. doi: 10.3404/j.issn.1672-7649.2022.05.034 LI Q J. Optimization model of ship electronic equipment spare parts based on ant colony algorithm and limit learning machine[J]. Ship Science and Technology, 2022, 44(5): 158-161(in Chinese). doi: 10.3404/j.issn.1672-7649.2022.05.034
[3]	吕川, 赵宇, 张坚. 飞机备件需求量的确定方法[J]. 北京航空航天大学学报, 1995, 21(4): 130-133. LYU C, ZHAO Y, ZHANG J. Method for determining the spares demand of airliner[J]. Journal of Beijing University of Aeronautics and Astronautics, 1995, 21(4): 130-133(in Chinese).
[4]	董彦军. 航空备件需求预测及两级供应保障策略研究[D]. 沈阳: 沈阳航空航天大学, 2014: 9-10. DONG Y J. Demand prediction of aircraft spare parts and guarantee strategy of two stages research[D]. Shenyang: Shenyang Aerospace University, 2014: 9-10(in Chinese).
[5]	瞿红春, 姜柏松. 基于航材系统保障率的备件优化模型的研究[J]. 航空制造技术, 2004, 47(9): 79-82,87. doi: 10.3969/j.issn.1671-833X.2004.09.019 QU H C, JIANG B S. Study on the aeronautical material system reliability based optimization model of spare parts[J]. Aeronautical Manufacturing Technology, 2004, 47(9): 79-82,87(in Chinese). doi: 10.3969/j.issn.1671-833X.2004.09.019
[6]	康子旭, 周栋, 李会欣, 等. 基于飞机状态的备件动态规划技术[J]. 北京航空航天大学学报, 2024, 50(1): 276-285. KANG Z X, ZHOU D, LI H X, et al. Dynamic planning technology of civil spare parts based on aircraft state[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(1): 276-285(in Chinese).
[7]	董骁雄, 陈云翔, 项华春, 等. 基于SST和Bayes的初始备件需求确定方法[J]. 北京航空航天大学学报, 2018, 44(2): 316-321. DONG X X, CHEN Y X, XIANG H C, et al. Determination method of initial spares requirement based on SST and Bayes theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 316-321(in Chinese).
[8]	HU Q W, BOYLAN J E, CHEN H J, et al. OR in spare parts management: a review[J]. European Journal of Operational Research, 2018, 266(2): 395-414. doi: 10.1016/j.ejor.2017.07.058
[9]	HARTANTO D, AGUSTINITA A. Model of delivery consolidation of critical spare part: case study of an oil and gas company[J]. IOP Conference Series: Materials Science and Engineering. Denpasar: IOP Publishing, 2018, 337(1): 012021.
[10]	龙军, 康锐, 马麟, 等. 任意寿命分布的多部件系统备件配置优化算法[J]. 北京航空航天大学学报, 2007, 33(6): 698-700. doi: 10.3969/j.issn.1001-5965.2007.06.016 LONG J, KANG R, MA L, et al. Algorithm for spares optimization of system with multi-items with different life distributions[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(6): 698-700(in Chinese). doi: 10.3969/j.issn.1001-5965.2007.06.016
[11]	郑长征, 刘志学, 刘丹. 考虑备件随机折损的备件订货与设备维修策略[J]. 计算机集成制造系统, 2010, 16(10): 2129-2138. ZHENG C Z, LIU Z X, LIU D. Replenishment and equipment maintenance policices considering stochastic spare parts deterioration[J]. Computer Integrated Manufacturing Systems. 2010, 16(10): 2129-2138(in Chinese).
[12]	SHAFIEE M, SORENSEN J D. Maintenance optimization and inspection planning of wind energy assets: models, methods and strategies[J]. Reliability Engineering & System Safety, 2019, 192: 105993.
[13]	CANTINI A, PERON M, DE CARLO F, et al. A decision support system for configuring spare parts supply chains considering different manufacturing technologies[J]. International Journal of Production Research, 2024, 62(8): 3023-3043. doi: 10.1080/00207543.2022.2041757
[14]	毕义明, 王汉功. 武器装备损耗备件预测模型研究[J]. 装备指挥技术学院学报, 2004, 15(1): 1-4. BI Y M, WANG H G. Research on the consumption standard model of weapon's equipment spare[J]. Journal of Institute of Command and Technology, 2004, 15(1): 1-4(in Chinese).
[15]	YE Y, LU Y G, ROBINSON P, et al. An empirical Bayes approach to incorporating demand intermittency and irregularity into inventory control[J]. European Journal of Operational Research, 2022, 303(1): 255-272. doi: 10.1016/j.ejor.2022.02.033
[16]	BABAI M Z, CHEN H, SYNTETOS A A, et al. A compound-Poisson Bayesian approach for spare parts inventory forecasting[J]. International Journal of Production Economics, 2021, 232: 107954. doi: 10.1016/j.ijpe.2020.107954
[17]	CHANDRIAH K K, NARAGANAHALLI R V. RNN/LSTM with modified Adam optimizer in deep learning approach for automobile spare parts demand forecasting[J]. Multimedia Tools and Applications, 2021, 80(17): 26145-26159. doi: 10.1007/s11042-021-10913-0
[18]	杜文超, 何曙光, 边德军, 等. 二维质保下基于使用强度的备件库存策略研究[J]. 工业工程与管理, 2017, 22(2): 119-124,131. DU W C, HE S G, BIAN D J, et al. Inventory control policy for parts concerning the usage rate’s effect to product reliability of two-dimensional warranty[J]. Industrial Engineering and Management, 2017, 22(2): 119-124,131(in Chinese).
[19]	陈顶, 方志耕, 刘思峰. 可修排队系统备件灰色生灭预测模型[J]. 系统工程理论与实践, 2020, 40(5): 1326-1338. doi: 10.12011/1000-6788-2017-1091-13 CHEN D, FANG Z G, LIU S F. Grey BD prediction model for spare parts of repairable queuing system[J]. Systems Engineering —Theory & Practice, 2020, 40(5): 1326-1338(in Chinese). doi: 10.12011/1000-6788-2017-1091-13
[20]	袁园, 付兴方, 吴佳康. 基于平均备件保障概率的备件库存优化模型研究[J]. 舰船电子工程, 2018, 38(10): 156-159. doi: 10.3969/j.issn.1672-9730.2018.10.039 YUAN Y, FU X F, WU J K. Optimization model on inventory based on average support probability of spare part[J]. Ship Electronic Engineering, 2018, 38(10): 156-159(in Chinese). doi: 10.3969/j.issn.1672-9730.2018.10.039
[21]	TAGARAS G, VLACHOS D. A periodic review inventory system with emergency replenishments[J]. Management Science, 2001, 47(3): 415-429. doi: 10.1287/mnsc.47.3.415.9770
[22]	吴茜茜, 赵慧慧, 郝晶晶. 考虑退货影响的概率销售下的库存问题研究[J]. 合肥工业大学学报(自然科学版), 2023, 46(2): 280-284. WU Q Q, ZHAO H H, HAO J J. A Study of inventory problem for probabilistic selling with return[J]. Journal Of Hefei University of Technology (Natural Science), 2023, 46(2): 280-284(in Chinese).
[23]	肖依永, 常文兵, 周晟瀚, 等. 现代装备系统经济性工程—理论、方法与应用[M]. 北京: 科学出版社, 2021: 165-173. XIAO Y Y, CHANG W B, ZHOU S H, et al. Economic engineering of modern equipment systems-theory, method, and application[M]. Beijing: Science Press, 2021: 165-173 (in Chinese).
[24]	ZHENG M M, YE H Q, WANG D, et al. Joint optimization of condition-based maintenance and spare parts orders for multi-unit systems with dual sourcing[J]. Reliability Engineering & System Safety, 2021, 210: 107512.