曲面等值分割几何认知计算方法

胡靖尘; 郑国磊

doi:10.13700/j.bh.1001-5965.2023.0593

曲面等值分割几何认知计算方法

doi: 10.13700/j.bh.1001-5965.2023.0593

胡靖尘,
郑国磊^,

北京航空航天大学机械工程及自动化学院，北京 100191

详细信息

通讯作者:
E-mail：zhengguolei@buaa.edu.cn

中图分类号: V260.5
计量
- 文章访问数: 203
- HTML全文浏览量: 68
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-19
- 录用日期: 2024-02-08
- 网络出版日期: 2024-02-26
- 整期出版日期: 2025-11-25

Geometric cognitive computing method for sculptured surface iso-segmentation

HU Jingchen,
ZHENG Guolei^,

School of Mechanical Engineering & Automation，Beihang University，Beijing 100191，China

More Information

Corresponding author: E-mail：zhengguolei@buaa.edu.cn

摘要

摘要:
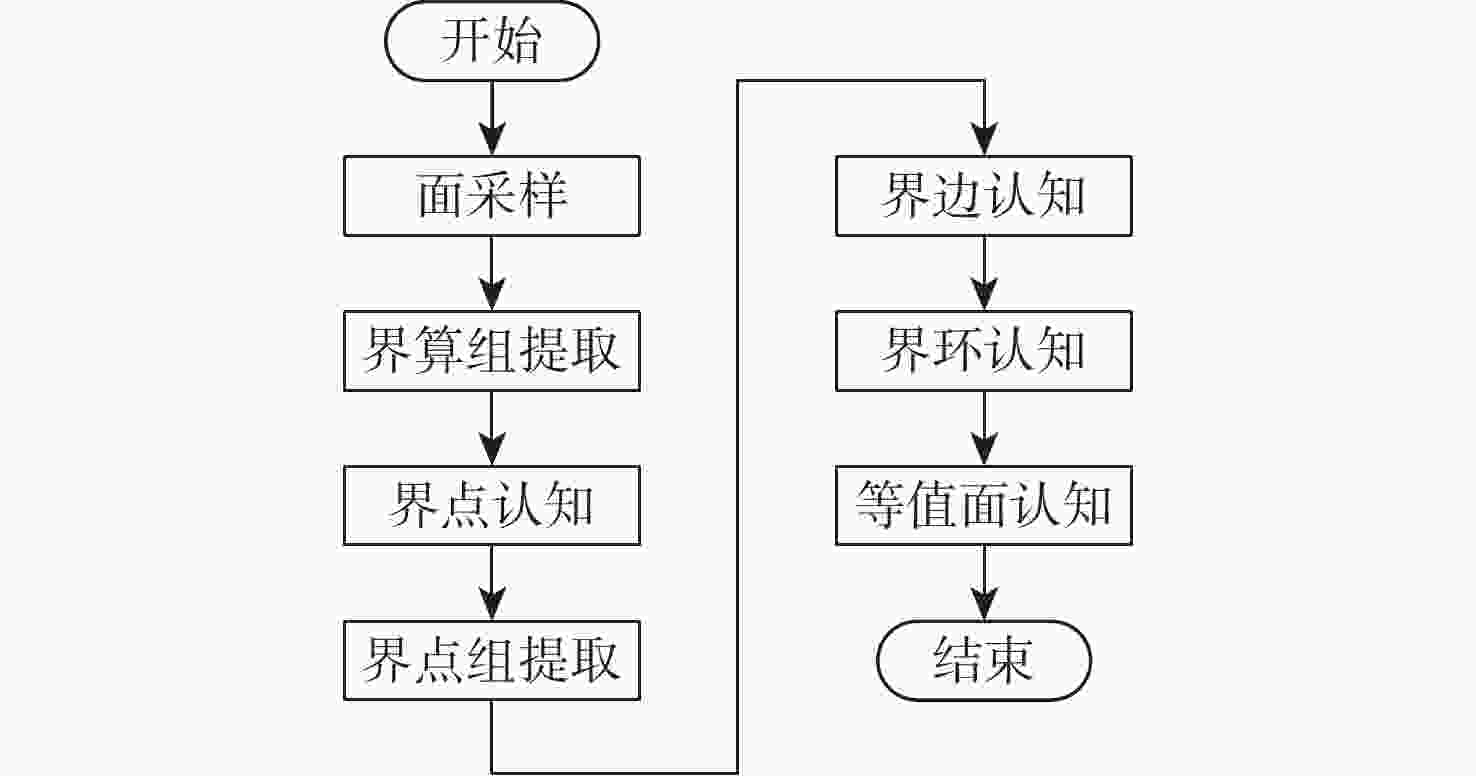
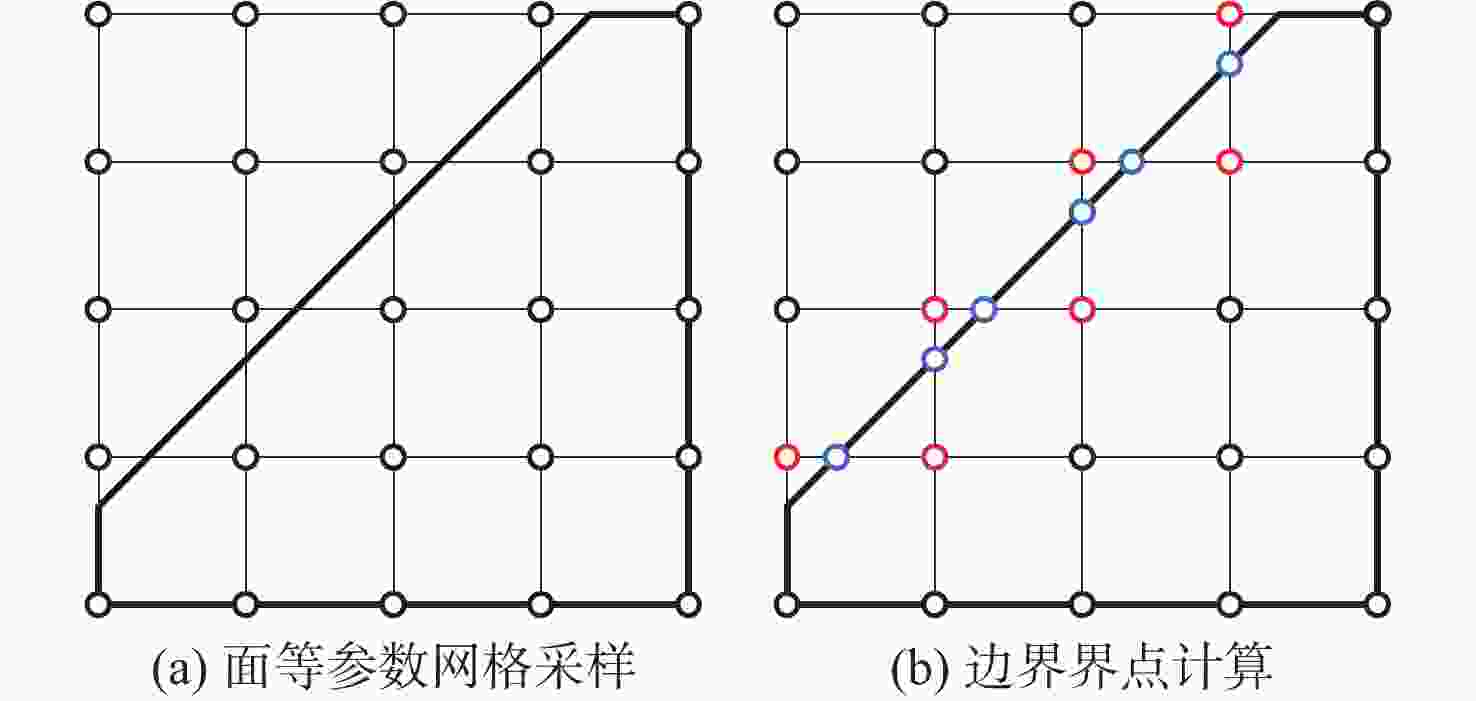
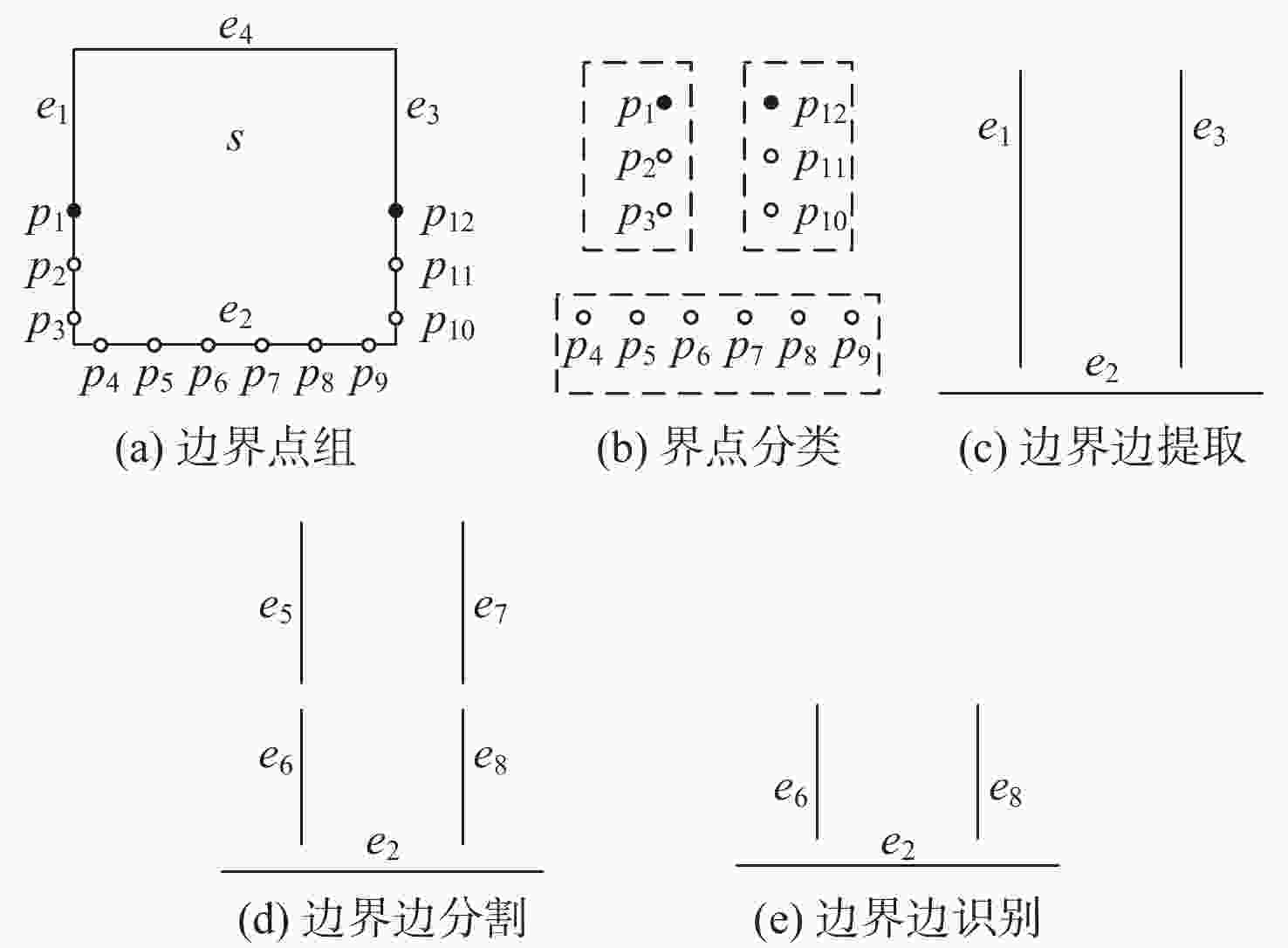
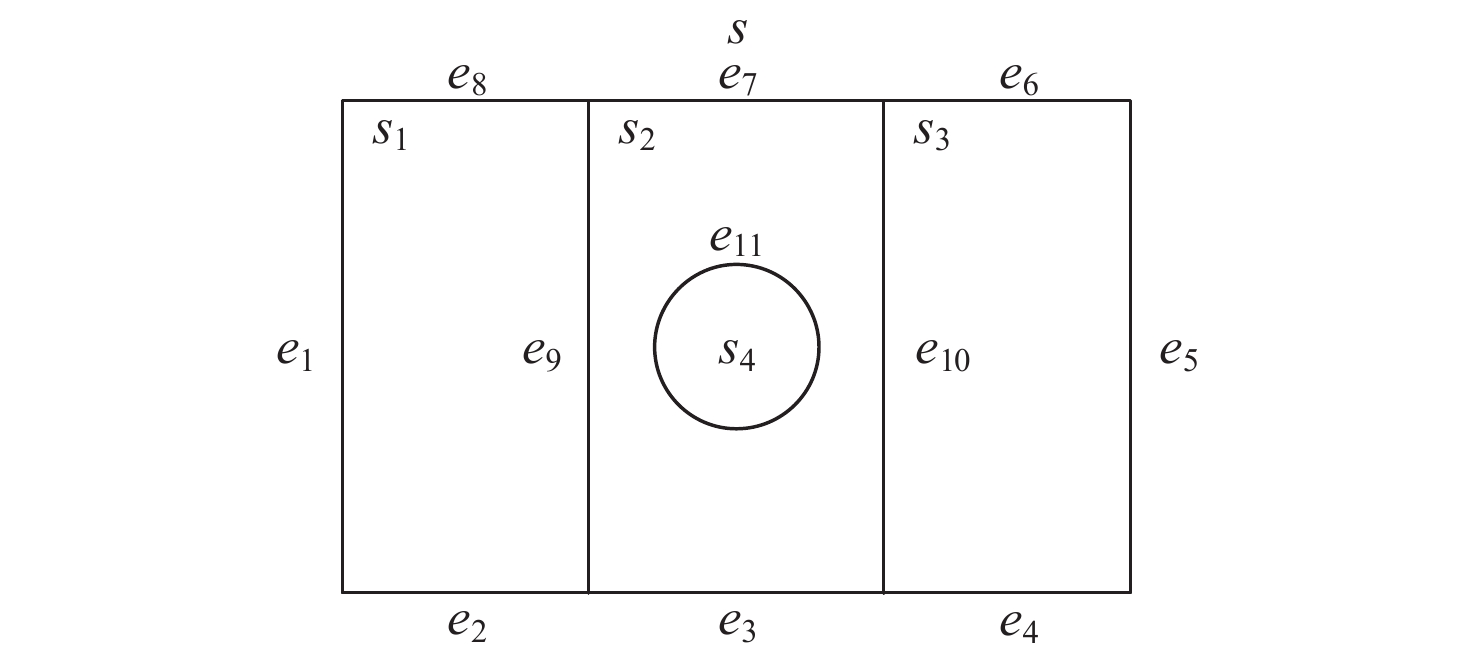
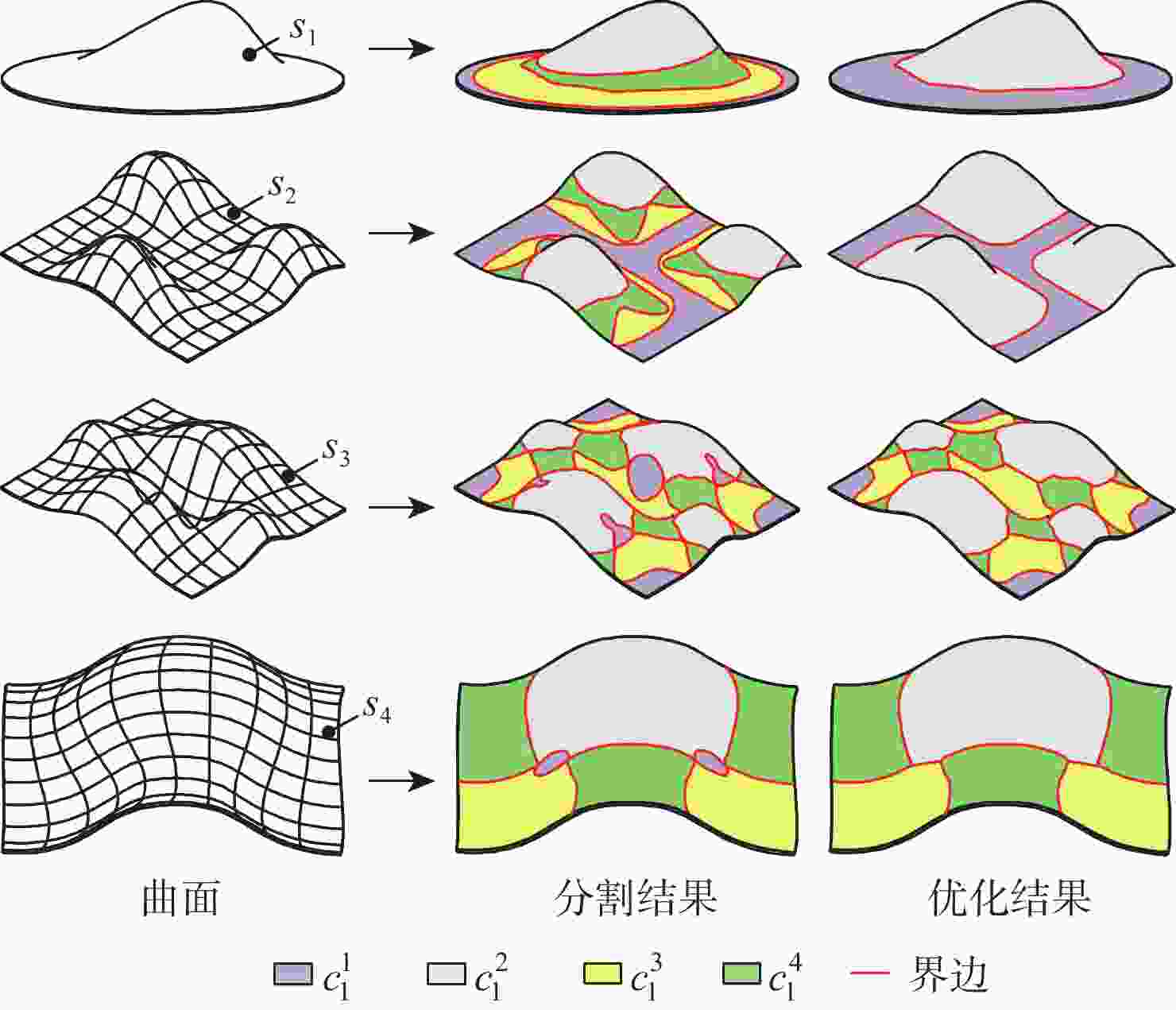
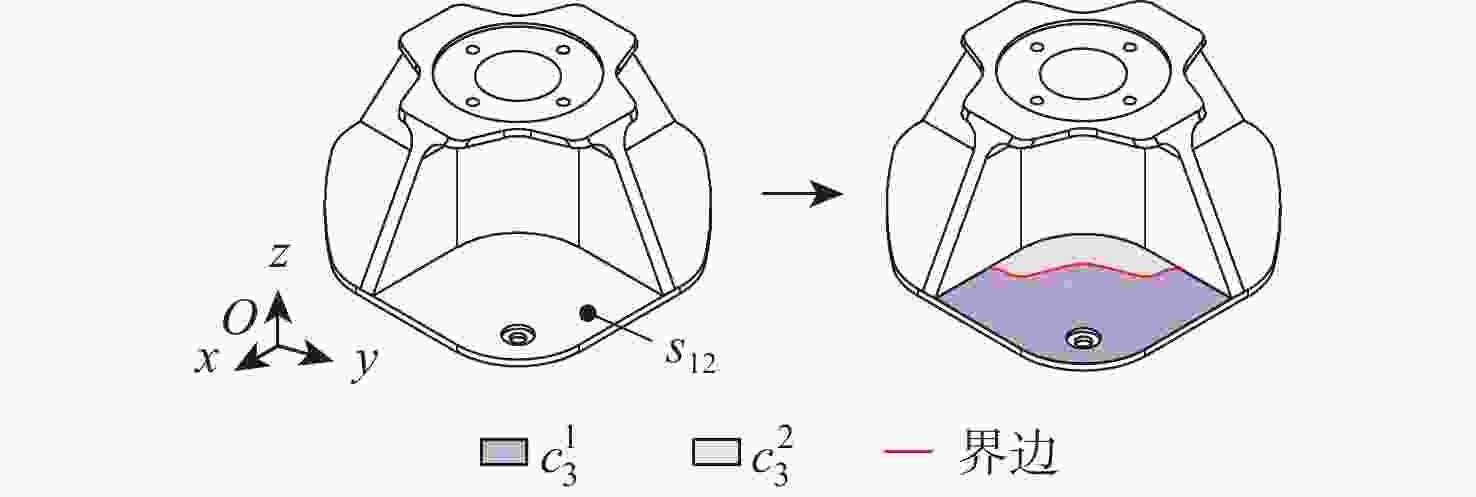
基于界点跟踪的曲面等值分割方法具有通用性，但复杂曲面等值分割效率较低。为此，提出曲面等值分割几何认知计算方法。对输入面进行等参数网格采样并计算边界界点；从采样点中提取界算组并计算、识别界点；从界点中提取界点组并构造、识别界边；从界边中提取、识别内界环，以此分割输入面并对所得等值面进行识别。以主曲率、高斯曲率、平均曲率和可加工性为面点属性设计分割条件集并进行大量实例测试。实验结果表明：所提方法的分割效率比现有方法平均提高了38.44%，所提方法在复杂曲面分割应用中具有较高的分割效率。
- 曲面等值分割 /
- 几何认知计算 /
- 界点 /
- 界边 /
- 界环
Abstract:
Sculptured surface iso-segmentation method based on boundary point tracking has applicability to different segmentation situations. However, it exhibits low efficiency in the application of sculptured surface iso-segmentation. Therefore, this paper presents a geometric cognitive computing algorithm for surface iso-segmentation. Firstly, the input surface is sampled by isoparametric grid sampling, and then the boundary points are calculated. Secondly, the boundary point calculation group is extracted from the sampling points, and then the boundary points are calculated and recognized. Thirdly, the boundary point group is extracted from the boundary points, and then the boundary edges are constructed and recognized. Finally, the inner boundary loop is extracted and recognized from the boundary edges to split the input surface, and the resulting iso-surfaces are recognized. Attributes including principal curvatures, Gaussian curvature, mean curvature, and machinability are used to design a condition set for the iso-segmentation of several surfaces. The segmentation efficiency of the proposed method is 38.44% higher than that of the existing method. Test results show that the proposed method can achieve higher segmentation efficiency in the application of sculptured surface iso-segmentation.
- sculptured surface iso-segmentation /
- geometric cognitive computing /
- boundary point /
- boundary edge /
- boundary loop

HTML全文

图 1 界点、界边、界环和等值面

Figure 1. Boundary point, boundary edge, boundary loop and iso-surface

下载: 全尺寸图片幻灯片

图 2 网顶点、网边点和网内点

Figure 2. Grid vertex point, grid edge point and grid unit point

下载: 全尺寸图片幻灯片

图 3 网顶点的相邻点

Figure 3. Adjacent points of grid vertex

下载: 全尺寸图片幻灯片

图 4 网边点的相邻点

Figure 4. Adjacent points of grid edge point

下载: 全尺寸图片幻灯片

图 5 网内点的相邻点

Figure 5. Adjacent points of grid unit point

下载: 全尺寸图片幻灯片

图 6 界点

Figure 6. Boundary point

下载: 全尺寸图片幻灯片

图 7 界点组

Figure 7. Boundary point group

下载: 全尺寸图片幻灯片

图 8 界边

Figure 8. Boundary edge

下载: 全尺寸图片幻灯片

图 9 界环

Figure 9. Boundary loop

下载: 全尺寸图片幻灯片

图 10 等值面

Figure 10. Iso-surface

下载: 全尺寸图片幻灯片

图 11 本文方法流程

Figure 11. Flow of the proposed method

下载: 全尺寸图片幻灯片

图 12 面采样过程

Figure 12. Surface sampling procedure

下载: 全尺寸图片幻灯片

图 13 边界边构造

Figure 13. Boundary edge construction

下载: 全尺寸图片幻灯片

图 14 内界环嵌套

Figure 14. Nesting of inner boundary loop

下载: 全尺寸图片幻灯片

图 15 面${s_i}$分割结果和优化结果（根据${C_1}$）

Figure 15. Surface segmentation results and optimization results for ${s_i}$ (according to ${C_1}$)

下载: 全尺寸图片幻灯片

图 16 面s_i分割结果和高斯曲率色标（根据C₂）

Figure 16. Surface segmentation results and Gaussian curvature color scale for s_i (according to C₂)

下载: 全尺寸图片幻灯片

图 17 面${s_{12}}$分割结果

Figure 17. Surface segmentation result for ${s_{12}}$

下载: 全尺寸图片幻灯片

表 1 基础边线关系示意图及判断方法

Table 1. Judgment method of basic edge-line relationship

基础边线关系	示意图	判断方法
分离		① ${m_1} = 1$，${m_2} = 1$ ② $x = 1 \wedge y = 0 \wedge {\textit{z}} = n + 1 \wedge w = 0$ ③ ${h_1} = n + 1 \wedge {h_2} = 0$
相交		① ${m_1} = 1$，${m_2} = 1$ ② $ y = 0 \wedge w = 0 \vee $ $ y \ne 0 \wedge w \ne 0 \wedge w - y \leqslant 1 \vee $ $ y \ne 0 \wedge w \ne 0 \wedge w - y \geqslant 2 \wedge {h_2} = 2 $
单搭接		① 当${m_1} \gt 1$，${m_2} = 1$时， $x = 2 \wedge y = 1 \wedge {\textit{z}} = n + 1 \wedge w = 1$ ② 当${m_1} = 1$，${m_2} \gt 1$时， $x = 1 \wedge y = n + 1 \wedge {\textit{z}} = n \wedge w = n + 1$ ③ ${h_1} = n \wedge {h_2} = 1$
双搭接		① ${m_1} \gt 1$，${m_2} \gt 1$ ② $x = 2 \wedge y = 1 \wedge {\textit{z}} = n \wedge w = n + 1$ ③ ${h_1} = n - 1 \wedge {h_2} = 2$
部分重合		① 当${m_1} = 1$，${m_2} = 1$时， $\begin{gathered} y \ne 0 \wedge w \ne 0 \wedge w - y \geqslant 2 \wedge \\[-5pt] {h_2} = w - y + 1 \\ \end{gathered} $ ② 当${m_1} \gt 1$，${m_2} = 1$时， $ \begin{gathered} x \gt 2 \wedge y = 1 \wedge {\textit{z}} = n + 1 \wedge w \gt 1 \wedge \\[-5pt] x - w = 1 \\\end{gathered} $ ③ 当${m_1} = 1$，${m_2} \gt 1$时， $ \begin{gathered} x = 1 \wedge y \lt n + 1 \wedge {\textit{z}} \lt n \wedge w = n + 1 \wedge \\[-5pt] y - {\textit{z}} = 1 \\ \end{gathered} $
包含重合		① ${m_1} \gt 1$，${m_2} \gt 1$ ② $x = 0 \wedge y = 1 \wedge {\textit{z}} = 0 \wedge w = n + 1$ ③ ${h_1} = 0 \wedge {h_2} = n + 1$

下载: 导出CSV

表 2 混合边线关系

Table 2. Mixed edge-line relationship

混合边线关系	示意图
相交与单搭接混合
相交与双搭接混合
相交与部分重合混合
单搭接与部分重合混合
双搭接与部分重合混合

下载: 导出CSV

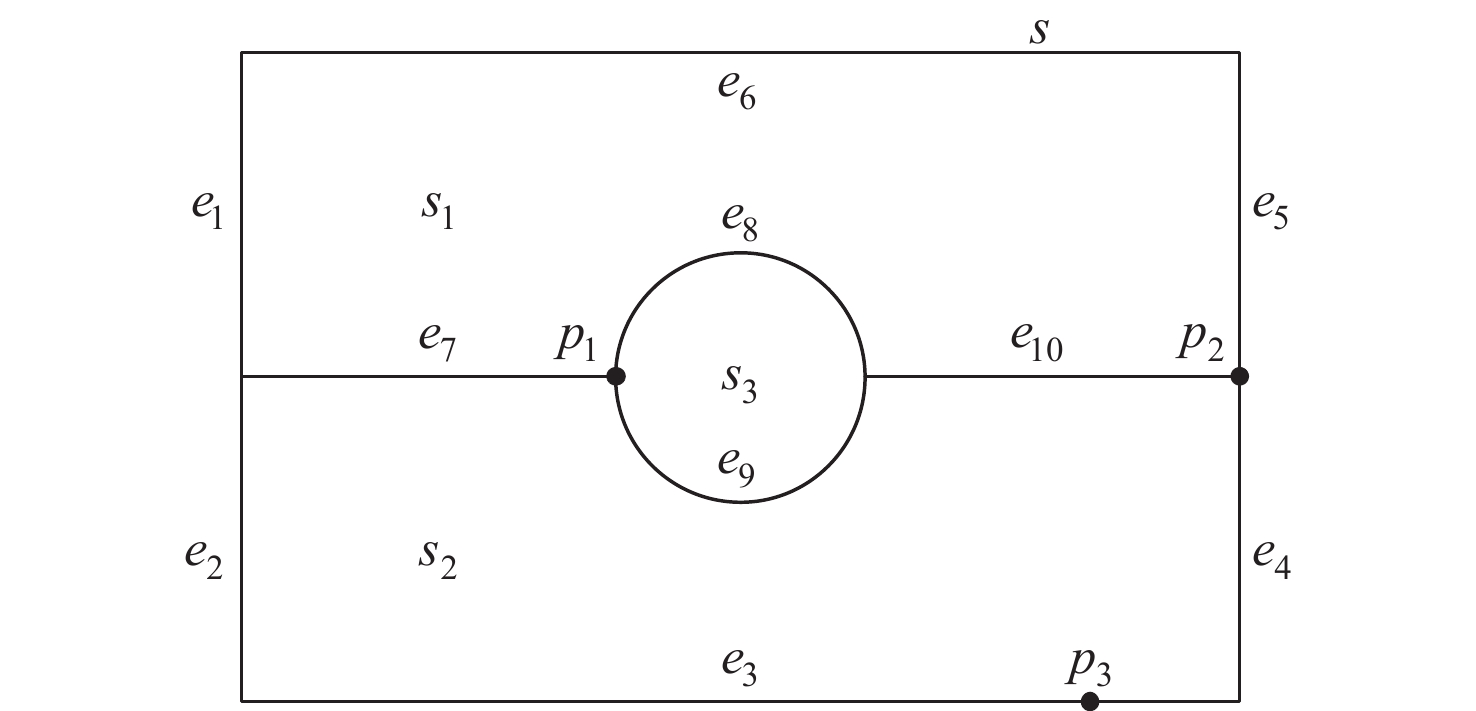
表 3 边界关系

Table 3. Edge-boundary relationship

边界关系		示意图
分离
端点搭接	单端点搭接
端点搭接	双端点搭接
边内搭接	单边内搭接
边内搭接	多边内搭接
混合搭接

下载: 导出CSV

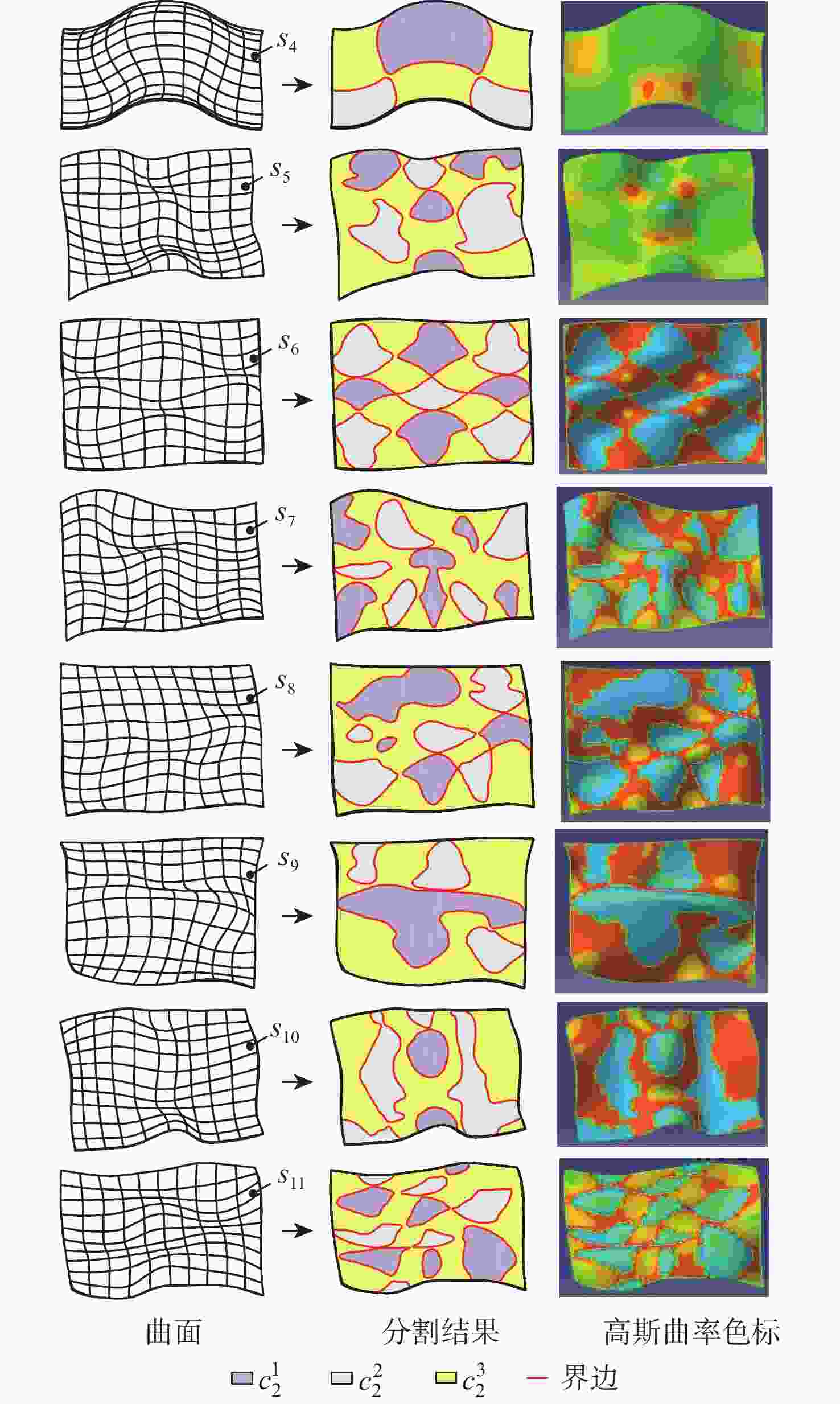
表 4 面s₄至s₁₁分割数据（根据C₂）

Table 4. Surface segmentation data for s₄ to s₁₁ (according to C₂)

曲面	$ N $	$ {\mathrm{Err}}/{\mathrm{m}}{{\mathrm{m}}}^{-1} $	$ T/{\mathrm{s}} $
$ {s}_{4} $	64	2.635×10⁻⁶	2.142
$ {s}_{5} $	261	2.609×10⁻⁶	8.602
$ {s}_{6} $	386	1.786×10⁻⁴	9.998
$ {s}_{7} $	314	5.847×10⁻⁶	6.760
$ {s}_{8} $	305	1.052×10⁻⁵	8.596
$ {s}_{9} $	232	7.690×10⁻⁶	7.637
$ {s}_{10} $	257	4.762×10⁻⁶	9.622
$ {s}_{11} $	330	3.919×10⁻⁶	10.265

下载: 导出CSV

表 5 面s_i分割数据对比（根据C₂）

Table 5. Surface segmentation data comparison for $ {s_{i}} $ (according to C₂)

曲面	方法	$N$	${\mathrm{Err}}/{\mathrm{m}}{{\mathrm{m}}^{ - 1}}$	$T/{\mathrm{s}}$
${s_4}$	文献[17]	88	2.306×10⁻⁷	3.267
${s_4}$	本文方法	64	2.635×10⁻⁶	2.142
${s_5}$	文献[17]	344	2.335×10⁻⁶	13.763
${s_5}$	本文方法	261	2.609×10⁻⁶	8.602
${s_6}$	文献[17]	502	1.307×10⁻⁴	17.662
${s_6}$	本文方法	386	1.786×10⁻⁴	9.998

下载: 导出CSV

表 6 面$ {s_{12}} $分割数据对比

Table 6. Surface segmentation data comparison for $ {s_{12}} $

方法	$\tau /{\mathrm{mm}}$	$N$	$T/{\mathrm{s}}$
文献[13]	6	13	1.07
	4	17	1.22
	2	33	1.75
	1	65	2.62
文献[17]	6	14	1.18
	4	19	1.48
	2	35	2.26
	1	67	3.75
本文方法	6	12	1.64
	4	16	2.48
	2	32	6.07
	1	64	16.79

下载: 导出CSV

参考文献(17)

[1]	SUNIL V B, PANDE S S. Automatic recognition of features from freeform surface CAD models[J]. Computer-Aided Design, 2008, 40(4): 502-517. doi: 10.1016/j.cad.2008.01.006
[2]	WANG J, WANG Z G, ZHU W D, et al. Recognition of freeform surface machining features[J]. Journal of Computing and Information Science in Engineering, 2010, 10(4): 041006. doi: 10.1115/1.3527075
[3]	WANG J, YU Z Y. Geometric decomposition of 3D surface meshes using Morse theory and region growing[J]. The International Journal of Advanced Manufacturing Technology, 2011, 56(9): 1091-1103.
[4]	王洪申, 张树生, 白晓亮, 等. 基于区域分割的三维自由曲面相似性评价算法[J]. 计算机辅助设计与图形学学报, 2011, 23(2): 305-313. WANG H S, ZHANG S S, BAI X L, et al. 3D freeform surface similarity assessment algorithm based on region segmentation[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(2): 305-313(in Chinese).
[5]	林俊锋, 黄常标, 祁杨停. 复杂三角网格模型分治加工刀具轨迹生成[J]. 计算机辅助设计与图形学学报, 2015, 27(2): 362-370. LIN J F, HUANG C B, QI Y T. Tool path generation of partition machining for complex triangular mesh model[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(2): 362-370(in Chinese).
[6]	CHEN Z C, DONG Z M, VICKERS G W. Automated surface subdivision and tool path generation for 31212-axis CNC machining of sculptured parts[J]. Computers in Industry, 2003, 50(3): 319-331. doi: 10.1016/S0166-3615(03)00019-8
[7]	LIU X, LI Y G, LI Q. A region-based 3+2-axis machining toolpath generation method for freeform surface[J]. The International Journal of Advanced Manufacturing Technology, 2018, 97(1): 1149-1163.
[8]	XU K, LI Y G. Region based five-axis tool path generation for freeform surface machining via image representation[J]. Robotics and Computer-Integrated Manufacturing, 2019, 57: 230-240. doi: 10.1016/j.rcim.2018.12.006
[9]	PARK S C, CHOI B K. Boundary extraction algorithm for cutting area detection[J]. Computer-Aided Design, 2001, 33(8): 571-579.
[10]	YANG J Z, WANG Q F, HUANG Z D, et al. Cutting area extraction from a Z-map model[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(9): 1010-1016.
[11]	VAN TUONG N, POKORNY P. A practical approach for partitioning free-form surfaces[J]. International Journal of Computer Integrated Manufacturing, 2010, 23(11): 992-1001. doi: 10.1080/0951192X.2010.506656
[12]	GUPTA R K, GURUMOORTHY B. Automatic extraction of free-form surface features(FFSFs)[J]. Computer-Aided Design, 2012, 44(2): 99-112. doi: 10.1016/j.cad.2011.09.012
[13]	陈俊, 郑国磊, 罗智波. 面向数控加工的面等值自动分片方法[J]. 计算机辅助设计与图形学学报, 2015, 27(5): 924-929. CHEN J, ZHENG G L, LUO Z B. A method of automatic iso-surface segmentation for NC machining[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(5): 924-929(in Chinese).
[14]	LIU X, LI Y G, MA S B, et al. A tool path generation method for freeform surface machining by introducing the tensor property of machining strip width[J]. Computer-Aided Design, 2015, 66: 1-13. doi: 10.1016/j.cad.2015.03.003
[15]	KUMAZAWA G H, FENG H Y, BARAKCHI FARD M J. Preferred feed direction field: a new tool path generation method for efficient sculptured surface machining[J]. Computer-Aided Design, 2015, 67: 1-12.
[16]	HUANG R, JIANG J F, HE K J, et al. An effective freeform surface retrieval approach for potential machining process reuse[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(9): 4341-4358.
[17]	胡靖尘, 郑国磊. CAD曲面等值分割方法[J]. 计算机辅助设计与图形学学报, 2021, 33(1): 153-160. HU J C, ZHENG G L. CAD surface iso-segmentation[J]. Journal of Computer-Aided Design & Computer Graphics, 2021, 33(1): 153-160(in Chinese).