改进的表贴式PMSM快速超扭曲滑模位置跟踪控制

谭草; 郝明基; 陆佳瑜; 韦青坤; 任浩鑫

doi:10.13700/j.bh.1001-5965.2023.0612

改进的表贴式PMSM快速超扭曲滑模位置跟踪控制

doi: 10.13700/j.bh.1001-5965.2023.0612

谭草¹,
郝明基^{1, 2},
陆佳瑜^1, ,,
韦青坤¹,
任浩鑫¹

1.
山东理工大学交通与车辆工程学院，淄博 255000
2.
山东交通职业学院车辆工程学院，潍坊 261000

基金项目:

国家自然科学基金(52305265)；山东省自然科学基金(ZR2023ME178)；山东省科技中小企业创新能力提升项目(2023TSGC0404)；山东省高等学校“青创团队计划”(2022KJ232)

详细信息

通讯作者:
E-mail：lujiayu@sdut.edu.cn

中图分类号: TM341
计量
- 文章访问数: 251
- HTML全文浏览量: 98
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-26
- 录用日期: 2023-11-03
- 网络出版日期: 2023-11-20
- 整期出版日期: 2025-11-25

Improved surface PMSM fast super-twisted sliding mode position tracking control

TAN Cao¹,
HAO Mingji^{1, 2},
LU Jiayu^{1
, ,},
WEI Qingkun¹,
REN Haoxin¹

1.
School of Transportation and Vehicle Engineering，Shandong University of Technology，Zibo 255000，China
2.
School of Vehicle Engineering，Shandong Transport Vocational College，Weifang 261000，China

Funds:

National Natural Science Foundation of China (52305265); Shandong Provincial Natural Science Foundation (ZR2023ME178); Shandong Province Science and Technology Small and Medium Enterprises Innovation Ability Enhancement Project (2023TSGC0404); Shandong Province Higher Education “Youth Innovation Team Plan” (2022KJ232)

More Information

Corresponding author: E-mail：lujiayu@sdut.edu.cn

摘要

摘要:
针对表贴式永磁同步电机(PMSM)伺服系统的位置跟踪控制问题，提出一种基于改进快速超扭曲算法(STA)的非奇异快速终端滑模控制(NFTSMC)和自适应扩展滑模扰动观测器(AESMDO)的复合控制策略。建立含扰动的表贴式PMSM数学模型；为避免奇异性和抖振现象，设计快速超扭曲非奇异快速终端滑模控制器，将改进的快速STA作为趋近阶段的切换控制律，相比于传统的二阶滑模有更快的趋近速度。针对电机容易受到参数变化及外界干扰影响的特点，为提高系统抗干扰能力，设计AESMDO来估计扰动，并以前馈方式进行补偿，通过Lyapunov定理证明系统的稳定性及在有限时间内收敛，并进行了试验验证。结果表明：设计的控制器实现了对系统给定值有效的跟踪控制，有效消除了抖振现象，提高了系统的鲁棒性。
- 表贴式永磁同步电机 /
- 非奇异快速终端滑模 /
- 超扭曲算法 /
- 自适应扩展滑模扰动观测器 /
- 位置跟踪
Abstract:
To solve the problem of position tracking control of the surface permanent magnet synchronous motor (PMSM) servo system, a compound control strategy based on non-singular fast terminal sliding mode control (NFTSMC) using an improved fast super-twisting algorithm (STA) and adaptive extend sliding mode disturbance observer (AESMDO) is proposed. Firstly, the mathematical model of surface PMSM with disturbance is established. Secondly, a fast super-twisting nonsingular fast terminal sliding mode controller is designed to prevent singularity and chattering. The improved fast STA is used as the switching control law of the approach phase, which has a faster approach speed than the traditional second-order sliding mode. In order to improve the system’s ability to resist disturbance, finally, an AESMDO is designed to estimate the disturbance and compensate by the feedforward method. The stability and convergence of the system in finite time are proved by Lyapunov’s theorem, and the experiment is carried out. The outcomes demonstrate how well the developed controller can monitor and regulate the system’s specified value, effectively remove the buffeting phenomenon, and increase the system’s resilience.
- surface permanent magnet synchronous motor /
- non-singular fast terminal sliding mode /
- super-twisting algorithm /
- adaptive extend sliding mode disturbance observer /
- position tracking

HTML全文

图 1 基于复合控制策略的表贴式PMSM伺服系统结构

Figure 1. Structure of surface PMSM servo system based on the composite control strategy

下载: 全尺寸图片幻灯片

图 2 本文复合控制策略位置环框图

Figure 2. Block diagram of the position loop of the composite control strategy in this paper

下载: 全尺寸图片幻灯片

图 3 表贴式PMSM试验平台

Figure 3. Surface PMSM experimental platform

下载: 全尺寸图片幻灯片

图 4 AESMDO对扰动的影响

Figure 4. The effect of AESMDO to the disturbance

下载: 全尺寸图片幻灯片

图 5 改进前后q轴参考电流输出对比

Figure 5. Comparison of q-axis reference current output before and after improvement

下载: 全尺寸图片幻灯片

图 6 正弦跟踪试验结果

Figure 6. Tracking experimental results of sine

下载: 全尺寸图片幻灯片

图 7 阶跃跟踪试验结果

Figure 7. Tracking experimental results of step

下载: 全尺寸图片幻灯片

图 8 白噪声下方波跟踪结果

Figure 8. Square wave tracking results in white noise

下载: 全尺寸图片幻灯片

图 9 给定负载下三角目标跟踪结果

Figure 9. Results of triangular tracking results for a given load

下载: 全尺寸图片幻灯片

图 10 转动惯量变化和磁链变化时的跟踪结果

Figure 10. Tracking results of changing the inertia and the magnetic linkage

下载: 全尺寸图片幻灯片

表 1 表贴式PMSM参数

Table 1. Surface PMSM parameters

参数	数值
输出额定功率/W	400
额定转速/(r·min⁻¹)	3000
额定电压/V	60
额定电流/A	8.5
极对数	4
定子电阻/$ \Omega $	0.19
定子电感/$ {\rm H} $	0.00065
转子磁链/$ {\text{Wb}} $	0.018
转动惯量/($ {\text{kg}} \cdot {{\text{m}}^{\text{2}}} $)	0.0000342
阻尼系数/(N·s·m⁻¹)	0.0001

下载: 导出CSV

表 2 位置跟踪误差分析数据

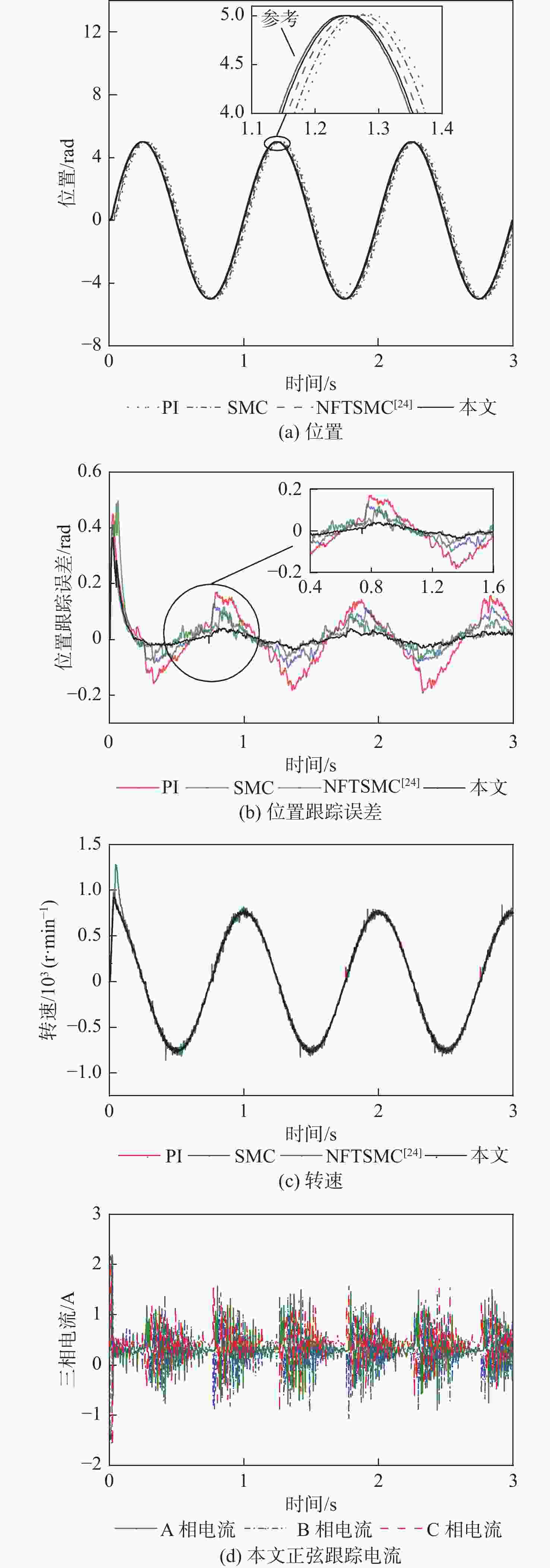
Table 2. Position tracking error analysis data rad

信号类型	控制方法	平均误差	最大误差	标准差
正弦信号	PI	0.0066	0.4500	0.1051
	SMC	0.0128	0.4050	0.0697
	NFTSMC^[24]	0.0207	0.4680	0.0723
	本文	0.0103	0.3640	0.0453
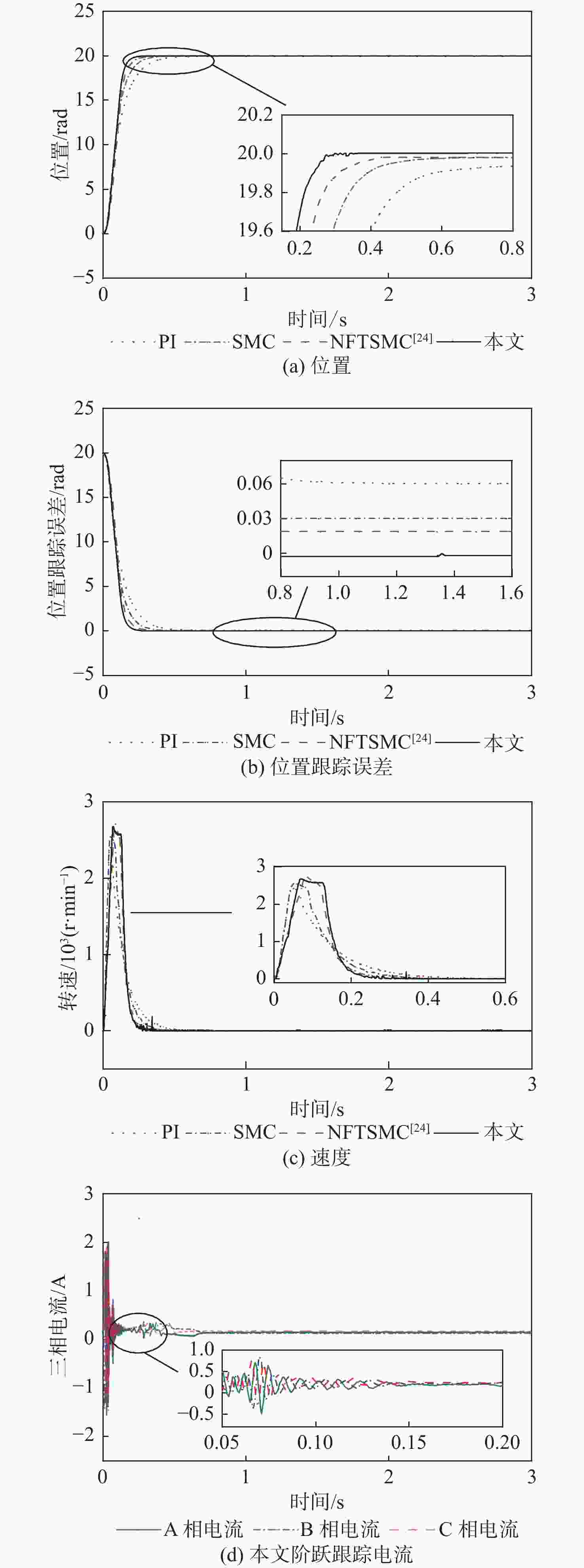
阶跃信号	PI	0.6599	0.0600	2.6350
	SMC	0.5322	0.0350	2.5289
	NFTSMC^[24]	0.5134	0.0150	2.6560
	本文	0.4413	0.0002	2.5272
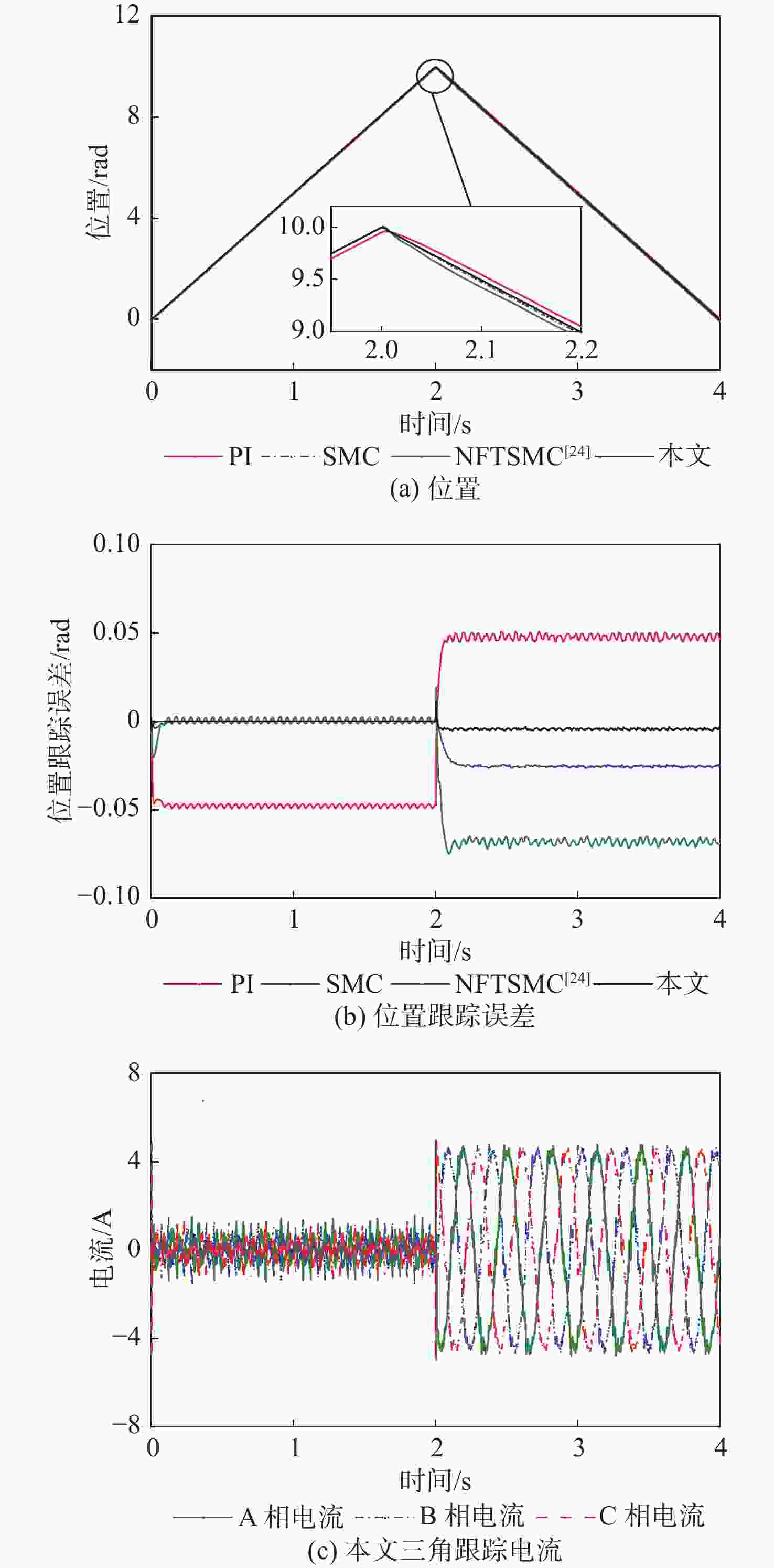
方波信号	PI	0.0010	0.0025	1.9167
	SMC	−0.0004	0.0005	1.8934
	NFTSMC^[24]	0.0004	0.0038	1.7305
	本文	0.0006	0.0001	1.7242
三角信号	PI	0.0002	0.0507	0.0475
	SMC	0.0122	0.0264	0.0125
	NFTSMC^[24]	0.0336	0.0748	0.0340
	本文	0.0021	0.0005	0.0022

下载: 导出CSV

参考文献(24)

[1]	QIU Z Z, CHEN Y, LIU X, et al. Evaluation and comparison of sideband harmonics and acoustic responses with continuous and discontinuous PWM strategies in permanent magnet synchronous motor for electric vehicles[J]. International Journal of Hydromechatronics, 2022, 5(2): 109. doi: 10.1504/IJHM.2022.123132
[2]	黄文卿, 张幽彤, 张兴春. 车用永磁同步电机功率闭环扭矩控制方法[J]. 北京理工大学学报, 2015, 35(3): 246-250. HUANG W Q, ZHANG Y T, ZHANG X C. Research on power closed-loop torque control strategy of PMSM in HEV application[J]. Transactions of Beijing Institute of Technology, 2015, 35(3): 246-250(in Chinese).
[3]	张卓然, 陆嘉伟, 张伟秋, 等. 飞机电推进系统高效能电机及其驱动控制技术[J]. 中国电机工程学报, 2024, 44(16): 6610-6632. ZHANG Z R, LU J W, ZHANG W Q, et al. High-performance electric machine and drive technologies for aircraft electric propulsion systems[J]. Proceedings of the CSEE, 2024, 44(16): 6610-6632(in Chinese).
[4]	李兵强, 吴春, 林辉. 基于参考输入学习的永磁同步电机高精度位置伺服系统[J]. 中国电机工程学报, 2012, 32(3): 96-102. LI B Q, WU C, LIN H. A high-precision position servo system of permanent magnet synchronous motors with reference input iterative learning[J]. Proceedings of the CSEE, 2012, 32(3): 96-102(in Chinese).
[5]	许叙遥, 林辉. 基于动态滑模控制的永磁同步电机位置速度一体化设计[J]. 电工技术学报, 2014, 29(5): 77-83. XU X Y, LIN H. Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 77-83(in Chinese).
[6]	谭草, 鲁应涛, 葛文庆, 等. 直驱式永磁直线电机深度模糊滑模-自抗扰控制[J]. 西安交通大学学报, 2023, 57(1): 185-194. TAN C, LU Y T, GE W Q, et al. Depth fuzzy sliding-mode active disturbance rejection control method of permanent magnet linear motor for direct drive system[J]. Journal of Xi’an Jiaotong University, 2023, 57(1): 185-194(in Chinese).
[7]	QI L, SHI H B. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control[J]. Neurocomputing, 2013, 115: 23-30. doi: 10.1016/j.neucom.2012.11.018
[8]	谭草, 黎德祥, 葛文庆, 等. 改进LuGre模型的电磁直线执行器自适应鲁棒控制[J]. 电机与控制学报, 2022, 26(10): 130-138. TAN C, LI D X, GE W Q, et al. Adaptive robust control for electromagnetic linear actuator with improved LuGre model[J]. Electric Machines and Control, 2022, 26(10): 130-138(in Chinese).
[9]	TANG Y. Terminal sliding mode control for rigid robots[J]. Automatica, 1998, 34(1): 51-56. doi: 10.1016/S0005-1098(97)00174-X
[10]	MOBAYEN S. Fast terminal sliding mode controller design for nonlinear second-order systems with time-varying uncertainties[J]. Complexity, 2015, 21(2): 239-244. doi: 10.1002/cplx.21600
[11]	CHEN S Y, LIU W, HUANG H X. Nonsingular fast terminal sliding mode tracking control for a class of uncertain nonlinear systems[J]. Journal of Control Science and Engineering, 2019, 2019(Pt. 1): 8146901.1-8146901.17.
[12]	潘菲, 朱宏玉. 航天器非奇异自适应终端滑模姿轨联合控制[J]. 北京航空航天大学学报, 2020, 46(7): 1354-1362. PAN F, ZHU H Y. Spacecraft non-singular adaptive terminal sliding mode attitude-orbit coupling control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(7): 1354-1362(in Chinese).
[13]	谭草, 李波, 于鹏, 等. 电磁直驱静液作动器多学科建模与优化[J]. 北京理工大学学报, 2022, 42(10): 1080-1088. TAN C, LI B, YU P, et al. Multidisciplinary modeling and optimization of direct-driving electro-hydrostatic actuator[J]. Transactions of Beijing Institute of Technology, 2022, 42(10): 1080-1088(in Chinese).
[14]	赵国荣, 李晓宝, 刘帅, 等. 自适应非奇异快速终端滑模固定时间收敛制导律[J]. 北京航空航天大学学报, 2019, 45(6): 1059-1070. ZHAO G R, LI X B, LIU S, et al. Adaptive nonsingular fast terminal sliding mode guidance law with fixed-time convergence[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(6): 1059-1070(in Chinese).
[15]	XIU C B, GUO P H. Global terminal sliding mode control with the quick reaching law and its application[J]. IEEE Access, 2018, 6: 49793-49800. doi: 10.1109/ACCESS.2018.2868785
[16]	BARTOLINI G, LEVANT A, PISANO A, et al. Adaptive second-order sliding mode control with uncertainty compensation[J]. International Journal of Control, 2016, 89(9): 1747-1758. doi: 10.1080/00207179.2016.1142616
[17]	刘春光, 徐浩轩, 高强, 等. 混合动力车辆机组的准滑动模态速度控制策略[J]. 计算机仿真, 2020, 37(12): 12-15. doi: 10.3969/j.issn.1006-9348.2020.12.003 LIU C G, XU H X, GAO Q, et al. Quasi-sliding mode speed control strategy for hybrid electric vehicle units[J]. Computer Simulation, 2020, 37(12): 12-15(in Chinese). doi: 10.3969/j.issn.1006-9348.2020.12.003
[18]	涂宇, 王怡, 吴志海, 等. 基于超扭曲算法的解耦非奇异快速终端滑模[J]. 控制工程, 2020, 27(2): 271-277. TU Y, WANG Y, WU Z H, et al. Decoupled nonsingular fast terminal sliding mode control based on super twisted algorithm[J]. Control Engineering of China, 2020, 27(2): 271-277(in Chinese).
[19]	张庆超, 马瑞卿, 皇甫宜耿, 等. 电机转速环节Super-Twisting算法二阶滑模控制律设计与研究[J]. 西北工业大学学报, 2016, 34(4): 669-676. ZHANG Q C, MA R Q, HUANGFU Y G, et al. Second-order sliding mode control based on Super-Twisting algorithm for the speed outer loop of motors[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 669-676(in Chinese).
[20]	许德智, 黄泊珉, 杨玮林. 神经网络自适应的永磁直线同步电机超扭曲终端滑模控制[J]. 电力系统保护与控制, 2021, 49(13): 64-71. XU D Z, HUANG B M, YANG W L. Neural network adaptive super twist terminal sliding mode control for a permanent magnet linear synchronous motor[J]. Power System Protection and Control, 2021, 49(13): 64-71(in Chinese).
[21]	WANG Y, YU H T, FENG N J, et al. Non-cascade backstepping sliding mode control with three-order extended state observer for PMSM drive[J]. IET Power Electronics, 2020, 13(2): 307-316. doi: 10.1049/iet-pel.2019.0819
[22]	武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512. WU Z T, LI S, CHENG W S. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512(in Chinese).
[23]	付建斌, 康恺. 非奇异快速终端滑模的分数阶迭代学习控制策略研究[J]. 制造业自动化, 2022, 44(11): 119-122. FU J B, KANG K. Fractional order iterative iearning control strategy of nonsingular fast terminal sliding mode[J]. Manufacturing Automation, 2022, 44(11): 119-122(in Chinese).
[24]	张智鑫, 刘旭东. 基于ESO的永磁同步电机伺服系统快速终端滑模控制[J]. 控制理论与应用, 2023, 40(7): 1233-1242. ZHANG Z X, LIU X D. Fast terminal sliding mode control of permanent magnet synchronous motor servo system with ESO[J]. Control Theory & Applications, 2023, 40(7): 1233-1242(in Chinese).