融合多策略改进的侏儒猫鼬算法

于明洋; 李婷; 许静

doi:10.13700/j.bh.1001-5965.2023.0613

融合多策略改进的侏儒猫鼬算法

doi: 10.13700/j.bh.1001-5965.2023.0613

于明洋¹,
李婷^{2, 3, ,},
许静¹

1.
南开大学人工智能学院，天津 300350
2.
南开大学计算机学院，天津 300350
3.
天津津航技术物理研究所，天津 300350

基金项目:

天津市自然科学基金(21JCYBJC00110)

详细信息

通讯作者:
E-mail：t24725@126.com

中图分类号: V221⁺.3；TB553
计量
- 文章访问数: 35
- HTML全文浏览量: 7
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-26
- 录用日期: 2023-12-15
- 网络出版日期: 2024-01-19
- 整期出版日期: 2025-11-25

Enhanced dwarf mongoose optimization algorithm with multi-strategy fusion

YU Mingyang¹,
LI Ting^{2, 3
, ,},
XU Jing¹

1.
College of Artificial Intelligence，Nankai University，Tianjin 300350，China
2.
College of Computer Science，Nankai University，Tianjin 300350，China
3.
Tianjin Jinhang Institute of Technical Physics，Tianjin 300350，China

Funds:

Natural Science Foundation of Tianjin Municipality (21JCYBJC00110)

More Information

Corresponding author: E-mail：t24725@126.com

摘要

摘要:
针对侏儒猫鼬优化算法(DMO)易陷入局部最优和收敛效率低的问题，提出一种多策略融合的增强型侏儒猫鼬算法(EDMO)。该算法引入随机反向学习策略增强猫鼬种群的多样性和质量，以增强其全局搜索能力和提高收敛速度。同时，采用自适应的方式更新保姆交换系数，以平衡全局探索与局部开发的需求。在迭代的后期，算法利用黏菌觅食行为，在局部与全局最优解之间进行优化。通过对CEC2017测试函数集的求解，对不同的算法进行比较。结果表明：融合3种策略的EDMO在寻优精度、寻优速度和鲁棒性方面均优于对比的先进算法。通过对无人机三维路径规划的实验验证，EDMO在局部搜索方面表现优于原始DMO算法，同时生成的飞行路径也更为稳定。
- 侏儒猫鼬优化算法 /
- 多策略融合 /
- 随机反向学习 /
- 自适应 /
- 黏菌觅食行为 /
- 三维路径规划
Abstract:
The enhanced multi-strategy dwarf mongoose optimization algorithm (EDMO) is a proposed solution to the dwarf mongoose optimization algorithm's (DMO) low convergence efficiency and susceptibility to local optima. This algorithm employs a random opposite learning strategy to amplify the diversity and quality of the mongoose population, bolstering its global search capability and enhancing convergence accuracy. Concurrently, an adaptive approach is deployed to update the babysitter exchange coefficient, striking a balance between global exploration and local exploitation. In the latter stages of iteration, the algorithm capitalizes on the foraging behavior of the slime mold, optimizing between local and global optimal solutions. By solving the CEC2017 test function set, different algorithms are compared. The findings demonstrate that in terms of optimization accuracy, optimization speed, and resilience, EDMO which combines the three strategies performs better than the sophisticated algorithms under comparison. Through the experimental verification of UAV three-dimensional path planning, the EDMO algorithm performs better than the original DMO algorithm in local search, and the flight path generated is more stable.
- dwarf mongoose optimization algorithm /
- multi-strategy fusion /
- random reverse learning /
- adaptive /
- fungal foraging behavior /
- three-dimensional path planning

HTML全文

图 1 非线性比例因子γ

Figure 1. Nonlinear scaling factor γ

下载: 全尺寸图片幻灯片

图 2 EDMO流程

Figure 2. Flow of EDMO

下载: 全尺寸图片幻灯片

图 3 α和f₁₄拟合曲线

Figure 3. Fitted curve with α and f₁₄

下载: 全尺寸图片幻灯片

图 4 收敛曲线对比

Figure 4. Convergence curves comparison

下载: 全尺寸图片幻灯片

图 5 三维威胁地图

Figure 5. Three-dimensional threat topographic map

下载: 全尺寸图片幻灯片

图 6 二维航迹规划（DMO）

Figure 6. Two-dimensional track plan （DMO）

下载: 全尺寸图片幻灯片

图 7 三维航迹规划（DMO）

Figure 7. Three-dimensional track plan （DMO）

下载: 全尺寸图片幻灯片

图 8 适应度变化曲线（DMO）

Figure 8. Fitness change curve （DMO）

下载: 全尺寸图片幻灯片

图 9 二维航迹规划（EDMO）

Figure 9. Two-dimensional track plan （EDMO）

下载: 全尺寸图片幻灯片

图 10 三维航迹规划（EDMO）

Figure 10. Three-dimensional track plan （EDMO）

下载: 全尺寸图片幻灯片

图 11 适应度变化曲线（EDMO）

Figure 11. Fitness change curve （EDMO）

下载: 全尺寸图片幻灯片

表 1 29个CEC2017测试函数

Table 1. 29 CEC2017 test functions

函数	函数名称	最优适应度值	函数	函数名称	最优适应度值
f₁	Shifted and Rotated Bent Cigar Function	100	f₁₇	Hybrid Function 6(N=4)	1700
f₃	Shifted and Rotated Zakharov Function	300	f₁₈	Hybrid Function 6(N=5)	1800
f₄	Shifted and Rotated Rosenbrock’s Function	400	f₁₉	Hybrid Function 6(N=5)	1900
f₅	Shifted and Rotated Rastrigin’s Function	500	f₂₀	Hybrid Function 6(N=6)	2000
f₆	Shifted and Rotated Expanded Scaffer’s F6 Function	600	f₂₁	Composition Function 1(N=3)	2100
f₇	Shifted and Rotated Lunacek Bi-Rastrigin Function	700	f₂₂	Composition Function 2(N=3)	2200
f₈	Shifted and Rotated Non-Continuous Rastrigin’s Function	800	f₂₃	Composition Function 3(N=4)	2300
f₉	Shifted and Rotated Lévy Function	900	f₂₄	Composition Function 4(N=4)	2400
f₁₀	Shifted and Rotated Schwefel’s Function	1000	f₂₅	Composition Function 5(N=5)	2500
f₁₁	Hybrid Function 1(N=3)	1100	f₂₆	Composition Function 6(N=5)	2600
f₁₂	Hybrid Function 2(N=3)	1200	f₂₇	Composition Function 7(N=6)	2700
f₁₃	Hybrid Function 3(N=3)	1300	f₂₈	Composition Function 8(N=6)	2800
f₁₄	Hybrid Function 4(N=4)	1400	f₂₉	Composition Function 9(N=3)	2900
f₁₅	Hybrid Function 5(N=4)	1500	f₃₀	Composition Function 10(N=3)	3000
f₁₆	Hybrid Function 5(N=4)	1600

下载: 导出CSV

表 2 消融实验结果γ值对比

Table 2. Comparison of ablation results of γ

函数	DMO^[10]	EDMO1	EDMO2	EDMO3	函数	DMO^[10]	EDMO1	EDMO2	EDMO3
f₁	0.00	0.32	0.72	0.03	f₁₇	0.84	0.95	0.96	0.88
f₃	0.51	0.52	0.92	0.31	f₁₈	0.02	0.78	0.77	0.32
f₄	0.83	0.85	0.88	0.88	f₁₉	0.39	0.53	0.78	0.48
f₅	0.88	0.92	0.94	0.88	f₂₀	0.88	0.95	0.94	0.91
f₆	0.98	0.97	0.98	1.00	f₂₁	0.99	0.98	0.98	0.95
f₇	0.84	0.93	0.88	0.87	f₂₂	0.57	0.68	1.04	0.77
f₈	0.95	0.96	0.97	0.90	f₂₃	0.97	0.98	0.97	0.97
f₉	0.33	0.51	0.49	0.67	f₂₄	1.00	0.96	1.01	0.98
f₁₀	0.54	0.61	0.52	0.55	f₂₅	0.98	0.98	0.99	0.99
f₁₁	1.05	1.12	1.11	1.12	f₂₆	0.79	0.81	0.77	0.72
f₁₂	0.39	0.65	0.46	0.43	f₂₇	0.93	0.99	0.99	0.98
f₁₃	0.31	0.41	0.45	0.55	f₂₈	0.92	0.96	0.97	0.99
f₁₄	2.14	8.33	0.13	0.04	f₂₉	0.83	0.91	0.89	0.91
f₁₅	0.12	0.21	0.23	0.24	f₃₀	0.06	0.43	0.21	0.43
f₁₆	0.83	0.88	0.88	0.79

下载: 导出CSV

表 3 CEC2017测试结果

Table 3. Test results for CEC 2017

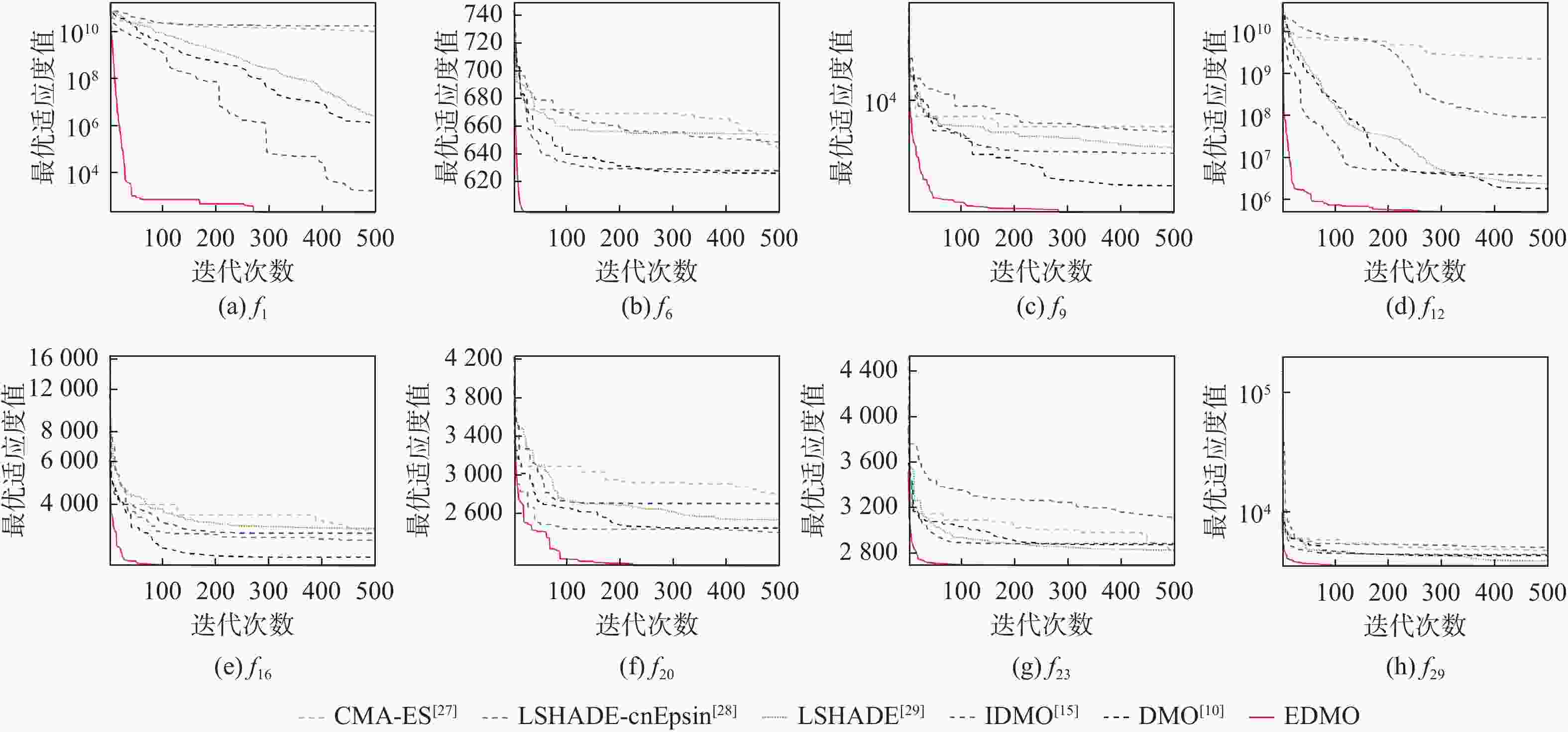
函数	CMA-ES^[27] 均值(标准差)	LSHADE_cnEpsin^[28] 均值(标准差)	LSHADE^[29] 均值(标准差)	DMO^[10] 均值(标准差)	IDMO^[15] 均值(标准差)	EDMO 均值(标准差)
f₁	1.32×10¹⁰(4.86×10⁹)/+	1.73×10¹⁰(5.77×10⁹)/+	2.38×10⁷(2.23×10⁷)/+	5.26×10⁶(1.13×10⁷)/+	1.98×10⁴(3.53×10⁴)/+	5.71×10²(7.02×10²)
f₃	6.35×10⁴(9.89×10³)/+	4.19×10⁴(1.02×10⁴)/+	6.44×10⁴(1.05×10⁴)/+	4.21×10⁴(9.81×10³)/+	1.62×10⁴(4.67×10³)/−	2.05×10⁴(2.01×10³)
f₄	1.37×10³(7.52×10²)/+	2.30×10³(1.59×10³)/+	5.35×10²(31.4)/+	5.20×10²(32.0)/+	5.21×10²(33.2)/+	4.39×10²(36.9)
f₅	7.12×10²(48.2)/+	7.73×10²(37.4)/+	6.83×10²(31.9)/+	6.31×10²(30.5)/+	6.54×10²(33.9)/+	5.57×10²(8.73)
f₆	6.38×10²(6.68)/+	6.62×10²(8.40)/+	6.43×10²(10.4)/+	6.22×10²(8.73)/+	6.33×10²(10.6)/+	6.02×10²(2.49×10^-13)
f₇	1.08×10³(61.4)/+	1.28×10³(54.7)/+	1.05×10³(52.4)/+	9.40×10²(59.5)/+	9.97×10²(67.7)/+	7.75×10²(6.11)
f₈	9.87×10²(39.5)/+	9.96×10²(26.0)/+	9.58×10²(25.7)/+	9.18×10²(19.6)/+	9.16×10²(24.7)/+	8.65×10²(10.6)
f₉	5.54×10³(1.40×10³)/+	5.86×10³(5.75×10²)/+	3.88×10³(4.76×10²)/+	3.45×10³(1.65×10³)/+	3.14×10³(8.49×10²)/+	1.14×10³(1.13×10²)
f₁₀	6.64×10³(1.43×10³)/+	5.34×10³(3.92×10²)/+	5.65×10³(2.85×10²)/+	5.73×10³(9.75×10²)/+	5.02×10³6.75×10²)/+	3.15×10³(2.67×10²)
f₁₁	3.75×10³(1.57×10³)/+	2.13×10³(6.78×10²)/=	1.23×10³(40.5)/=	1.32×10³(65.6)/=	1.27×10³(54.4)/=	1.35×10³(22.7)
f₁₂	9.57×10⁸(1.13×10⁹)/+	1.28×10⁹(1.26×10⁹)/+	1.63×10⁶(1.18×10⁶)/+	1.28×10⁶(9.25×10⁵)/+	8.78×10⁵(8.12×10⁵)/=	4.56×10⁵(2.58×10⁵)
f₁₃	4.76×10⁸(1.33×10⁹)/+	1.85×10⁷(5.16×10⁷)/=	1.75×10⁴(1.37×10⁴)/=	4.38×10⁴(2.86×10⁴)/+	2.08×10⁴(1.97×10⁴)/=	1.26×10⁴(6.56×10³)
f₁₄	1.18×10⁶(1.19×10⁶)/+	2.37×10⁴(2.42×10⁴)/−	2.76×10⁴(3.20×10⁴)/−	4.97×10⁴(5.13×10⁴)/−	1.50×10⁴(2.18×10⁴)/−	1.07×10⁵(6.23×10⁴)
f₁₅	1.58×10⁷(3.31×10⁷)/+	5.16×10⁴(4.74×10⁴)/+	5.66×10³(3.55×10³)/+	1.98×10⁴(2.24×10⁴)/+	9.73×10³(1.08×10⁴)/+	2.21×10³(1.63×10³)
f₁₆	2.95×10³(3.88×10²)/+	3.14×10³(3.98×10²)/+	2.88×10³(1.62×10²)/+	2.74×10³(4.02×10²)/+	2.76×10³(2.83×10²)/+	2.24×10³(1.35×10²)
f₁₇	2.34×10³(2.12×10²)/+	2.26×10³(1.84×10²)/+	2.03×10³(1.35×10²)/+	2.27×10³(1.65×10²)/+	2.38×10³(1.98×10²)/+	1.94×10³(88.2)
f₁₈	1.67×10⁶(1.94×10⁶)/+	4.97×10⁵(5.87×10⁵)/=	2.43×10⁵(1.94×10⁵)/=	2.07×10⁷(1.03×10⁸)/+	1.57×10⁵(1.55×10⁵)/=	1.46×10⁵(5.52×10⁴)
f₁₉	1.26×10⁷(3.22×10⁷)/+	1.63×10⁶(1.73×10⁶)/+	8.34×10³(7.38×10³)/+	9.64×10³(1.32×10⁴)/+	9.96×10³(1.13×10⁴)/+	3.61×10³(1.57×10³)
f₂₀	2.63×10³(1.89×10²)/+	2.52×10³(1.55×10²)/+	2.46×10³(1.05×10²)/+	2.60×10³(2.17×10²)/+	2.58×10³(2.28×10²)/+	2.25×10³(1.05×10²)
f₂₁	2.48×10³(41.2)/+	2.55×10³(73.6)/+	2.44×10³(25.7)/+	2.41×10³(22.6)/+	2.43×10³(30.2)/+	2.35×10³(44.4)
f₂₂	6.28×10³(2.67×10³)/+	5.76×10³(1.64×10³)/+	2.32×10³(31.0)/−	4.24×10³(2.81×10³)/+	4.92×10³(2.38×10³)/+	2.38×10³(39.4)
f₂₃	2.92×10³(63.4)/+	3.06×10³(91.5)/+	2.82×10³(32.4)/+	2.82×10³(75.3)/+	2.84×10³(45.5)/+	2.72×10³(11.1)
f₂₄	3.12×10³(71.5)/+	3.22×10³(67.6)/=	2.97×10³(34.5)/=	2.97×10³(77.8)/=	2.97×10³(57.5)/+	2.95×10³(25.3)
f₂₅	3.11×10³(1.25×10²)/+	3.35×10³(1.83×10²)/+	2.97×10³(24.7)/+	2.95×10³(22.8)/+	2.94×10³(18.4)/+	2.88×10³(0.879)
f₂₆	6.18×10³(6.04×10²)/+	7.22×10³(1.45×10³)/+	5.19×10³(1.70×10³)/+	4.72×10³(9.84×10²)/+	5.66×10³(1.47×10³)/+	3.71×10³(8.32×10²)
f₂₇	3.42×10³(79.2)/+	3.37×10³(65.6)/+	3.22×10³(16.4)/+	3.46×10³(24.2×10²)/+	3.27×10³(38.8)/+	3.23×10³(4.97)
f₂₈	3.92×10³(2.99×10²)/+	4.12×10³(4.07×10²)/+	3.33×10³(36.7)/+	3.56×10³(1.13×10³)/+	3.27×10³(25.6)/+	3.20×10³(10.5)
f₂₉	4.26×10³(2.46×10²)/+	4.58×10³(4.43×10²)/+	4.14×10³(2.23×10²)/+	4.22×10³(4.15×10²)/+	4.20×10³(2.81×10²)/+	3.52×10³(76.7)
f₃₀	4.06×10⁷(3.28×10⁷)/+	1.18×10⁷(8.86×10⁶)/+	2.94×10⁴(3.28×10⁴)/+	1.37×10⁵(2.82×10⁵)/+	2.13×10⁴(1.12×10⁴)/+	7.58×10³(1.22×10³)

下载: 导出CSV

表 4 风险区域二维坐标参数

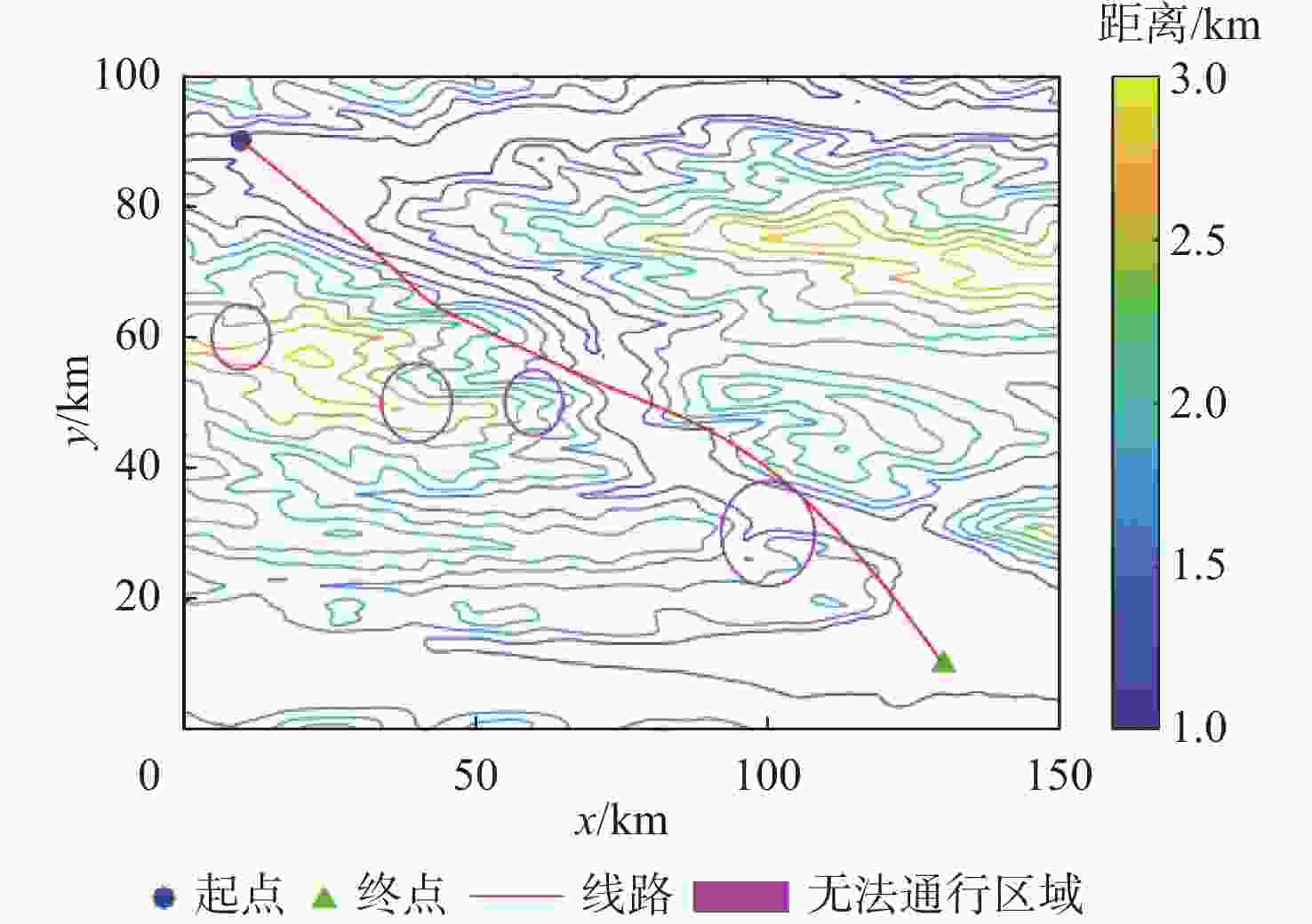
Table 4. 2D coordinate parameters of risk area

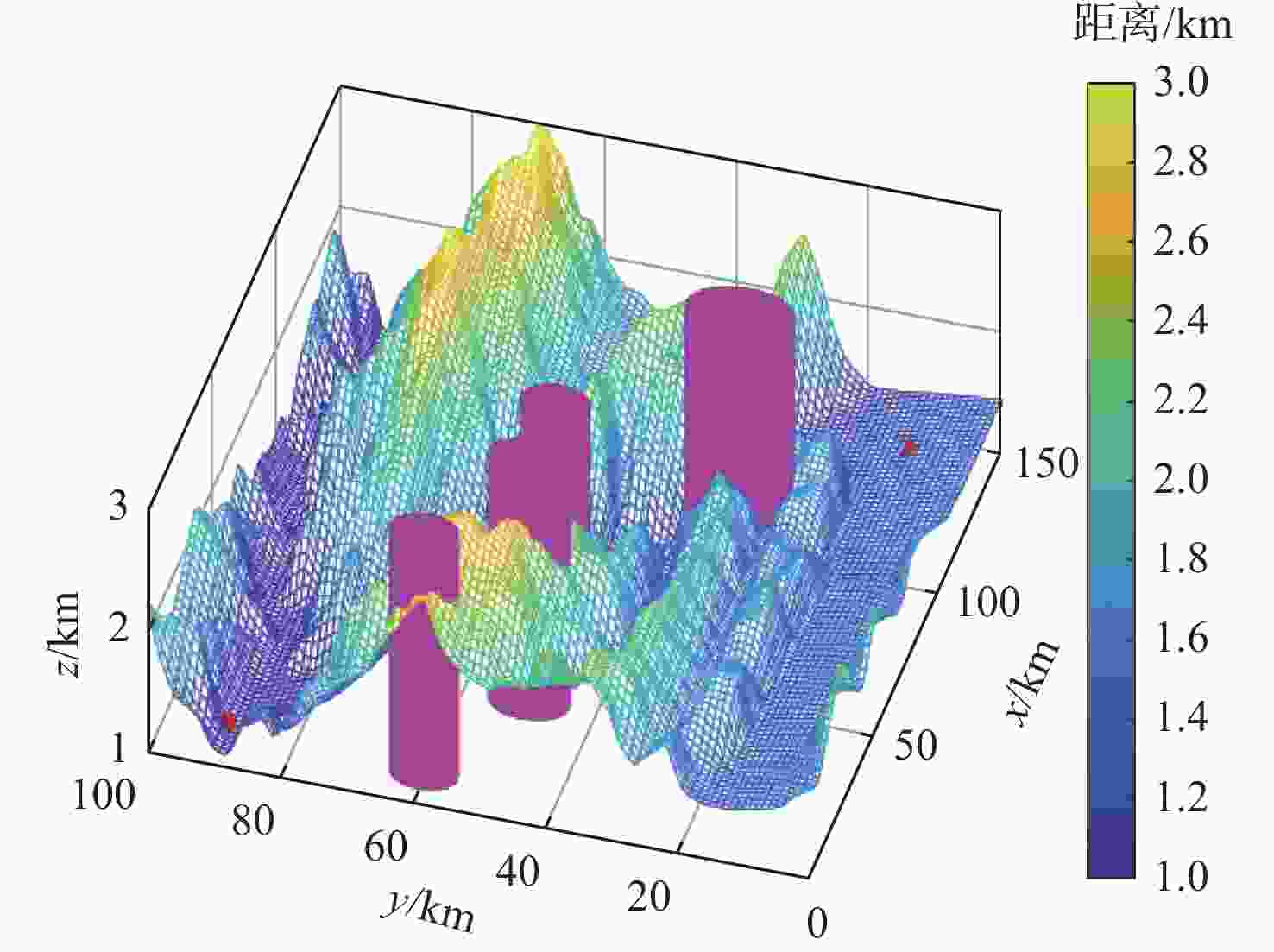
风险区域	中心点坐标/km	风险半径/km
1	(10,60)	5
2	(40,50)	6
3	(60,50)	5
4	(100,30)	8

下载: 导出CSV

表 5 无人机三维路径规划结果统计

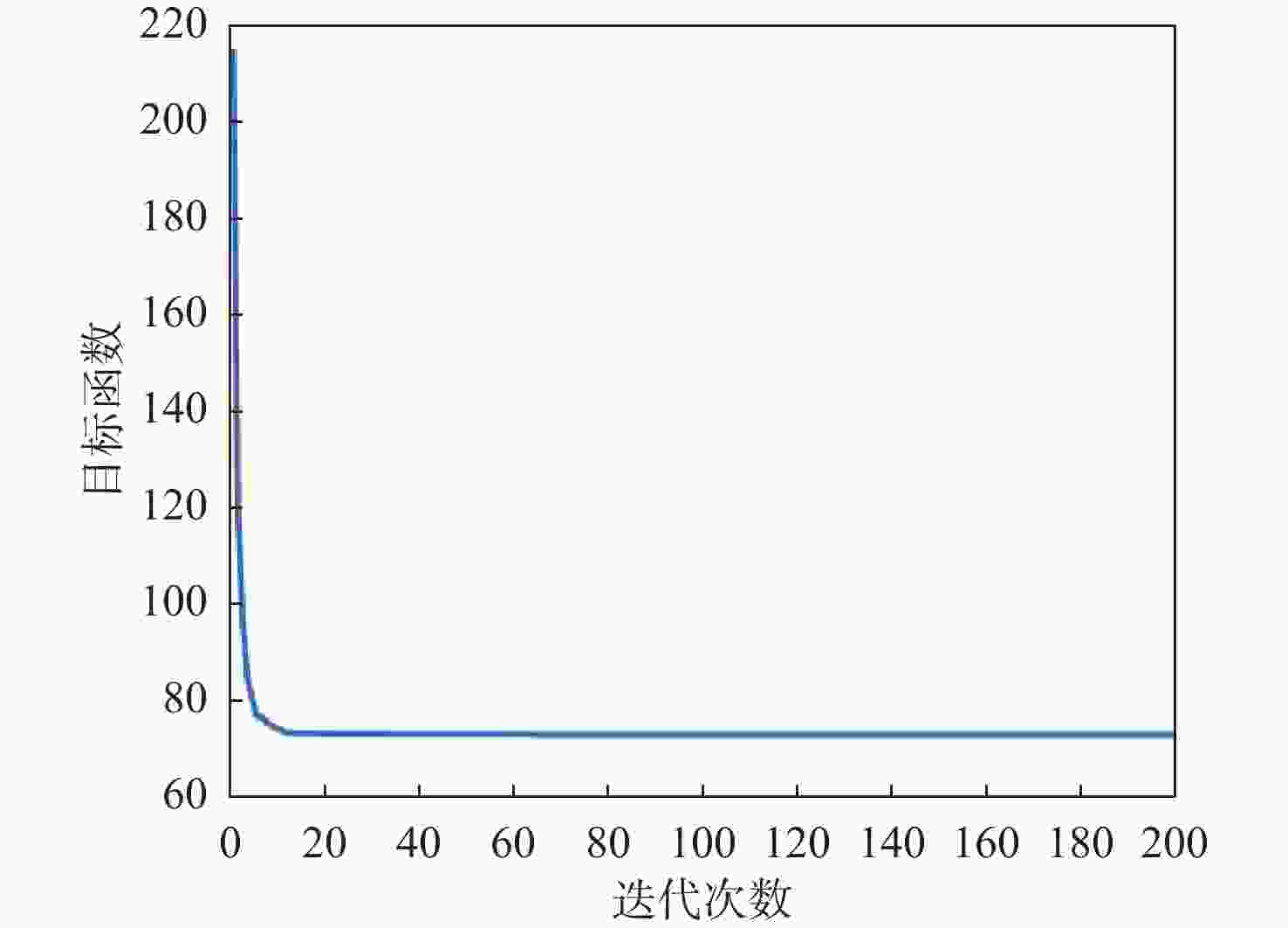
Table 5. Statistics of UAV three-dimensional path planning results

实验算法	最优代价	最差代价	平均代价	标准差	平均迭代次数	平均运行时间/ s
EDMO	72.92	72.97	72.96	0.03	124.53	37.41
DMO^[10]	72.96	73.07	73.01	0.08	117.60	39.77

下载: 导出CSV

参考文献(30)

[1]	宋立钦, 陈文杰, 陈伟海, 等. 基于混合策略的麻雀搜索算法改进及应用[J]. 北京航空航天大学学报, 2023, 49(8): 2187-2199. SONG L Q, CHEN W J, CHEN W H, et al. Improvement and application of hybrid strategy-based sparrow search algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(8): 2187-2199(in Chinese).
[2]	李全耀, 沈艳霞. 一种基于教与学的混合灰狼优化算法[J]. 控制与决策, 2022, 37(12): 3190-3196. LI Q Y, SHEN Y X. A hybrid gray wolf optimization algorithm based on the teaching-learning optimization[J]. Control and Decision, 2022, 37(12): 3190-3196(in Chinese).
[3]	MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. doi: 10.1016/j.advengsoft.2017.07.002
[4]	HASHIM F A, HUSSIEN A G. Snake Optimizer: a novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems, 2022, 242: 108320. doi: 10.1016/j.knosys.2022.108320
[5]	JIA H M, PENG X X, LANG C B. Remora optimization algorithm[J]. Expert Systems with Applications, 2021, 185: 115665. doi: 10.1016/j.eswa.2021.115665
[6]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[7]	ABD ELAZIZ M, LU S F, HE S B. A multi-leader whale optimization algorithm for global optimization and image segmentation[J]. Expert Systems with Applications, 2021, 175: 114841. doi: 10.1016/j.eswa.2021.114841
[8]	ZHANG L, ZHANG Y J, LI Y F. Mobile robot path planning based on improved localized particle swarm optimization[J]. IEEE Sensors Journal, 2021, 21(5): 6962-6972. doi: 10.1109/JSEN.2020.3039275
[9]	柴岩, 朱玉, 任生. 多策略协同的改进鲸鱼优化算法[J]. 计算机工程与科学, 2023, 45(7): 1308-1319. CHAI Y, ZHU Y, REN S. An improved whale optimization algorithm based on multi-strategy coordination[J]. Computer Engineering & Science, 2023, 45(7): 1308-1319(in Chinese).
[10]	AGUSHAKA J O, EZUGWU A E, ABUALIGAH L. Dwarf mongoose optimization algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 391: 114570. doi: 10.1016/j.cma.2022.114570
[11]	ALDOSARI F, ABUALIGAH L, ALMOTAIRI K H. A normal distributed dwarf mongoose optimization algorithm for global optimization and data clustering applications[J]. Symmetry, 2022, 14(5): 1021. doi: 10.3390/sym14051021
[12]	AGUSHAKA J O, AKINOLA O, EZUGWU A E, et al. Advanced dwarf mongoose optimization for solving CEC 2011 and CEC 2017 benchmark problems[J]. PLoS One, 2022, 17(11): e0275346. doi: 10.1371/journal.pone.0275346
[13]	AGUSHAKA J O, EZUGWU A E, OLAIDE O N, et al. Improved dwarf mongoose optimization for constrained engineering design problems[J]. Journal of Bionic Engineering, 2023, 20(3): 1263-1295. doi: 10.1007/s42235-022-00316-8
[14]	AKINOLA O A, EZUGWU A E, OYELADE O N, et al. A hybrid binary dwarf mongoose optimization algorithm with simulated annealing for feature selection on high dimensional multi-class datasets[J]. Scientific Reports, 2022, 12(1): 14945. doi: 10.1038/s41598-022-18993-0
[15]	贾鹤鸣, 陈丽珍, 力尚龙, 等. 透镜成像反向学习的精英池侏儒猫鼬优化算法[J]. 计算机工程与应用, 2023, 59(24): 131-139. JIA H M, CHEN L Z, LI S L, et al. Optimization algorithm of elite pool dwarf mongoose based on lens imaging reverse learning[J]. Computer Engineering and Applications, 2023, 59(24): 131-139(in Chinese).
[16]	赵世杰, 张红易, 马世林. 领导者引导与支配解进化的多目标矮猫鼬算法[J]. 计算机科学与探索, 2024, 18(2): 403-424. ZHAO S J, ZHANG H Y, MA S L. Multi-objective dwarf mongoose optimization algorithm with leader guidance and dominated solution evolution mechanism[J]. Journal of Frontiers of Computer Science and Technology, 2024, 18(2): 403-424(in Chinese).
[17]	AL-SHOURBAJI I, KACHARE P, FADLELSEED S, et al. Artificial ecosystem-based optimization with dwarf mongoose optimization for feature selection and global optimization problems[J]. International Journal of Computational Intelligence Systems, 2023, 16(1): 102. doi: 10.1007/s44196-023-00279-6
[18]	FU S W, HUANG H S, MA C, et al. Improved dwarf mongoose optimization algorithm using novel nonlinear control and exploration strategies[J]. Expert Systems with Applications, 2023, 233: 120904. doi: 10.1016/j.eswa.2023.120904
[19]	RIZK-ALLAH R M, EL-FERGANY A A, GOUDA E A, et al. Characterization of electrical 1-phase transformer parameters with guaranteed hotspot temperature and aging using an improved dwarf mongoose optimizer[J]. Neural Computing and Applications, 2023, 35(19): 13983-13998. doi: 10.1007/s00521-023-08449-5
[20]	罗淑媛, 张家豪, 宋美佳, 等. 改进矮猫鼬优化算法的特征选择[J]. 龙岩学院学报, 2023, 41(2): 40-46. LUO S Y, ZHANG J H, SONG M J, et al. Improved dwarf mongoose optimization algorithm for feature selection[J]. Journal of Longyan University, 2023, 41(2): 40-46(in Chinese).
[21]	何加文, 许贤泽, 高波. 多策略融合改进的飞蛾火焰优化算法[J]. 北京航空航天大学学报, 2024, 50(9): 2862-2871. HE J W, XU X Z, GAO B. Improved moth-flame optimization algorithm with multi-strategy integration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(9): 2862-2871(in Chinese).
[22]	TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Piscataway: IEEE Press, 2005: 695-701.
[23]	LONG W, JIAO J J, LIANG X M, et al. A random opposition-based learning grey wolf optimizer[J]. IEEE Access, 2019, 7: 113810-113825. doi: 10.1109/ACCESS.2019.2934994
[24]	LI S M, CHEN H L, WANG M J, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future Generation Computer Systems, 2020, 111: 300-323. doi: 10.1016/j.future.2020.03.055
[25]	郭雨鑫, 刘升, 张磊, 等. 精英反向与二次插值改进的黏菌算法[J]. 计算机应用研究, 2021, 38(12): 3651-3656. GUO Y X, LIU S, ZHANG L, et al. Elite opposition-based learning quadratic interpolation slime mould algorithm[J]. Application Research of Computers, 2021, 38(12): 3651-3656(in Chinese).
[26]	任丽莉, 王志军, 闫冬梅. 结合黏菌觅食行为的改进多元宇宙算法[J]. 吉林大学学报(工学版), 2021, 51(6): 2190-2197. REN L L, WANG Z J, YAN D M. Improved multi-verse algorithm with combined slime mould foraging behavior[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(6): 2190-2197(in Chinese).
[27]	HANSEN N. The CMA evolution strategy: a tutorial[EB/OL]. (2016-04-04)[2025-08-18]. https://arxiv.org/abs/1604.00772.
[28]	TANABE R, FUKUNAGA A S. Improving the search performance of SHADE using linear population size reduction[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Piscataway: IEEE Press, 2014: 1658-1665.
[29]	AWAD N H, ALI M Z, SUGANTHAN P N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems[C]//Proceedings of the IEEE Congress on Evolutionary Computation (CEC). Piscataway: IEEE Press, 2017: 372-379.
[30]	蔺文轩, 谢文俊, 张鹏, 等. 基于分组优化改进粒子群算法的无人机三维路径规划[J]. 火力与指挥控制, 2023, 48(1): 20-25. LIN W X, XIE W J, ZHANG P, et al. UAV 3D path planning based on grouping optimization improved particle swarm algorithm[J]. Fire Control & Command Control, 2023, 48(1): 20-25(in Chinese).