-
摘要:
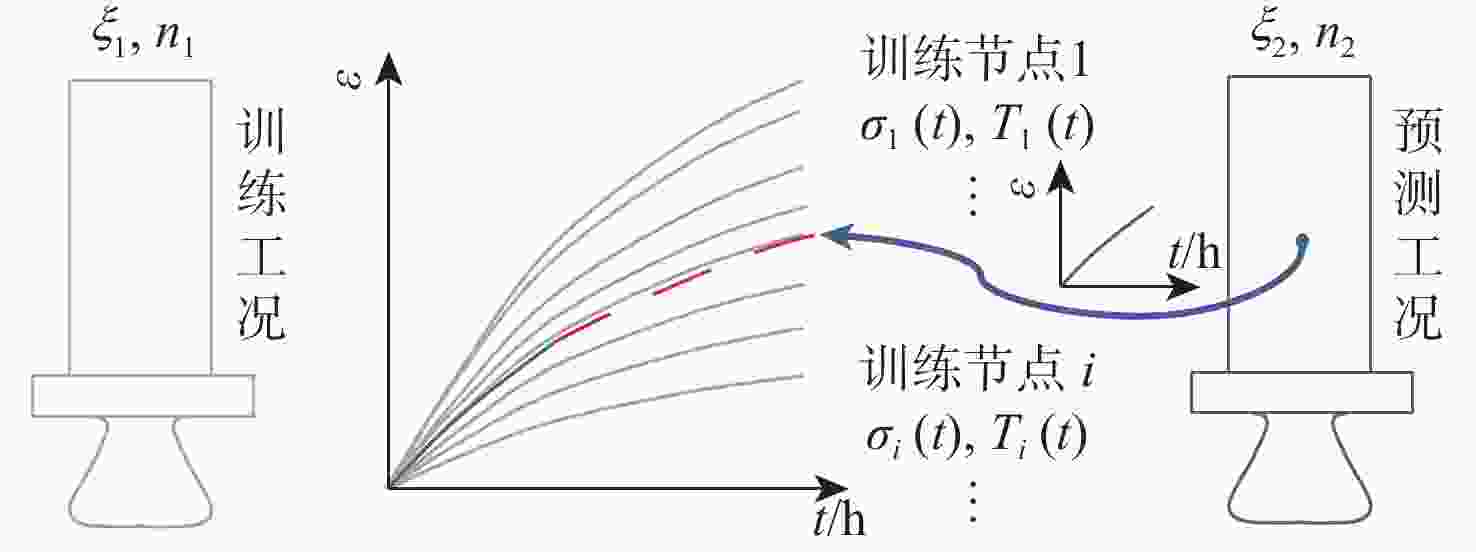
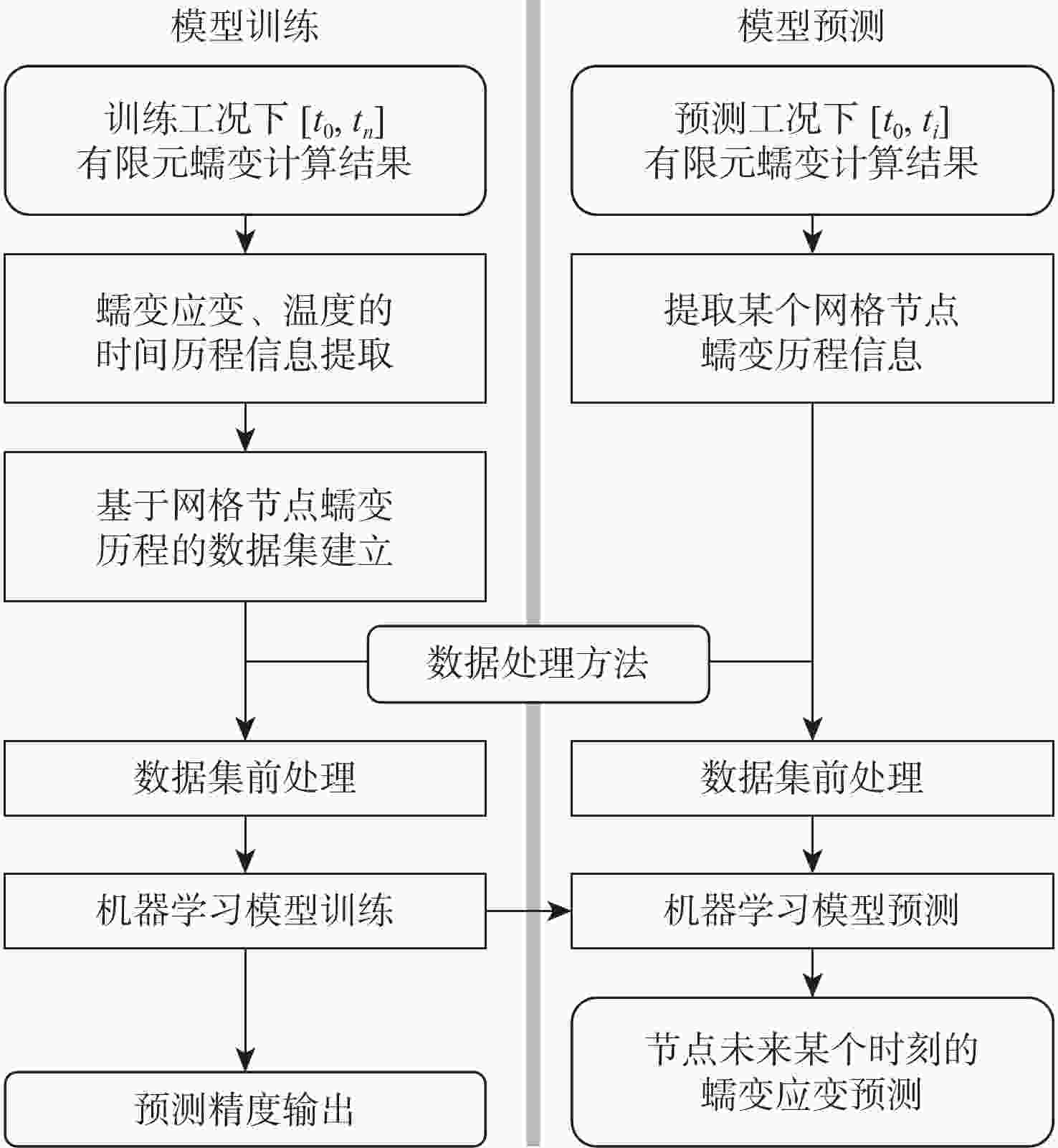
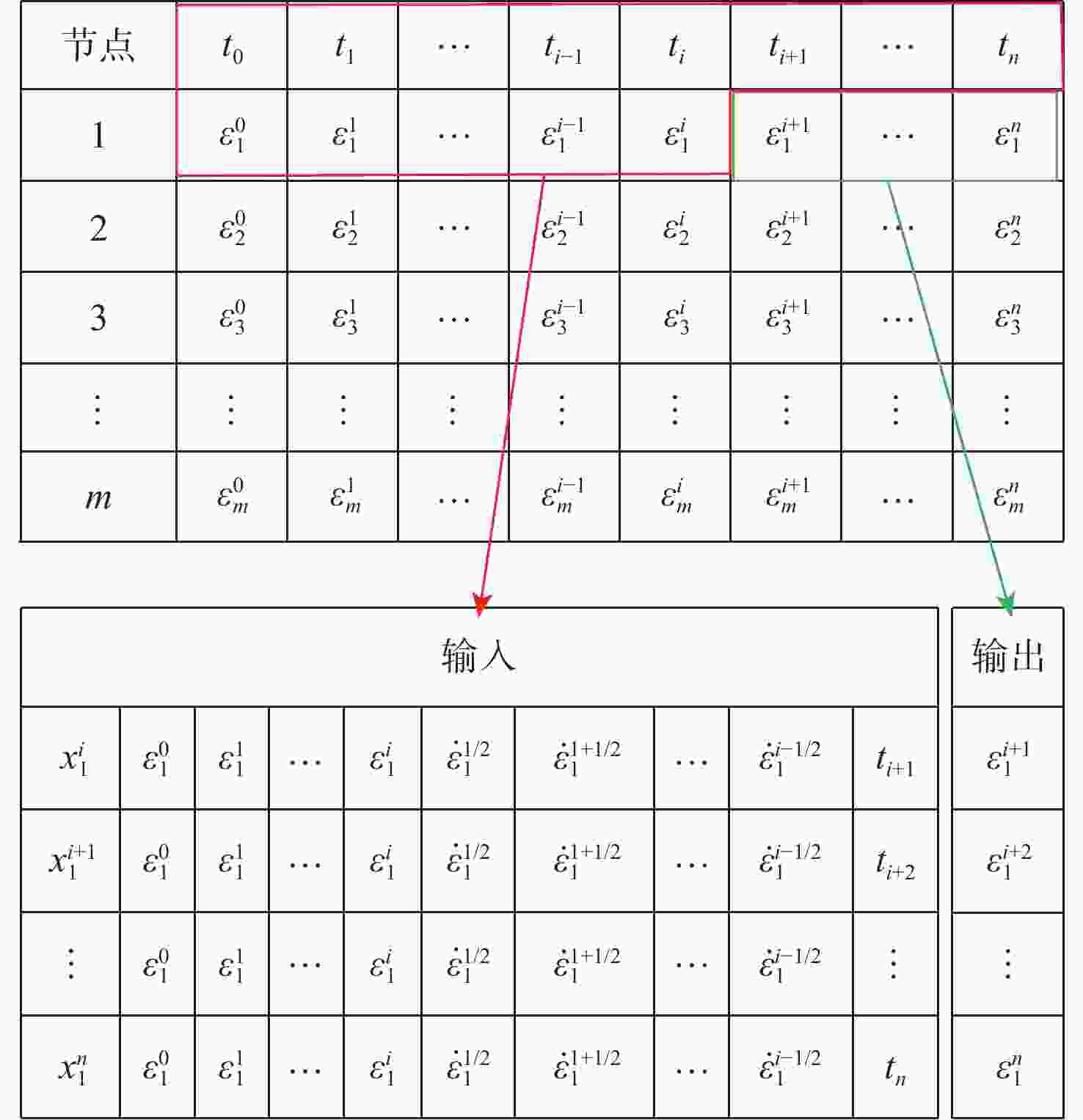
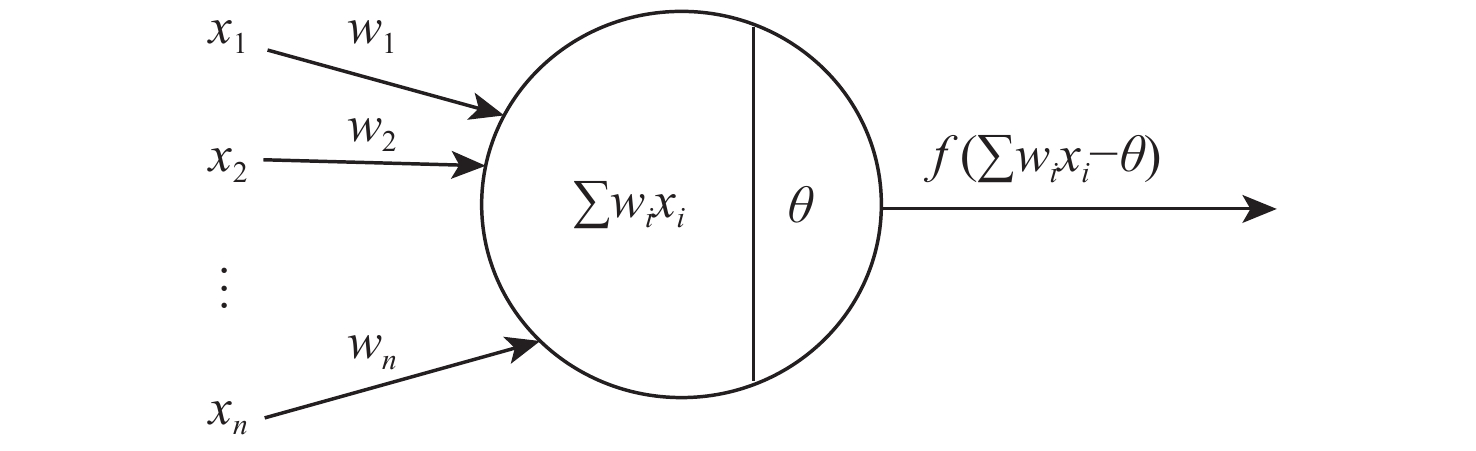
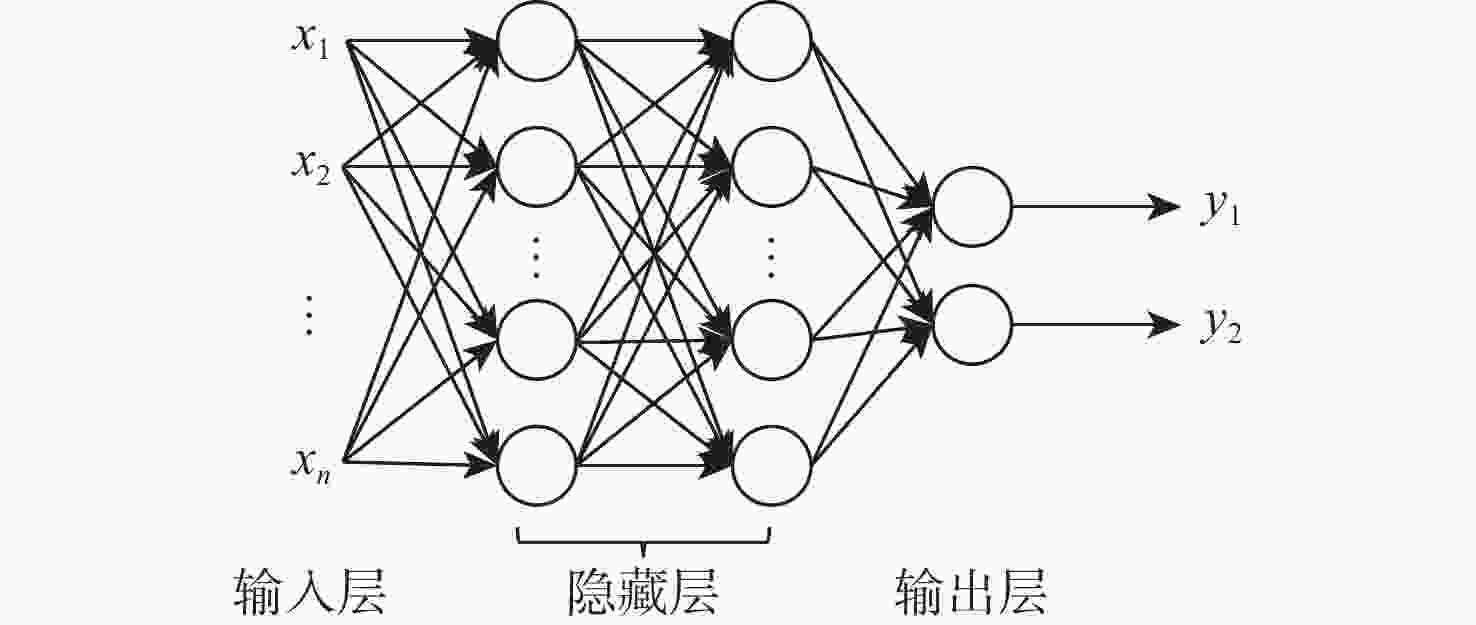
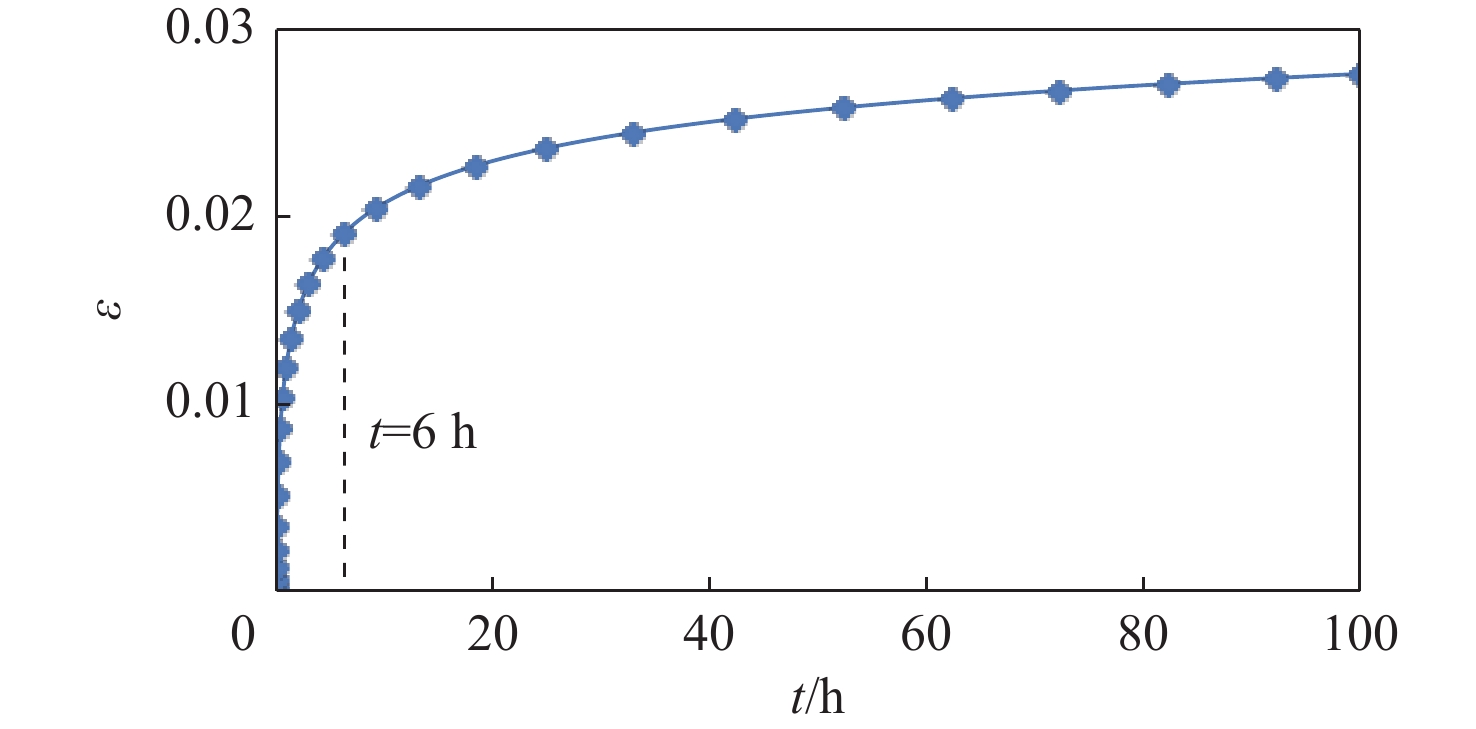
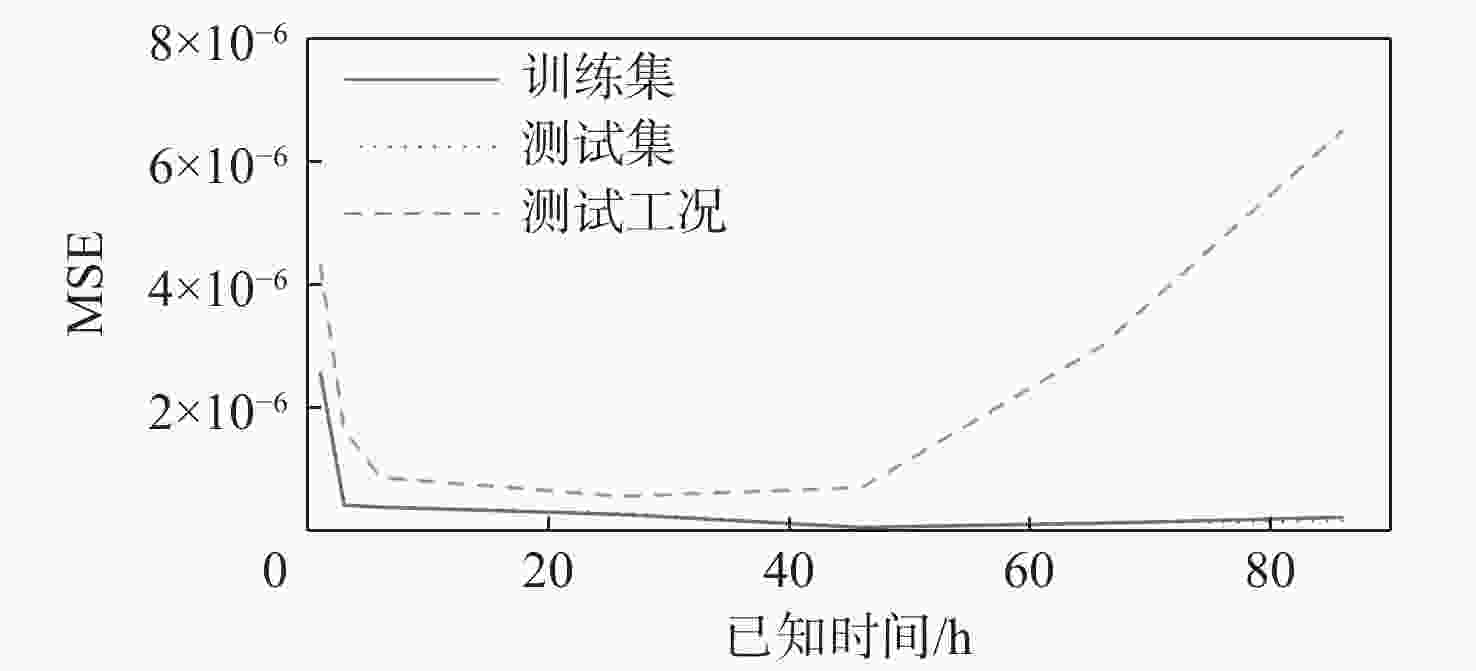
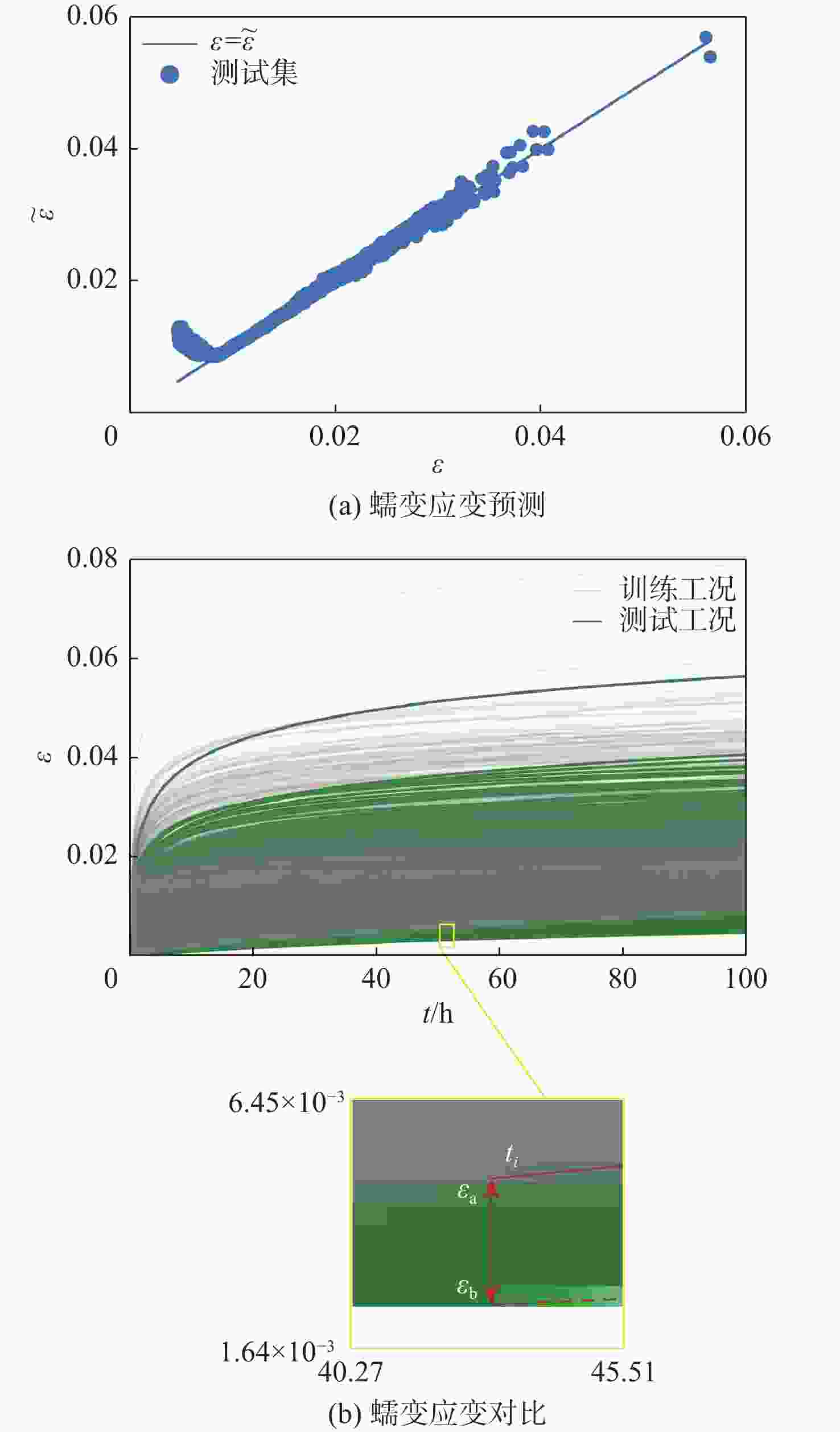
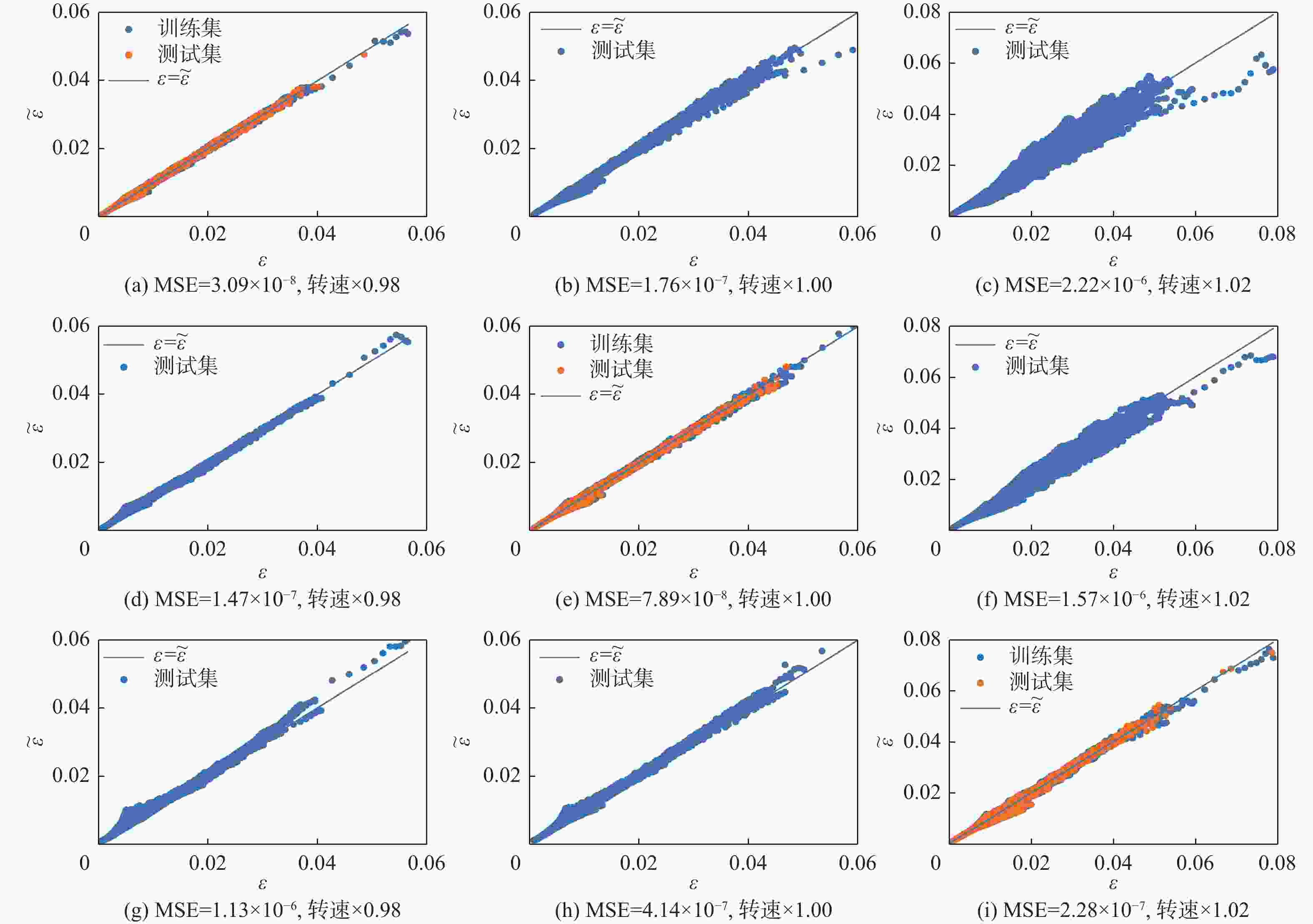
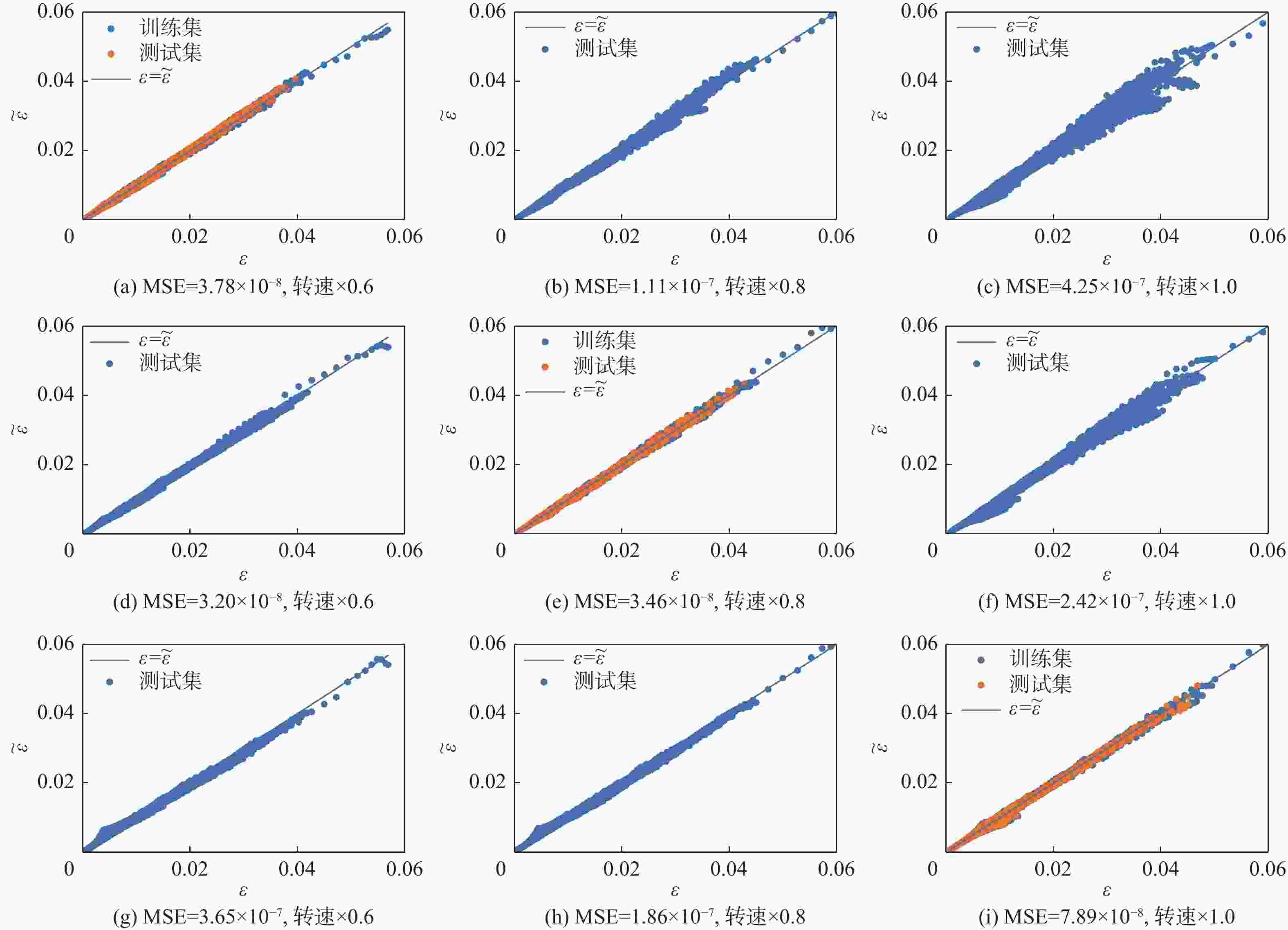
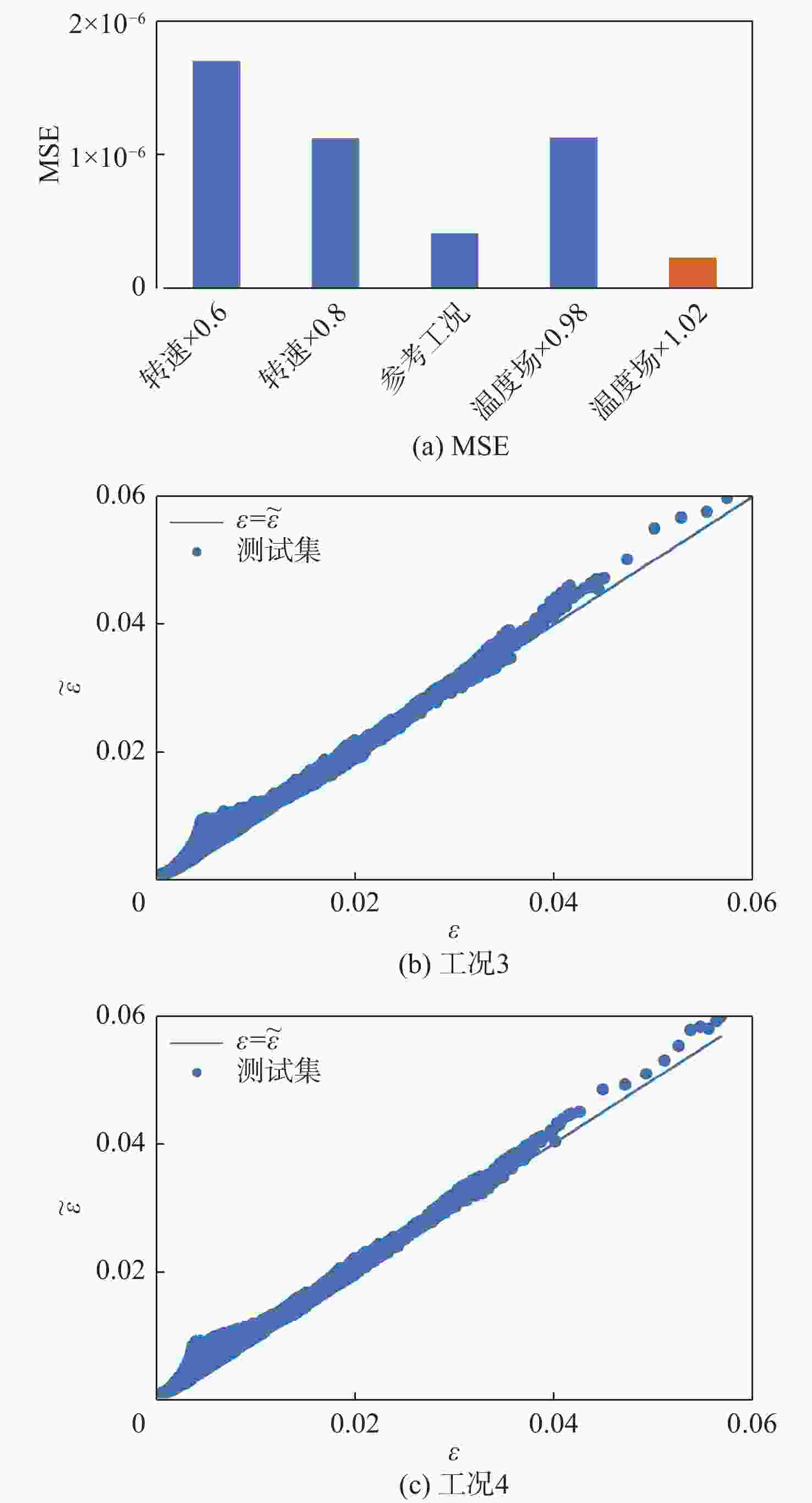
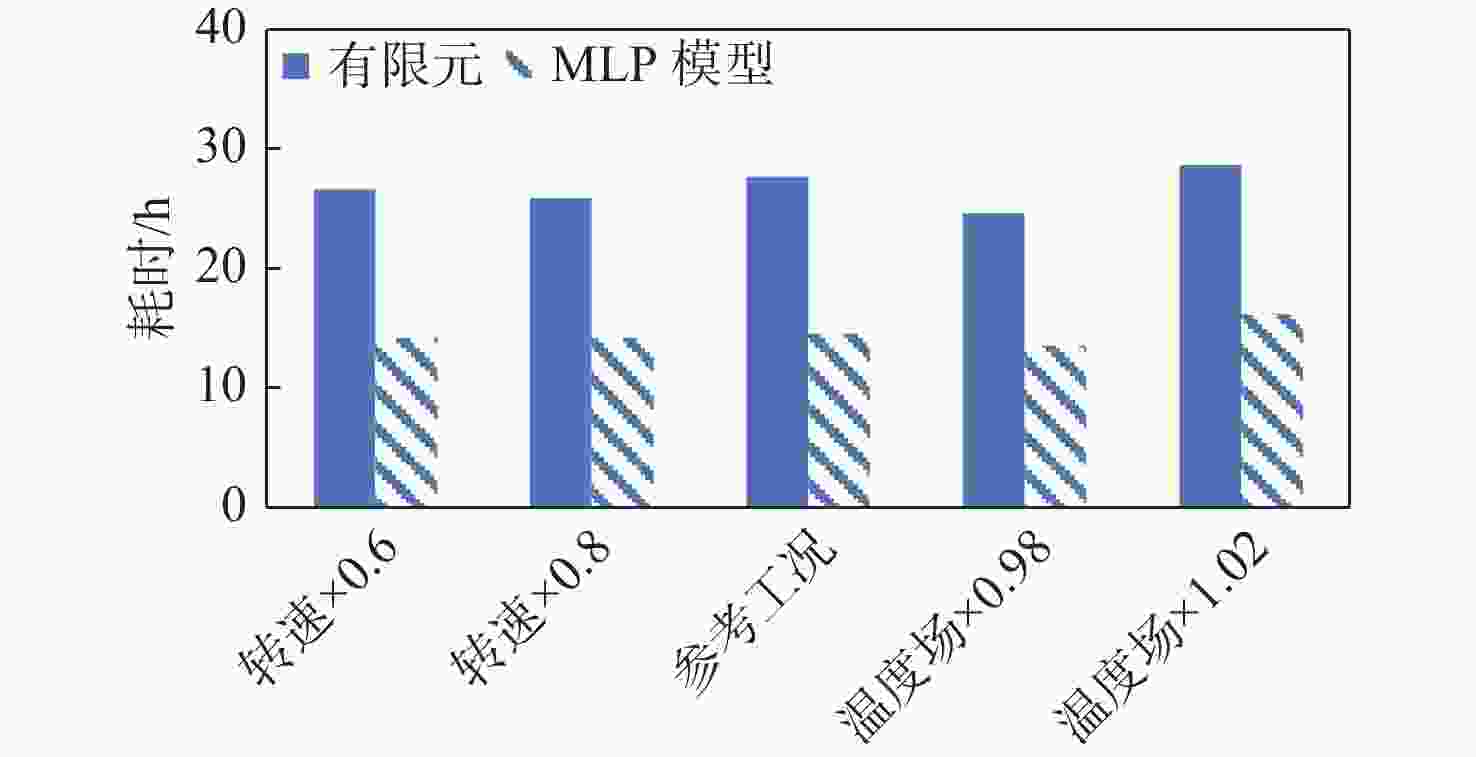
针对涡轮叶片蠕变可靠性分析过程，蠕变有限元计算方法效率不足的问题，提出基于有限元节点的叶片蠕变应变预测原理，并建立了蠕变应变预测多层感知机(MLP)模型，能够根据有限元节点的前期蠕变应变信息预测未来蠕变应变。结果表明：相比于蠕变应变公式拟合方法，所建模型应用机器学习方法，可基于较少时间的蠕变信息预测出较好的结果。通过提高训练工况的温度场和转速水平，可以改善蠕变应变预测模型在预测其他工况时的精度。以最高温度场和转速水平为训练工况，该模型根据前6 h的蠕变信息，预测6～100 h的蠕变应变时，有限元节点蠕变应变较大点的误差约为10%，减少了43%～48%的蠕变应变计算耗时，提高了涡轮叶片蠕变可靠性分析效率。
Abstract:Considering the insufficient efficiency of creep calculation with the finite element methods in the reliability analysis process of turbine blades, a principle for predicting blade creep strain based on the creep information of finite element nodes was proposed. And then a model for creep strain prediction was built based on multilayer perceptron (MLP) learning network. Such model can predict the later creep strain of the finite element nodes according to their earlier creep strain. Compare to the formula fitting method, machine learning method is utilized in the proposed model. Results suggest that the proposed model performed better in the creep prediction with less creep history information. Since more creep history information can be learned in the more sever working condition, it is helpful to improve the performance of machine learning model by enhance the level of temperature field and rotation speed. Finally, the working condition with the highest level of temperature field and rotation speed was regarded as the training condition. The MLP model predicted the creep strain at 6～100 h with the input of creep history information before 6 h, whose error for the finite element nodes with large creep strain was about 10%. And 43%～48% computation time of the finite element computation were economized with the proposed model, which enhance the reliability analysis efficiency of the creep strain of the turbine blade.
-
Key words:
- creep strain /
- finite element nodes /
- machine learning /
- turbine blades /
- efficiency
-
图 10 超温工况下某个网格节点蠕变历程
Figure 10. Creep history of one grid node under overtemperature condition
图 15 温度场对MLP模型预测性能的影响
Figure 15. Effects of temperature field on performance of MLP model
图 16 转速对MLP模型预测性能的影响
Figure 16. Effects of temperature field on performance of MLP model
蠕变模型种类 蠕变本构方程 适用阶段 应变强化模型 $ \dot \varepsilon = {C_1}{\sigma ^{{C_2}}}{\varepsilon ^{{C_3}}}{{\mathrm{e}}^{ - {C_4}/T}} $ 第1阶段 时间强化模型 $ \dot \varepsilon = {C_1}{\sigma ^{{C_2}}}{t^{{C_3}}}{{\mathrm{e}}^{ - {C_4}/T}} $ 第1阶段 修正的应变
强化模型$ \dot \varepsilon = {\left\{ {{C_1}{\sigma ^{{C_2}}}{{\left[ {\left( {{C_3} + 1} \right)\varepsilon } \right]}^{{C_3}}}} \right\}^{1/\left( {{C_3} + 1} \right)}} $ 第1阶段 修正的时间
强化模型$ \dot \varepsilon = {C_1}{\sigma ^{{C_2}}}{t^{{C_3} + 1}}{{\mathrm{e}}^{ - {C_4}/T}}/\left( {{C_3} + 1} \right) $ 第1阶段、第2阶段 Norton模型 $ \dot \varepsilon = {C_1}{\sigma ^{{C_2}}}{{\mathrm{e}}^{ - {C_3}/T}} $ 第2阶段 
下载: 导出CSV
表 2 工况参数
Table 2. Parameters of working conditions
工况 温度场/℃ 转速/(r·min−1) 工况0 1×1.00 1×1.00 工况1 1×0.98 1×1.00 工况2 1×1.02 1×1.00 工况3 1×1.00 1×0.60 工况4 1×1.00 1×0.80
下载: 导出CSV
表 3 不同工况涡轮叶片网格节点蠕变应变范围
Table 3. Range of creep strain of turbine blade element nodes under different working conditions
工况 蠕变应变范围 工况0（温度场×1.00，转速×1.00） 0～ 0.0704 工况1（温度场×0.98） 0～ 0.0564 工况2（温度场×1.02） 0～ 0.0791 工况3（转速×0.6） 0～ 0.0566 工况4（转速×0.8） 0～ 0.0636
下载: 导出CSV
-
[1] 黄聪聪, 徐国强, 闻洁, 等. 基于改进温度评估模型的叶片冷却性能分析[J]. 航空动力学报, 2023, 38(4): 816-829.HUANG C C, XU G Q, WEN J, et al. Analysis of blade cooling performance based on improved temperature assessment model[J]. Journal of Aerospace Power, 2023, 38(4): 816-829(in Chinese). [2] SHENG H L, LIU T, ZHAO Y, et al. New model-based method for aero-engine turbine blade tip clearance measurement[J]. Chinese Journal of Aeronautics, 2023, 36(8): 128-147. doi: 10.1016/j.cja.2022.09.012 [3] ZENG F, ZHANG W H, WANG Y F, et al. Effects of squealer geometry of turbine blade tip on the tip-leakage flow and loss[J]. Journal of Thermal Science, 2021, 30(4): 1376-1387. doi: 10.1007/s11630-021-1488-2 [4] 胡贤明, 嵇大伟, 庄书颖, 等. 本构模型对GH4169缺口件蠕变变形响应计算结果的影响[J]. 航空材料学报, 2021, 41(5): 69-77. doi: 10.11868/j.issn.1005-5053.2021.000086HU X M, JI D W, ZHUANG S Y, et al. Influence of constitutive model on calculation results of creep deformation response of notched specimen of GH4169 alloy[J]. Journal of Aeronautical Materials, 2021, 41(5): 69-77(in Chinese). doi: 10.11868/j.issn.1005-5053.2021.000086 [5] 王雷, 屈平, 黄进浩, 等. 钛合金耐压结构蠕变数值计算方法与试验验证[J]. 船舶力学, 2019, 23(2): 190-199. doi: 10.3969/j.issn.1007-7294.2019.02.008WANG L, QU P, HUANG J H, et al. Creep numerical calculation methods and test verification for pressure structures of titanium alloy[J]. Journal of Ship Mechanics, 2019, 23(2): 190-199(in Chinese). doi: 10.3969/j.issn.1007-7294.2019.02.008 [6] 叶文明. 变载荷历程下蠕变损伤评估方法研究及应用[D]. 南京: 南京航空航天大学, 2020.YE W M. Research and application of creep damage assessment method under variable load history[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020(in Chinese). [7] 李宏新, 王延荣, 程域钊. 基于归一化参数模型的涡轮盘和涡轮叶片蠕变分析[J]. 航空发动机, 2016, 42(5): 48-54.LI H X, WANG Y R, CHENG Y Z. Analysis of creep based on normalized-parameter model for turbine disk and blade[J]. Aeroengine, 2016, 42(5): 48-54(in Chinese). [8] 程域钊, 王延荣, 李宏新, 等. 归一化参数蠕变模型的程序实现与验证[J]. 航空动力学报, 2017, 32(3): 697-703.CHENG Y Z, WANG Y R, LI H X, et al. Implementation and validation of creep model based on normalized parameters[J]. Journal of Aerospace Power, 2017, 32(3): 697-703(in Chinese). [9] WENZLICK M, MAMUN O, DEVANATHAN R, et al. Data science techniques, assumptions, and challenges in alloy clustering and property prediction[J]. Journal of Materials Engineering and Performance, 2021, 30(2): 823-838. doi: 10.1007/s11665-020-05340-5 [10] SANCHEZ S, RENGASAMY D, HYDE C J, et al. Machine learning to determine the main factors affecting creep rates in laser powder bed fusion[J]. Journal of Intelligent Manufacturing, 2021, 32(8): 2353-2373. doi: 10.1007/s10845-021-01785-0 [11] 谢建新, 宿彦京, 薛德祯, 等. 机器学习在材料研发中的应用[J]. 金属学报, 2021, 57(11): 1343-1361.XIE J X, SU Y J, XUE D Z, et al. Machine learning for materials research and development[J]. Acta Metallurgica Sinica, 2021, 57(11): 1343-1361(in Chinese). [12] SHIN D, YAMAMOTO Y, BRADY M P, et al. Modern data analytics approach to predict creep of high-temperature alloys[J]. Acta Materialia, 2019, 168: 321-330. doi: 10.1016/j.actamat.2019.02.017 [13] WANG C H, SUN Z H, ZHAO J Q, et al. Creep deformation constitutive model of bstmuf601 superalloy using BP neural network method[J]. Rare Metal Materials and Engineering, 2020, 49(6): 1885-1893. [14] SUN C, SHI B, WU C, et al. High temperature creep deformation mechanism of bstmuf601 superalloy[J]. Acta Metallurgica Sinica, 2015, 51(3): 349-356. [15] 李福. 航空发动机叶片蠕变寿命可靠性分析及软件系统开发[D]. 沈阳: 东北大学, 2017.LI F. Reliability analysis and software system development of creep life of aero-engine blades[D]. Shenyang: Northeastern University, 2017(in Chinese). [16] 张效成, 宫建国, 轩福贞. 基于机器学习的蠕变断裂寿命预测方法[J]. 压力容器, 2021, 38(7): 48-57. doi: 10.3969/j.issn.1001-4837.2021.07.007ZHANG X C, GONG J G, XUAN F Z. Creep rupture life prediction method based on machine learning[J]. Pressure Vessel Technology, 2021, 38(7): 48-57(in Chinese). doi: 10.3969/j.issn.1001-4837.2021.07.007 [17] HAN H Y, LI W D, ANTONOV S, et al. Mapping the creep life of nickel-based SX superalloys in a large compositional space by a two-model linkage machine learning method[J]. Computational Materials Science, 2022, 205: 111229. doi: 10.1016/j.commatsci.2022.111229 [18] LIU Y, WU J M, WANG Z C, et al. Predicting creep rupture life of Ni-based single crystal superalloys using divide-and-conquer approach based machine learning[J]. Acta Materialia, 2020, 195: 454-467. doi: 10.1016/j.actamat.2020.05.001 [19] ZHU Y L, DUAN F M, YONG W, et al. Creep rupture life prediction of nickel-based superalloys based on data fusion[J]. Computational Materials Science, 2022, 211: 111560. doi: 10.1016/j.commatsci.2022.111560 [20] 王康康, 王小威, 温建锋, 等. 蠕变断裂: 从物理失效机制到结构寿命预测[J]. 机械工程学报, 2021, 57(16): 132-152. doi: 10.3901/JME.2021.16.132WANG K K, WANG X W, WEN J F, et al. Creep rupture: from physical failure mechanisms to lifetime prediction of structures[J]. Journal of Mechanical Engineering, 2021, 57(16): 132-152(in Chinese). doi: 10.3901/JME.2021.16.132 [21] 湛利华, 王萌, 黄明辉. 基于蠕变公式的时效应力松弛行为预测模型[J]. 机械工程学报, 2013, 49(10): 70-76. doi: 10.3901/JME.2013.10.070ZHAN L H, WANG M, HUANG M H. Prediction model for aging stress-relaxation behavior based on creep equations[J]. Journal of Mechanical Engineering, 2013, 49(10): 70-76(in Chinese). doi: 10.3901/JME.2013.10.070 [22] PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: machine learning in python[J]. Journal of Machine Learning Research, 2011, 12: 2825-2830. -
下载:
点击查看大图
计量
- 文章访问数: 207
- HTML全文浏览量: 54
- PDF下载量: 6
- 被引次数: 0
