-
摘要:
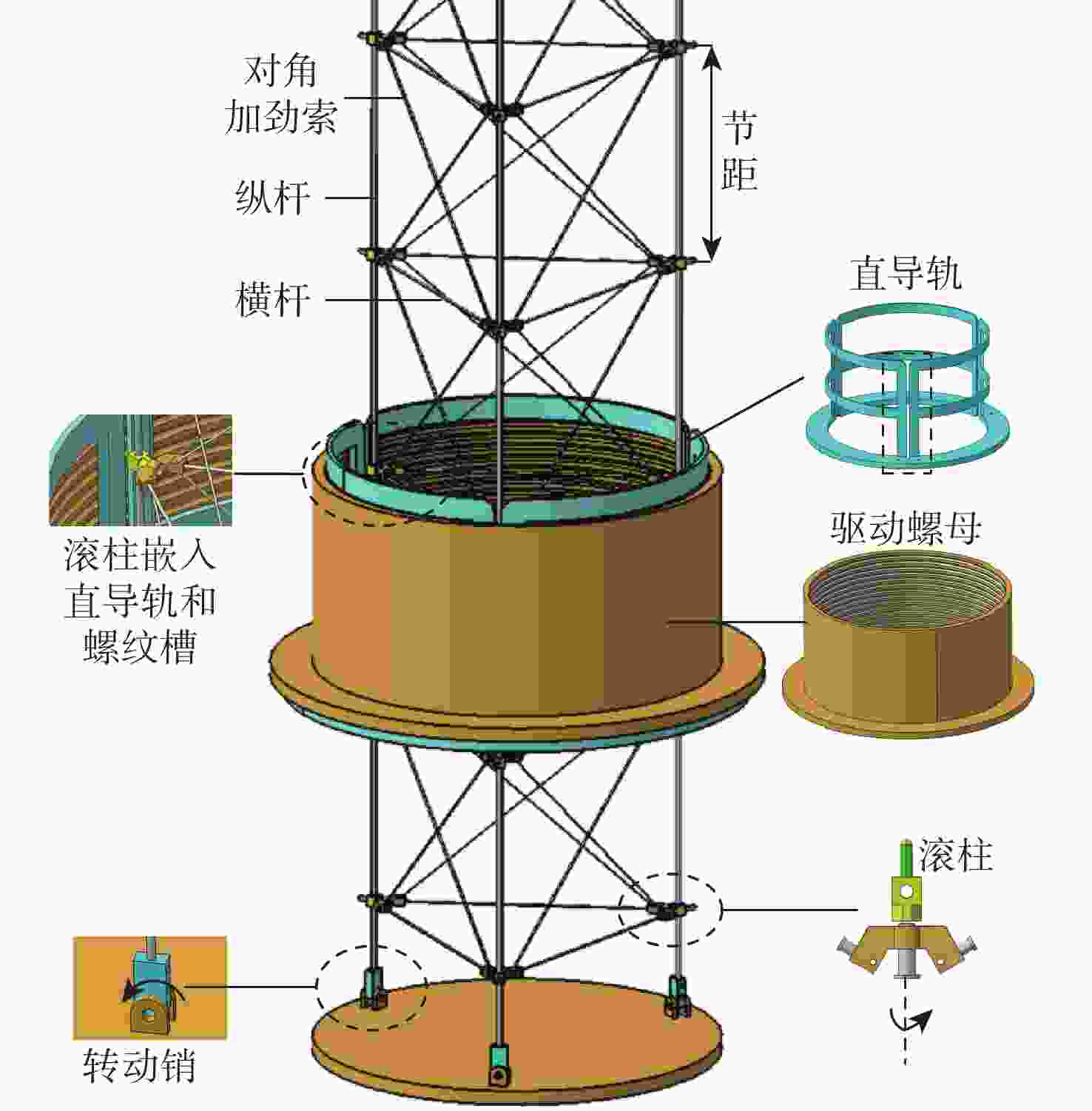
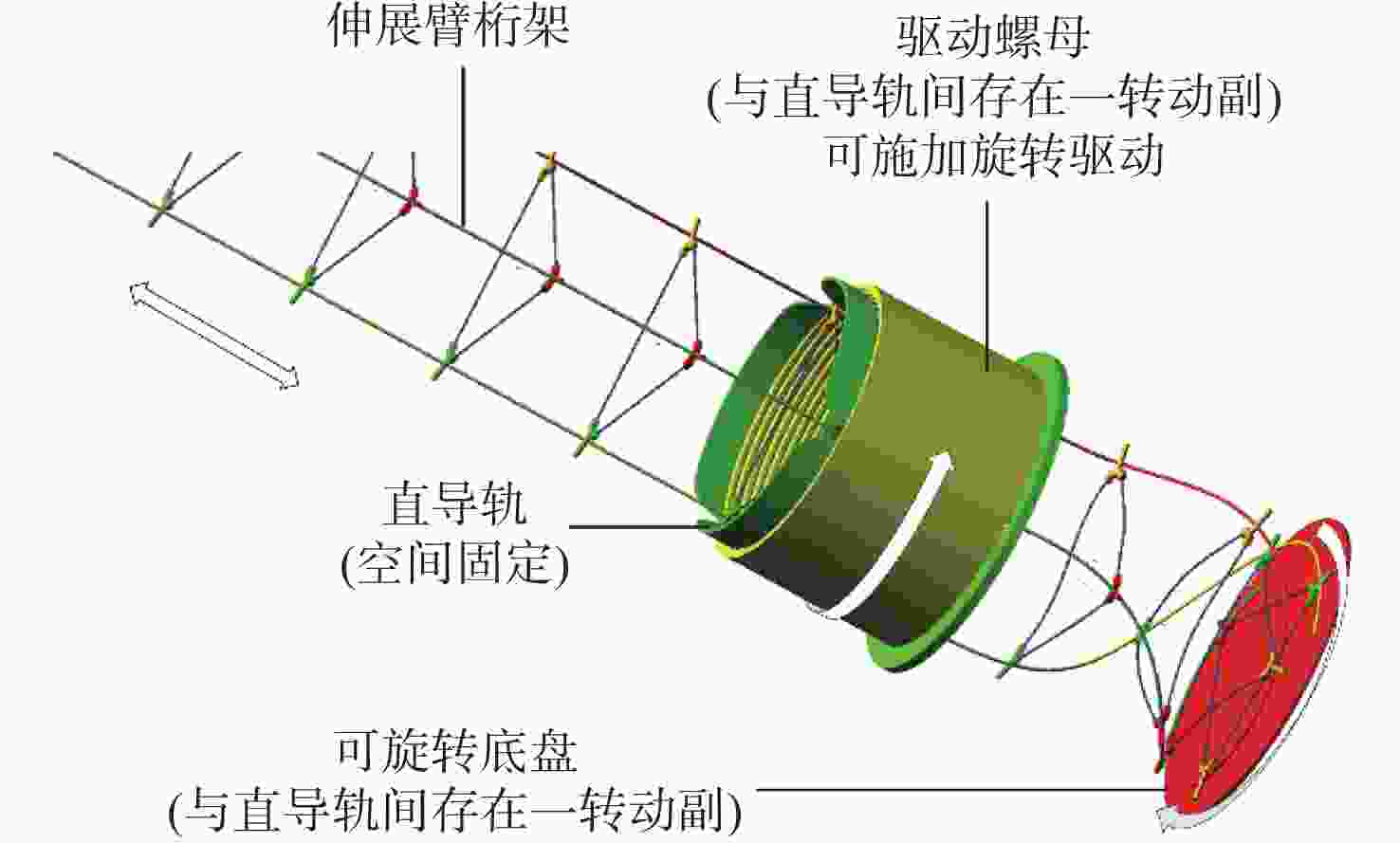
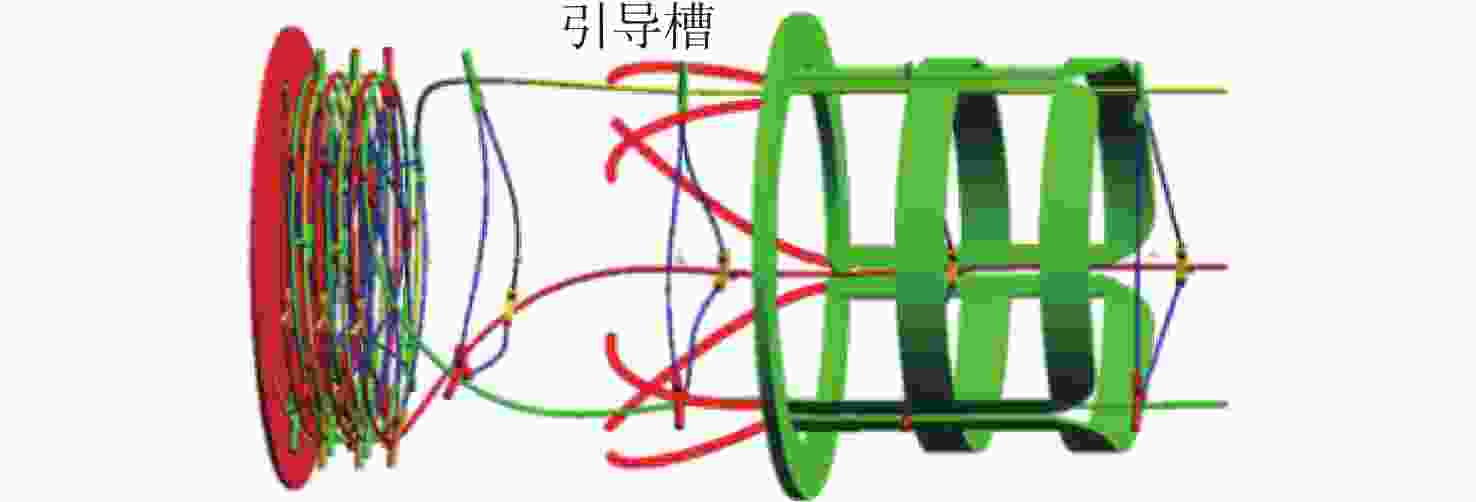
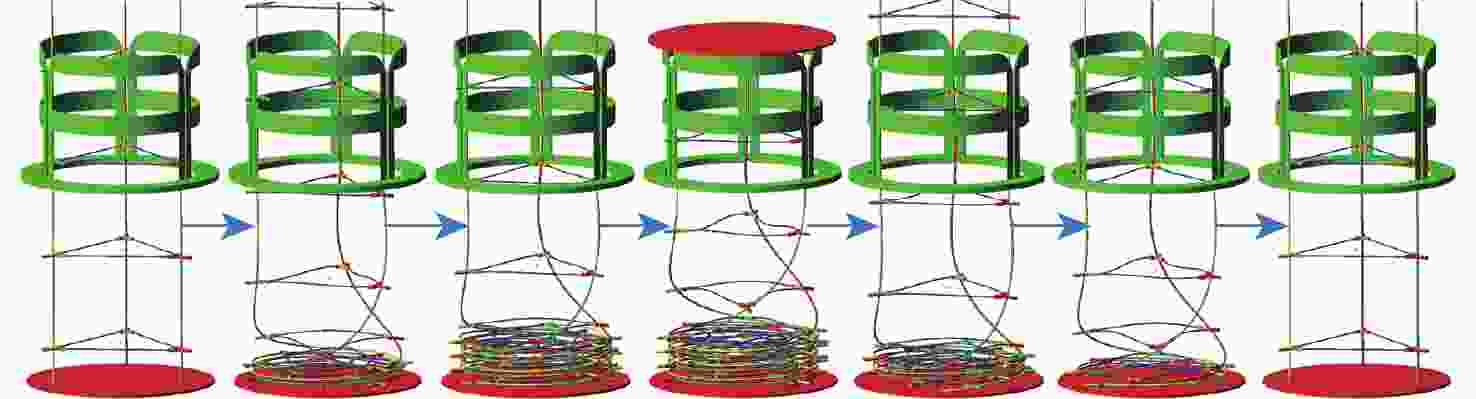
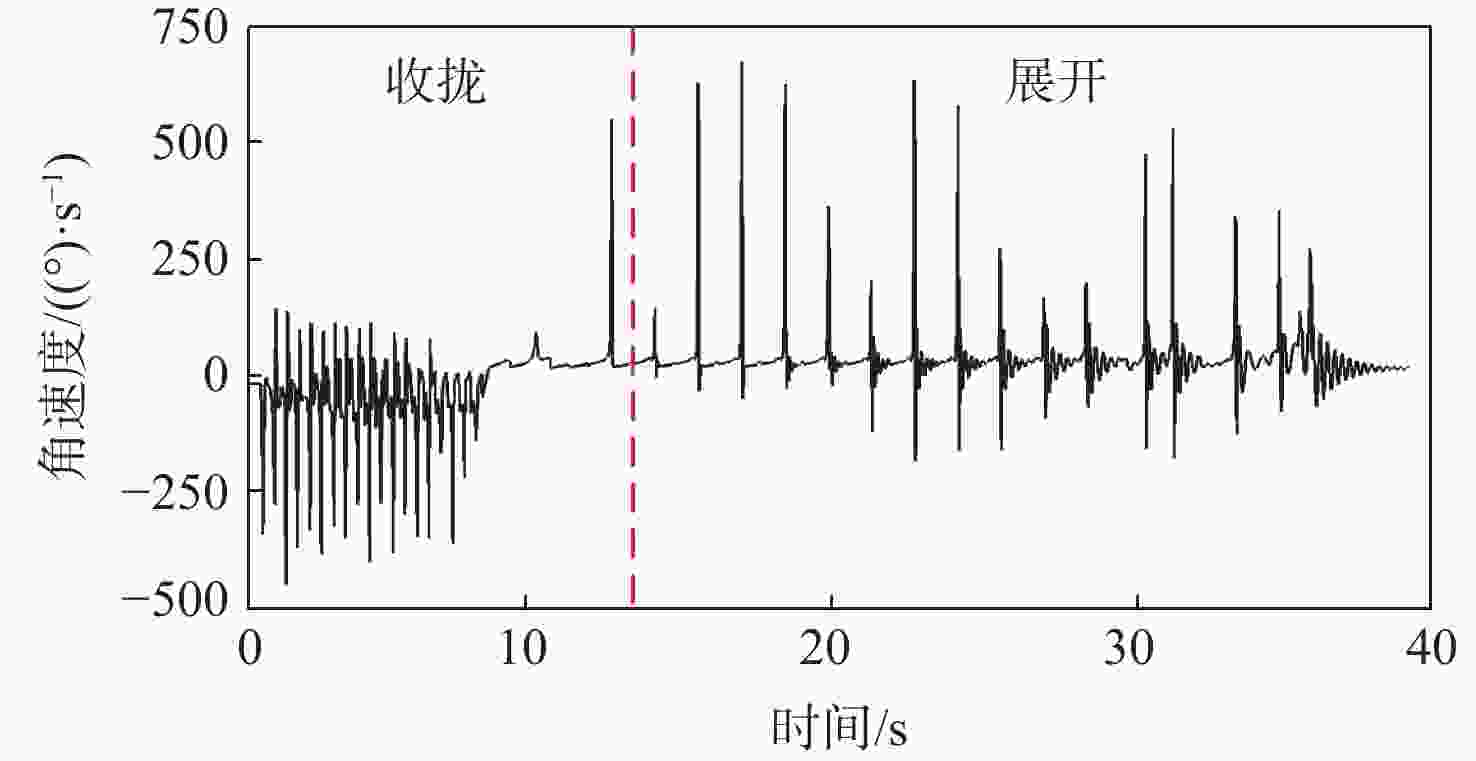
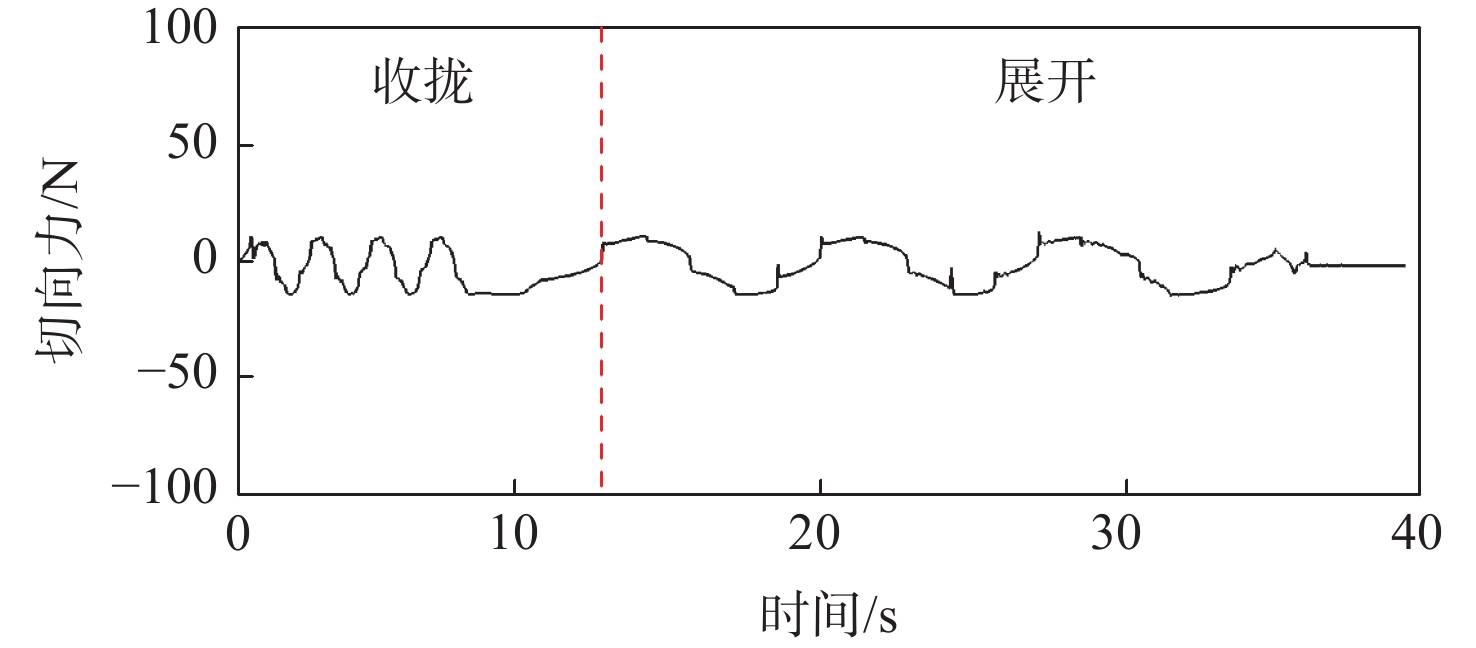
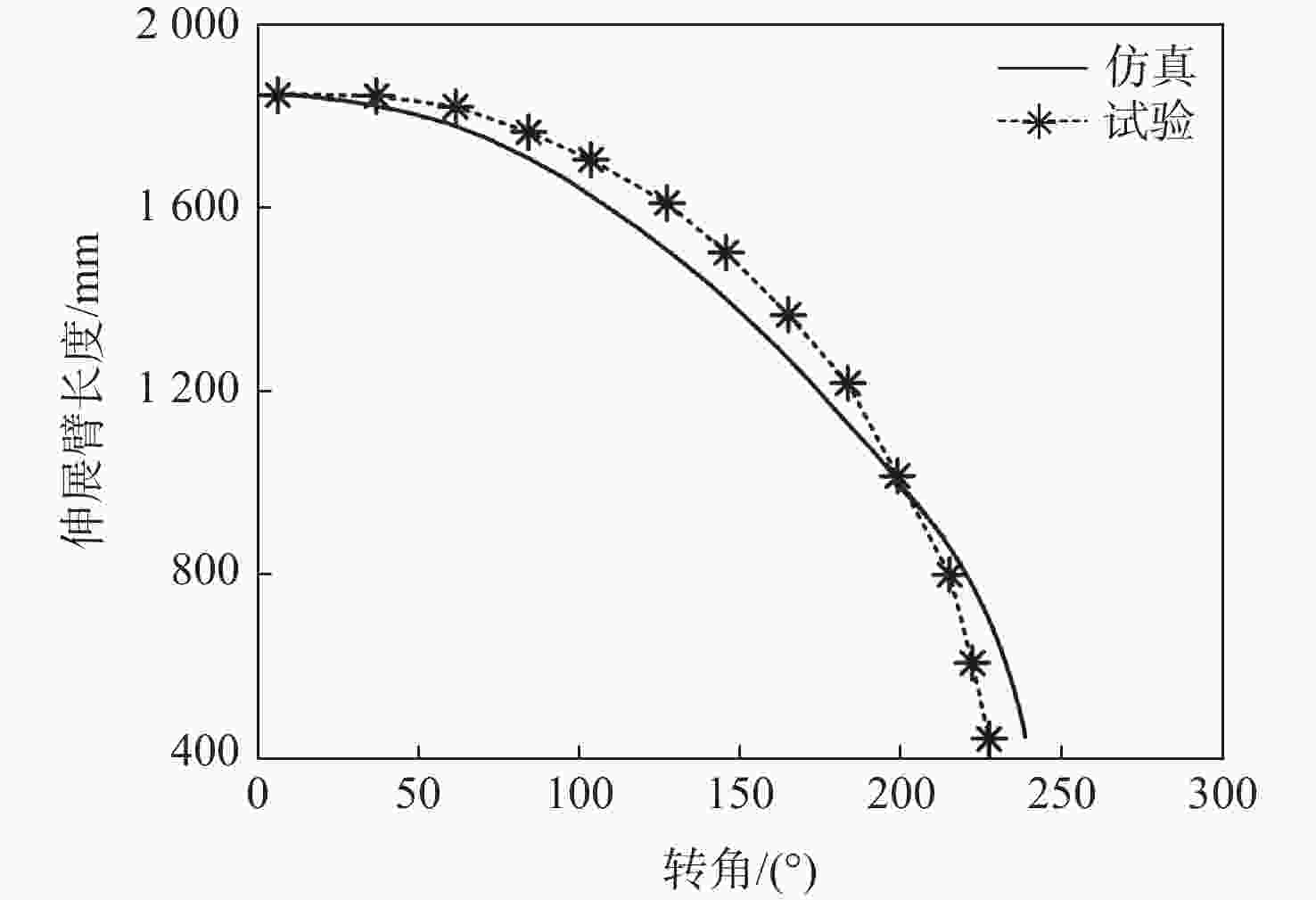
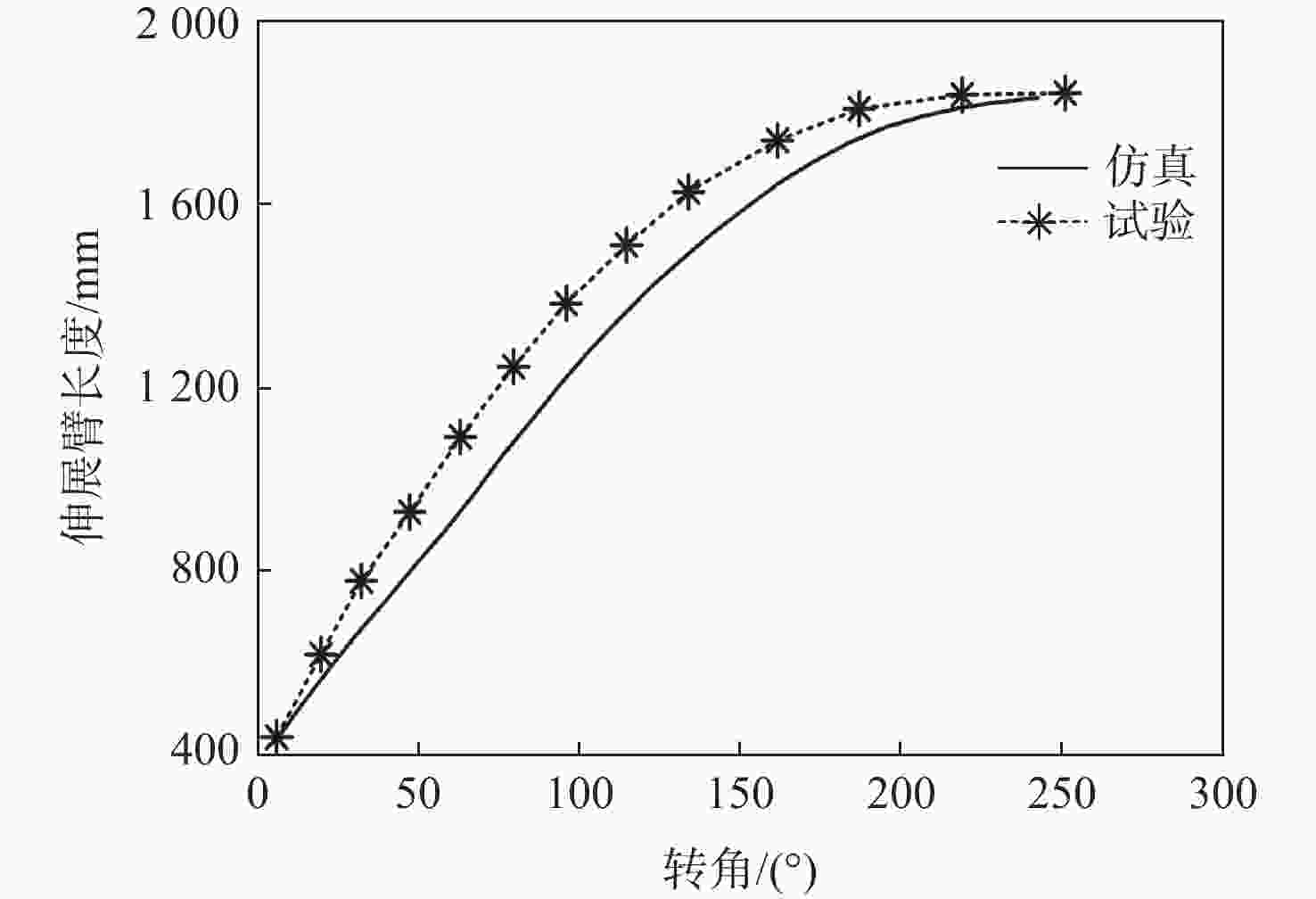
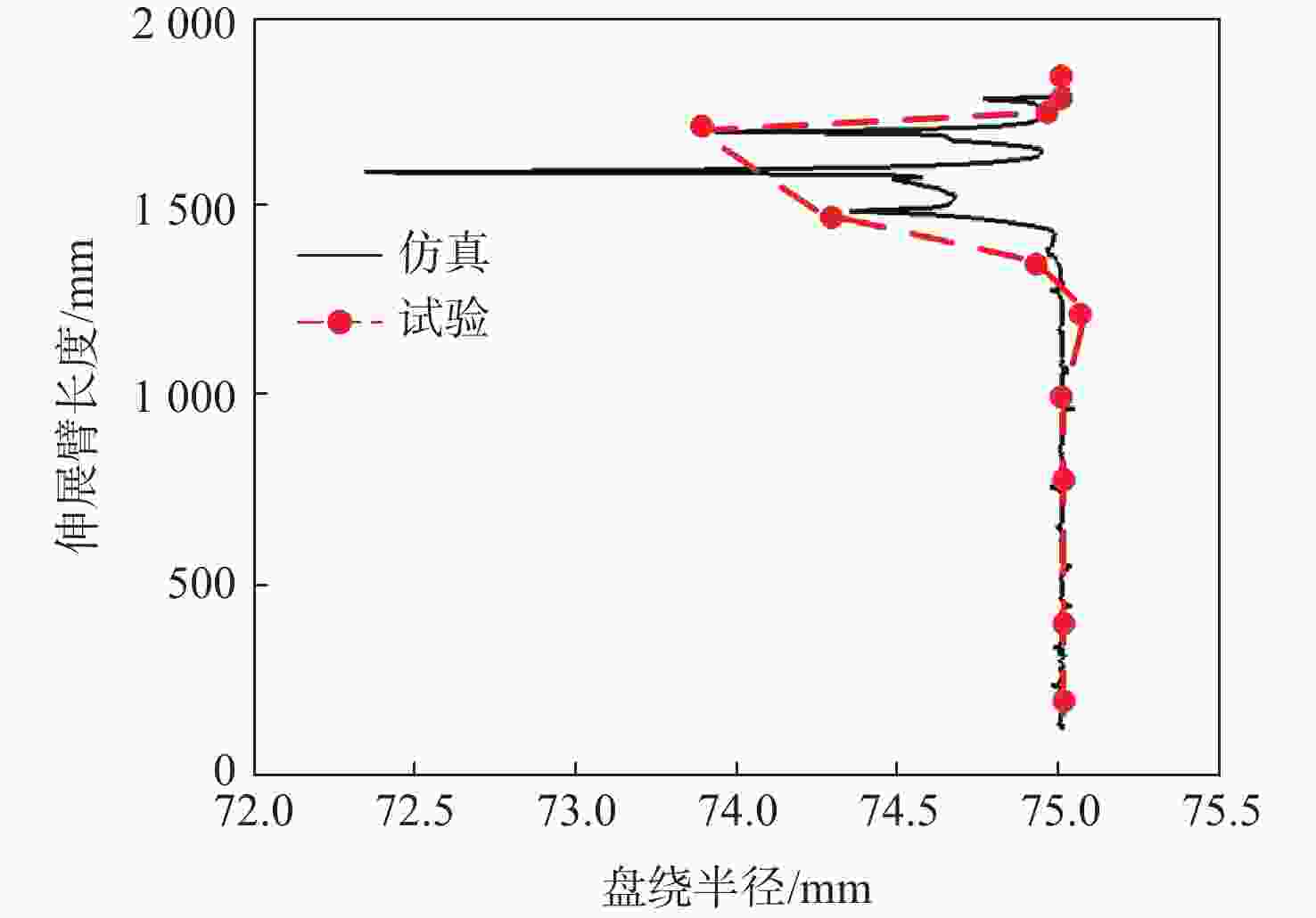
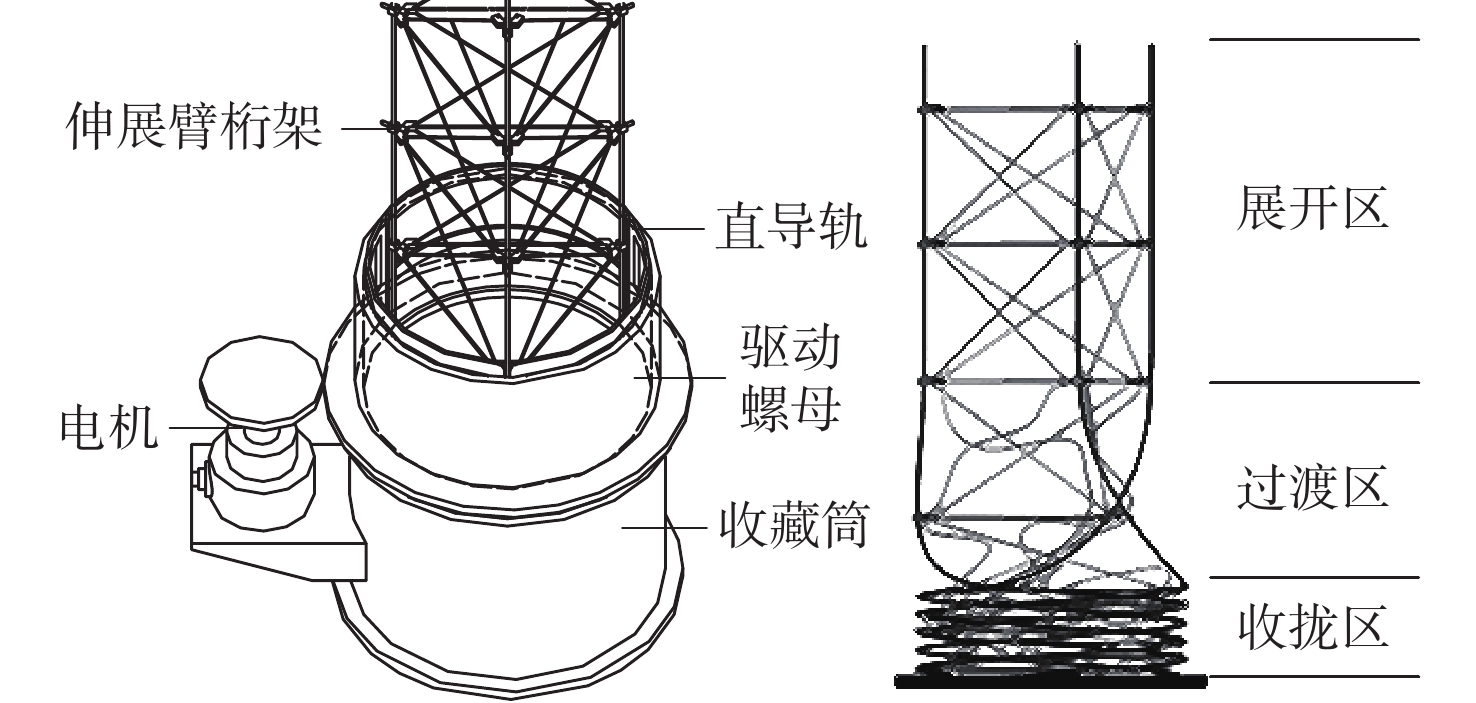
针对螺旋展开盘绕式伸展臂的设计和伸展臂能否顺利收展的关键问题，提出一种螺纹筒和直导轨筒组合作用的套筒型螺旋展开盘绕式伸展臂的研制方案。为预测地面样机的整体性能，采用虚拟样机技术，基于ADAMS软件，建立了套筒型螺旋展开盘绕式伸展臂的动力学仿真模型，对伸展臂的收拢和展开过程进行了仿真分析，并得到了横杆在过渡区处于后屈曲状态的变形特性。通过装配的地面样机进行了伸展臂收拢和展开地面试验，在伸展臂的变形过程中，通过观察三角横框的失稳变形得到了伸展臂利用元件失稳的工作原理，并通过试验方法，将在收展过程中伸展臂长度随底盘转角之间的变化关系曲线，以及伸展臂在过渡区的盘绕半径变化与仿真结果进行了对比，验证了仿真模型的正确性和设计方案的可行性。
-
关键词:
- 螺旋展开盘绕式伸展臂 /
- 收拢展开 /
- 动力学仿真 /
- 过渡区 /
- 地面试验
Abstract:This study suggests the development program of a sleeve type spiral deployment coiled mast using the combination of threaded cylinder and straight guide cylinder, with the goal of designing the sleeve type spiral deployment coiled mast and addressing the crucial issue of whether the mast can be smoothly retracted. In order to predict the overall performance of the ground prototype, this paper adopts the virtual prototype technology, based on ADAMS software, establishes the dynamic simulation model of the sleeve type spiral deployment coiled mast, simulates the retraction and extension process of the mast, and analyzes the deformation characteristics of the crossbar in the transition zone in the post-flexion state. Finally, the ground test of the mast retraction and extension was carried out by the assembled ground prototype. The destabilizing deformation of the triangular cross frame during the mast's deformation process was used to determine the working principle of the mast using elemental instability. The simulation results were compared with the experimentally obtained relationship curves between the change in the mast's length with the chassis angle during the retraction and extension process and the change in the mast's coiled radius in the transition zone, confirming that the simulation model was in the post-flexion state. Comparison is made with the simulation results to verify the correctness of the simulation model and the feasibility of the design scheme.
-
图 1 套筒型螺旋展开盘绕式伸展臂设计
Figure 1. Sleeve type spiral deployment coiled extension arm design
图 31 地面样机收拢展开全过程
Figure 31. The whole process of ground prototype retraction and extension
表 2 不同收藏高度与仿真结果的关系
Table 2. Relationship between different collection height and simulation results
收藏高度/mm 仿真结果 180 收展失败 190 收展失败 195 收展失败 200 收展失败 205 收展失败 210 收展成功 
下载: 导出CSV
表 3 不同横杆半径与仿真结果的关系
Table 3. Relationship between different batten radius and simulation results
横杆半径/mm 仿真结果 0.5 收展失败 0.55 收展失败 0.6 收展失败 0.65 收展成功 0.7 收展成功 0.8 收展成功
下载: 导出CSV
表 4 钛镍合金材料参数
Table 4. Titanium-nickel alloy material parameters
材料性能 参数 密度/(g·cm−3) 6.4～6.5 弹性模量/GPa 28～41 最大回复应力/MPa 600
下载: 导出CSV
-
[1] TIBERT G. Deployable tensegrity structure for space application[D]. Stockholm: KTH Royal institute of technology, 2002. [2] 刘志全, 黎彪, 程刚. 构架式空间可展开支撑臂[J]. 中国空间科学技术, 2011, 31(2): 32-38.LIU Z Q, LI B, CHENG G. Review of deployable-truss masts for space application[J]. China Space Science and Technology, 2011, 31(2): 32-38(in Chinese). [3] 周思达, 周小陈. 空间伸展臂的技术现状与难点[J]. 中国空间科学技术, 2014, 34(6): 38-50. doi: 10.3780/j.issn.1000-758X.2014.06.006ZHOU S D, ZHOU X C. Development and technical difficulties of deployable space masts[J]. Chinese Space Science and Technology, 2014, 34(6): 38-50(in Chinese). doi: 10.3780/j.issn.1000-758X.2014.06.006 [4] WEEKS G E. Dynamic analysis of a deployable space structure[J]. Journal of Spacecraft and Rockets, 1986, 23(1): 102-107. doi: 10.2514/3.25090 [5] BOWDEN M, BENTON M. Design of deployable-truss masts for space station[C]//Proceedings of the Aerospace Design Conference. Reston: AIAA, 1993: 975. [6] EIDEN M, BRUNNER O, STAVRINIDIS C. Deployment analysis of the Olympus astromast and comparison with test measurements[J]. Journal of Spacecraft and Rockets, 1987, 24(1): 63-68. doi: 10.2514/3.25873 [7] 高明星, 刘荣强, 李冰岩, 等. 空间可展开三棱柱伸展臂设计与优化[J]. 机械工程学报, 2020, 56(15): 129-137. doi: 10.3901/JME.2020.15.129GAO M X, LIU R Q, LI B Y, et al. Design and optimization of space deployable tri-prism mast[J]. Journal of Mechanical Engineering, 2020, 56(15): 129-137(in Chinese). doi: 10.3901/JME.2020.15.129 [8] 黄海, 赵旭瑞, 孙亮, 等. 亚太大学生小卫星SSS-1系统设计与在轨试验[J]. 航空学报, 2022, 43(10): 527399. doi: 10.7527/S1000-6893.2022.27399HUANG H, ZHAO X R, SUN L, et al. System design and on-orbit test of Student Small Satellite-1(SSS-1)[J]. Acta Aeronautica et Astro-nautica Sinica, 2022, 43(10): 527399(in Chinese). doi: 10.7527/S1000-6893.2022.27399 [9] MA H B, HUANG H, HAN J B, et al. Study on the criterion to determine the bottom deployment modes of a coilable mast[J]. Acta Astronautica, 2017, 141: 89-97. doi: 10.1016/j.actaastro.2017.09.035 [10] 刘涛, 韩涵, 冀宾, 等. 盘绕式伸展机构非线性屈曲模式的试验研究与数值仿真[J]. 南京航空航天大学学报, 2015, 47(6): 897-903.LIU T, HAN H, JI B, et al. Experimental investigation and numerical simulation on nonlinear buckling mode of coil-able mast[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 897-903(in Chinese). [11] 张金龙, 陈务军, 张大旭, 等. 盘绕式空间伸展臂连续纵杆大转角纯弯曲试验[J]. 哈尔滨工程大学学报, 2015, 36(6): 750-753. doi: 10.3969/j.issn.1006-7043.201310062ZHANG J L, CHEN W J, ZHANG D X, et al. Large rotation pure bending test for the continuous longeron of a coilable space mast[J]. Journal of Harbin Engineering University, 2015, 36(6): 750-753(in Chinese). doi: 10.3969/j.issn.1006-7043.201310062 [12] 韩建斌, 王新升, 马海波. 盘绕式伸展臂展开模式的力学原理[J]. 北京航空航天大学学报, 2013, 39(9): 1168-1173.HAN J B, WANG X S, MA H B. Mechanical principle of the deploying mode for coilable mast[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1168-1173(in Chinese). [13] 李增刚. ADAMS入门详解与实例[M]. 北京: 国防工业出版社, 2009: 125-127.Li Z G. Introduction and examples of ADAMS[M]. Beijing: National Defense Industry Press, 2009: 125-127(in Chinese). [14] 范成建, 熊光明, 周明飞. 虚拟样机软件MSC. ADAMS应用与提高[M]. 北京: 机械工业出版社, 2009: 85-90.FAN C J, XIONG G M, ZHOU M F. Application and improvement of virtual prototyping software MSC. ADAMS[M]. Beijing: China Machine Press, 2009: 85-90(in Chinese). [15] SWOPE R D, AMES W F. Vibrations of a moving threadline[J]. Journal of the Franklin Institute, 1963, 275(1): 36-55. doi: 10.1016/0016-0032(63)90619-7 [16] 刘荣强, 郭宏伟, 邓宗全. 空间索杆铰接式伸展臂设计与试验研究[J]. 宇航学报, 2009, 30(1): 315-320. doi: 10.3873/j.issn.1000-1328.2009.00.057LIU R Q, GUO H W, DENG Z Q. Space cable-strut deployable articutlated mast design and experimental study[J]. Journal of Astronautics, 2009, 30(1): 315-320(in Chinese). doi: 10.3873/j.issn.1000-1328.2009.00.057 [17] 刘延柱, 薛纭. 弹性细杆螺旋线平衡的动态稳定性[J]. 力学季刊, 2005, 26(1): 1-7. doi: 10.3969/j.issn.0254-0053.2005.01.001LIU Y Z, XUE Y. Dynamical stability of helical equilibrium of a thin elastic rod[J]. Chinese Quarterly of Mechanics, 2005, 26(1): 1-7(in Chinese). doi: 10.3969/j.issn.0254-0053.2005.01.001 [18] 苏俊省, 王君杰, 宋彦臣, 等. 钢筋混凝土柱纵筋屈曲长度简化计算模型[J]. 工程力学, 2017, 34(2): 162-170. doi: 10.6052/j.issn.1000-4750.2015.08.0634SU J S, WANG J J, SONG Y C, et al. Simplified calculation model of longitudinal reinforcement buckling length in RC columns[J]. Engineering Mechanics, 2017, 34(2): 162-170(in Chinese). doi: 10.6052/j.issn.1000-4750.2015.08.0634 [19] TIMOSHENKO S P, GERE J M. Theory of elastic stability[M]. New York: Courier Corporation, 2012: 76-81. -
下载:
点击查看大图
计量
- 文章访问数: 247
- HTML全文浏览量: 70
- PDF下载量: 5
- 被引次数: 0
