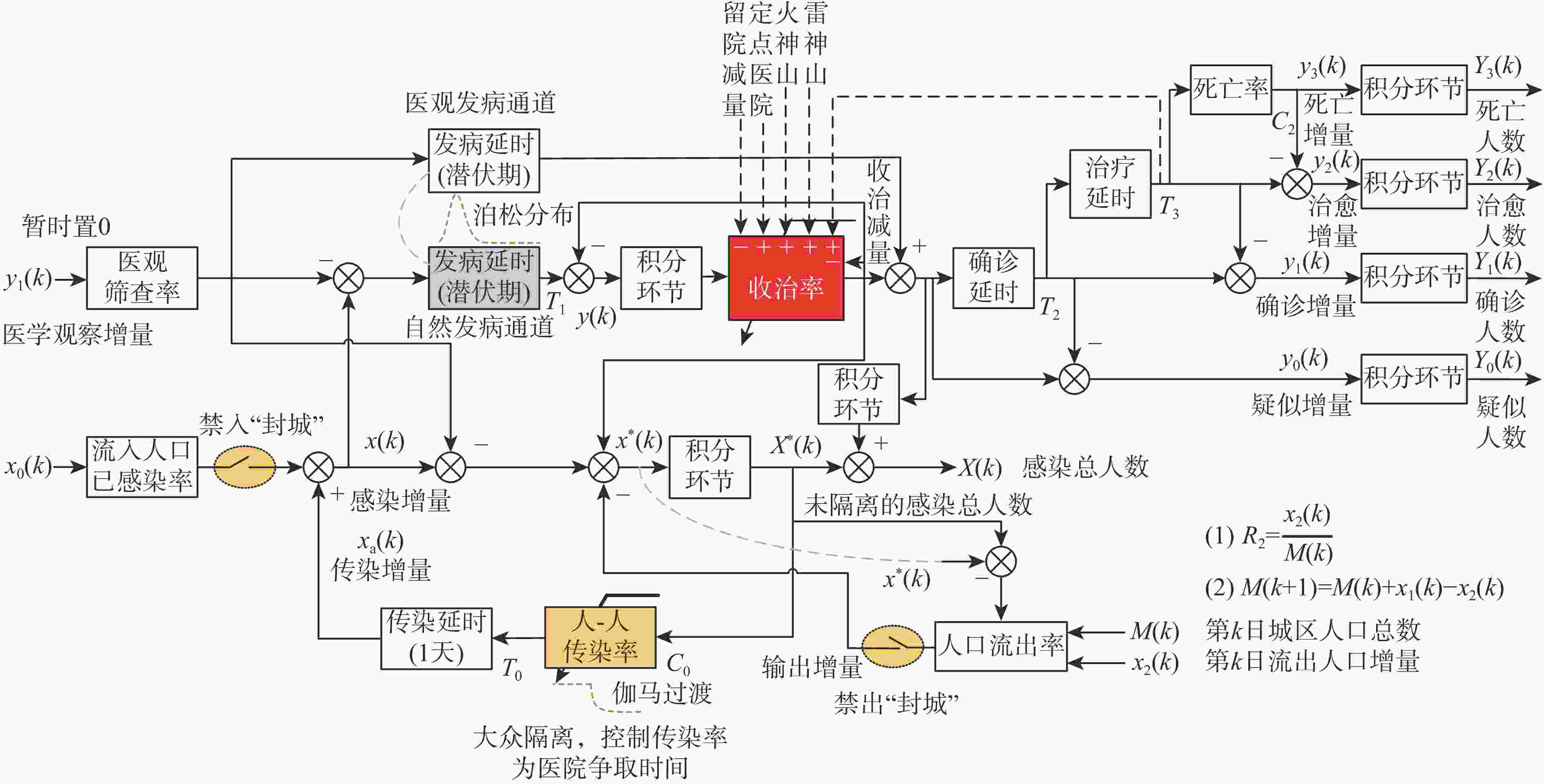
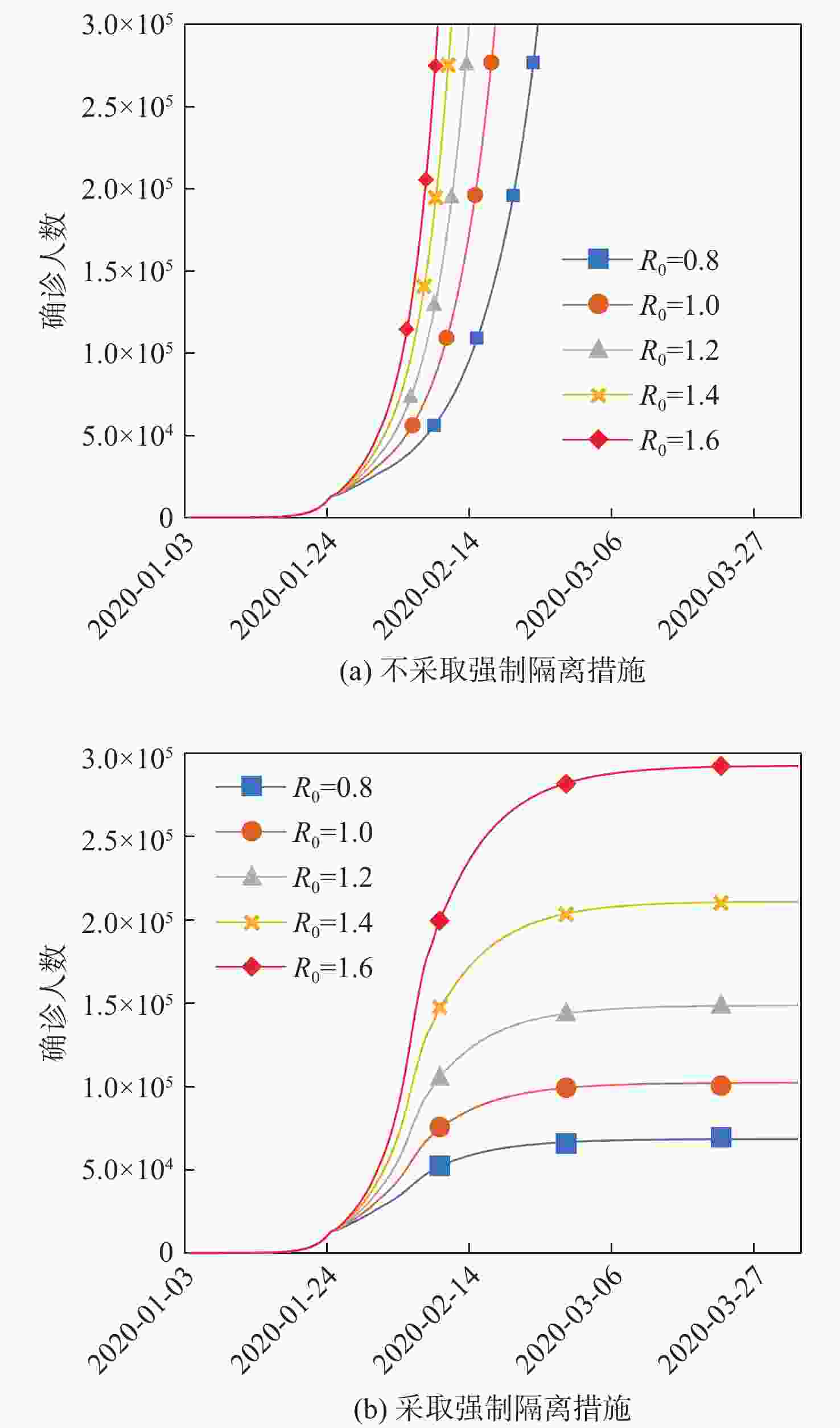
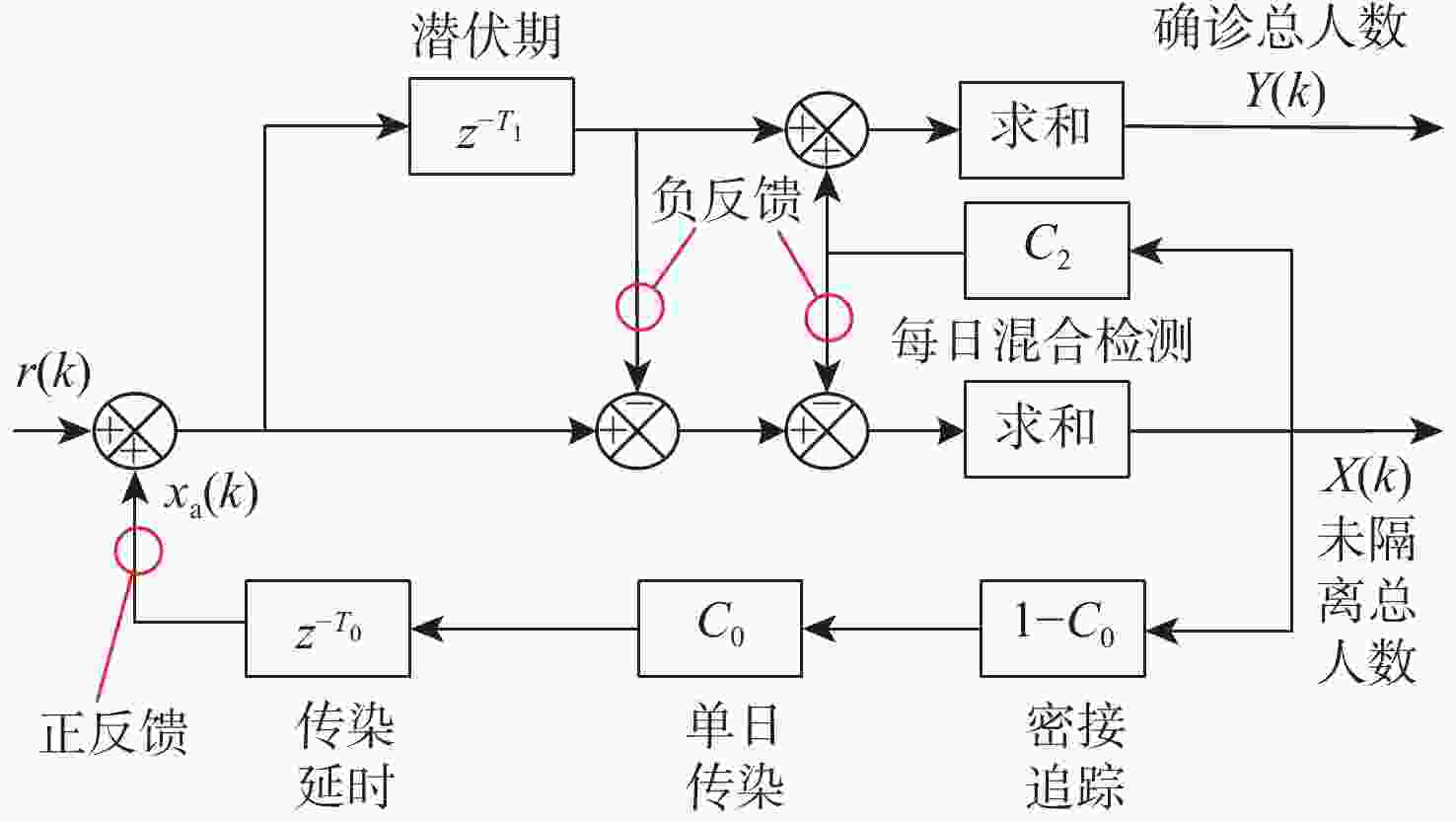
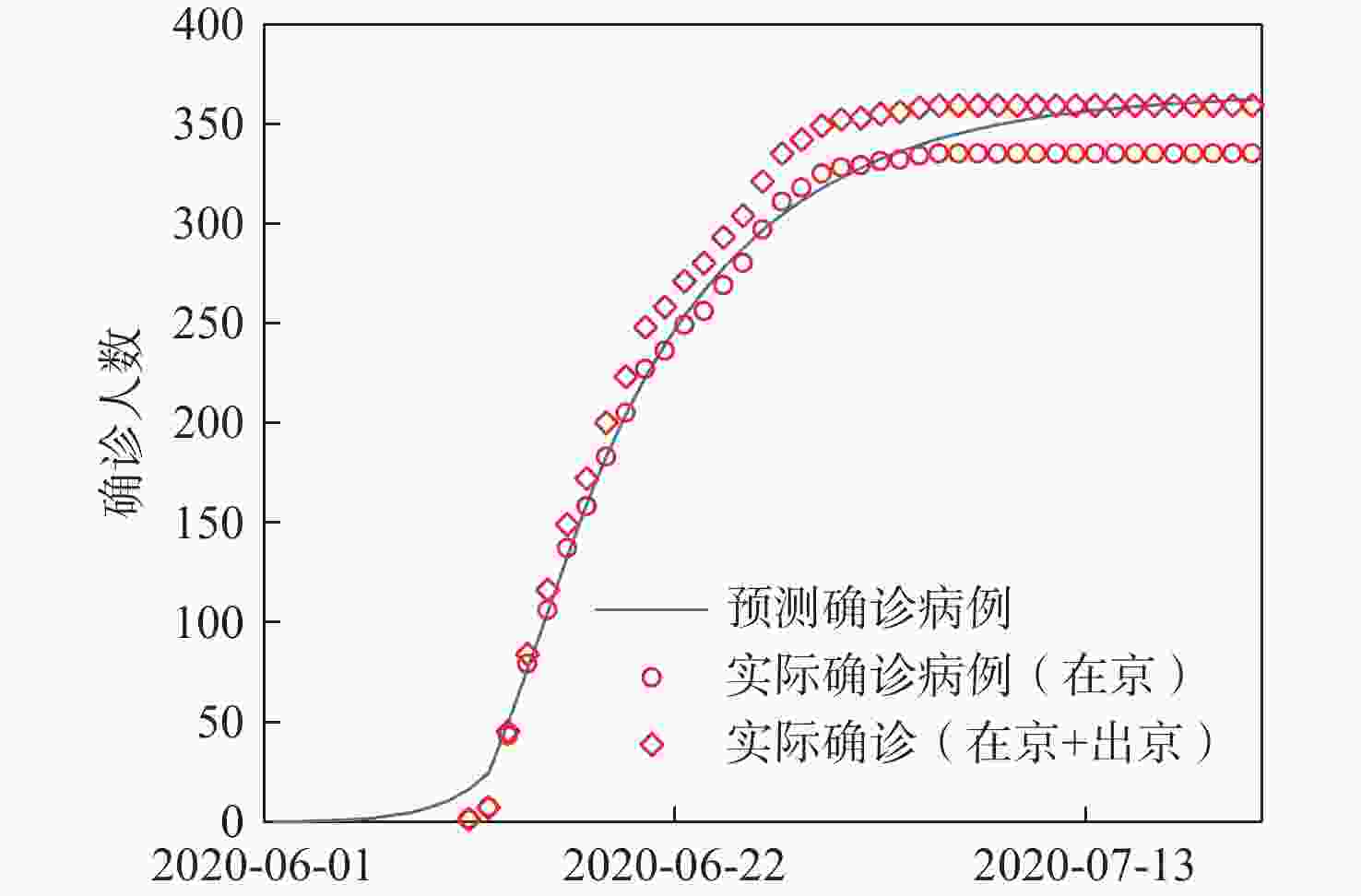
Control system model of COVID-19 and its application in predicting the epidemic outbreak
-
摘要:
自2020年1月以来，全世界经历了超过3年的百年一遇的疫情影响。随着严重急性呼吸综合征冠状病毒2 (SARS-CoV-2)，即俗称新冠病毒的变异，全球的防控策略也随之发生了巨大的变化。回顾整个疫情防控过程，新冠病毒的每次变异，都有可能给下一步的疫情防控政策带来巨大的挑战。因此，如何确定最佳的防疫措施也逐渐成为防疫成败的关键，而如何更早地预测出疫情发展趋势及推论出合理的防疫措施也就具有极大的价值。以经典控制理论为基础，通过构建的严重急性呼吸综合征(SARS)及新冠不同变异毒株的疫情传染模型，旨在揭示疫情传播的内部机理，并解释各类防控措施的干预机制及成效分析。与疫情分析领域常用的易感-感染-康复/易感-潜伏-感染-康复(SIR/SEIR)等模型不同，所建模型的最大作用不在于精确地预测最终的感染人数，而在于其更早的提出风险预警，以及精准的建议防疫控制措施的能力。期望可以利用控制系统模型揭示本轮新冠疫情传播的部分规律，将控制理论引入到未来的疫情防控事业当中去，以达到提前预警、动态防控的目的。
Abstract:Since January 2020, the world has experienced the impact of the once-in-a-century pandemic for over three years. With the variation of the severe acute respiratory syndrome coronavirus 2(SARS-CoV-2), it is commonly known as the variation of COV1D-19, the global prevention and control strategy has also undergone tremendous changes. Reviewing the whole epidemic prevention and control process, every mutation of the COVID-19 probably brings huge challenges to the next epidemic prevention and control policy. Thus, the key to the success or failure of epidemic prevention has gradually changed to identifying the appropriate methods. It is also very valuable to foresee the epidemic's development pattern in advance and to derive plausible measures to avoid epidemics. Based on classical control theory, this paper aims to reveal the internal mechanism of epidemic transmission, and explain the intervention mechanism and effectiveness analysis of various prevention and control measures by constructing the epidemic infection model of severe acute respiratory syndrome (SARS) and the COVID-19 different variants. In contrast to the widely used susceptible-infected-recovered/susceptible-exposed-infected recovered (SIR/SEIR) models in the field of epidemic analysis, the constructed model's strength is in its capacity to effectively prescribe epidemic prevention and control measures and to provide early risk alerts, rather than on its ability to predict the ultimate number of infections. This paper expects that the control system model can be used to reveal some laws of the spread of this round of the COVID-19 epidemic, so that control theory can be introduced into future epidemic prevention and control cases to achieve the purpose of early warning and dynamic prevention and control.
-
Key words:
- COVID-19 /
- control system model /
- epidemic model /
- epidemic prediction /
- Laplace transform
-
图 8 上海模型的拟合与预测曲线（预测时间为2020-01-28）
Figure 8. Fitting and prediction curve of Shanghai model (predicted on 28th January 2020)
图 9 全国（除湖北外）、北京、重庆及温州的疫情发展曲线（预测时间为2020-01-28）
Figure 9. Epidemic curve in China (except Hubei), Beijing, Chongqing and Wenzhou (predicted on 28th January, 2020)
图 12 加入密接追踪与混合检测的新冠疫情模型
Figure 12. COVID-19 epidemic model with contact tracing and nucleic acid testing
图 14 2021年7月利用动态参数辨识的南京与扬州疫情分析
Figure 14. Epidemic analysis of Nanjing and Yangzhou using dynamic parameter identification in July 2021
表 1 上海模型仿真参数设置
Table 1. Shanghai model simulation parameters
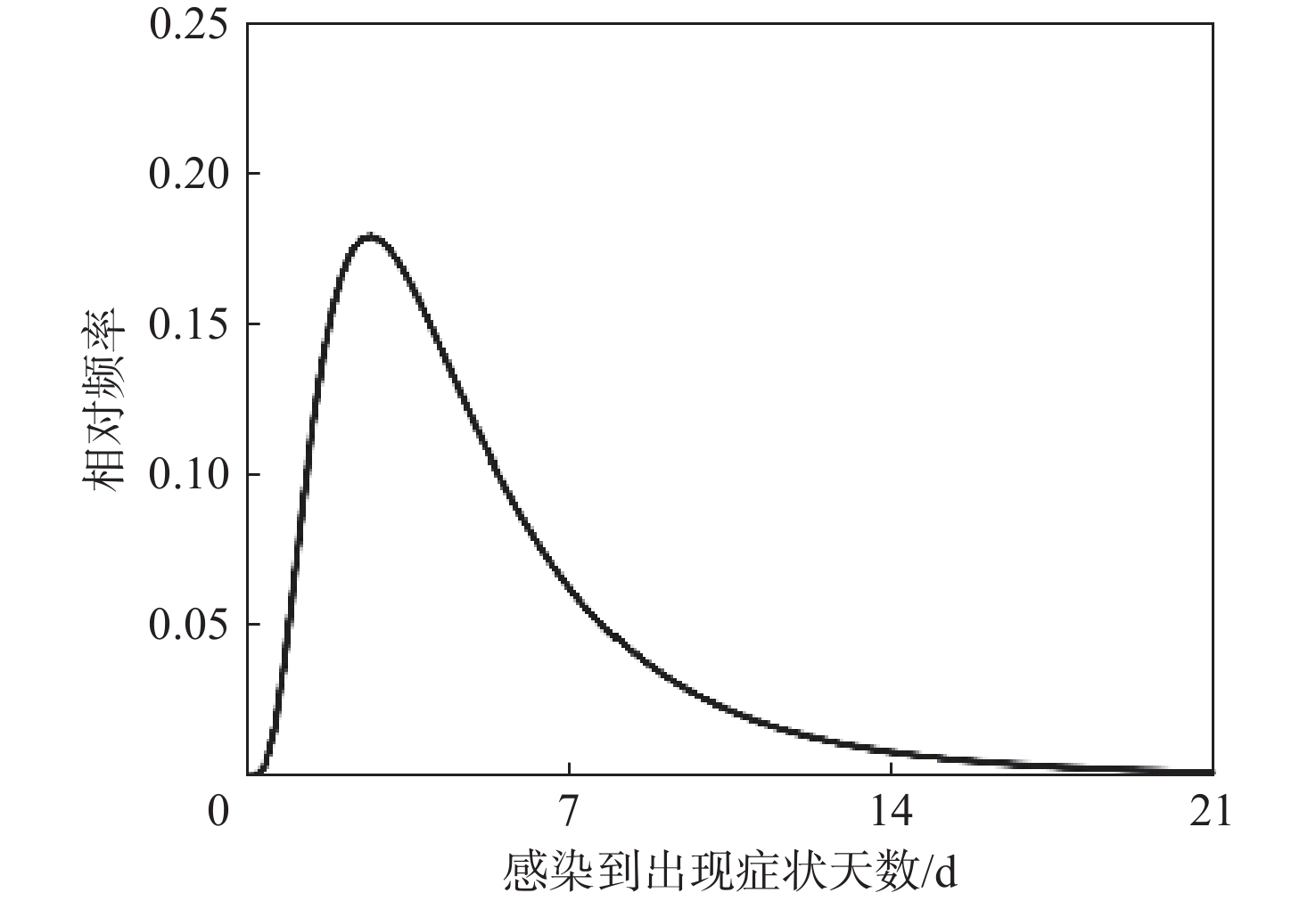
参数 数值 潜伏期泊松分布参数值λ/d 5.5 人人传染率C0 2.7（一级响应前）/ 0.4（一级响应后） 伽马过渡参数值γ 0.9（一级响应前）/ 1.08（一级响应后） 确诊延时T2/d 2 治疗延时T3/d 14 
下载: 导出CSV
表 2 床位投入计算表格
Table 2. Form for calculating bed inputs
日期 床位数/张 医疗单位(列出时间为被指定为
定点医院时间)2019-12-27 842 第1批定点医院* $ \vdots $ 842 2020-01-22 842 2020-01-23 1542 第2批定点医院** 2020-01-24 2142 2020-01-25 2842 2020-01-26 3600 2020-01-27 4313 第3批定点医院*** 2020-01-28 4800 2020-01-29 5300 2020-01-30 5800 2020-01-31 6300 2020-02-01 6754 2020-02-02 7259 2020-02-03 9149 火神山医院 2020-02-04 9204 2020-02-05 9498 2020-02-06 19498 移动方舱 2020-02-07 19498 2020-02-08 21098 雷神山医院 2020-02-09及以后 21098 注：* 第1批定点医院: 武汉市金银潭医院、武汉市肺科医院；** 第2批定点医院: 武汉市汉口医院、武汉市武昌医院、武汉市第五医院、武汉市第七医院、武汉市第九医院、武汉市红十字会医院、武汉市第四医院（西院）、武汉市武钢二医院、武汉市中心医院（后湖） 武汉市第三医院（光谷）；*** 第3批定点医院：同济医院（中法新城）、武汉市协和西院、湖北省人民医院（东院）、湖北省中西医结合医院、武汉科技大学天佑医院、武汉市第六医院、武汉市中医医院（汉阳）、湖北六七二中西医结合骨科医院、武汉市黄陂区中医医院、武汉市江夏区中医医院、武汉市新洲区中医医院、武汉紫荆医院、武汉市汉南区中医医院、武汉市蔡甸区妇幼保健院、解放军中部战区总医院。
下载: 导出CSV
-
[1] 范如国, 王奕博, 罗明, 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析[J]. 电子科技大学学报, 2020, 49(3): 369-374.FAN R G, WANG Y B, LUO M, et al. SEIR-based COVID-19 transmission model and inflection point prediction analysis[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(3): 369-374(in Chinese). [2] 胡云鹤, 孔京, 杨路, 等. 动态增长率模型与海外新冠疫情分析[J]. 应用数学学报, 2020, 43(2): 452-467.HU Y H, KONG J, YANG L, et al. A dynamic growth rate model and its application in global COVID-19 epidemic analysis[J]. Acta Mathematicae Applicatae Sinica, 2020, 43(2): 452-467(in Chinese). [3] 盛华雄, 吴琳, 肖长亮. 新冠肺炎疫情传播建模分析与预测[J]. 系统仿真学报, 2020, 32(5): 759-766.SHENG H X, WU L, XIAO C L. Modeling analysis and prediction on NCP epidemic transmission[J]. Journal of System Simulation, 2020, 32(5): 759-766(in Chinese). [4] 严阅, 陈瑜, 刘可伋, 等. 基于一类时滞动力学系统对新型冠状病毒肺炎疫情的建模和预测[J]. 中国科学: 数学, 2020, 50(3): 385-392. doi: 10.1360/SSM-2020-0026YAN Y, CHEN Y, LIU K J, et al. Modeling and prediction for the trend of outbreak of NCP based on a time-delay dynamic system[J]. Scientia Sinica (Mathematica), 2020, 50(3): 385-392(in Chinese). doi: 10.1360/SSM-2020-0026 [5] ANNAS S, ISBAR PRATAMA M, RIFANDI M, et al. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia[J]. Chaos, Solitons & Fractals, 2020, 139: 110072. [6] HE S B, PENG Y X, SUN K H. SEIR modeling of the COVID-19 and its dynamics[J]. Nonlinear Dynamics, 2020, 101(3): 1667-1680. doi: 10.1007/s11071-020-05743-y [7] LI M T, SUN G Q, ZHANG J, et al. Analysis of COVID-19 transmission in Shanxi Province with discrete time imported cases[J]. Mathematical Biosciences and Engineering, 2020, 17(4): 3710-3720. doi: 10.3934/mbe.2020208 [8] LIU Z H, MAGAL P, SEYDI O, et al. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data[J]. Mathematical Biosciences and Engineering, 2020, 17(4): 3040-3051. doi: 10.3934/mbe.2020172 [9] REZAPOUR S, MOHAMMADI H, SAMEI M E. SEIR epidemic model for covid-19 transmission by Caputo derivative of fractional order[J]. Advances in Difference Equations, 2020(1): 490. [10] YANG C Y, WANG J. A mathematical model for the novel coronavirus epidemic in Wuhan, China[J]. Mathematical Biosciences and Engineering, 2020, 17(3): 2708-2724. doi: 10.3934/mbe.2020148 [11] ZHANG Z Z, ZEB A, HUSSAIN S, et al. Dynamics of COVID-19 mathematical model with stochastic perturbation[J]. Advances in Difference Equations, 2020(1): 451. [12] 赵序茅, 李欣海, 聂常虹. 基于大数据回溯新冠肺炎的扩散趋势及中国对疫情的控制研究[J]. 中国科学院院刊, 2020, 35(3): 248-255.ZHAO X M, LI X H, NIE C H. Backtracking transmission of COVID-19 in China based on big data source, and effect of strict pandemic control policy[J]. Bulletin of Chinese Academy of Sciences, 2020, 35(3): 248-255(in Chinese). [13] 王志心, 刘治, 刘兆军. 基于机器学习的新型冠状病毒(COVID-19)疫情分析及预测[J]. 生物医学工程研究, 2020, 39(1): 1-5.WANG Z X, LIU Z, LIU Z J. COVID-19 analysis and forecast based on machine learning[J]. Journal of Biomedical Engineering Research, 2020, 39(1): 1-5(in Chinese). [14] MALEKI M, MAHMOUDI M R, WRAITH D, et al. Time series modelling to forecast the confirmed and recovered cases of COVID-19[J]. Travel Medicine and Infectious Disease, 2020, 37: 101742. doi: 10.1016/j.tmaid.2020.101742 [15] WANG P P, ZHENG X Q, LI J Y, et al. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics[J]. Chaos, Solitons & Fractals, 2020, 139: 110058. [16] LI Q, GUAN X H, WU P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia[J]. New England Journal of Medicine, 2020, 382(13): 1199-1207. doi: 10.1056/NEJMoa2001316 [17] HE Z Y, REN L L, YANG J T, et al. Seroprevalence and humoral immune durability of anti-SARS-CoV-2 antibodies in Wuhan, China: a longitudinal, population-level, cross-sectional study[J]. Lancet, 2021, 397(10279): 1075-1084. doi: 10.1016/S0140-6736(21)00238-5 [18] STRUGNELL R, WANG N. Sustained neutralising antibodies in the Wuhan population suggest durable protection against SARS-CoV-2[J]. Lancet, 2021, 397(10279): 1037-1039. doi: 10.1016/S0140-6736(21)00434-7 -
下载:
点击查看大图
计量
- 文章访问数: 263
- HTML全文浏览量: 85
- PDF下载量: 4
- 被引次数: 0
