具有同时到达约束的多无人机任务规划

任斯远; 王松; 陈功; 邓晨; 潘正宵

doi:10.13700/j.bh.1001-5965.2023.0783

具有同时到达约束的多无人机任务规划

doi: 10.13700/j.bh.1001-5965.2023.0783

任斯远^{1, 2},
王松^{1, 2},
陈功^{1, 2, ,},
邓晨^{1, 2},
潘正宵^{1, 2}

1.
成都流体动力创新中心，成都 610072
2.
成都智能空中无人系统创新中心，成都 610072

详细信息

通讯作者:
E-mail：success850012@163.com

中图分类号: V221.92；TB553
计量
- 文章访问数: 532
- HTML全文浏览量: 121
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2023-12-01
- 录用日期: 2024-01-26
- 网络出版日期: 2024-02-26
- 整期出版日期: 2026-02-28

Task planning of multiple UAVs with simultaneous arrival constraints

REN Siyuan^{1, 2},
WANG Song^{1, 2},
CHEN Gong^{1, 2
, ,},
DENG Chen^{1, 2},
PAN Zhengxiao^{1, 2}

1.
Chengdu Fluid Dynamics Innovation Center，Chengdu 610072，China
2.
Chengdu Innovation Center for Intelligent Unnanned Aerial System，Chengdu 610072，China

More Information

Corresponding author: E-mail：success850012@163.com

摘要

摘要:
针对无人机(UAV)集群执行任务的问题，考虑无人机任务分配和航迹规划相互耦合的特性及禁飞区约束，提出一种能使无人机群以最短时间同时到达目标位置的任务规划算法。该算法通过Dubins曲线规划路径，使用引入粒子群变异的改进粒子群优化(PSO)算法对任务分配方案进行优化；采用“盘旋等待+动态速度调整”的方法同步各无人机到达目标时间；在基于无人机六自由度动力学模型和动态逆控制模型的仿真环境中对所提算法有效性进行评估验证。仿真结果表明：相比传统PSO算法，改进的PSO算法能够有效跳出局部最优，获得更优的分配方案；在所提算法的控制下，多无人机间飞行时间最大偏差仅有0.5%，满足饱和打击要求。
- 多无人机 /
- 粒子群优化算法 /
- 同时到达 /
- 航迹规划 /
- 航迹跟踪 /
- Dubins曲线
Abstract:
This paper addresses the problem of task execution for unmanned aerial vehicles (UAV) swarms, considering the coupling characteristics of UAV task allocation and trajectory planning as well as the no-fly zone constraints. A task planning algorithm is proposed that can make the UAV swarm reach the target positions in the shortest time simultaneously. A "hovering waiting and dynamic speed adjustment" method is used to synchronize the arrival time of each UAV, Dubins curves are used to design the pathways, and an upgraded particle swarm optimization (PSO) algorithm with particle swarm mutation is used to optimize the task allocation scheme. Finally, the effectiveness of the algorithm is evaluated and verified in a simulation environment based on the six-degree-of-freedom dynamics model and the dynamic inverse control model. In contrast to the conventional PSO algorithm approach, the simulation results demonstrate that this enhanced PSO algorithm is capable of successfully escaping the local optimum and achieving a better allocation scheme. Under the control of the proposed algorithm, the maximum deviation of flight time among multiple UAVs is only 0.5%, meeting the requirements of a saturation attack.
- unmanned aerial vehicles /
- particle swarm optimization algorithm /
- simultaneous arrival /
- route plan /
- route track /
- Dubins curves

HTML全文

图 1 任务规划策略流程图

Figure 1. Flow chart of trajectory control strategy

下载: 全尺寸图片幻灯片

图 2 最优Dubins曲线生成步骤

Figure 2. Steps for generating optimal Dubins curves

下载: 全尺寸图片幻灯片

图 3 带障碍圆Dubins曲线 LSR-SR

Figure 3. Dubins curves with obstacle circles LSR-SR

下载: 全尺寸图片幻灯片

图 4 改进PSO算法流程

Figure 4. Process of improved PSO algorithm

下载: 全尺寸图片幻灯片

图 5 14架无人机从不同方向攻击目标集群

Figure 5. Colony with 14 UAVS attack target clusters from different directions

下载: 全尺寸图片幻灯片

图 6 改进PSO算法20次模拟结果

Figure 6. Results from 20 iterations simulation results of improved PSO algorithm

下载: 全尺寸图片幻灯片

图 7 原始PSO算法20次模拟结果

Figure 7. Simulation results of original PSO algorithm after 20 iterations

下载: 全尺寸图片幻灯片

图 8 改进PSO算法计算性能分析结果

Figure 8. Improved PSO algorithm computational performance analysis results

下载: 全尺寸图片幻灯片

图 9 原始PSO算法计算性能分析结果

Figure 9. Original PSO algorithm computational performance analysis results

下载: 全尺寸图片幻灯片

图 10 增加转弯半径方法调整无人机路径

Figure 10. Adjusting path of UAVs by increasing turning radius

下载: 全尺寸图片幻灯片

图 11 盘旋方法调整无人机路径

Figure 11. Adjusting path of UAVs by hovering

下载: 全尺寸图片幻灯片

图 12 可视化飞行仿真结果

Figure 12. Visualize flight simulation results

下载: 全尺寸图片幻灯片

图 13 高度指令跟踪结果

Figure 13. Height command tracking result

下载: 全尺寸图片幻灯片

图 14 水平轨迹跟踪结果

Figure 14. Horizontal trajectory tracking result

下载: 全尺寸图片幻灯片

表 1 粒子特征信息矩阵P

Table 1. Particle feature information matrix P

目标	P的元素
目标	无人机I	无人机II	无人机III	留空
目标I	0	0	1	0
目标II	1	0	0	0
目标III	0	1	0	0
目标IV	0	0	0	1

下载: 导出CSV

表 2 改进PSO算法的效果

Table 2. Effects of improved PSO algorithm

算法	陷入局部最优次数	进入更优平均迭代次数
改进PSO	0	3.35
原始PSO	7	2.54

下载: 导出CSV

表 3 调整前后路径长度对比

Table 3. Comparison of path length before and after adjustment

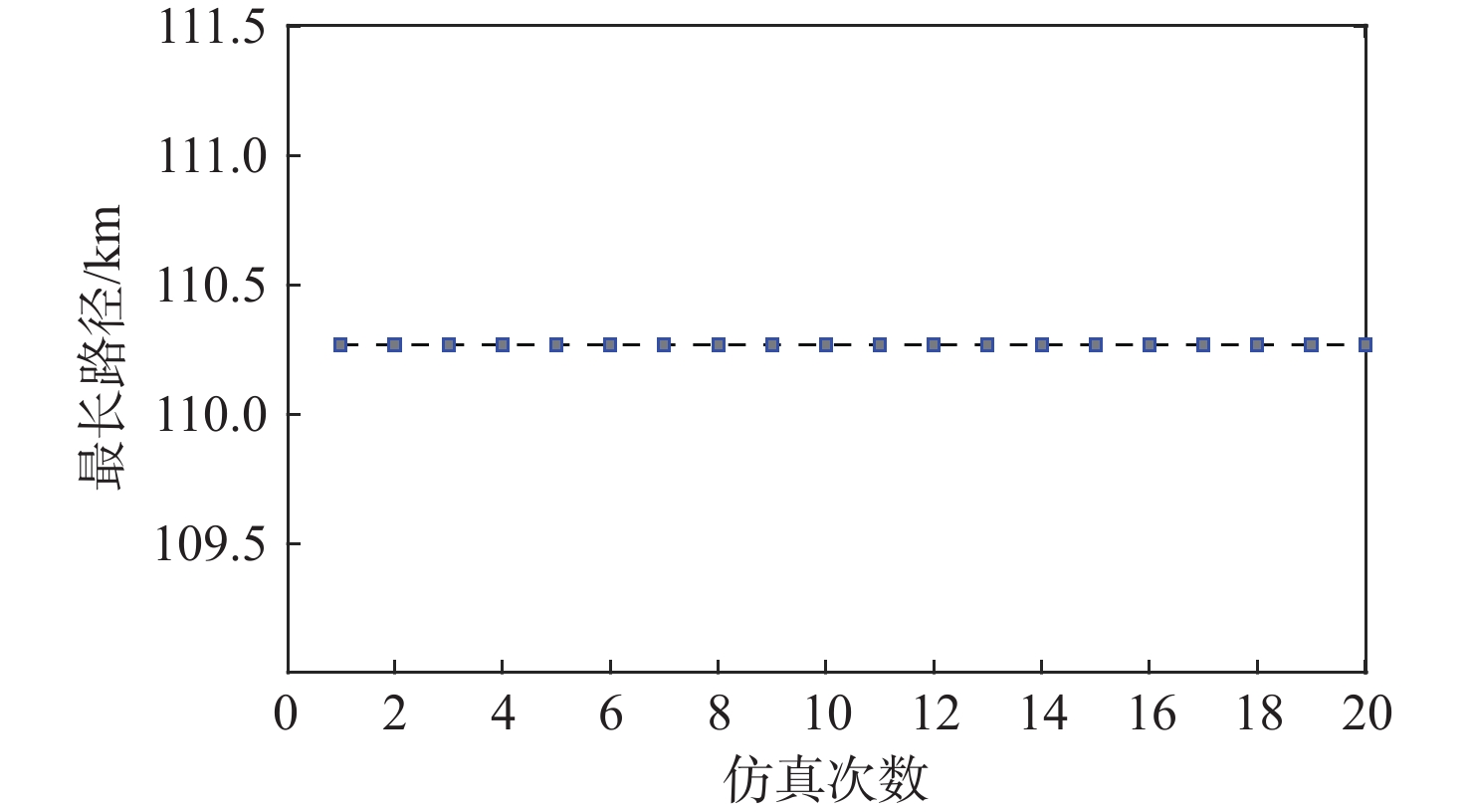
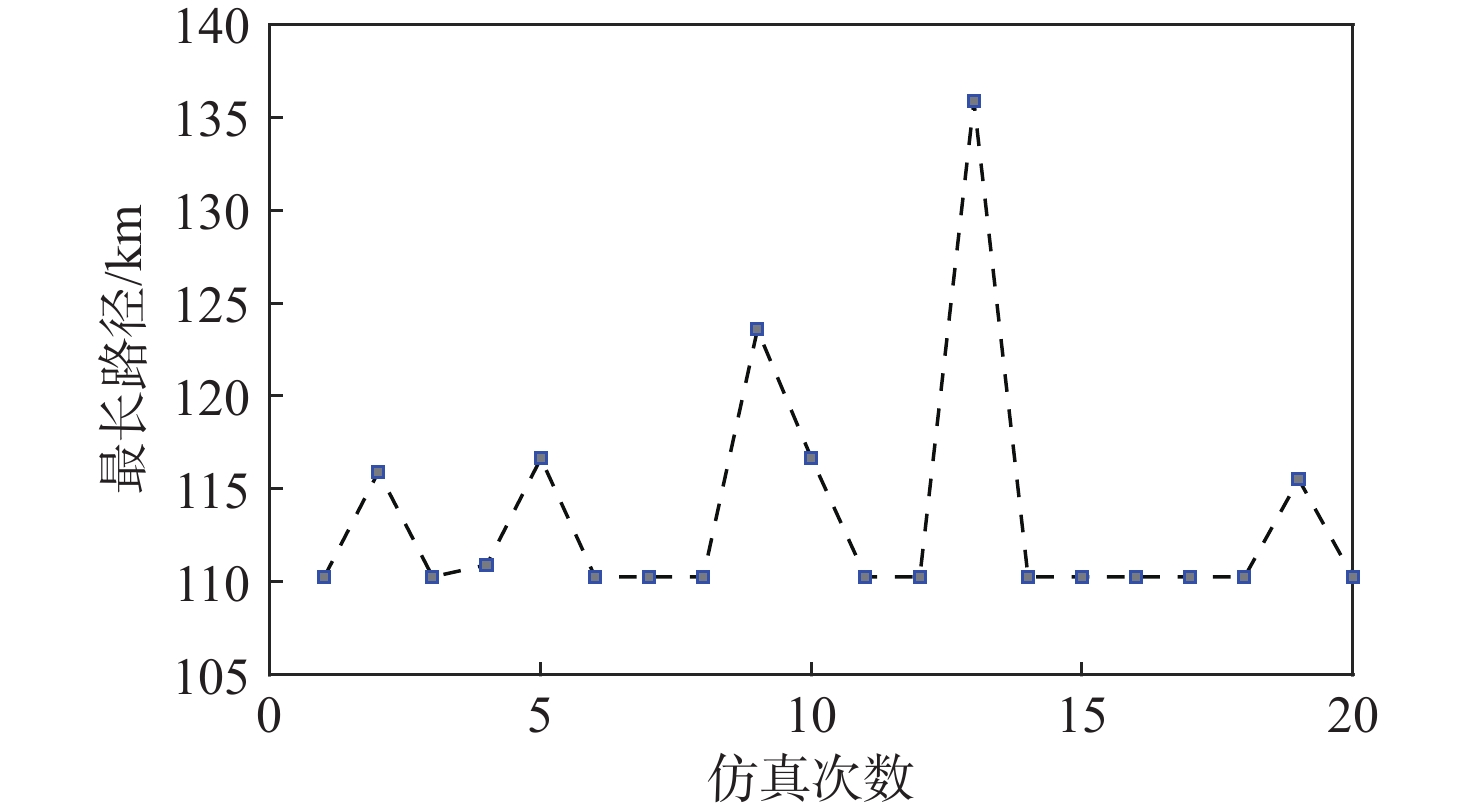
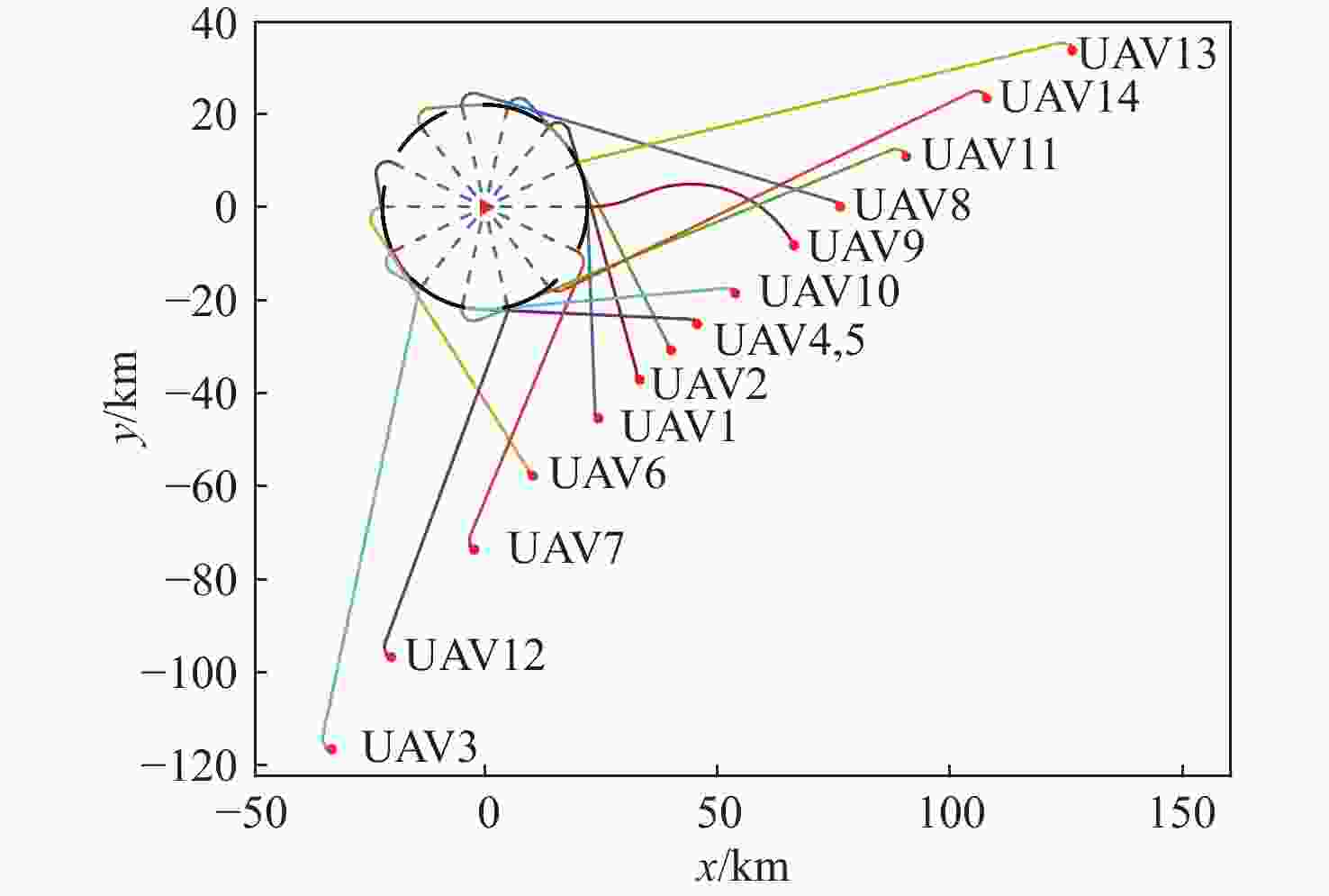
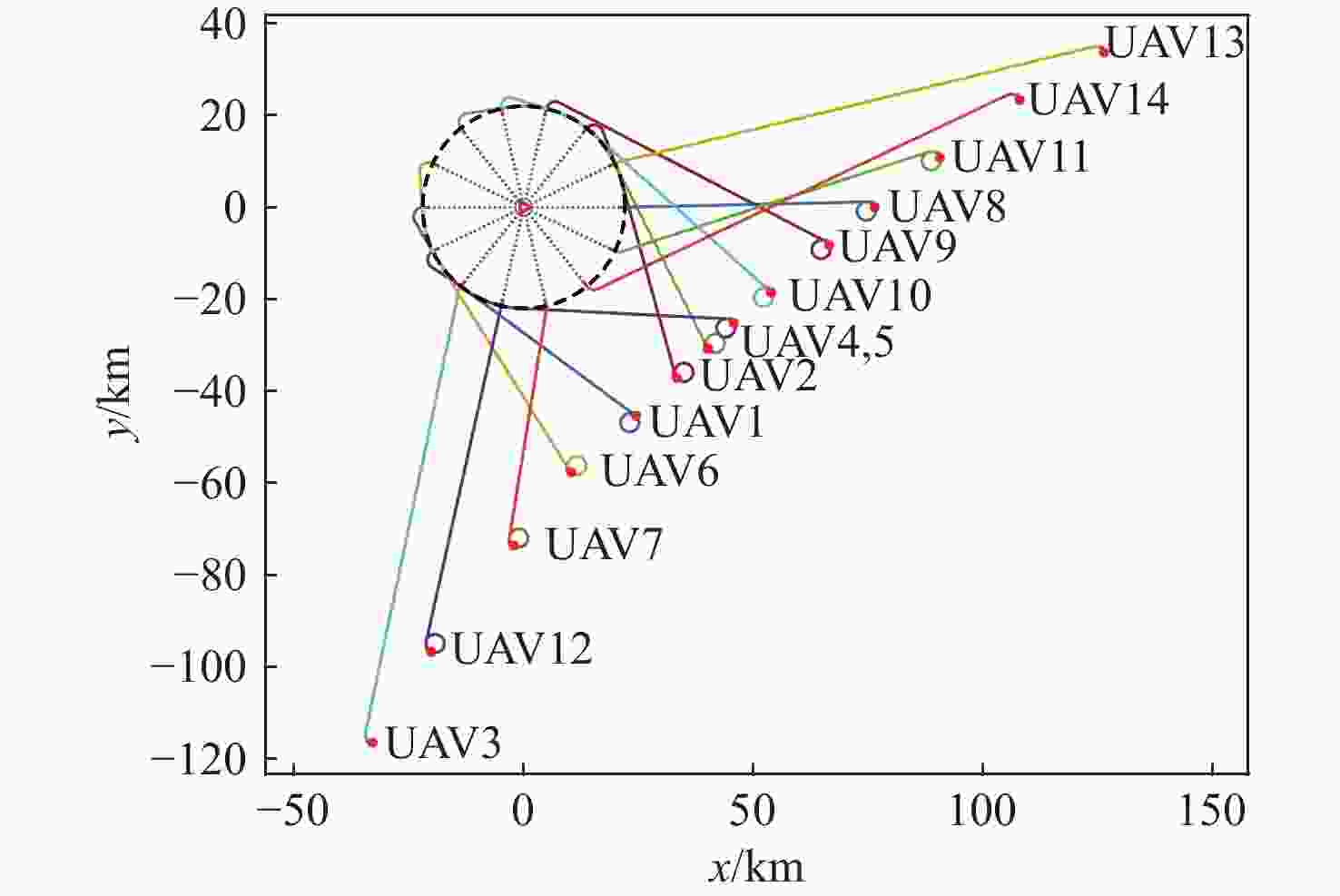
无人机序号	原始路径长度/km	增加转弯半径后路径长度/km	盘旋后路径长度/km
1	77.90070	77.90070	109.3166
2	61.08414	61.08414	108.2080
3	102.60840	102.60840	102.6084
4	87.17995	87.17995	102.8879
5	93.09158	93.09158	108.7995
6	69.29088	69.29088	100.7068
7	69.87339	69.87339	101.2893
8	87.24825	87.24825	102.9562
9	45.50841	50.05252	108.3403
10	81.65244	81.65244	97.3604
11	105.50630	105.50630	105.5063
12	80.63224	80.63224	96.3402
13	110.26840	110.26840	110.2684
14	105.00500	105.00500	105.0050

下载: 导出CSV

表 4 各无人机飞行时间

Table 4. Flight time of each UAV

无人机序号	到达时间/s	无人机序号	到达时间/s
1	2247	8	2247
2	2248	9	2244
3	2246	10	2245
4	2247	11	2240
5	2245	12	2239
6	2243	13	2239
7	2237	14	2242

下载: 导出CSV

参考文献(17)

[1]	KIM H G, KIM H J. Backstepping-based impact time control guidance law for missiles with reduced seeker field-of-view[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(1): 82-94. doi: 10.1109/TAES.2018.2848319
[2]	ZENG J, DOU L H, XIN B. A joint mid-course and terminal course cooperative guidance law for multi-missile salvo attack[J]. Chinese Journal of Aeronautics, 2018, 31(6): 1311-1326. doi: 10.1016/j.cja.2018.03.016
[3]	ZHEN Z Y, XING D J, GAO C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm[J]. Aerospace Science and Technology, 2018, 76: 402-411. doi: 10.1016/j.ast.2018.01.035
[4]	BEARD R W, MCLAIN T W, GOODRICH M A, et al. Coordinated target assignment and intercept for unmanned air vehicles[J]. IEEE Transactions on Robotics and Automation, 2002, 18(6): 911-922. doi: 10.1109/TRA.2002.805653
[5]	沈林成, 陈璟, 王楠. 飞行器任务规划技术综述[J]. 航空学报, 2014, 35(3): 593-606. SHEN L C, CHEN J, WANG N. Overview of air vehicle mission planning techniques[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 593-606(in Chinese).
[6]	DOBROKHODOV V. Cooperative path planning of unmanned aerial vehicles[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(5): 1601-1602. doi: 10.2514/1.54851
[7]	SHIMA T, RASMUSSEN S, GROSS D. Assigning micro UAVs to task tours in an urban terrain[J]. IEEE Transactions on Control Systems Technology, 2007, 15(4): 601-612. doi: 10.1109/TCST.2007.899154
[8]	梁勇, 张友安, 雷军委. 一种基于Dubins路径的在线快速航路规划方法[J]. 系统仿真学报, 2013, 25(S1): 291-296. LIANG Y, ZHANG Y A, LEI J W. New method of online fast path planning based dubins path[J]. Journal of System Simulation, 2013, 25(S1): 291-296(in Chinese).
[9]	刘流, 梁晓龙, 何吕龙, 等. 考虑速度约束的无人机Dubins路径规划[J]. 火力与指挥控制, 2018, 43(12): 50-54. LIU L, LIANG X L, HE L L, et al. Dubins path planning of UAV considering velocity constraint[J]. Fire Control & Command Control, 2018, 43(12): 50-54(in Chinese).
[10]	陈清阳, 辛宏博, 王玉杰, 等. 一种多机协同打击的快速航迹规划方法[J]. 北京航空航天大学学报, 2022, 48(7): 1145-1153. CHEN Q Y, XIN H B, WANG Y J, et al. A rapid path planning method for multiple UAVs to cooperative strike[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(7): 1145-1153(in Chinese).
[11]	王红勇, 郭宇鹏. 终端区离场航空器自主路径规划[J]. 北京航空航天大学学报, 2025, 51(2): 446-456. WANG H Y, GUO Y P. Autonomous path planning of departing aircraft in terminal area[J]. Journal of Beijing University of Aeronautics and Astronautics, 2025, 51(2): 446-456(in Chinese).
[12]	韩维, 司维超, 丁大春, 等. 基于聚类PSO算法的舰载机舰面多路径动态规划[J]. 北京航空航天大学学报, 2013, 39(5): 610-614. HAN W, SI W C, DING D C, et al. Multi-routes dynamic planning on deck of carrier plane based on clustering PSO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 610-614(in Chinese).
[13]	严飞, 祝小平, 周洲, 等. 考虑同时攻击约束的多异构无人机实时任务分配[J]. 中国科学: 信息科学, 2019, 49(5): 555-569. doi: 10.1360/N112018-00338 YAN F, ZHU X P, ZHOU Z, et al. Real-time task allocation for a heterogeneous multi-UAV simultaneous attack[J]. Scientia Sinica (Informationis), 2019, 49(5): 555-569(in Chinese). doi: 10.1360/N112018-00338
[14]	蒋硕, 袁小平. 改进PSO算法在多无人机协同任务分配中的应用[J]. 计算机应用研究, 2019, 36(11): 3344-3347. JIANG S, YUAN X P. Application of improved PSO algorithm in multi UAV cooperative task allocation[J]. Application Research of Computers, 2019, 36(11): 3344-3347(in Chinese).
[15]	BARSKY B A, DEROSE T D. Geometric continuity of parametric curves: three equivalent characterizations[J]. IEEE Computer Graphics and Applications, 1989, 9(6): 60-69. doi: 10.1109/38.41470
[16]	SHANMUGAVEL M. Path planning of multiple autonomous vehicles[D]. Cranfield: Cranfield University, 2007.
[17]	丁海利, 王芳, 高成修. 旅行商问题的交叉粒子群优化算法[J]. 数学杂志, 2008, 28(1): 85-89. DING H L, WANG F, GAO C X. Crossover particle swarm optimization for traveling salesman problem[J]. Journal of Mathematics, 2008, 28(1): 85-89(in Chinese).