-
摘要:
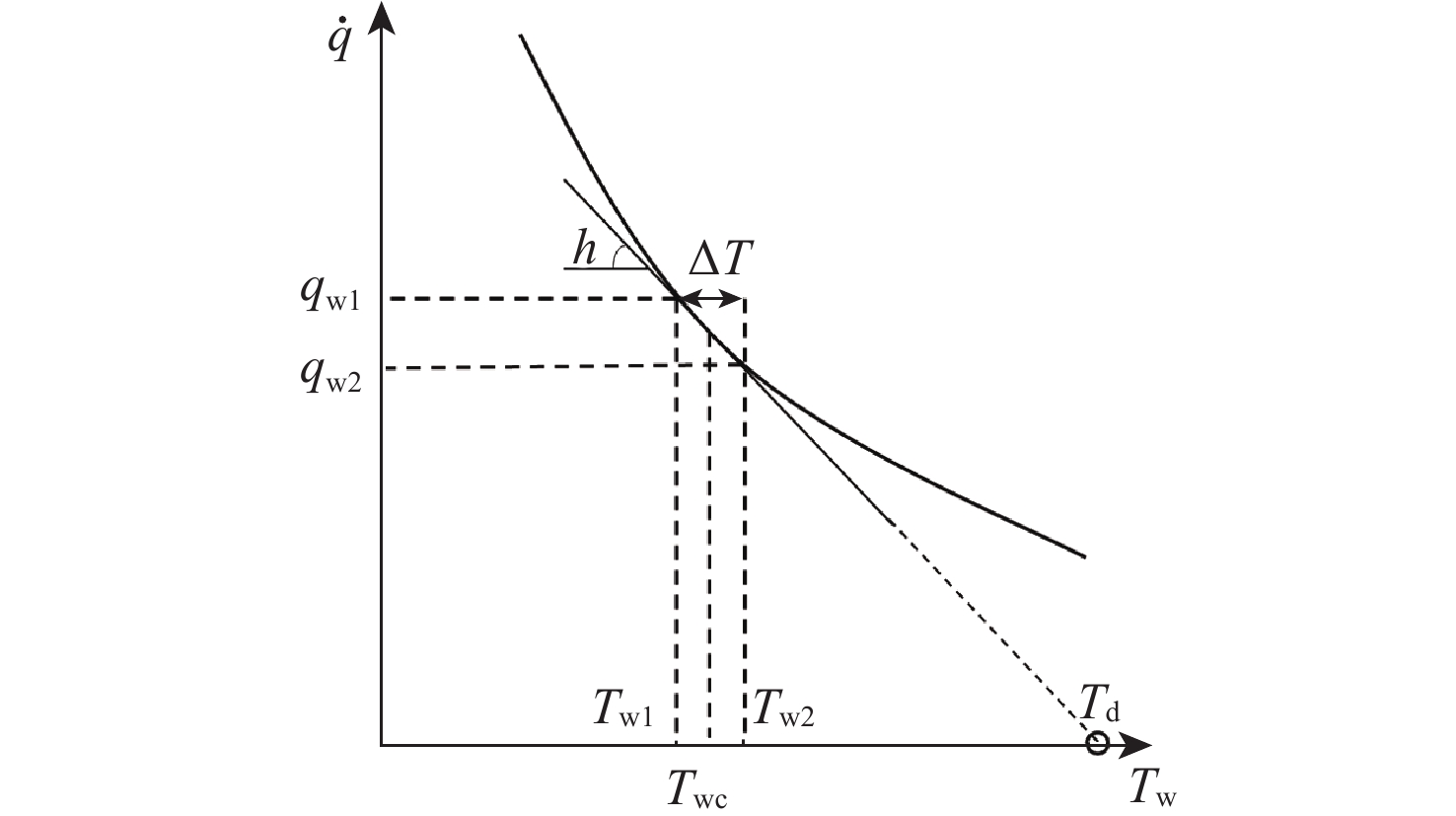
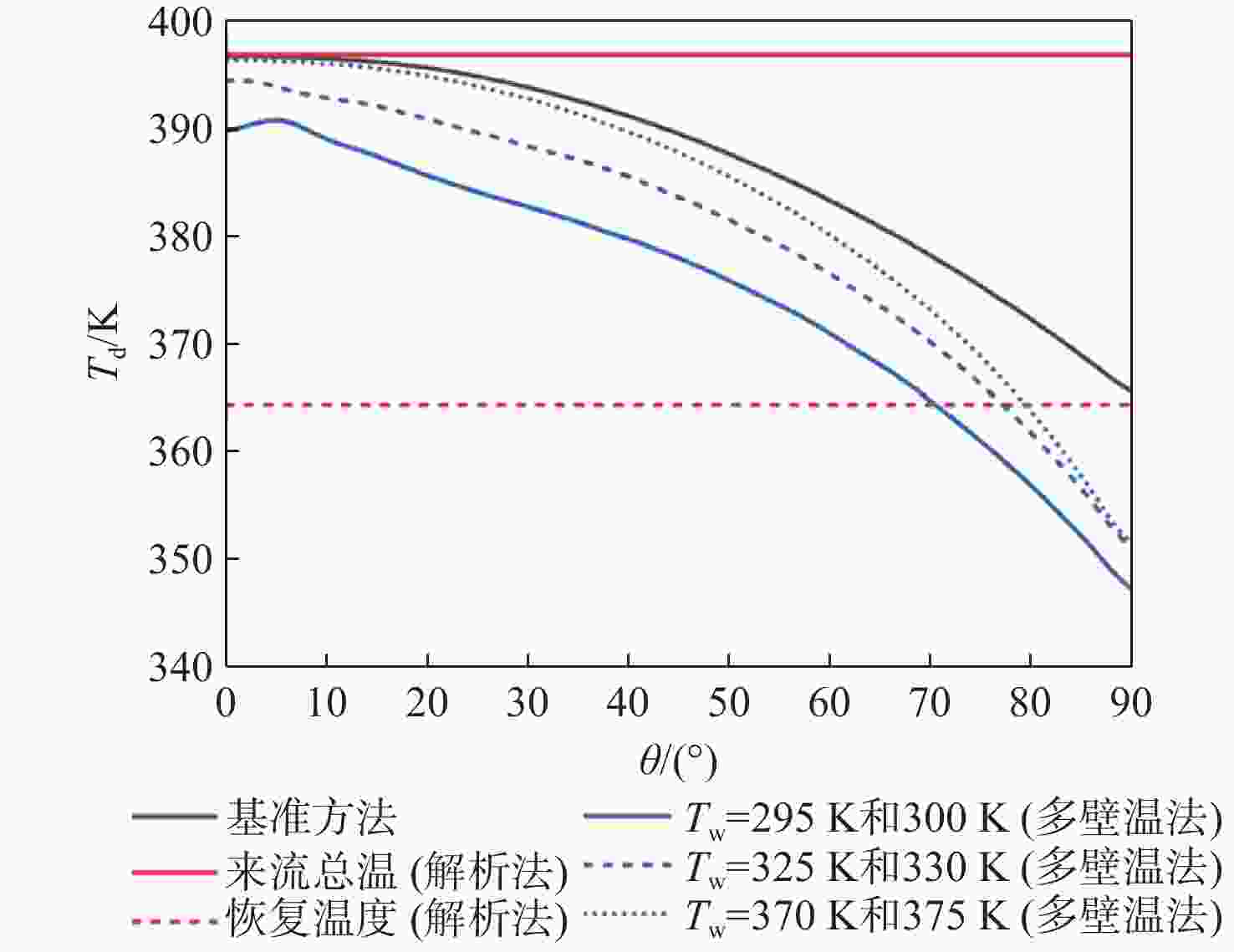
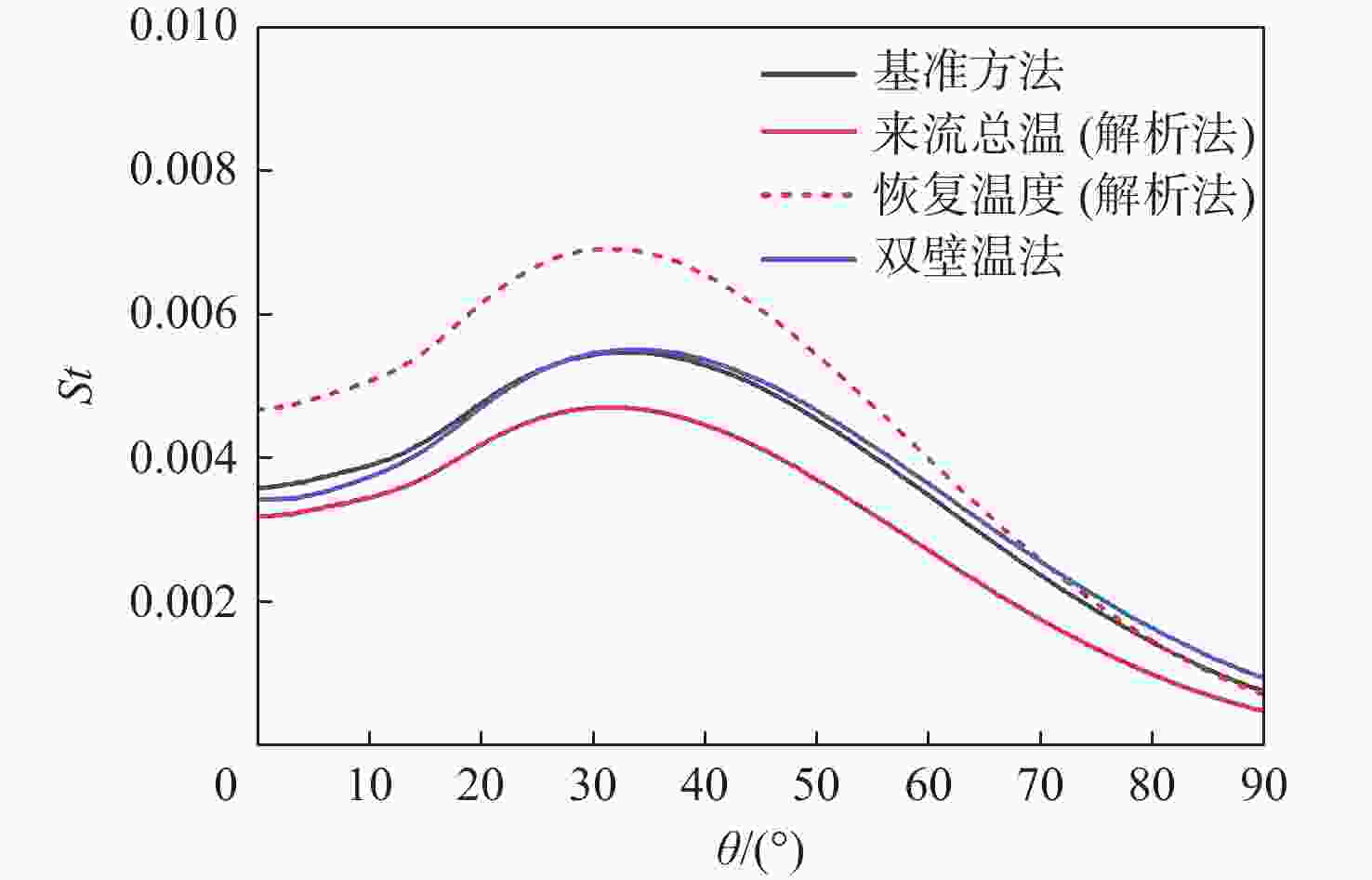
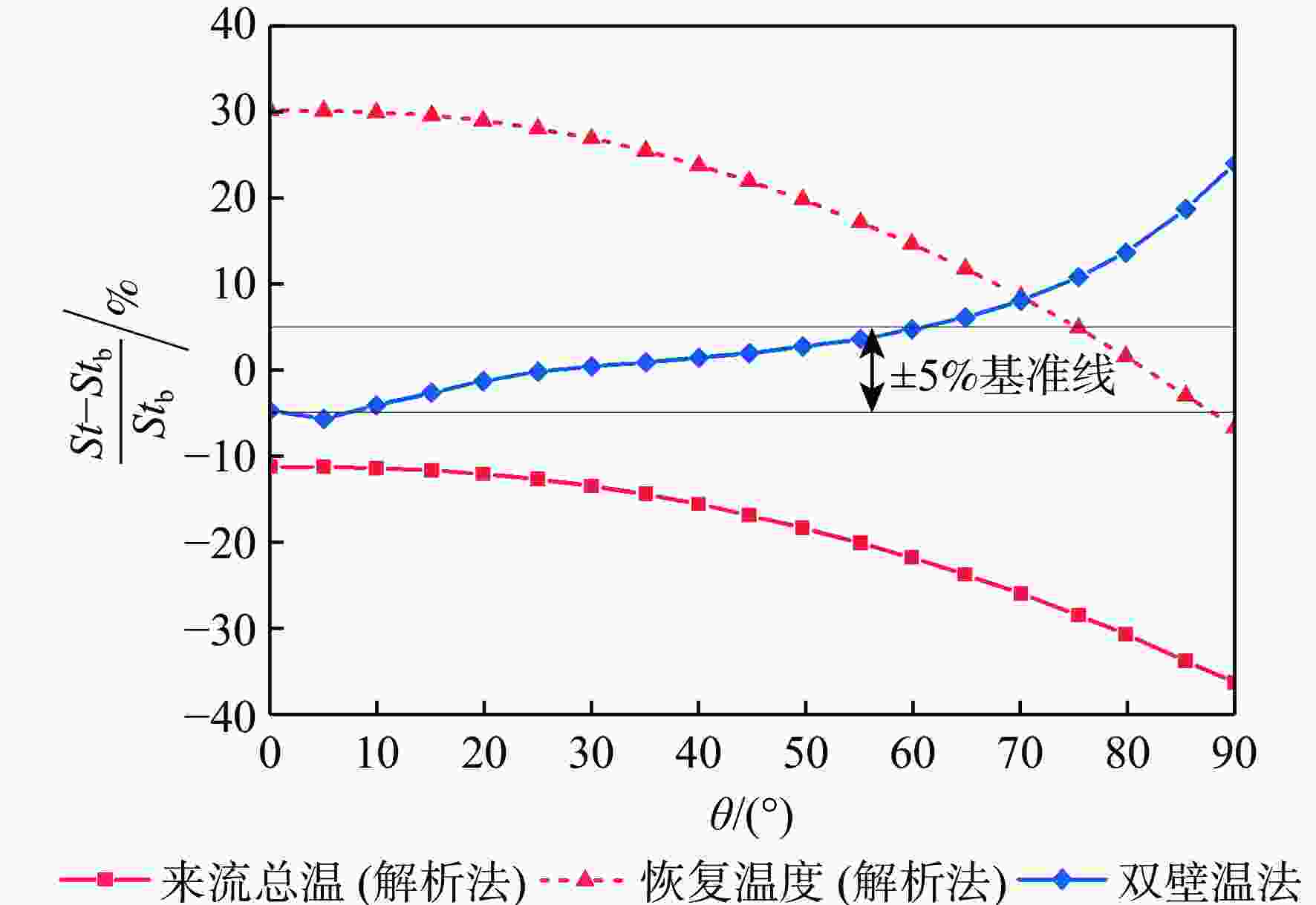
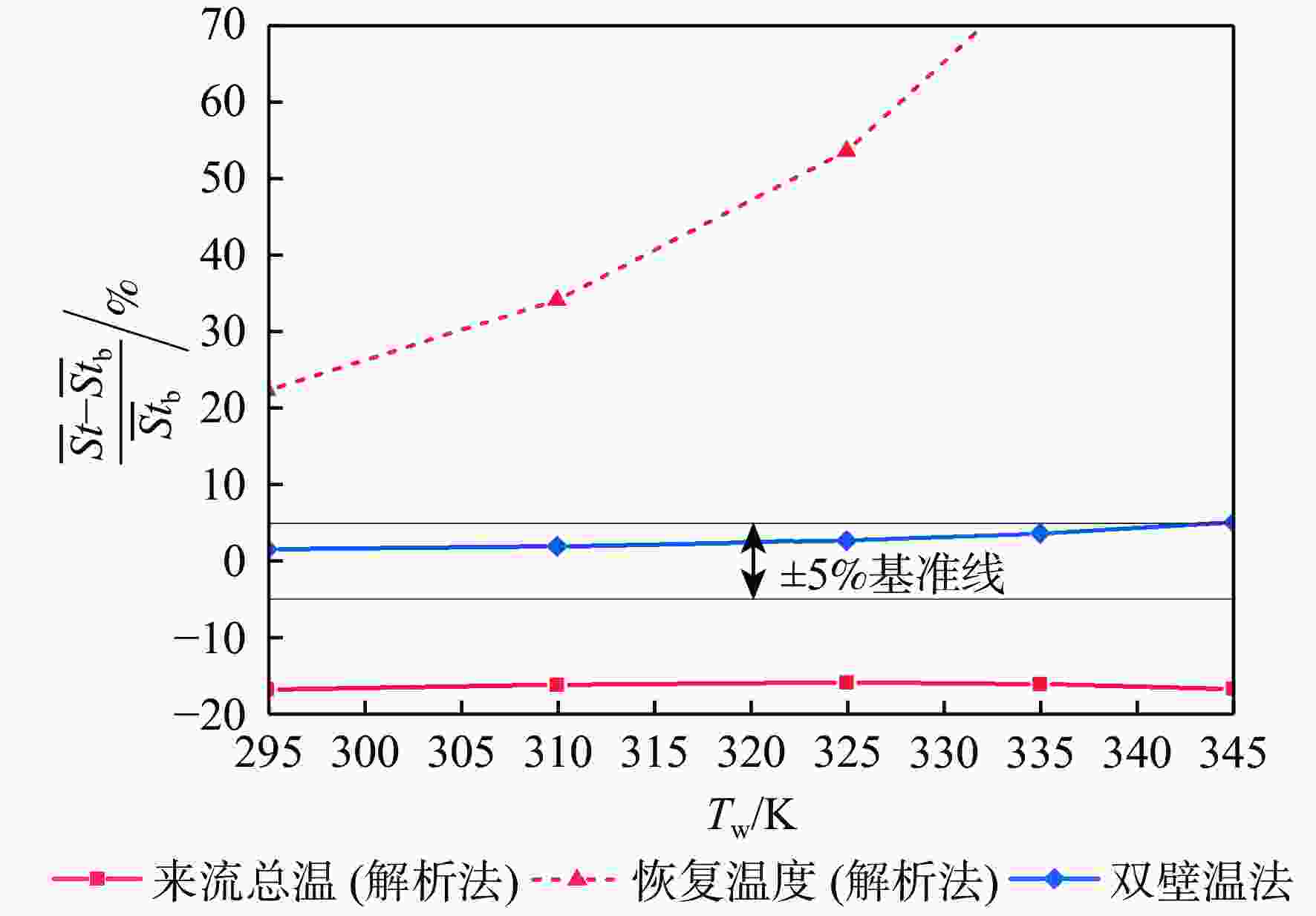
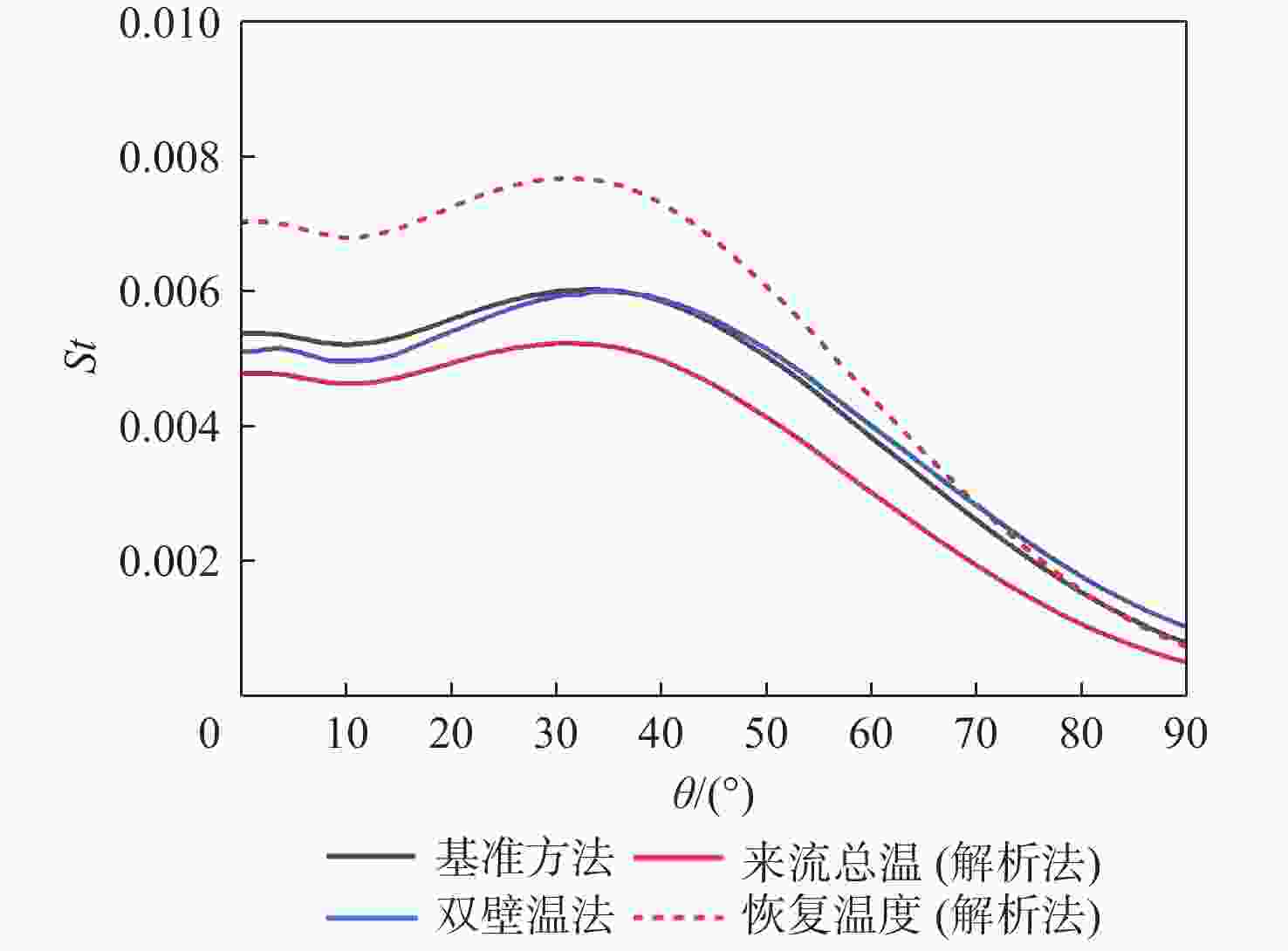
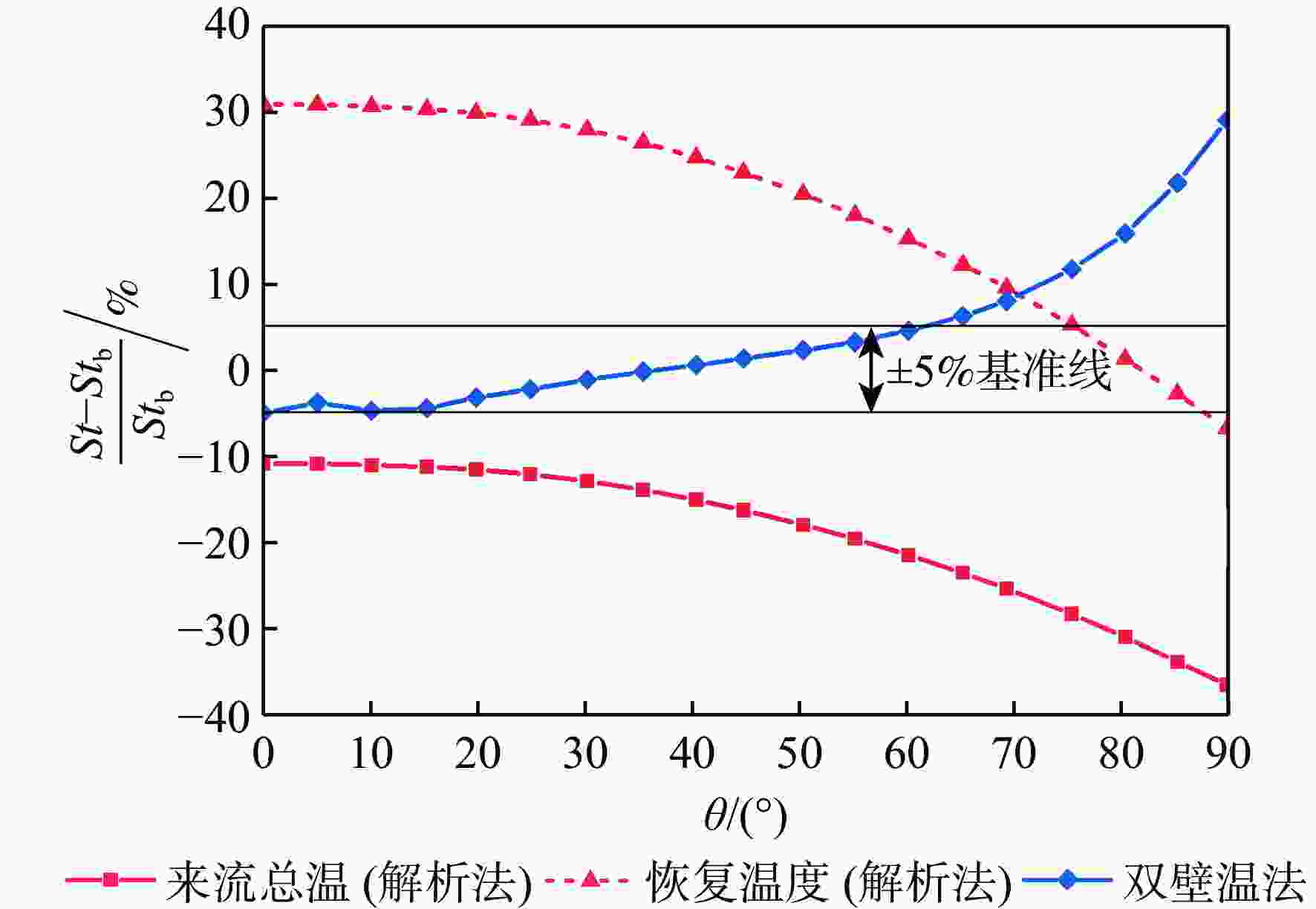
斯坦顿数是评价飞行器气动热性能的重要指标,但其求解方法尚有分歧,主要体现在对流换热驱动温度的确定方式上。当前常用的2种方法均基于解析公式获得驱动温度,统称为“解析法”:第1种方法选取来流总温作为驱动温度,第2种方法选取高速流动外掠平板时的壁面恢复温度作为驱动温度。鉴于此,以驱动温度等于绝热壁温的方法为基准,通过数值仿真对比了上述2种解析法与新引入的双壁温法(即由2组等温壁面算例的结果作差获得对流换热系数)在求解钝体壁面斯坦顿数时的准确性。结果表明:双壁温法所得斯坦顿数与基准方法的吻合度远高于2种解析法,其壁面平均斯坦顿数与基准方法的相对偏差在5%以内,而2种解析法的相对偏差均大于15%。此外,双壁温法所得驱动温度沿钝体圆周角的变化趋势与绝热壁温一致,而2种解析法所得驱动温度在各圆周角下均为定值,不符合物理规律。
Abstract:The Stanton number is an important barometer in evaluating the aerodynamic thermal performance of a vehicle, but its determination is still subject to controversy, particularly because the method for obtaining the driving temperature during the convective heat transfer process is arguable. The two approaches that are frequently used in the open literature are referred to as "analytical methods" because they both use analytical formulas to determine the driving temperature. One considers the driving temperature to be the total temperature of the incoming flow, while the other compares it to the recovery temperature for high-speed flow over a flat plate. To resolve this dispute, this paper conducted numerical simulations to compare the accuracy of the two analytical methods, as well as the newly introduced two-point method (whose convective heat transfer coefficient is obtained by subtracting the results of two isothermal cases with different wall temperatures), in solving the Stanton number on the blunt body. The baseline for comparison is the method where the driving temperature is the adiabatic wall temperature. Numerical results show that the Stanton number calculated by the two-point method provides a much better agreement with the baseline method than the two analytic methods. The difference between the two-point method's area-averaged Stanton number and the baseline method is less than 5%, whereas the difference between the two analytical approaches and the baseline method is more than 15%. Moreover, the driving temperature derived by the two-point method varies along the circumferential angle of the blunt body with the same trend as the adiabatic wall temperature. In contrast, the driving temperature calculated by either of the two analytic methods remains a constant value at different circumferential angles, which does not comply with our physical consensus.
-
Key words:
- supersonic /
- blunt bodies /
- aerodynamic heating /
- Stanton number /
- driving temperature /
- two-point method
-
表 1 流动条件
Table 1. Flow conditions
参数 数值 马赫数 3.98 来流总压/MPa 1.37 来流总温/K 397 壁面温度/K 295/300 单位雷诺数/m−1 4.2×107 表 2 网格独立性研究参数
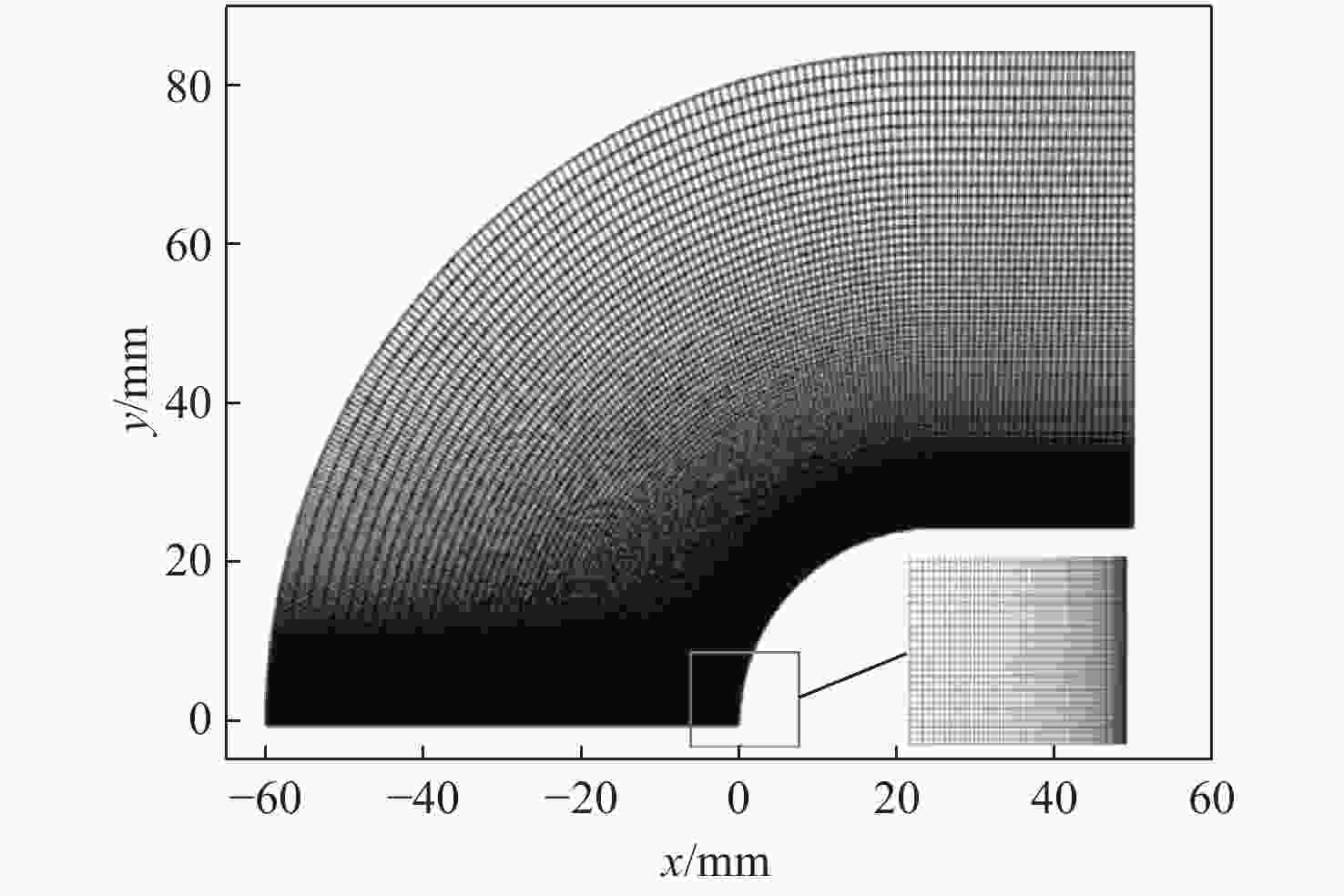
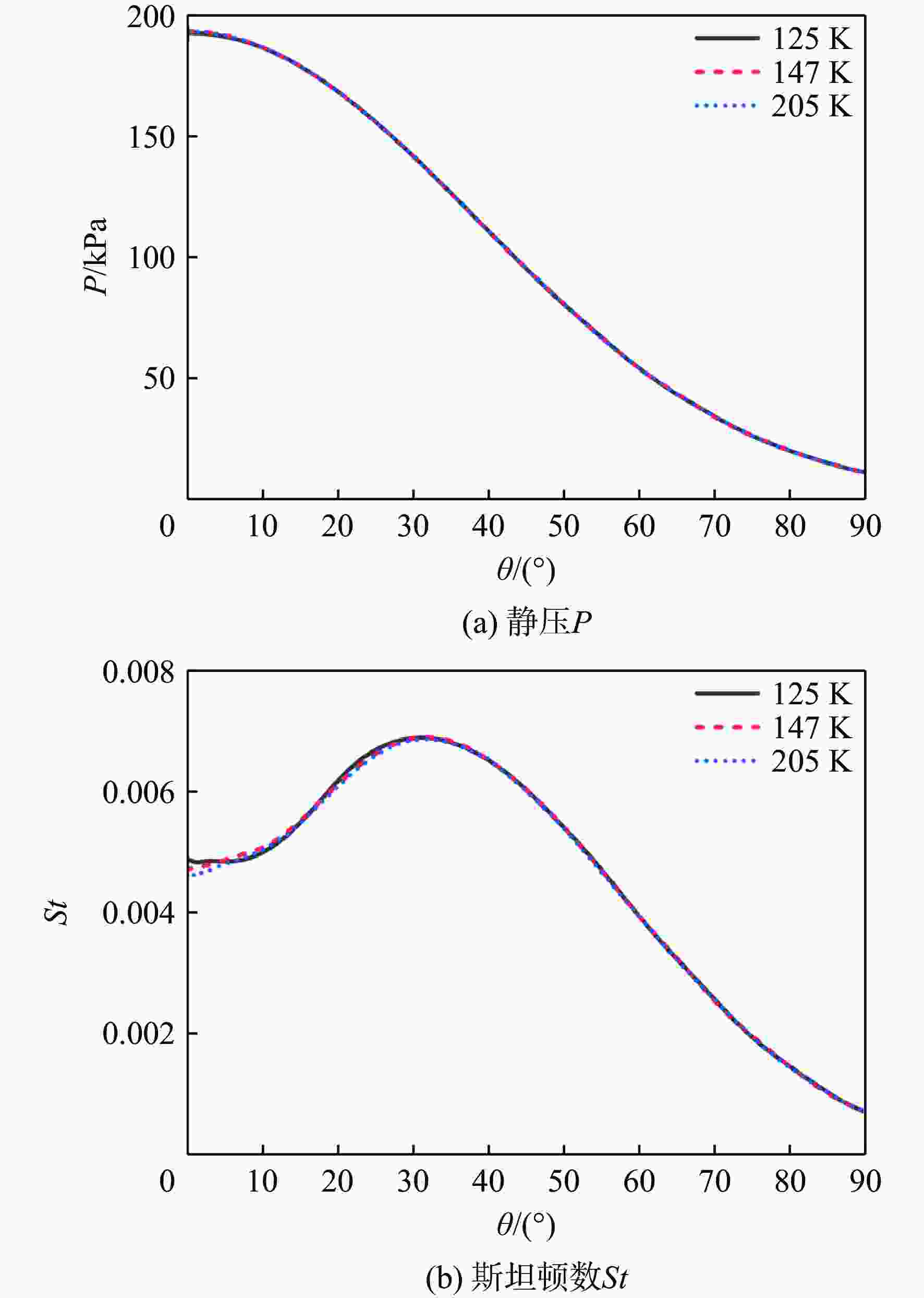
Table 2. Parameters of mesh independence study
网格数 首层网格高度/m 增长率 网格雷诺数 平均斯坦顿数 125 000 4×10−7 1.2 16 0.00 429 147 000 2×10−7 1.1 8 0.00 442 205 000 1×10−7 1.1 4 0.00 441 -
[1] ZHU L, LI Y K, CHEN X, et al. Novel combinational aerodisk and lateral jet concept for drag and heat reduction in hypersonic flows[J]. Journal of Aerospace Engineering, 2019, 32: 04018133. doi: 10.1061/(ASCE)AS.1943-5525.0000966 [2] CHEN F, LIU H, ZHANG S T. Coupled heat transfer and thermo-mechanical behavior of hypersonic cylindrical leading edges[J]. International Journal of Heat and Mass Transfer, 2018, 122: 846-862. doi: 10.1016/j.ijheatmasstransfer.2018.02.037 [3] ZENG K C, XIANG J W, LI D C. Aeroservoelastic modeling and analysis of a canard-configured air-breathing hypersonic vehicles[J]. Chinese Journal of Aeronautics, 2013, 26(4): 831-840. doi: 10.1016/j.cja.2013.06.001 [4] GUO J, HUANG H M, XU X L. Protective effect of pyrolysis gases combustion against surface ablation under different Mach numbers[J]. Acta Astronautica, 2020, 166: 209-217. doi: 10.1016/j.actaastro.2019.10.032 [5] CHANG C L, VENKATACHARI B S, CHENG G. Effect of counterflow jet on a supersonic reentry capsule[C]//Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Berlin: AIAA, 2006: 4776. [6] ASO S, MIYAMOTO Y, KUROTAKI T, et al. Experimental and computational study on reduction of aerodynamic heating load by film cooling in hypersonic flows[C]//Proceedings of the 35th Aerospace Sciences Meeting and Exhibit. Berlin: AIAA, 1997: 770. [7] ZHANG Z K, XU W W, YE W, et al. Heated wind-tunnel experiments and numerical investigations on hypersonic blunt cone aerodynamic heating[J]. Acta Astronautica, 2022, 197: 154-168. doi: 10.1016/j.actaastro.2022.05.021 [8] KULKARNI V, REDDY K P J. Effect of a supersonic counterflow jet on blunt body heat transfer rates for oncoming high enthalpy flow[J]. Journal of Engineering Physics and Thermophysics, 2009, 82(1): 1-5. doi: 10.1007/s10891-009-0173-1 [9] DASO E O, PRITCHETT V E, WANG T S, et al. Dynamics of shock dispersion and interactions in supersonic freestreams with counterflowing jets[J]. AIAA Journal, 2009, 47(6): 1313-1326. doi: 10.2514/1.30084 [10] DECHAUMPHAI P, WIETING A R, THORNTON E A. Flow-thermal-structural study of aerodynamically heated leading edges[J]. Journal of Spacecraft and Rockets, 1989, 26(4): 201-209. doi: 10.2514/3.26055 [11] MENEZES V, SARAVANAN S, JAGADEESH G, et al. Experimental investigations of hypersonic flow over highly blunted cones with aerospikes[J]. AIAA Journal, 2003, 41(10): 1955-1966. doi: 10.2514/2.1885 [12] SAHOO N, KULKARNI V, SARAVANAN S, et al. Film cooling effectiveness on a large angle blunt cone flying at hypersonic speed[J]. Physics of Fluids, 2005, 17(3): 036102. doi: 10.1063/1.1862261 [13] FU J, YI S H, WANG X H, et al. Experimental study on supersonic film cooling on the surface of a blunt body in hypersonic flow[J]. Chinese Physics B, 2014, 23(10): 104702. doi: 10.1088/1674-1056/23/10/104702 [14] HAYASHI K, ASO S, TANI Y. Experimental study on thermal protection system by opposing jet in supersonic flow[J]. Journal of Spacecraft and Rockets, 2006, 43(1): 233-235. doi: 10.2514/1.15332 [15] HAYASHI K, ASO S. Effect of pressure ratio on aerodynamic heating reduction due to opposing jet[C]//Proceedings of the 36th AIAA Thermophysics Conference. Berlin: AIAA, 2003: 4041. [16] DAI S M, MA H T, XU Z R, et al. Numerical study of discrete film cooling near the rudder shaft of a hypersonic air fin model[J]. Numerical Heat Transfer, Part A: Applications, 2024, 85(5): 679-701. doi: 10.1080/10407782.2023.2190939 [17] ZHANG F, YI S H, XU X W, et al. A swept fin-induced flow field with different height mounting gaps[J]. Chinese Journal of Aeronautics, 2021, 34(1): 148-162. doi: 10.1016/j.cja.2020.09.050 [18] HUANG W, JIANG Y P, YAN L, et al. Heat flux reduction mechanism induced by a combinational opposing jet and cavity concept in supersonic flows[J]. Acta Astronautica, 2016, 121: 164-171. doi: 10.1016/j.actaastro.2016.01.008 [19] HUANG W, YAN L, LIU J, et al. Drag and heat reduction mechanism in the combinational opposing jet and acoustic cavity concept for hypersonic vehicles[J]. Aerospace Science and Technology, 2015, 42: 407-414. doi: 10.1016/j.ast.2015.01.029 [20] 郭建, 方蜀州, 王子玉. 高超声速飞行器减阻杆-双盘-槽道组合构型减阻防热特性研究[J]. 推进技术, 2024, 45(5): 89-99.GUO J, FANG S Z, WANG Z Y. Drag and heat flux reduction induced by a novel combinational spike with double aerodisks and channel concept for hypersonic vehicles[J]. Journal of Propulsion Technology, 2024, 45(5): 89-99(in Chinese). [21] 许阳, 陈宣亮. 超声速飞行器减阻杆/盘与双喷流组合构型减阻和防热性能[J]. 航空动力学报, 2024, 39(5): 213-230.XU Y, CHEN X L. Drag and heat flux reduction performance of supersonic vehicle with combination model of aerospike/aerodisk and double jet[J]. Journal of Aerospace Power, 2024, 39(5): 213-230. (in Chinese). [22] 王子玉, 方蜀州, 郭建, 等. 高超声速杆-盘-自耦合冲压横向射流新概念的减阻防热数值模拟[J]. 航空动力学报, 2024, 39(10): 354-366.WANG Z Y, FANG S Z, GUO J, et al. Numerical simulation on drag and heat reduction of hypersonic spike-aerodisk-self-coupled stamping lateral jet concept[J]. Journal of Aerospace Power, 2024, 39(10): 354-366 (in Chinese). [23] MA H, ZHANG Q, HE L, et al. Cooling injection effect on a transonic squealer tip: part I: experimental heat transfer results and CFD validation[J]. Journal of Engineering for Gas Turbines and Power, 2017, 139(5): 052506. doi: 10.1115/1.4035175 [24] MA H T, ZENG W, JIANG H M, et al. Impact of cooling injection on shock wave over a flat tip in high pressure turbine[J]. Journal of Turbomachinery, 2022, 144: 011012. doi: 10.1115/1.4052135 [25] MAFFULLI R, HE L. Wall temperature effects on heat transfer coefficient for high-pressure turbines[J]. Journal of Propulsion and Power, 2014, 30(4): 1080-1090. doi: 10.2514/1.B35126 [26] MAFFULLI R, HE L. Impact of wall temperature on heat transfer coefficient and aerodynamics for three-dimensional turbine blade passage[J]. Journal of Thermal Science and Engineering Applications, 2017, 9(4): 041002. doi: 10.1115/1.4036012 [27] ZHANG C L, CHANG J T, LIU M M, et al. Effect of heat release on movement characteristics of shock train in an isolator[J]. Acta Astronautica, 2017, 133: 185-194. doi: 10.1016/j.actaastro.2017.01.031 [28] HUANG W, ZHANG R R, YAN L, et al. Numerical experiment on the flow field properties of a blunted body with a counterflowing jet in supersonic flows[J]. Acta Astronautica, 2018, 147: 231-240. doi: 10.1016/j.actaastro.2018.04.018 [29] YANG J L, LIU M. A wall grid scale criterion for hypersonic aerodynamic heating calculation[J]. Acta Astronautica, 2017, 136: 137-143. doi: 10.1016/j.actaastro.2016.11.043 [30] BIBI A, MAQSOOD A, SHERBAZ S, et al. Drag reduction of supersonic blunt bodies using opposing jet and nozzle geometric variations[J]. Aerospace Science and Technology, 2017, 69: 244-256. doi: 10.1016/j.ast.2017.06.007 [31] KAYS W M, CRAWFORD M E, WEIGAND B, et al. Convective heat and mass transfer[J]. Prandtl’s Essentials of Fluid Mechanics, 1980, 158: 427-452. -






 下载:
下载: