Active obstacle avoidance based on an improved dynamic window approach for off-axis full trailer vehicles
-
摘要:
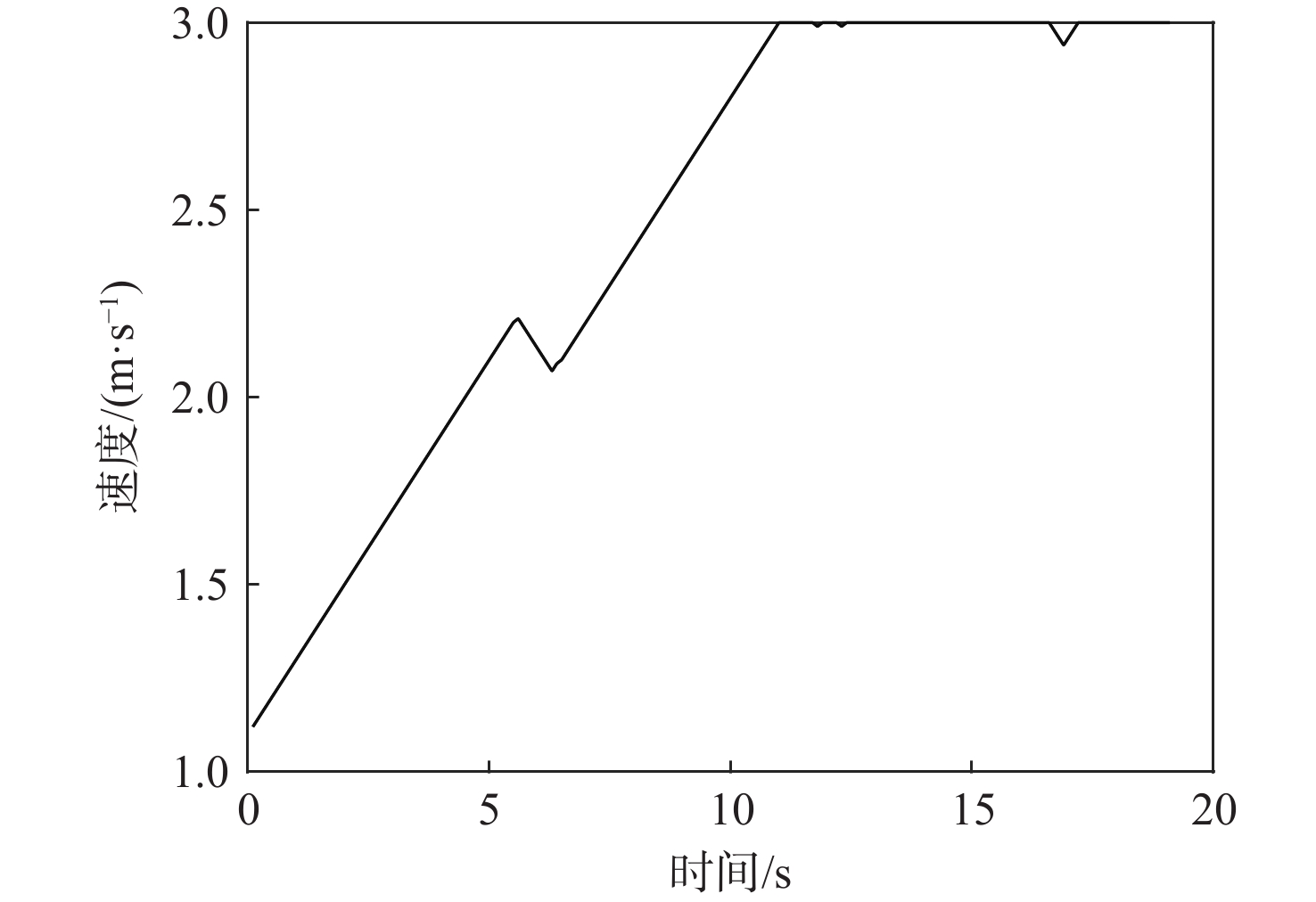
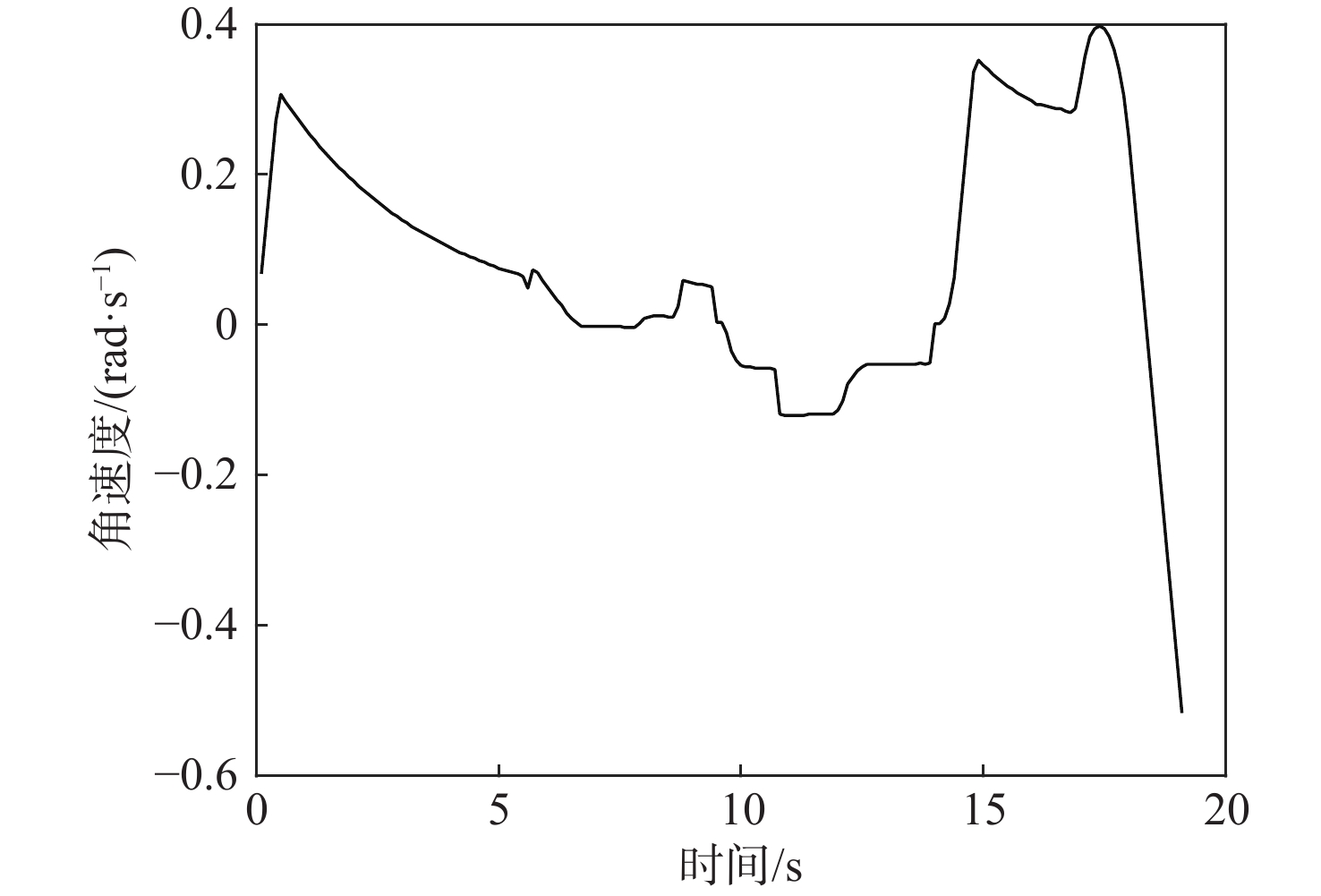
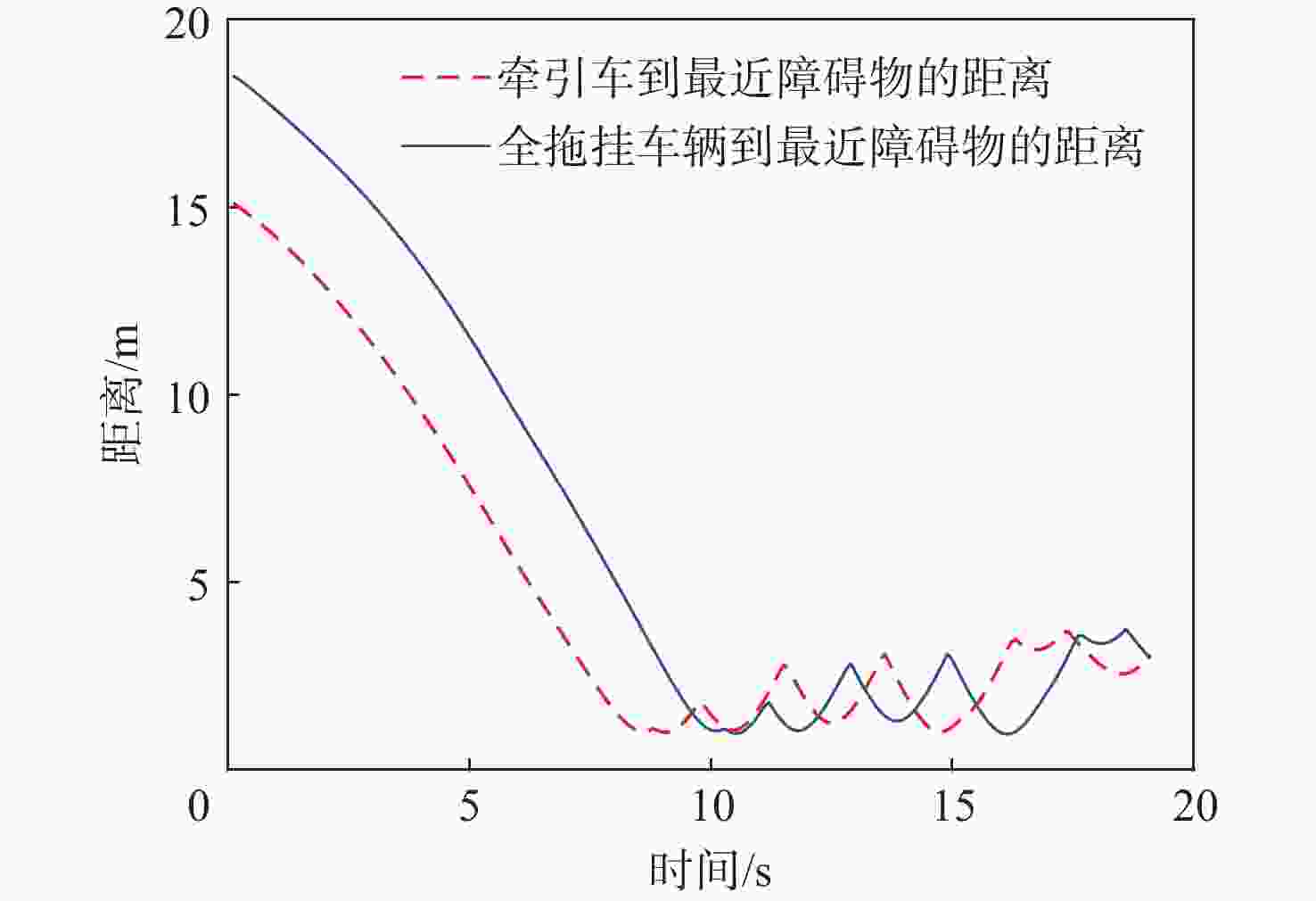
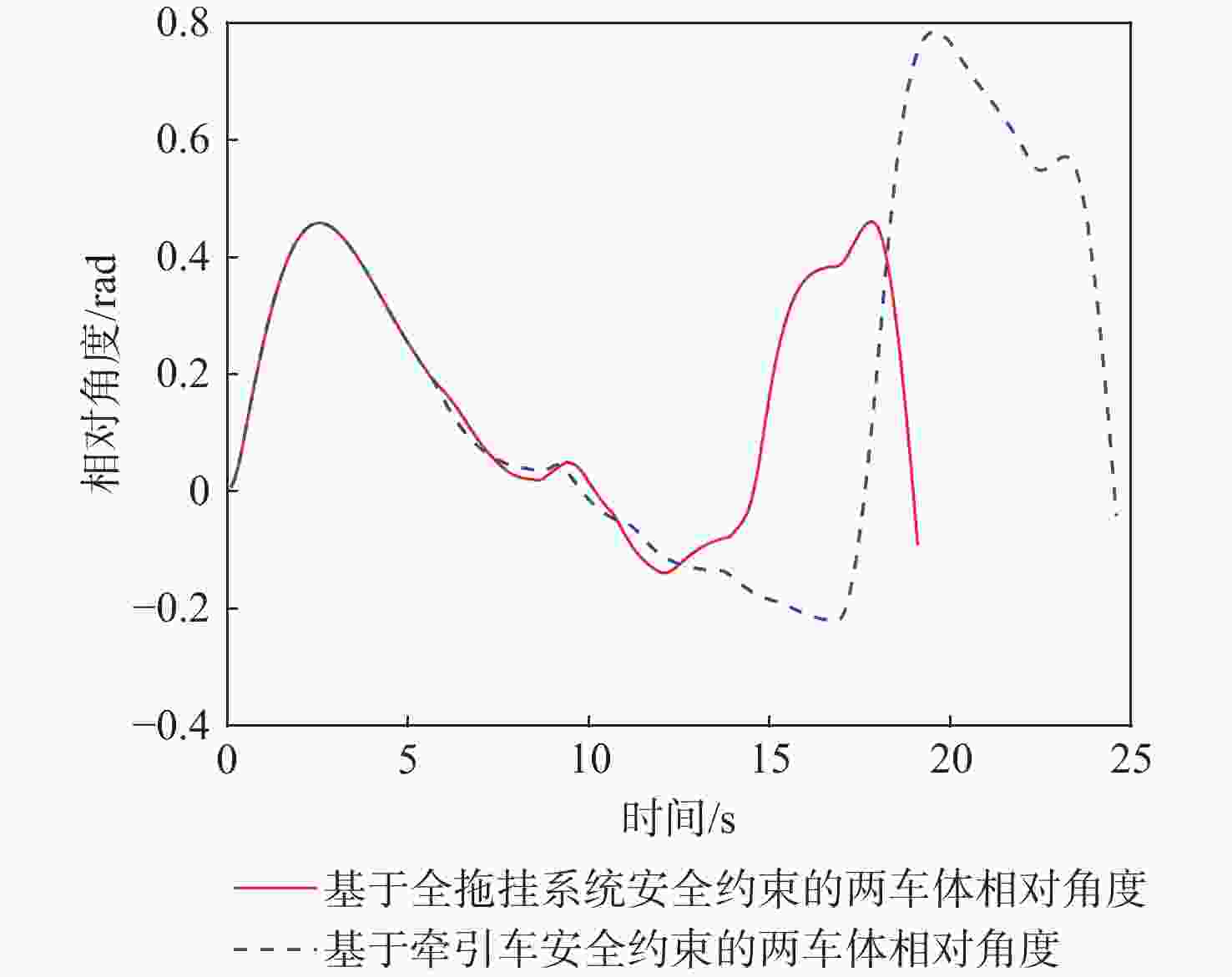
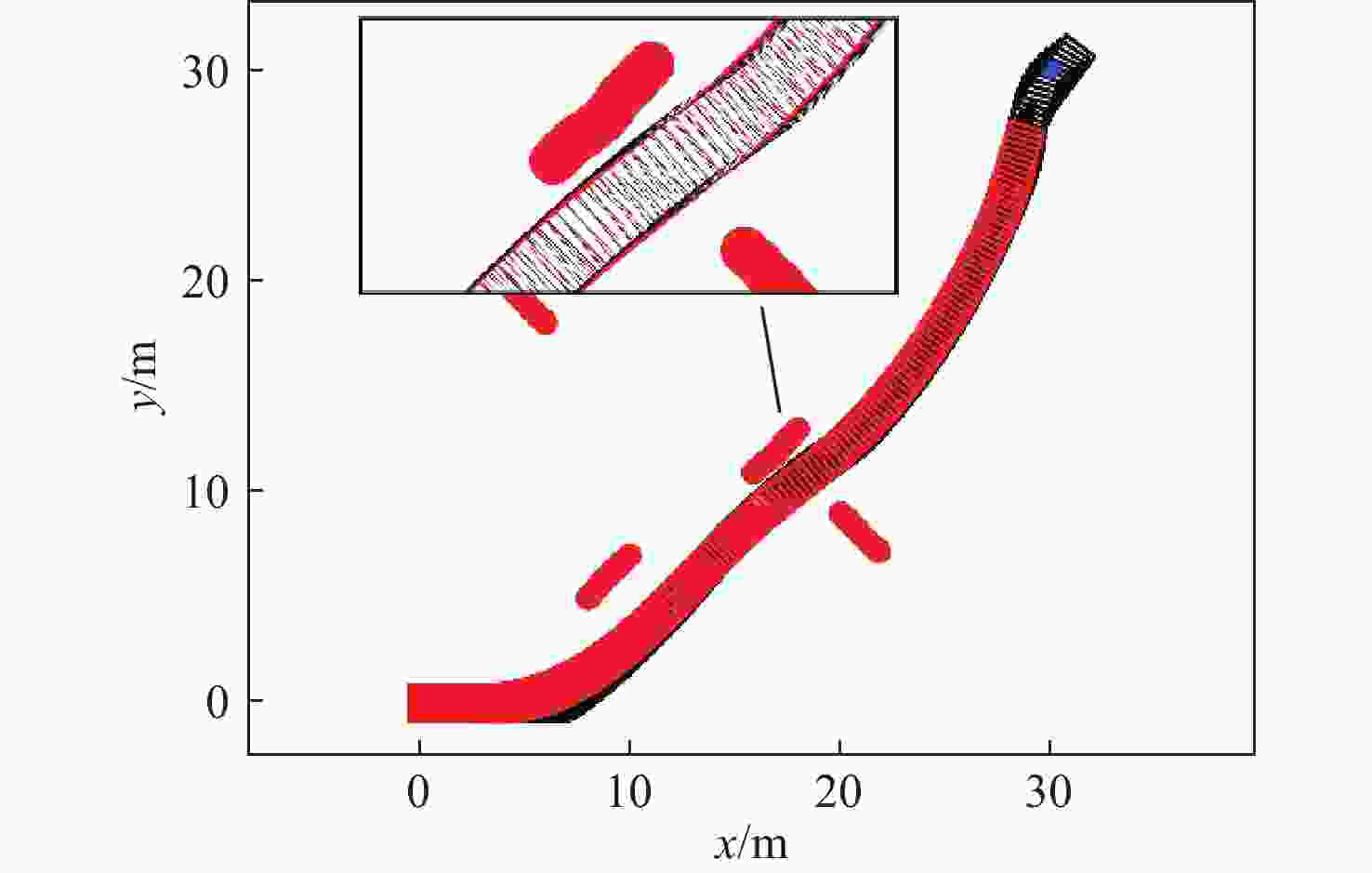
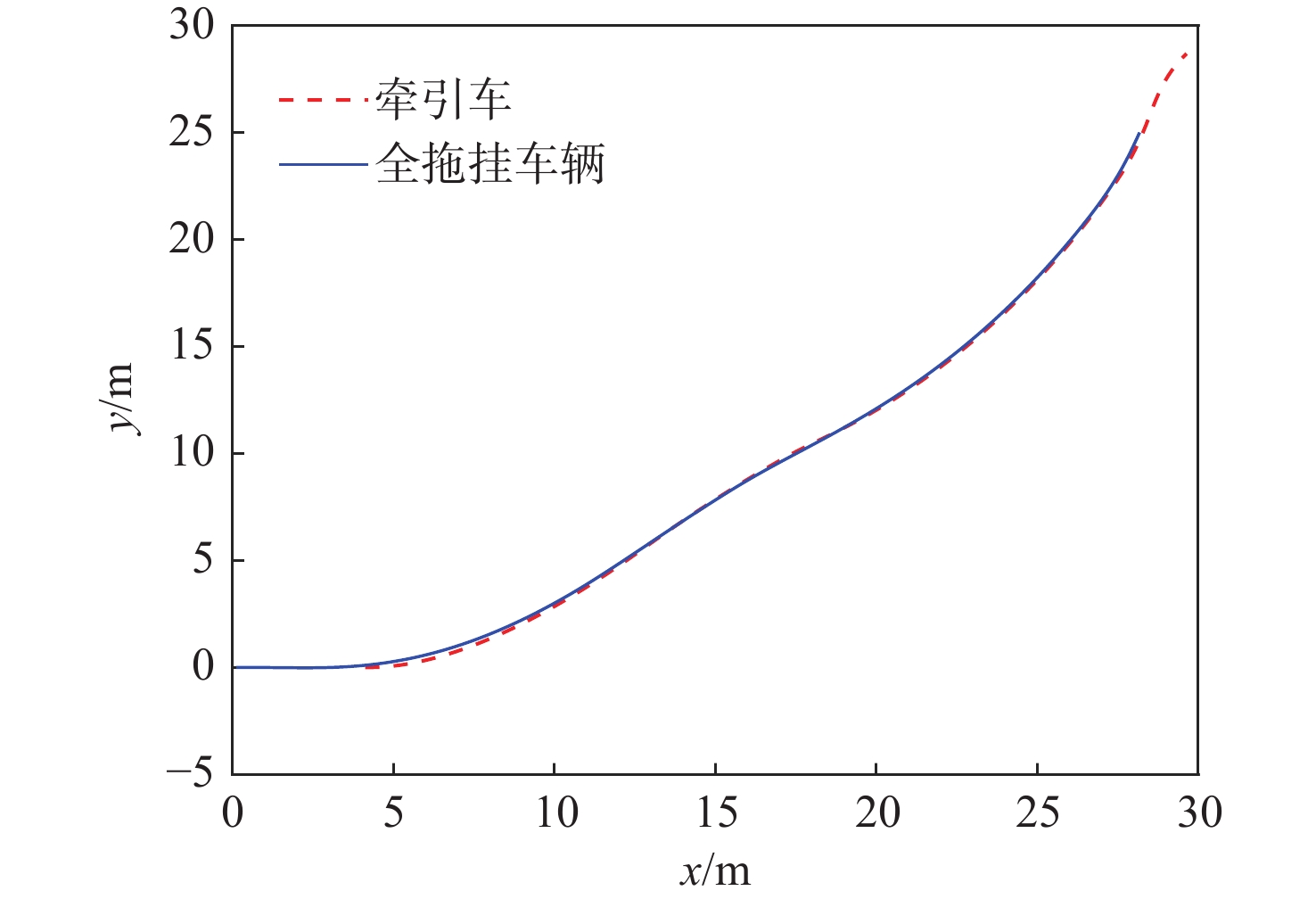
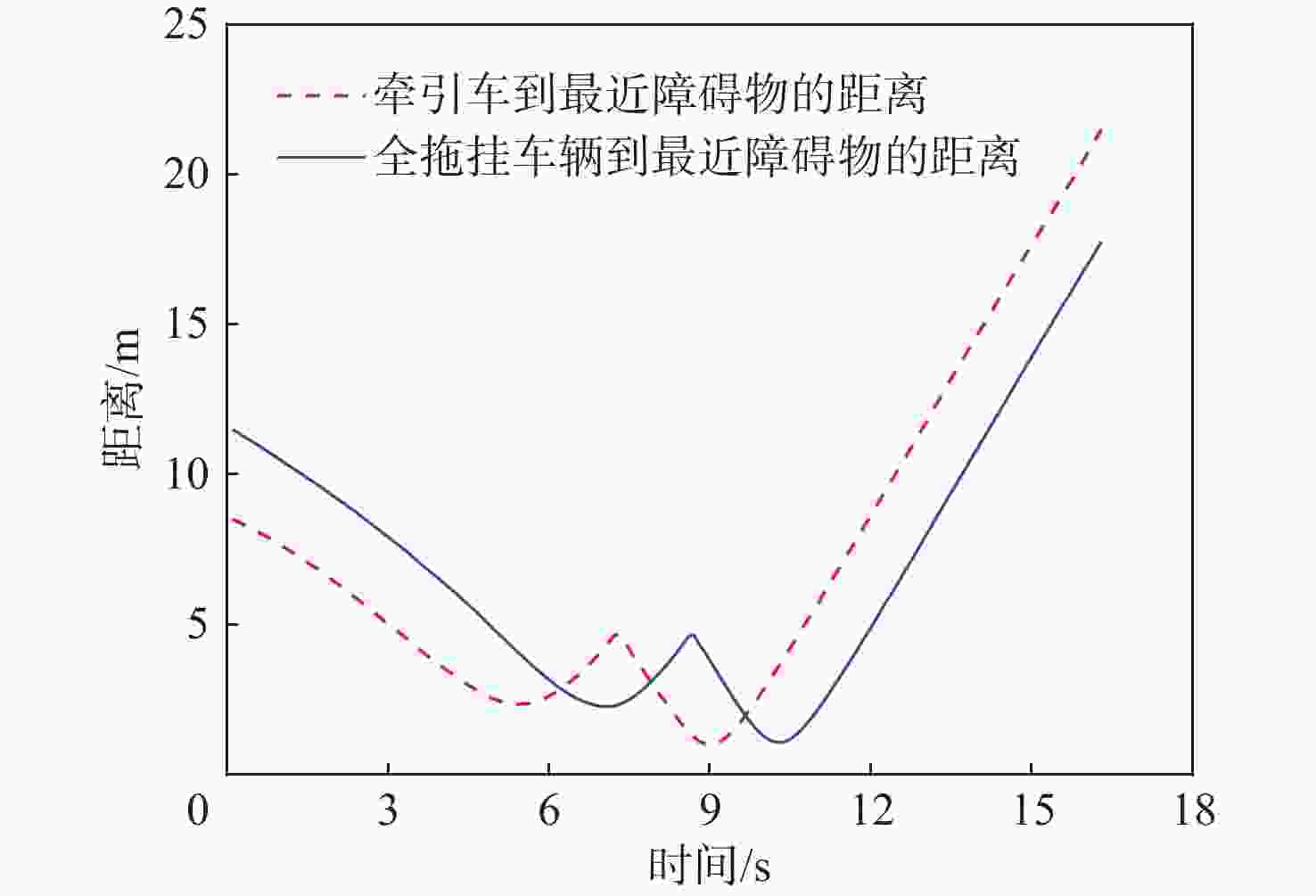
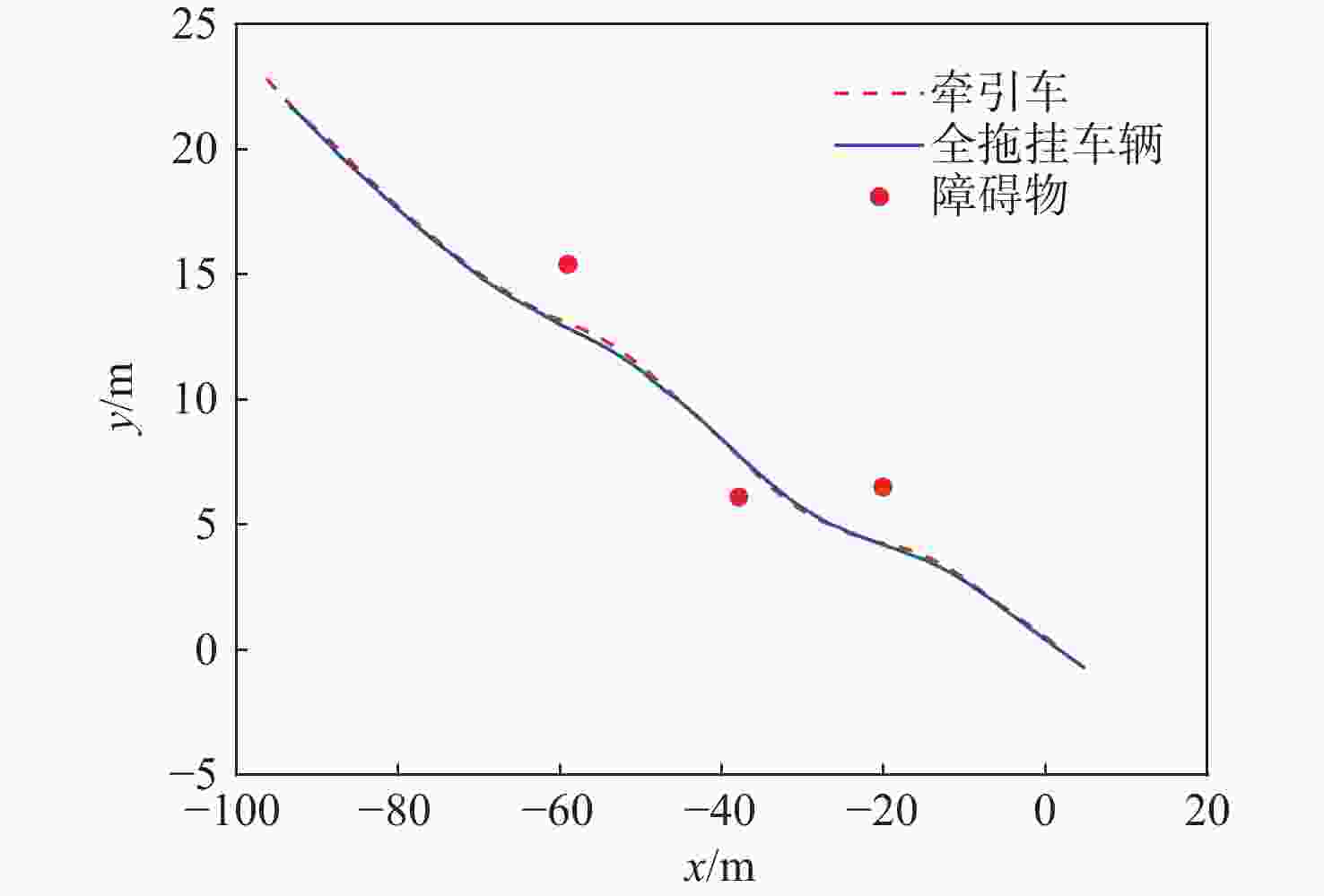
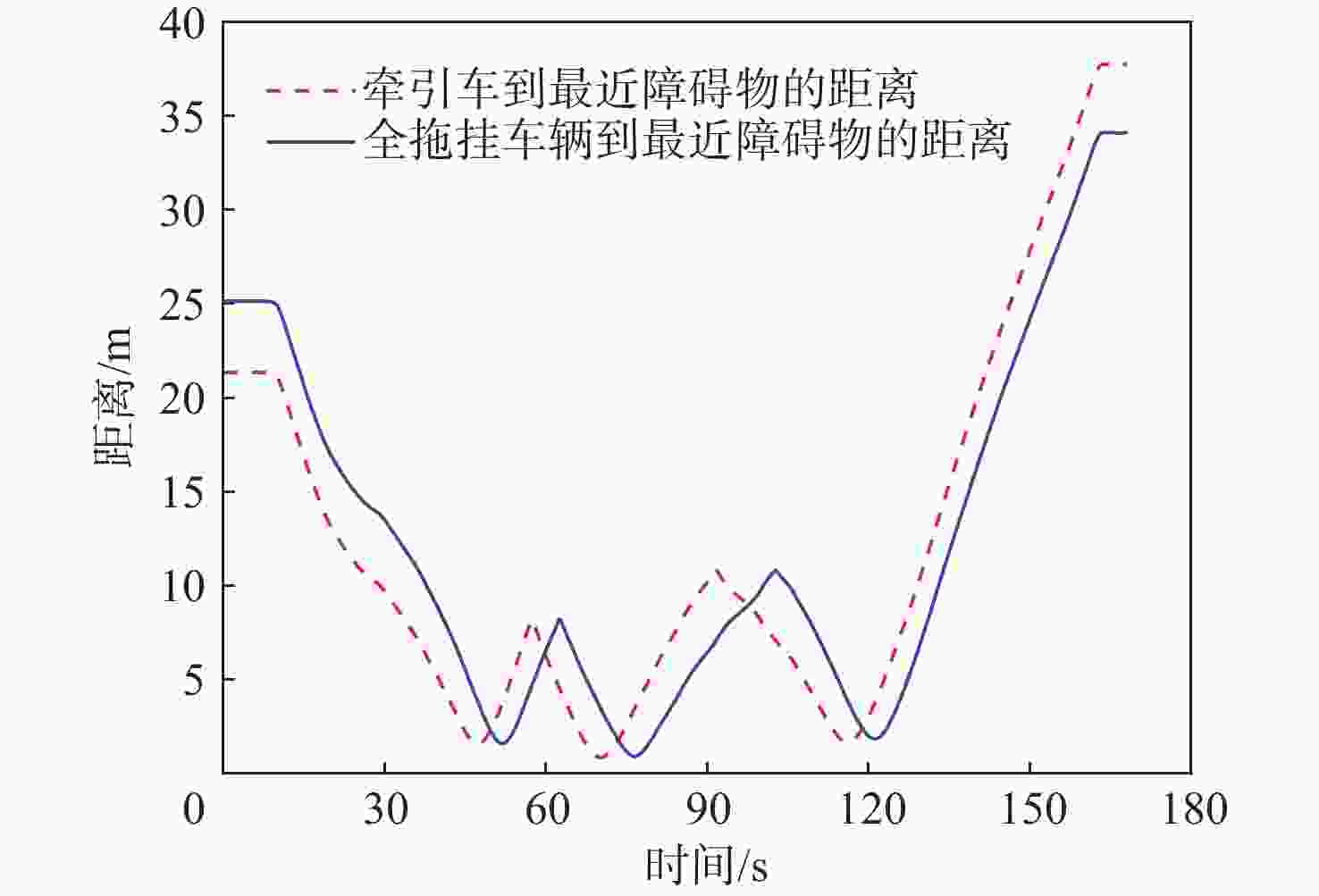
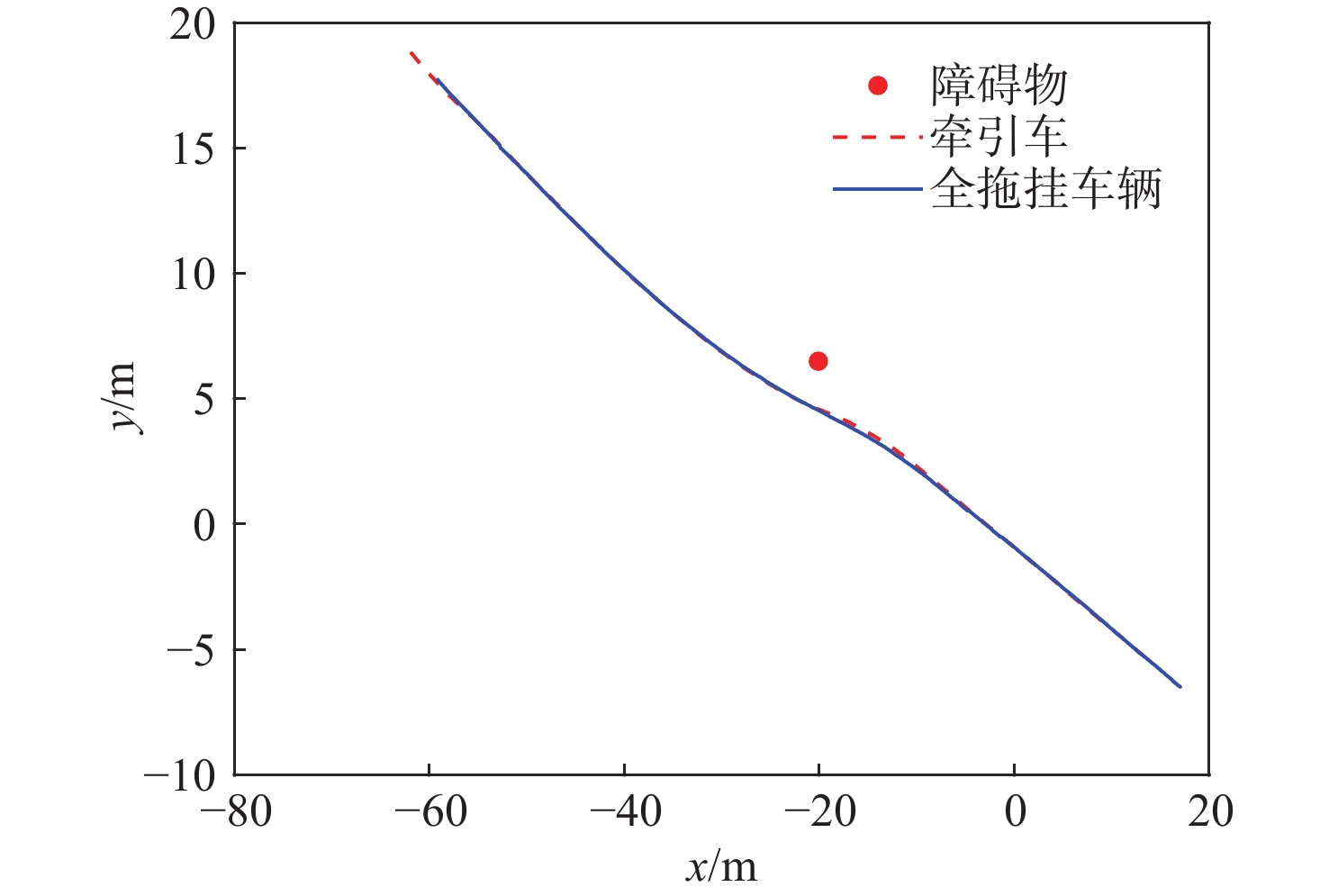
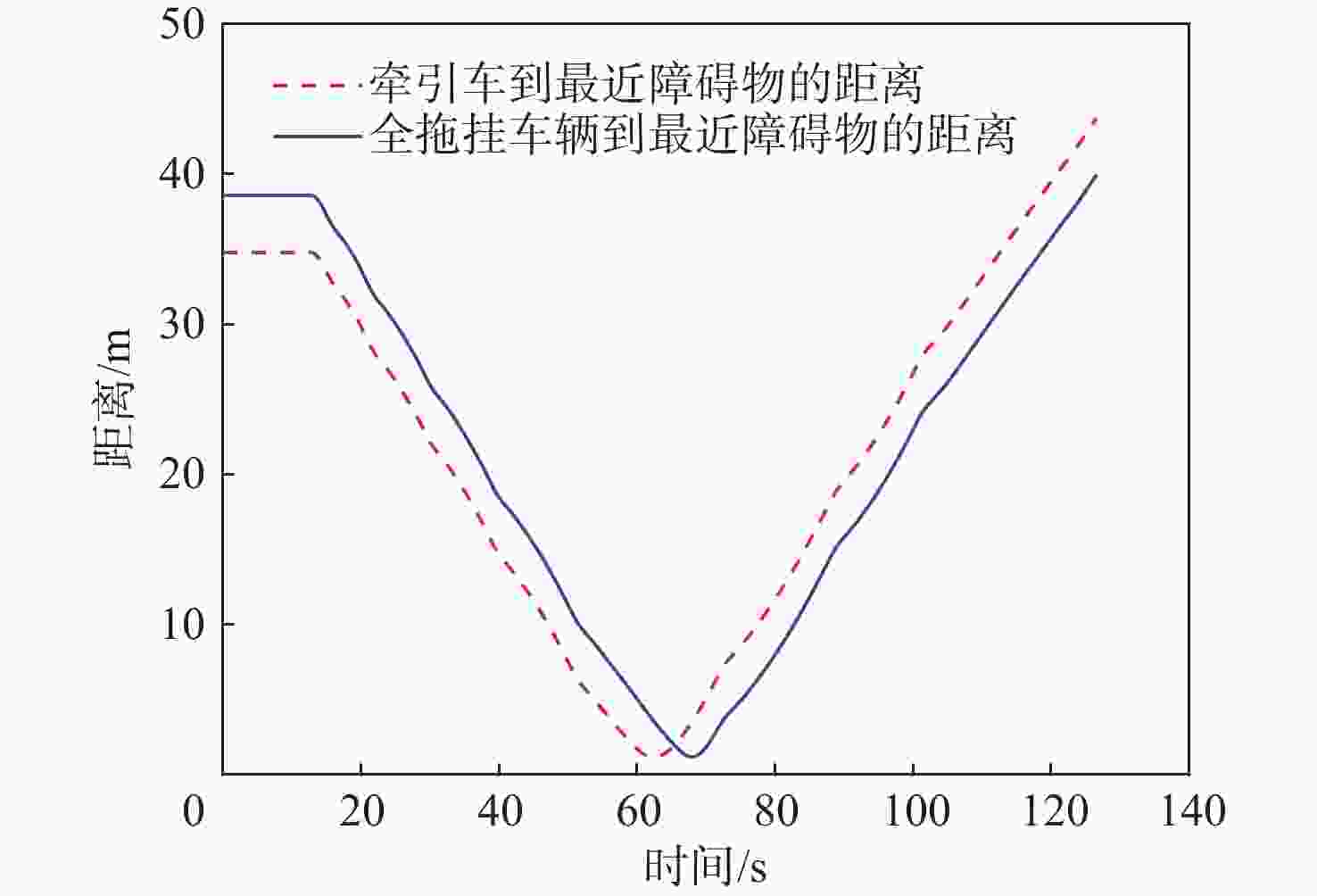
针对普通乘用车的局部规划算法无法充分考虑整个拖挂系统，从而导致全拖挂车辆存在高碰撞风险的问题，提出一种针对离轴式全拖挂系统的改进动态窗口法(DWA)，以实现无人全拖挂系统在非结构化道路下的主动避障。对牵引车速度进行采样，构成速度矢量空间，并根据系统约束和采样值，借助系统运动学模型预测两车体的运动轨迹；引入与目标点位置相关的子评价函数，提出一种符合全拖挂系统的评价函数；根据评价函数选择最优速度，确保系统安全抵达目标点。实验表明：所提方法在避障任务中具有可靠的安全性，在实车实验中，牵引车到障碍物边界的最小距离为0.83 m，全拖挂车辆到障碍物边界的最小距离为0.89 m。
Abstract:Full trailers are at a significant risk of collision since the local planning algorithm for regular passenger cars does not completely account for the entire trailer system. To address this issue, a refined dynamic window approach (DWA) is proposed specifically for off-axis full trailer systems to enable proactive obstacle avoidance for unmanned full trailer systems on unstructured roads. Initially, the sampling of the towing vehicle’s speed constructs a velocity vector space. The motion paths of both vehicles are then forecasted using the kinematic model of the system and the data that were sampled. Subsequently, introducing sub-cost functions related to the target point’s position, an evaluation function tailored to the trailer system is proposed. Finally, the optimal velocity is selected based on the evaluation function to ensure the system safely reaches the target point. Experimental results demonstrate the method’s reliable safety in obstacle avoidance tasks, with a minimum distance of 0.83 meters between the towing vehicle and obstacle boundaries in real vehicle experiments, and 0.89 meters for the full trailer from obstacle boundaries.
-
图 2 离轴式全拖挂车辆转弯半径示意图
Figure 2. Schematic diagram of turning radius for an off-axis full trailer vehicle
图 7 场景1中2种方法避障足迹对比
Figure 7. Comparison of obstacle avoidance footprints of two methods in scenario 1
图 8 场景2中2种方法避障足迹对比
Figure 8. Comparison of obstacle avoidance footprints of two methods in scenario 2
图 10 场景2下基于全拖挂系统的避障速度
Figure 10. Velocity of obstacle avoidance based on full trailer system in scenario 2
图 11 场景2下基于全拖挂系统的避障角速度
Figure 11. Angular velocity of obstacle avoidance based on full trailer system in scenario 2
图 12 场景2下车体到最近障碍物的距离
Figure 12. Distance from vehicle bodies to the nearest obstacle in scenario 2
图 13 场景2下两车体相对角度的对比
Figure 13. Comparison of relative angles of two vehicle bodies in scenario 2
图 14 动态障碍物下基于全拖挂系统的避障足迹
Figure 14. Obstacle avoidance footprint based on full trailer system in case of dynamic obstacles
图 15 动态障碍物下基于全拖挂系统的行驶轨迹
Figure 15. Trajectory based on full trailer system in case of dynamic obstacles
图 16 动态障碍物下基于全拖挂系统的牵引车前轮转角
Figure 16. Steering angle of tractor based on full trailer system in case of dynamic obstacles
图 17 动态障碍物下车体到最近障碍物的距离
Figure 17. Distance from vehicle bodies to the nearest obstacle in case of dynamic obstacles
图 24 单个障碍物下两车体到最近障碍物的距离
Figure 24. Distance from two vehicle bodies to the nearest obstacle under a single obstacle
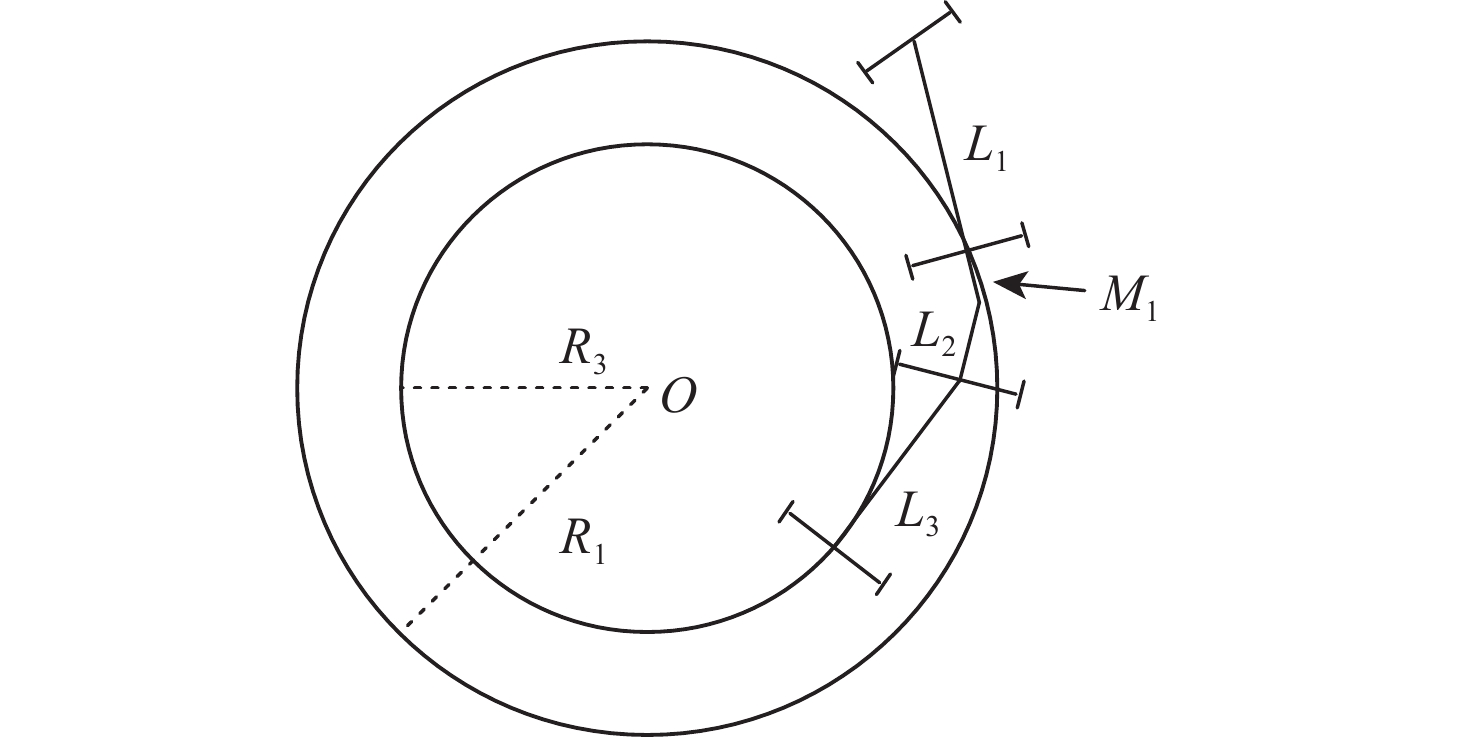
表 1 全拖挂车辆参数
Table 1. Parameters of off-axle full trailer
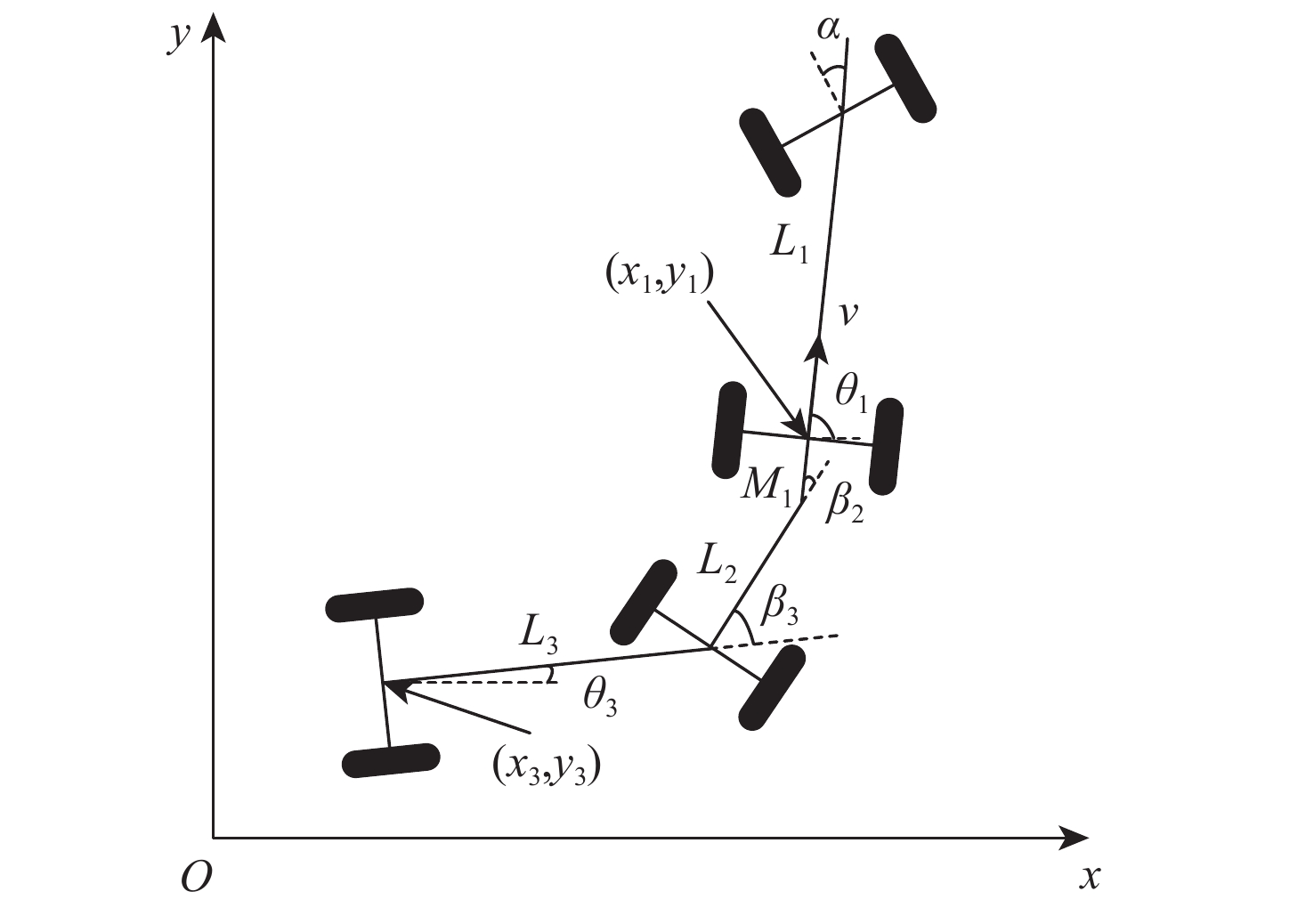
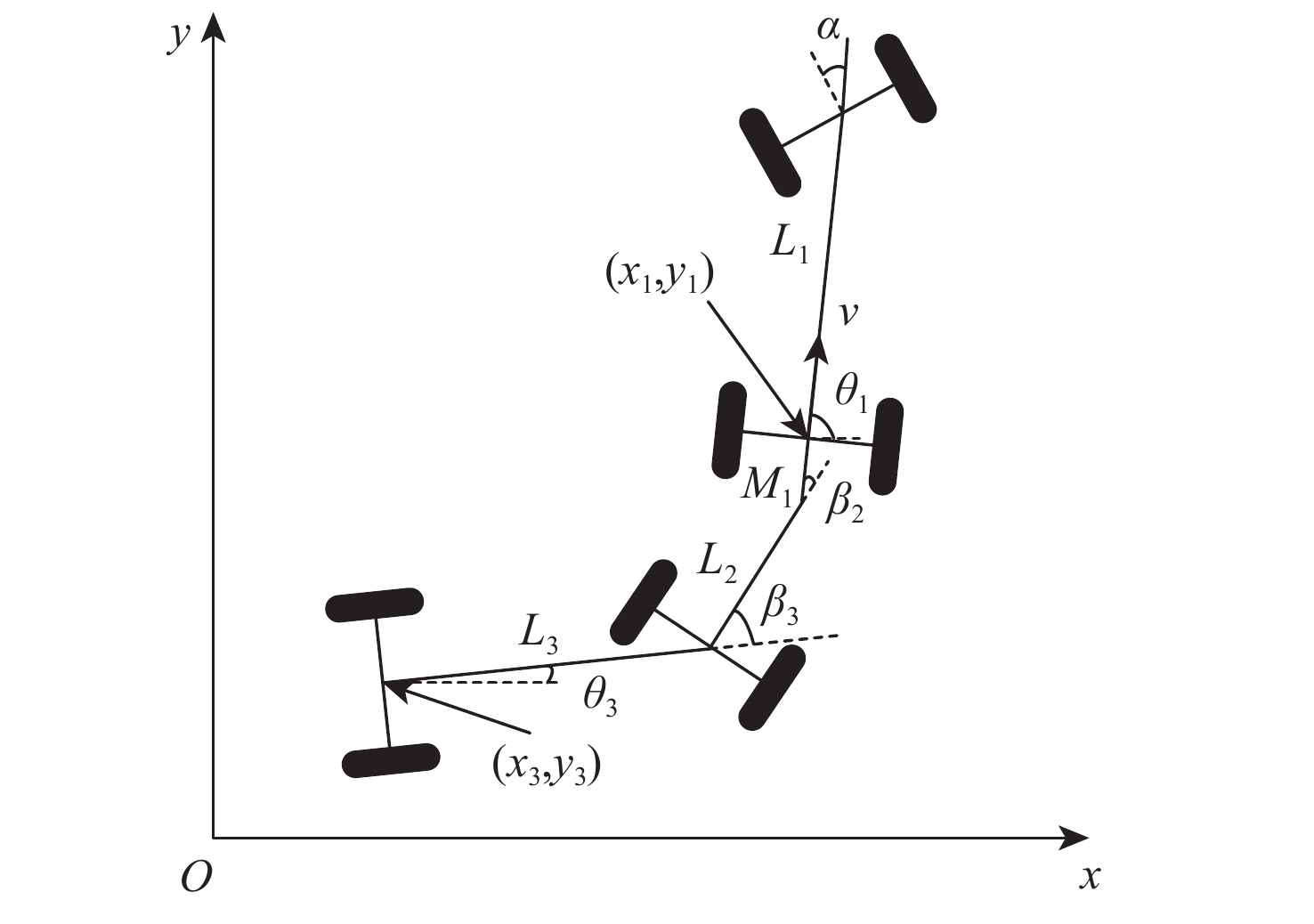
参数 数值 牵引车轴距$ {L_1}/{\mathrm{m}} $ 2.49 全拖挂车辆轴距$ {L_3}/{\mathrm{m}} $ 1.68 牵引车后轴中点到连接点距离$ {M_1}/{\mathrm{m}} $ 0.60 全拖挂车辆前轴中心点到连接点距离$ {L_2}/{\mathrm{m}} $ 1.14 牵引车车宽$ d/{\mathrm{m}} $ 1.66 牵引车车长$ l/{\mathrm{m}} $ 3.36 全拖挂车辆车宽$ {d_{\mathrm{r}}}/{\mathrm{m}} $ 1.66 全拖挂车辆车长$ {l_{\mathrm{r}}}/{\mathrm{m}} $ 2.50 两车体最大相对角度$ {\theta _{{\mathrm{s}}\max }}/{\mathrm{rad}} $ 2.23 
下载: 导出CSV
表 2 避障控制器参数
Table 2. Obstacle Avoidance Controller Parameters
参数 数值 障碍物半径$ R/{\mathrm{m}} $ 0.7/0.8 预测时间$ T/{\mathrm{s}} $ 3.0 牵引车最大速度$ {v_{\max }}/({\text{m}}\cdot{\text{s}}^{-1}) $ 3.0 牵引车最大角速度$ {\omega _{\max }}/({\text{rad}}\cdot{\text{s}}^{-1}) $ 0.7 预测时间间隔$ {{{T}}_{\text{d}}}/{\text{s}} $ 0.1 速度采样分辨率$ {v}_{\text{d}}/(\text{m}\cdot\text{s}^{-1}) $ 0.01 角速度采样分辨率$ {\omega _{\text{d}}}/({\text{rad}}\cdot{\text{s}}^{-1}) $ 0.017 a1、b1、c1、d1 0.15、1.0、1.5、1 a2、b2、c2、d2 0.15、1.0、1.5、1 $ \eta 、\lambda $ 0.3、0.7
下载: 导出CSV
-
[1] JIN C, YONG Z, HOU S M, et al. Stabilization control of a backward tractor-trailer mobile robot[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation. Piscataway: IEEE Press, 2010: 2136-2141. [2] RITZEN P, ROEBROEK E, VAN DE WOUW N, et al. Trailer steering control of a tractor-trailer robot[J]. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1240-1252. doi: 10.1109/TCST.2015.2499699 [3] BERGMAN K, LJUNGQVIST O, AXEHILL D. Improved path planning by tightly combining lattice-based path planning and optimal control[J]. IEEE Transactions on Intelligent Vehicles, 2021, 6(1): 57-66. doi: 10.1109/TIV.2020.2991951 [4] 任玥, 郑玲, 张巍, 等. 基于模型预测控制的智能车辆主动避撞控制研究[J]. 汽车工程, 2019, 41(4): 404-410. doi: 10.19562/j.chinasae.qcgc.2019.04.007REN Y, ZHENG L, ZHANG W, et al. A study on active collision avoidance control of autonomous vehicles based on model predictive control[J]. Automotive Engineering, 2019, 41(4): 404-410(in Chinese). doi: 10.19562/j.chinasae.qcgc.2019.04.007 [5] 牛国臣, 李文帅, 魏洪旭. 基于双五次多项式的智能汽车换道轨迹规划[J]. 汽车工程, 2021, 43(7): 978-986. doi: 10.19562/j.chinasae.qcgc.2021.07.004NIU G C, LI W S, WEI H X. Intelligent vehicle lane changing trajectory planning based on double quintic polynomials[J]. Automotive Engineering, 2021, 43(7): 978-986(in Chinese). doi: 10.19562/j.chinasae.qcgc.2021.07.004 [6] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Piscataway: IEEE Press, 1985: 500-505. [7] LIM W, LEE S, SUNWOO M, et al. Hierarchical trajectory planning of an autonomous car based on the integration of a sampling and an optimization method[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(2): 613-626. doi: 10.1109/TITS.2017.2756099 [8] YI B L, BENDER P, BONARENS F, et al. Model predictive trajectory planning for automated driving[J]. IEEE Transactions on Intelligent Vehicles, 2019, 4(1): 24-38. doi: 10.1109/TIV.2018.2886683 [9] ZENG J, ZHANG B K, SREENATH K. Safety-critical model predictive control with discrete-time control barrier function[C]//Proceedings of the American Control Conference. Piscataway: IEEE Press, 2021: 3882-3889. [10] FOX D, BURGARD W, THRUN S. The dynamic window approach to collision avoidance[J]. IEEE Robotics & Automation Magazine, 1997, 4(1): 23-33. [11] BAI G X, LIANG C, MENG Y, et al. Obstacle avoidance of semi-trailers based on nonlinear model predictive control[J]. World Electric Vehicle Journal, 2019, 10(4): 72. doi: 10.3390/wevj10040072 [12] BERLIN J, HESS G, KARLSSON A, et al. Trajectory generation for mobile robots in a dynamic environment using nonlinear model predictive control[C]//Proceedings of the IEEE 17th International Conference on Automation Science and Engineering. Piscataway: IEEE Press, 2021: 942-947. [13] ASROFUDIN B, WIDYOTRIATMO A, SIREGAR P I, et al. Sigmoid function optimization for path following control with obstacle avoidance of an autonomous truck-trailer[C]//Proceedings of the International Conference on Instrumentation, Control, and Automation. Piscataway: IEEE Press, 2021: 180-185. [14] LJUNGQVIST O, EVESTEDT N, CIRILLO M, et al. Lattice-based motion planning for a general 2-trailer system[C]//Proceedings of the IEEE Intelligent Vehicles Symposium. Piscataway: IEEE Press, 2017: 819-824. [15] CHENG J, ZHANG Y, WANG Z H. Motion planning algorithm for tractor-trailer mobile robot in unknown environment[C]//Proceedings of the 8th International Conference on Natural Computation. Piscataway: IEEE Press, 2012: 1050-1055. [16] LAVALLE S M. Rapidly-exploring random trees: progress and prospects[C]//Proceedings of the 4th International workshop on the Algorithmic Foundations of Robotics. Wellesley: [s.n.], 2001: 293-308. [17] 白国星, 刘立, 孟宇, 等. 基于非线性模型预测控制的农用拖挂车避障控制器研究[J]. 农业机械学报, 2019, 50(4): 356-362.BAI G X, LIU L, MENG Y, et al. Study of obstacle avoidance controller of agricultural tractor-trailers based on predictive control of nonlinear model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(4): 356-362(in Chinese). [18] SUN F C, HUANG Y L, YUAN J, et al. A compound PRM method for path planning of the tractor-trailer mobile robot[C]//Proceedings of the IEEE International Conference on Automation and Logistics. Piscataway: IEEE Press, 2007: 1880-1885. [19] KAVRAKI L E, SVESTKA P, LATOMBE J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J]. IEEE Transactions on Robotics and Automation, 1996, 12(4): 566-580. doi: 10.1109/70.508439 [20] LJUNGQVIST O, EVESTEDT N, AXEHILL D, et al. A path planning and path-following control framework for a general 2-trailer with a car-like tractor[J]. Journal of Field Robotics, 2019, 36(8): 1345-1377. doi: 10.1002/rob.21908 [21] 杨凯, 黄亚楼, 徐国华. 带拖车的轮式移动机器人系统的建模与仿真[J]. 系统仿真学报, 2000, 12(1): 43-46. doi: 10.16182/j.cnki.joss.2000.01.012YANG K, HUANG Y L, XU G H. Modeling and simulation of tractor trailor robot systems’ kinematics[J]. Acta Simulata Systematica Sinica, 2000, 12(1): 43-46(in Chinese). doi: 10.16182/j.cnki.joss.2000.01.012 [22] 苑晶, 黄亚楼, 孙凤池. 两种连接形式的拖挂式移动机器人路径跟踪控制[J]. 控制理论与应用, 2008, 25(3): 398-406.YUAN J, HUANG Y L, SUN F C. Path following control for tractor-trailer mobile robots with two kinds of connection forms[J]. Control Theory & Applications, 2008, 25(3): 398-406(in Chinese). [23] CHEN L K, SHIEH Y A. Jackknife prevention for articulated vehicles using model reference adaptive control[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2011, 225(1): 28-42. doi: 10.1243/09544070JAUTO1513 -
下载:
点击查看大图
计量
- 文章访问数: 111
- HTML全文浏览量: 33
- PDF下载量: 6
- 被引次数: 0
