Optimization of aircraft speed vector control based on Hp adaptive pseudo-spectral method
-
摘要:
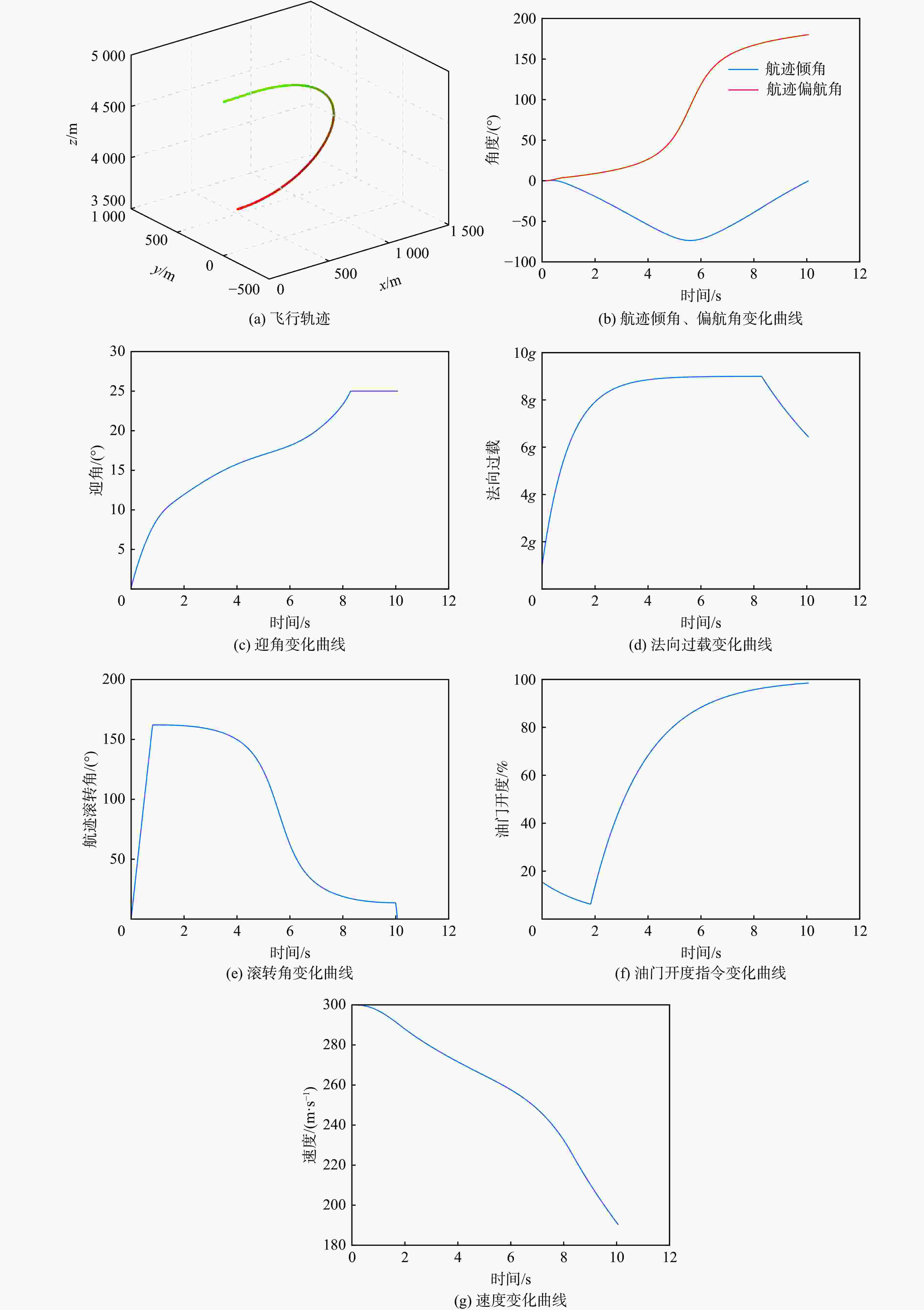
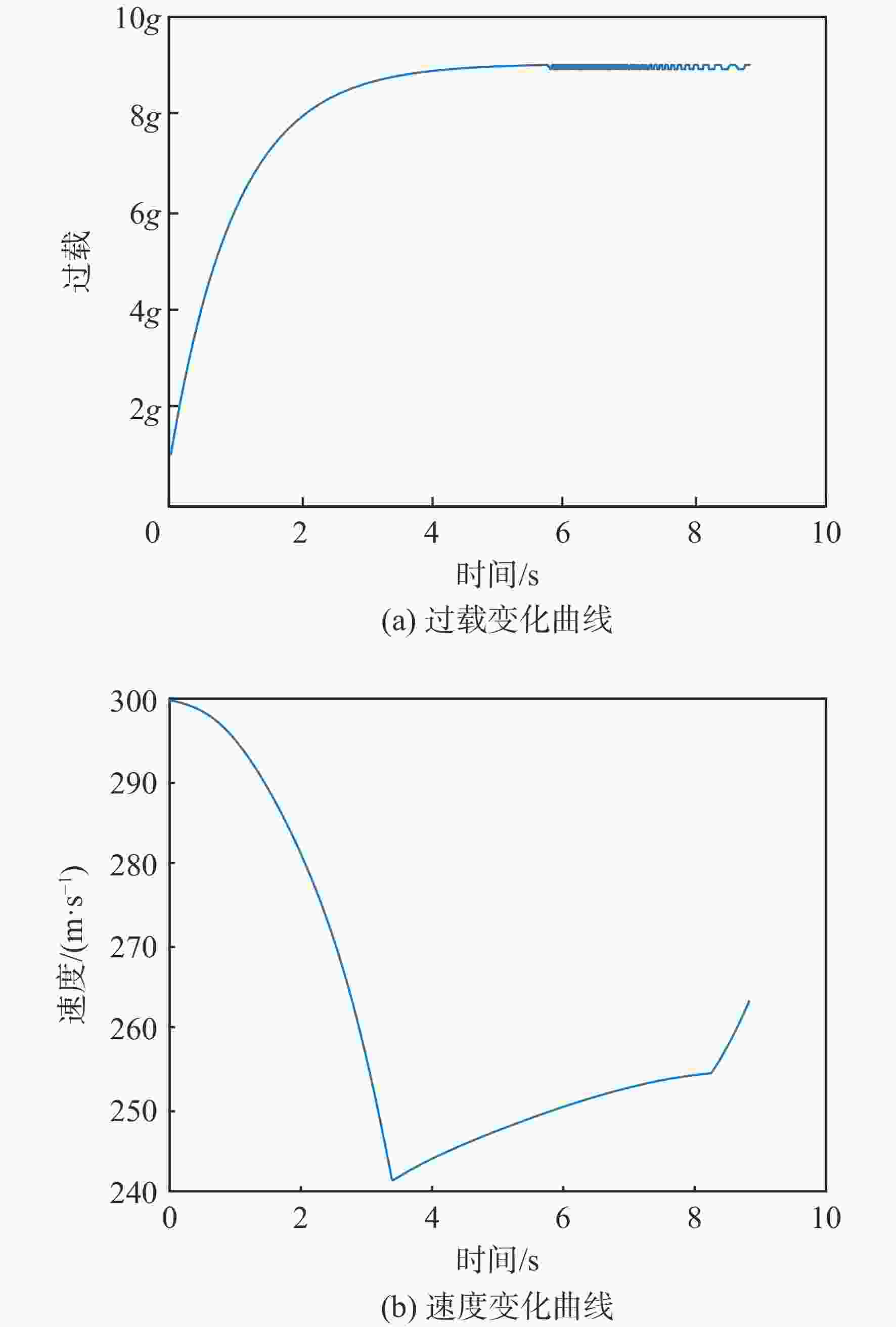
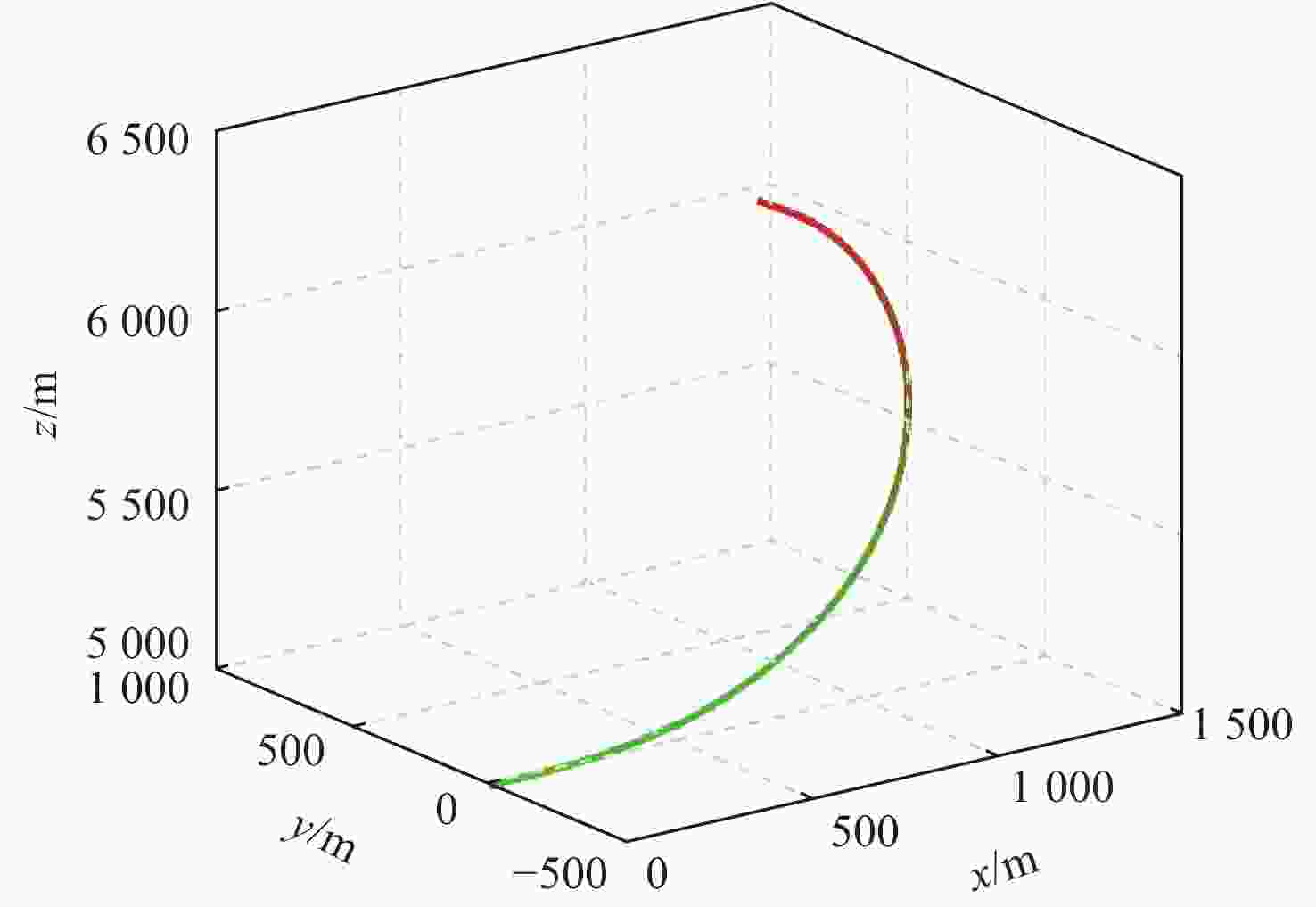
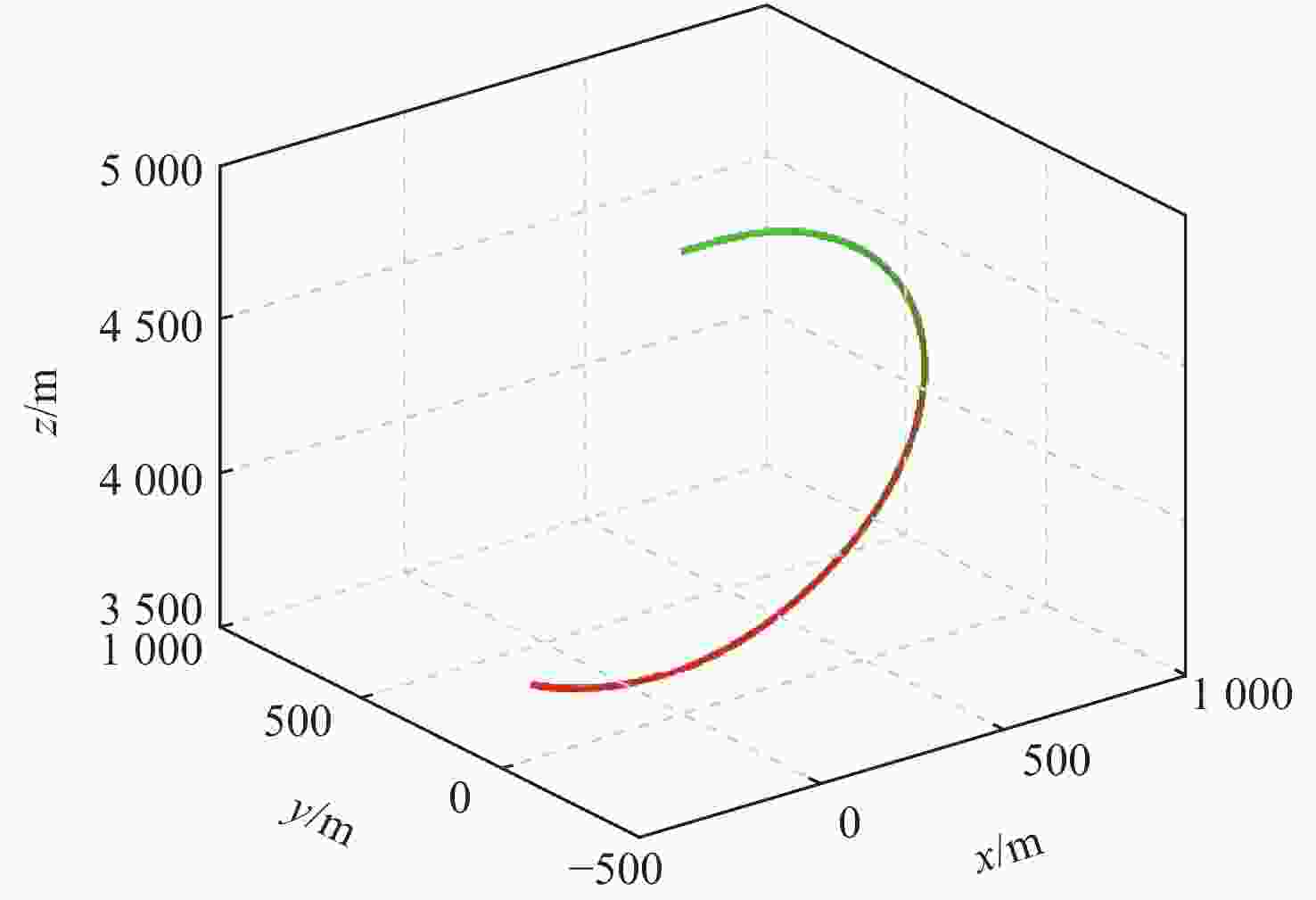
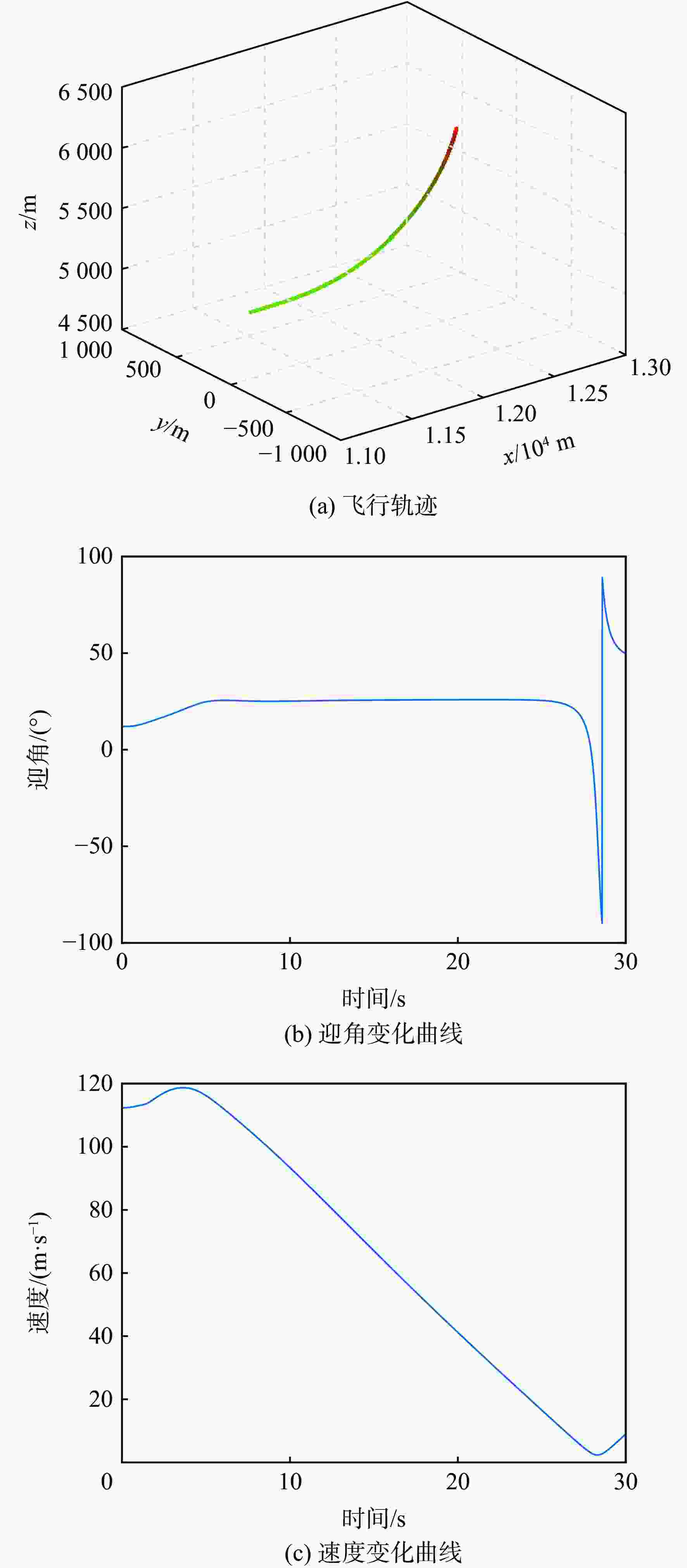
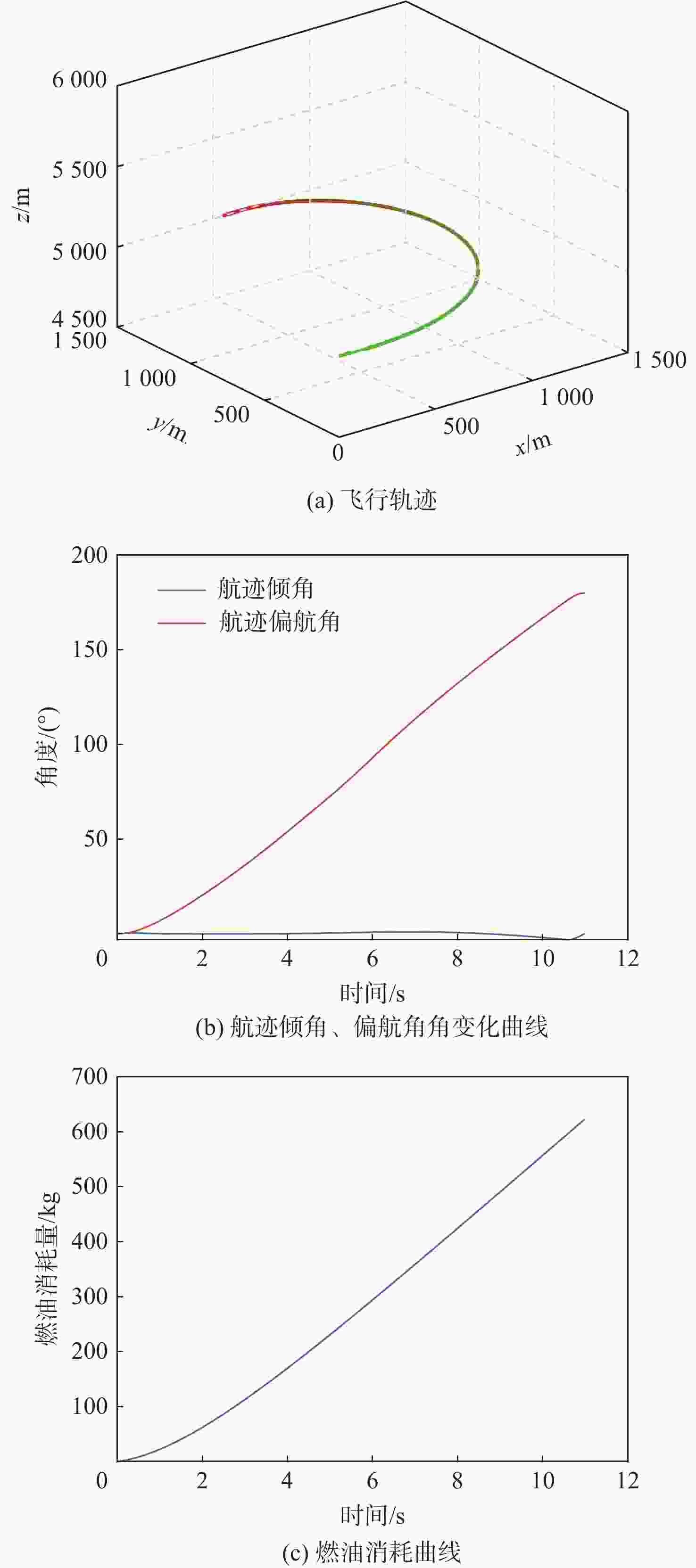
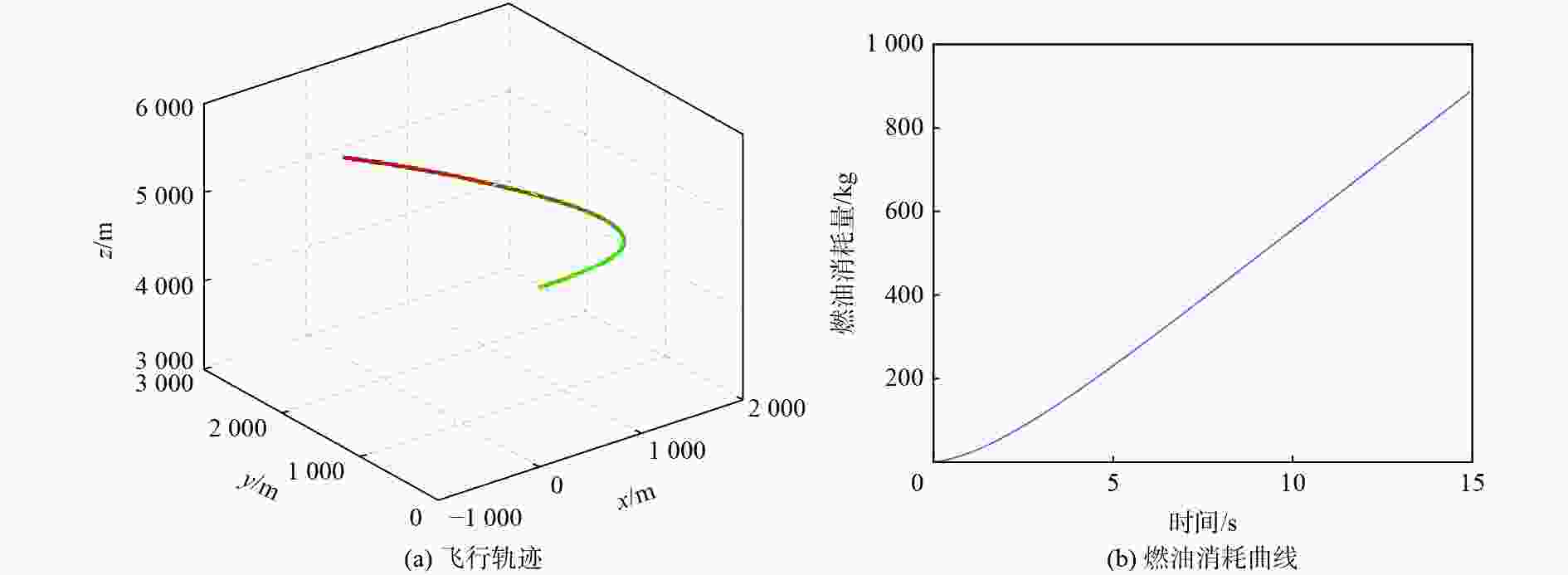
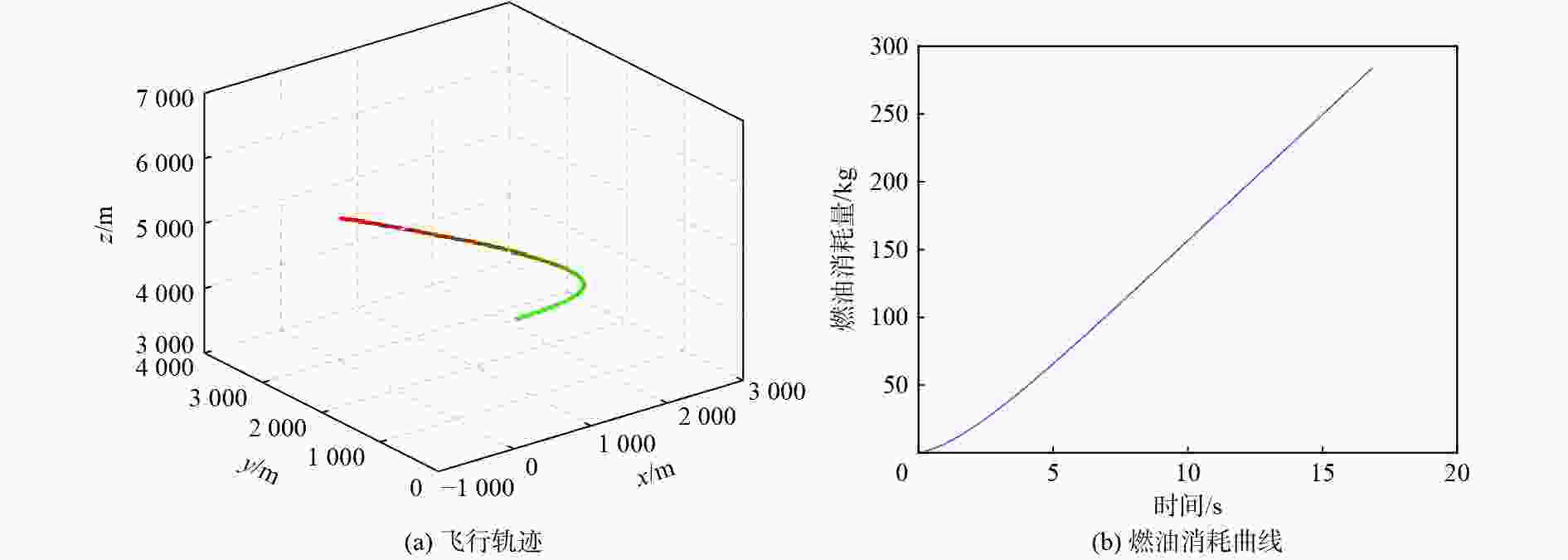
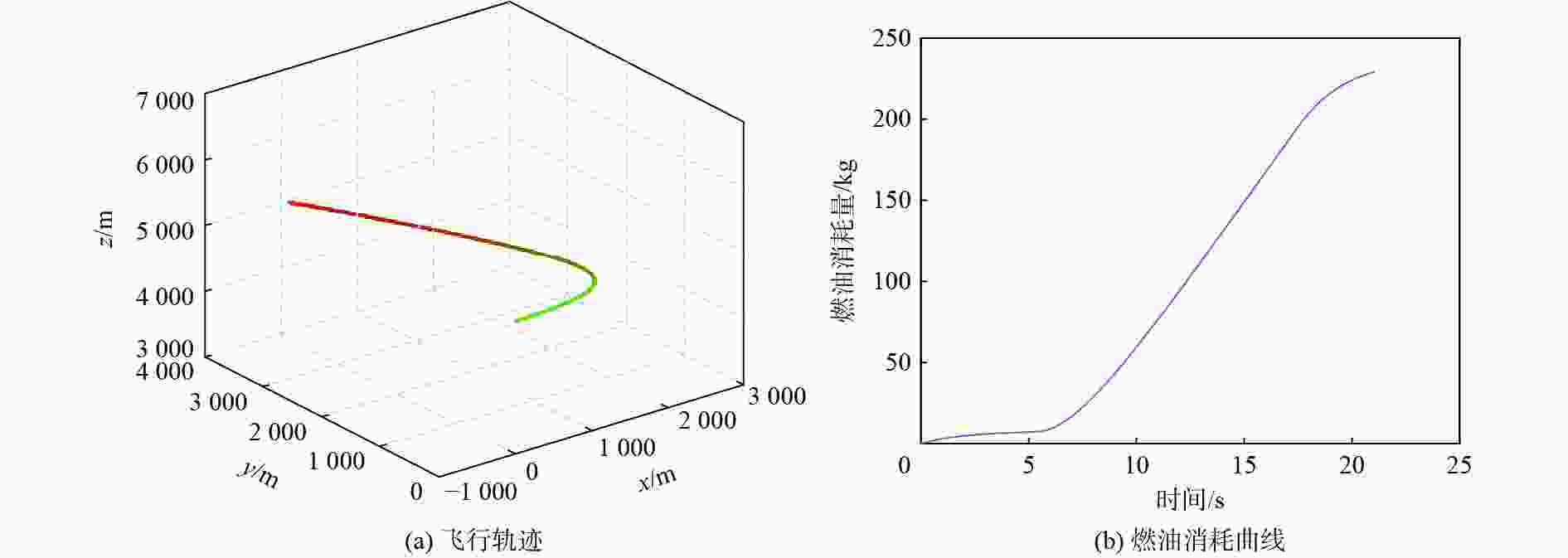
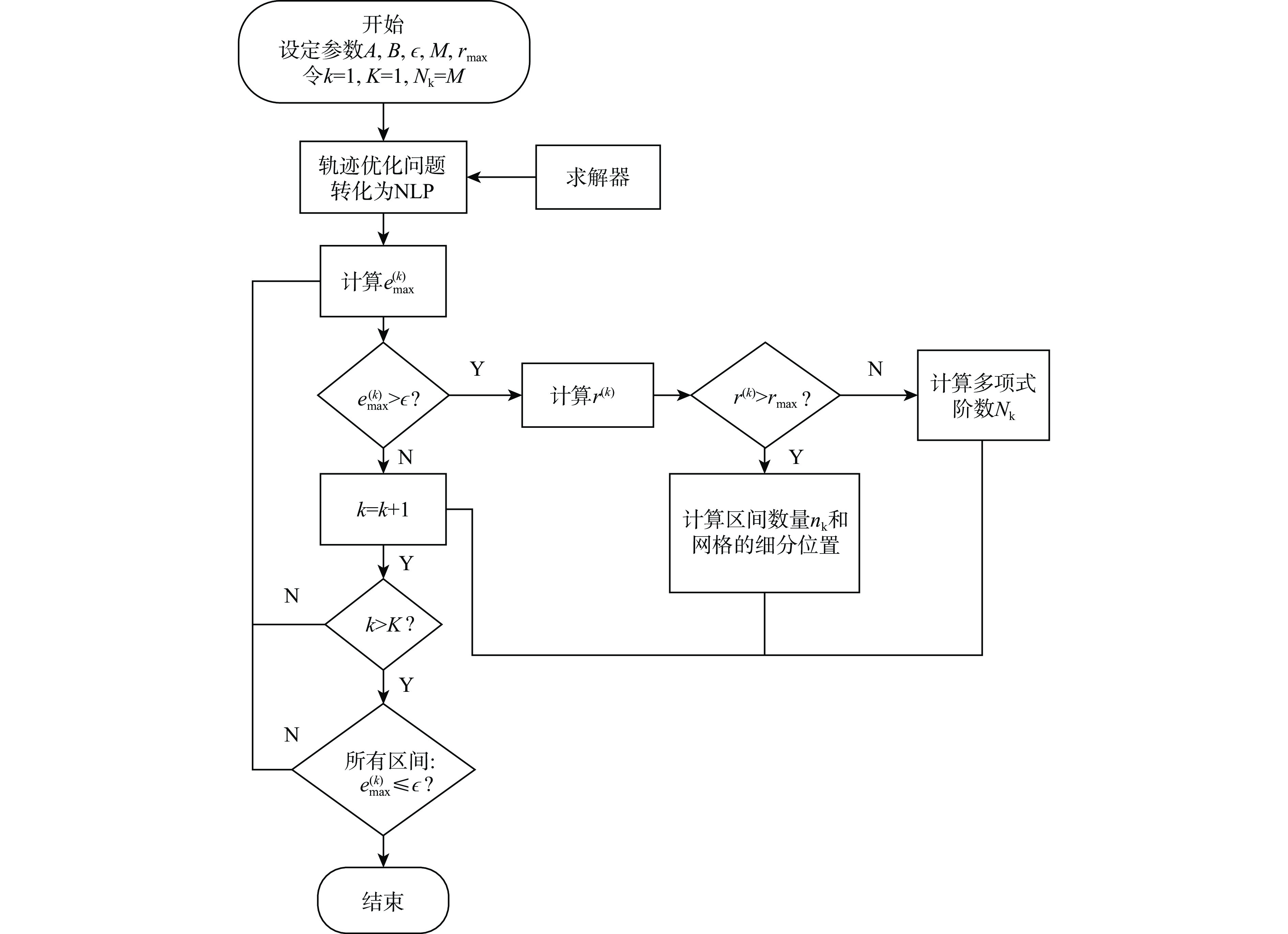
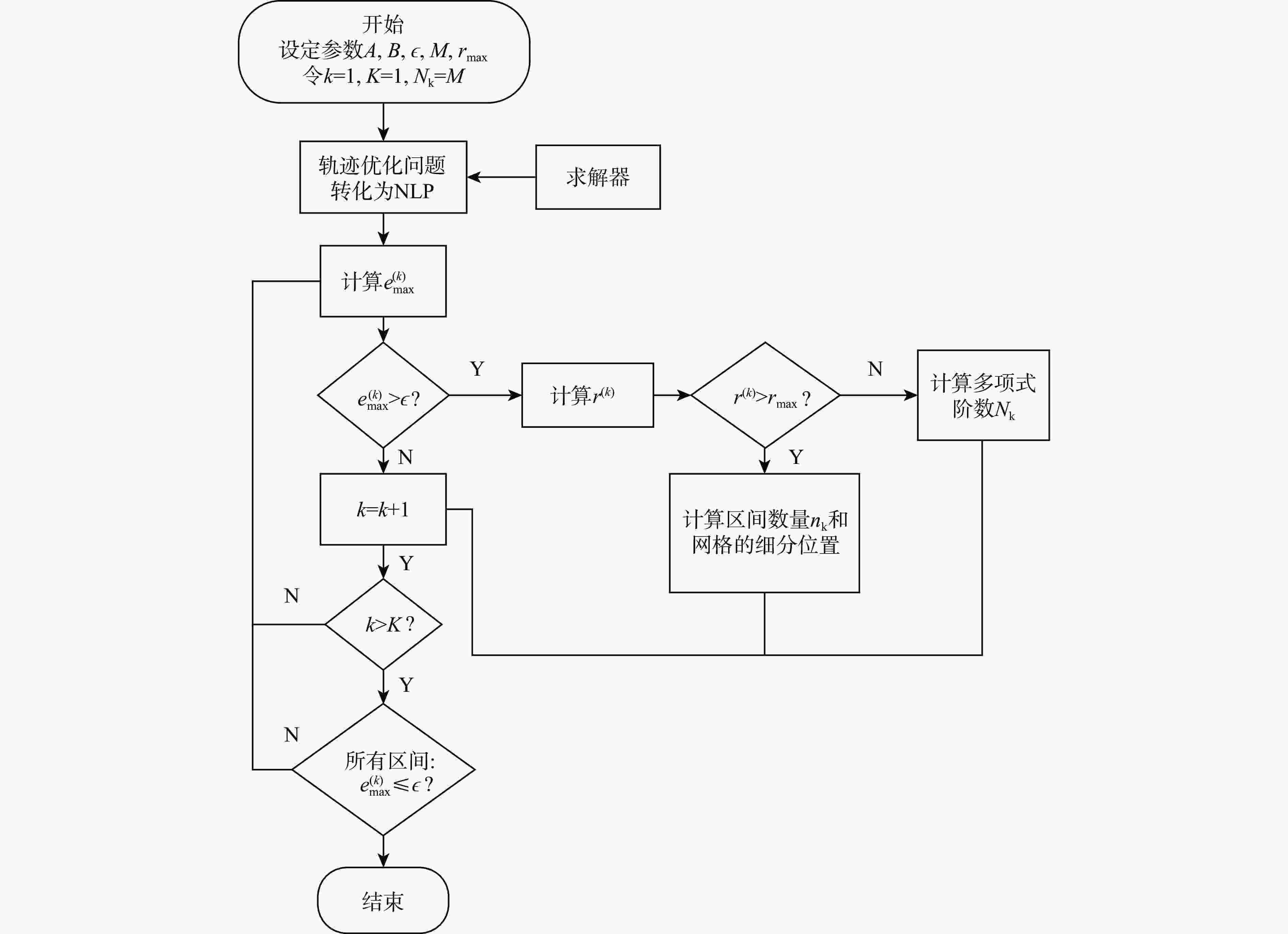
采用Hp自适应伪谱法对速度矢量控制问题进行优化求解。建立基于航迹坐标系的非线性飞机动力学模型，建模时将飞机的过载、推力及滚转的动态响应以动态环节形式进行描述，并通过路径约束实现了实际飞行控制律中的迎角限制功能。通过对控制量、状态量及目标函数的设定实现不同的战术需求，进而利用伪谱法进行优化求解。仿真结果验证了基于Hp自适应伪谱法的速度矢量控制优化的有效性，并展示了在特定场景中处理各种约束的可行性。
Abstract:The Hp adaptive pseudo-spectral method is used to optimize and solve the velocity vector control problem. The track coordinate system is used to create a nonlinear aircraft dynamics model. During the modeling, the dynamic responses of the aircraft’s overload, thrust and roll are described in the form of dynamic links, and the angle of attack limitation function in the actual flight control law is realized through path constraints. Different tactical requirements are achieved by setting the control quantity, state quantity, and objective function, and then the pseudo-spectral method is used for optimization and solution. Based on the Hp adaptive pseudo-spectral method, the simulation results show that the velocity vector control optimization method is effective and that it is feasible to handle different restrictions in certain situations.
-
图 4 30°目标航迹倾角最快转向飞机状态曲线
Figure 4. Fastest turning aircraft status curve at 30° target track inclination angle
图 6 路径最短速度矢量控制法飞机状态曲线
Figure 6. Aircraft state curve with shortest path speed vector control method
图 7 高度约束最快转向飞机状态曲线
Figure 7. Altitude-constrained fastest turning aircraft state curve
-
[1] GHASEMI R, NIKRAVESH S, MENHAJ M, et al. A near optimal fuzzy modeling of pursuit-evasion in an air combat[J]. WSEAS Transactions on Mathematics, 2004, 3(3): 514-521. [2] 张翔伦, 杨蔷薇. 基于机动动作库的实时轨迹生成与仿真研究[J]. 飞行力学, 2008, 26(3): 29-32.ZHANG X L, YANG Q W. Research on real-time trajectory generation based on tactical maneuvers data base[J]. Journal of Flight Dynamics, 2008, 26(3): 29-32(in Chinese). [3] 禹春梅. 飞行器在线轨迹规划与制导控制方法研究[D]. 长沙: 国防科技大学, 2018.YU C M. Research on online trajectory planning and guidance control for aircraft[D]. Changsha: National University of Defense Technology, 2018(in Chinese). [4] 郭铁丁. 深空探测小推力轨迹优化的间接法与伪谱法研究[D]. 北京: 清华大学, 2012.GUO T D. Study of indirect and pseudospectral methods for low thrust trajectory optimization in deep space exploration[D]. Beijing: Tsinghua University, 2012(in Chinese). [5] 崔凯凯, 韩维, 刘玉杰, 等. 基于DM-DSC的舰载机着舰自动复飞控制算法[J]. 北京航空航天大学学报, 2023, 49(4): 900-912.CUI K K, HAN W, LIU Y J, et al. Automatic wave-off control algorithm for carrier aircraft based on DM-DSC[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(4): 900-912(in Chinese). [6] 郑金库, 唐胜景, 郭杰. 高超声速滑翔飞行器预测校正闭环协同末制导方法[J]. 北京航空航天大学学报, 2023, 49(11): 3188-3196.ZHENG J K, TANG S J, GUO J. Closed-loop cooperative terminal guidance law based on predictor-corrector for hypersonic gliding vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(11): 3188-3196(in Chinese). [7] 雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙: 国防科学技术大学, 2008.YONG E M. Study on trjector optimization and guidance approach for hypersonic glide-reentry vehicle[D]. Changsha: National University of Defense Technology, 2008(in Chinese). [8] TIAN B L, ZONG Q. 3DOF ascent phase trajectory optimization for aircraft based on adaptive Gauss pseudospectral method[C]// Proceedings of the 2012 Third International Conference on Intelligent Control and Information Processing. Piscataway: IEEE Press, 2012: 431-435. [9] 张宇翔. 固定翼无人机任务航迹规划及优化方法研究[D]. 杭州: 浙江大学, 2016.ZHANG Y X. Research on mission flight path planning and optimization method for Fixed-wing UAV[D]. Hangzhou: Zhejiang University, 2016(in Chinese). [10] HUANG J, LIU Z G, LIU Z Q, et al. A pk-adaptive mesh refinement for pseudospectral method to solve optimal control problem[J]. IEEE Access, 2019, 7: 161666-161679. doi: 10.1109/ACCESS.2019.2952139 [11] LIU G Q, LI B, JI Y D. A modified HP-adaptive pseudospectral method for multi-UAV formation reconfiguration[J]. ISA transactions, 2022, 129: 217-229. doi: 10.1016/j.isatra.2022.01.015 [12] CHAI R Q, SAVVARIS A, TSOURDOS A, et al. Trajectory optimization of space maneuver vehicle using a hybrid optimal control solver[J]. IEEE Transactions on Cybernetics, 2019, 49(2): 467-480. doi: 10.1109/TCYB.2017.2778195 [13] CHAI R Q, TSOURDOS A, SAVVARIS A, et al. Real-time reentry trajectory planning of hypersonic vehicles: a two-step strategy incorporating fuzzy multiobjective transcription and deep neural network[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6904-6915. doi: 10.1109/TIE.2019.2939934 [14] 李博雅, 李臻, 顾一凡, 等. 基于hp-自适应伪谱法的飞行器轨迹优化[C]//第十七届上海航天科技论坛暨上海市宇航学会2022学术年会论文集. 上海, 2023: 159-168.LI B Y, LI Z, GU Y F, et al. Aircraft trajectory optimization based on hp-adaptive pseudospectral method[C]//Proceedings of the 17th Shanghai Aerospace Science and Technology Forum and 2022 Annual Conference of the Shanghai Astronautics Society. Shanghai: SSA, 2023:159-168. [15] 黄斌. 基于hp自适应伪谱法的六自由度运动轨迹优化研究[D]. 南京: 南京航空航天大学, 2021: 16.HUANG B. Research on optimization of six-dof motion trajectory based on hp adaptive pseudospectral method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2021: 16(in Chinese). [16] 方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2005: 22-30.FANG Z P, CHEN W C, ZHANG S G. Flight dynamics of aircraft[M]. Beijing: Beijing University of Aeronautics & Astronautics Press, 2005: 22-30(in Chinese). [17] HOWE D, RORIE G. Aircraft conceptual design synthesis[M]. London: Professional Engineering Publishing, 2000. [18] VELÁSQUEZ-SANMARTÍN F, INSAUSTI X, ZÁRRAGA-RODRÍGUEZ M, et al. A mathematical model for the analysis of jet engine fuel consumption during aircraft climb and descent[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(5): 3605-3614. doi: 10.1109/TITS.2023.3333276 [19] HARGRAVES C R, PARIS S W. Direct trajectory optimization using nonlinear programming and collocation[J]. Journal of Guidance Control, and Dynamics, 1987, 10(4): 338-342. doi: 10.2514/3.20223 [20] BETTS J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207. doi: 10.2514/2.4231 [21] HUNTINGTON G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D]. Cambridge: Massachusetts Institute of Technology, 2007. [22] BENSON D A, HUNTINGTON G T, RAO V. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1435-1440. doi: 10.2514/1.20478 [23] GILL P E, MURRAY W, SAUNDERS M A. SNOPT: an SQP algorithm for large-scale constrained optimization[J]. SIAM Journal on Optimization, 2002, 12(4): 979-1006. doi: 10.1137/S1052623499350013 [24] DARBY C L, HAGER W W, RAO A V. An hp-adaptive pseudospectral method for solving optimal control problems[J]. Optimal Control Applications and Methods, 2011, 32(4): 476-502. doi: 10.1002/oca.957 [25] PATTERSON M A, HAGER W W, RAO A V. A ph mesh refinement method for optimal control[J]. Optimal Control Applications and Methods, 2015, 36(4): 398-421. doi: 10.1002/oca.2114 [26] LIU F J, HAGER W W, RAO A V. Adaptive mesh refinement method for optimal control using nonsmoothness detection and mesh size reduction[J]. Journal of the Franklin Institute, 2015, 352(10): 4081-4106. doi: 10.1016/j.jfranklin.2015.05.028 [27] RAO A V, BENSON D A, DARBY C, et al. Algorithm 902[J]. ACM Transactions on Mathematical Software, 2010, 37(2): 1-39. -
下载:
点击查看大图
计量
- 文章访问数: 194
- HTML全文浏览量: 60
- PDF下载量: 17
- 被引次数: 0
