基于灰色理论的复杂系统多故障模糊诊断

张弢; 王金波; 张涛; 王建敏

doi:10.13700/j.bh.1001-5965.2016.0703

基于灰色理论的复杂系统多故障模糊诊断

doi: 10.13700/j.bh.1001-5965.2016.0703

张弢^{1, 2, ,},
王金波¹,
张涛¹,
王建敏¹

1.
中国科学院空间应用工程与技术中心, 北京 100094
2.
中国科学院大学, 北京 100049

基金项目:

国家科技重大专项 Y3140731RN

详细信息

作者简介:
张弢  男, 博士研究生, 助理研究员; 主要研究方向:测试系统设计与故障诊断、软件评测

王金波  男, 博士, 副研究员; 主要研究方向:高可靠软件评测、测试系统设计

张涛  男, 博士, 研究员, 博士生导师; 主要研究方向:航天应用系统总体设计

王建敏  男, 博士, 助理研究员; 主要研究方向:自动控制技术、系统测试、软件评测

通讯作者:
张弢, E-mail:ztao@csu.ac.cn

中图分类号: V557⁺.2;TP206.3
计量
- 文章访问数: 747
- HTML全文浏览量: 176
- PDF下载量: 439
- 被引次数: 0
出版历程
- 收稿日期: 2016-09-02
- 录用日期: 2016-10-14
- 网络出版日期: 2017-09-20

Multi-fault fuzzy diagnosis for complicated system based on grey theory

1.
Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds:

National Science and Technology Major Project Y3140731RN

More Information

Corresponding author: ZHANG Tao, E-mail:ztao@csu.ac.cn

摘要

摘要:
航天、核电等复杂系统源发故障概率通常难于获取，由此导致基于最大后验概率准则的诊断方法失效。针对上述问题，从测试可靠性先验概率入手，提出了一种基于相关矩阵和灰色系统理论的故障诊断方法，通过对系统建立故障-测试相关矩阵，生成有排序的测试报警概率矩阵，并利用灰色关联度衡量测试结果向量与故障特征向量的接近度，实现了对多发故障的模糊诊断。实验结果表明，该方法在诊断指标权重调整、诊断精细度、重点关注故障检出等方面优势明显，诊断结论正确率满足实用需求。
- 模糊诊断 /
- 灰色关联分析 /
- 相关矩阵 /
- 概率推理 /
- 复杂系统
Abstract:
The failure probability is usually hard to collect for complicated systems in aerospace or nuclear power, which makes fault diagnosis based on Bayesian model inapplicable. By surveying this problem in test space, a novel multi-fault fuzzy diagnosis method based on dependency matrix and grey theory was proposed. A fault-testing dependency matrix was described first, and the fault alarm probability matrix with interest priority was developed. By calculating grey correlation degrees between test vectors and fault feature vectors, suspect faults can be located. Experimental results show that the proposed method can support diagnosis parameters' adjustment and report interested faults first, and the diagnosis conclusion has suitable accuracy, which can meet the practical demand.
- fuzzy diagnosis /
- grey correlation analysis /
- dependency matrix /
- probability reasoning /
- complicated system

HTML全文

图 1 示例系统有向信息流图

Figure 1. Directed information flow for sample system

下载: 全尺寸图片幻灯片

图 2 多故障模糊诊断的实施流程

Figure 2. Implementation process of multi-fault fuzzy diagnosis

下载: 全尺寸图片幻灯片

图 3 不同ε取值情况下故障状态5的灰色关联度

Figure 3. Grey correlation degrees of fault state 5 at different ε values

下载: 全尺寸图片幻灯片

图 4 表 5中故障状态的SCR取值

Figure 4. SCR values of fault states in Table 5

下载: 全尺寸图片幻灯片

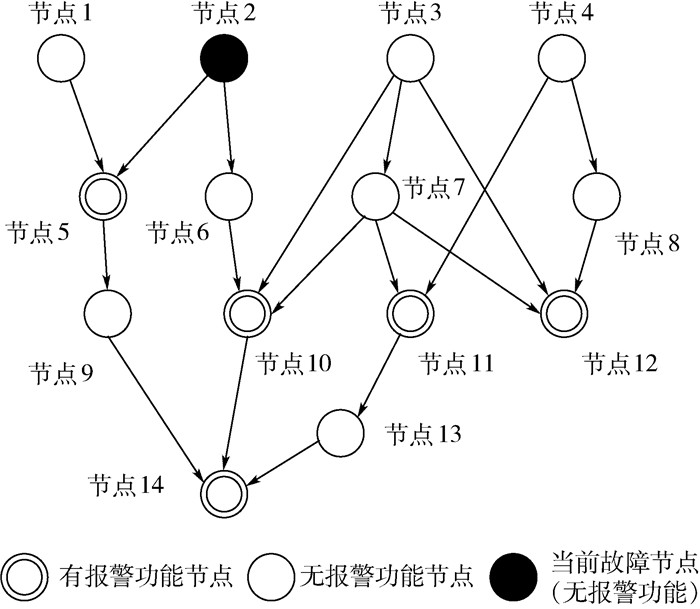
表 1 示例系统的D_FT矩阵

Table 1. D_FT matrix for sample system

故障节点	测试/报警节点号
故障节点	1/5	2/10	3/11	4/12	5/14
1	1	0	0	0	1
2	1	1	0	0	1
3	0	1	1	1	1
4	0	0	1	1	1
5	1	0	0	0	1
6	0	1	0	0	1
7	0	1	1	1	1
8	0	0	0	1	0
9	0	0	0	0	1
10	0	1	0	0	1
11	0	0	1	0	1
12	0	0	0	1	0
13	0	0	0	0	1
14	0	0	0	0	1

下载: 导出CSV

表 2 示例系统的P_AL矩阵

Table 2. P_AL matrix of sample system

故障节点	测试/报警节点号
故障节点	1/5	2/10	3/11	4/12	5/14
1	FDR₁₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR₁₅
2	FDR₂₁	FDR₂₂	FAR₃₃	FAR₃₄	FDR₂₅
3	FAR₃₁	FDR₃₂	FDR₃₃	FDR₃₄	FDR₃₅
4	FAR₃₁	FAR₃₂	FDR₄₃	FDR₄₄	FDR₄₅
5	FDR₅₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR₅₅
6	FAR₃₁	FDR₆₂	FAR₃₃	FAR₃₄	FDR₆₅
7	FAR₃₁	FDR₇₂	FDR₇₃	FDR₇₄	FDR₇₅
8	FAR₃₁	FAR₃₂	FAR₃₃	FDR₈₄	FAR₃₅
9	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR₉₅
10	FAR₃₁	FDR_{10, 2}	FAR₃₃	FAR₃₄	FDR_{10, 5}
11	FAR₃₁	FAR₃₂	FDR_{11, 3}	FAR₃₄	FDR_{11, 5}
12	FAR₃₁	FAR₃₂	FAR₃₃	FDR_{12, 4}	FAR₃₅
13	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR_{13, 5}
14	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR_{14, 5}

下载: 导出CSV

表 3 示例系统的P_EX矩阵

Table 3. P_EX matrix of sample system

故障节点	测试/报警节点号
故障节点	1/5	2/10	3/11	4/12	5/14
1	FDR₁₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR₁₅
1, 2	FDR₁₁	FDR₂₂	FAR₃₃	FAR₃₄	FDR₁₅
1, 3	FDR₁₁	FDR₃₂	FDR₃₃	FDR₃₄	FDR₁₅
					
1, 14	FDR₁₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR₁₅

2	FDR₂₁	FDR₂₂	FAR₃₃	FAR₃₄	FDR₂₅
2, 3	FDR₂₁	FDR₂₂	FDR₃₃	FDR₃₄	FDR₂₅
					
2, 14	FDR₂₁	FDR₂₂	FAR₃₃	FAR₃₄	FDR₂₅
					
13	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR_{13, 5}
13, 14	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR_{13, 5}

14	FAR₃₁	FAR₃₂	FAR₃₃	FAR₃₄	FDR_{14, 5}

下载: 导出CSV

表 4 阿波罗飞船发射前系统状态D_FT矩阵

Table 4. System state matrix D_FT before launch of Apollo spacecraft

故障节点	测试节点
故障节点	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	0	0	0	1	0	0	0	1	0	1	1	1	1	0	0
2	0	0	1	0	1	0	0	0	0	0	1	1	0	1	0
3	0	0	0	0	1	1	1	0	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	0	0	0	0	1	1
5	0	1	0	1	0	1	1	1	1	1	0	0	1	1	0
6	0	0	0	1	1	0	0	1	1	1	0	1	1	1	1
7	1	0	0	1	1	0	0	1	0	0	1	0	1	0	1
8	1	1	1	0	0	1	1	0	1	1	1	0	0	1	0
9	1	0	0	1	1	0	0	0	0	0	0	1	0	1	1
10	1	1	1	1	0	0	1	0	0	0	1	0	1	1	0

下载: 导出CSV

表 5 理想输入条件下的诊断结果

Table 5. Diagnosis results under ideal input condition

故障状态	报警传感器	文献[8]方法诊断结论				本文方法诊断结论
故障状态	报警传感器	输出排序	故障序号	诊断判据	判据结果	输出排序	故障序号	诊断判据	判据结果
1	4, 8, 10, 11, 12, 13	最可能	1	相似度	0.996 3	最可能	1	接近度	0.933 3
		次可能	1, 2	相似度	0.906 9	次可能	1, 2	接近度	0.805 3
		第三可能	1, 7	相似度	0.906 9	第三可能	1, 6	接近度	0.762 6
3	5, 6, 7, 9, 10, 11, 12, 15	最可能	3	相似度	0.997 8	最可能	3	接近度	0.911 1
		次可能	2, 3	相似度	0.946 1	次可能	2, 3	接近度	0.825 7
		第三可能	3, 4	相似度	0.946 1	第三可能	3, 4	接近度	0.825 7
5	2, 4, 6, 7, 8, 9, 10, 13, 14	最可能	5	相似度	0.998 3	最可能	5	接近度	0.900 0
		次可能	4, 5	相似度	0.973 2	次可能	4, 5	接近度	0.857 3
		第三可能	1, 5	相似度	0.951 4	第三可能	1, 5	接近度	0.814 6
7	1, 4, 5, 8, 11, 13, 15	最可能	7	相似度	0.997 2	最可能	7	接近度	1.000 0
		次可能	1, 7	相似度	0.939 5	次可能	1, 7	接近度	0.997 1
		第三可能	7, 9	相似度	0.939 5	第三可能	7, 9	接近度	0.997 1
9	1, 4, 5, 12, 14, 15	最可能	9	相似度	0.996 3	最可能	9	接近度	1.000 0
		次可能	2, 9	相似度	0.931 1	次可能	2, 9	接近度	0.997 1
		第三可能	4, 9	相似度	0.906 9	第三可能	4, 9	接近度	0.995 7
2, 4	2, 3, 5, 6, 7, 11, 12, 14, 15	最可能	2, 4	相似度	0.998 3	最可能	2, 4	接近度	0.900 0
		次可能	3, 8	相似度	0.932 5	次可能	2, 3	接近度	0.781 4
		第三可能	2, 3	相似度	0.925 8	第三可能	3, 4	接近度	0.781 4
4, 6	2, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15	最可能	4, 6	相似度	0.999 4	最可能	4, 6	接近度	0.866 7
		次可能	5, 6	相似度	0.999 4	次可能	5, 6	接近度	0.866 7
		第三可能	3, 5	相似度	0.980 0	第三可能	3, 5	接近度	0.824 0
6, 8	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15	最可能	6, 8	相似度	1.000 0	最可能	6, 8	接近度	1.000 0
		次可能	3, 10	相似度	0.986 3	次可能	3, 10	接近度	0.998 6
		第三可能	6, 10	相似度	0.986 3	第三可能	6, 10	接近度	0.998 6
8, 10	1, 2, 3, 4, 6, 7, 9, 10, 11, 13, 14	最可能	8, 10	相似度	0.999 1	最可能	8, 10	接近度	1.000 0
		次可能	5, 8	相似度	0.978 1	次可能	5, 8	接近度	0.998 6
		第三可能	5, 10	相似度	0.978 1	第三可能	5, 10	接近度	0.998 6
1, 10	1, 2, 3, 4, 7, 8, 10, 11, 12, 13, 14	最可能	1, 10	相似度	0.999 1	最可能	1, 10	接近度	1.000 0
		次可能	1, 8	相似度	0.959 6	次可能	1, 8	接近度	0.997 1
		第三可能	6, 10	相似度	0.943 0	第三可能	2, 10	接近度	0.995 7

下载: 导出CSV

表 6 故障组合(1, 10) 的接近度量值与候选诊断结论示例

Table 6. Example of approximate measurement value and candidate diagnosis result of fault combination (1, 10)

接近度量值	候选诊断结论(疑似故障/故障组合)
0.995 7	2, 10	5, 8	5, 10	6, 10	10

下载: 导出CSV

参考文献(18)

[1]	HASHTRUDIZAD S, KWONG R H, WONHAM W M.Fault diagnosis in discrete-event systems:Framework and model reduction[J].IEEE Transactions on Automatic Control, 2003, 48(7):1199-1212. doi: 10.1109/TAC.2003.814099
[2]	田仲, 石君友.系统测试性设计分析和验证[M].北京:北京航空航天大学出版社, 2003:4-8. TIAN Z, SHI Z Y.System testability design analysis and verification[M].Beijing:Beihang University Press, 2003:4-8(in Chinese).
[3]	DE PAUL R.A logic modeling as a tool for testability[C]//Proceedings of IEEE International Automatic Testing Conference.Piscataway, NJ:IEEE Press, 1985:203-207.
[4]	DEB S, PATTIPATI K R, RAGHAVAN V.Multi-signal flow graphs:A novel approach for system testability analysis and fault diagnosis[J].IEEE Aerospace & Electronic Systems Magazine, 1995, 10(5):14-25.
[5]	RAO N S V.On parallel algorithms for single-fault diagnosis in fault propagate on graph systems[J].IEEE Transactions on Parallel and Distributed Systems, 1996, 7(12):1217-1223. doi: 10.1109/71.553268
[6]	KOKAWA M, MIYAZAKI S, SHINGAI S.Fault location using digraph and inverse direction search with application[J].Automatic, 1983, 19(6):729-735. doi: 10.1016/0005-1098(83)90039-0
[7]	尹园威, 尚朝轩, 马彦恒, 等.层次测试性模型的评估方法[J].北京航空航天大学学报, 2015, 41(1):90-95. http://bhxb.buaa.edu.cn/CN/abstract/abstract13130.shtml YIN Y W, SHANG C X, MA Y H, et al.Method of testability evaluation using hierarchical testability model[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1):90-95(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13130.shtml
[8]	连可, 黄建国, 龙兵.一种基于有向图模型的模糊多故障诊断算法[J].系统工程与电子技术, 2008, 30(3):568-571. http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200803047.htm LIAN K, HUANG J G, LONG B.Fuzzy multiple fault diagnosis algorithm based on digraph models[J].Systems Engineering and Electronics, 2008, 30(3):568-571(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200803047.htm
[9]	杨鹏, 邱静, 刘冠军.基于扩展的关联模型的测试性分析技术研究[J].系统工程与电子技术, 2008, 30(2):371-374. http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200802045.htm YANG P, QIU J, LIU G J.Research on extended dependency model-based testability analysis[J].Systems Engineering and Electronics, 2008, 30(2):371-374(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200802045.htm
[10]	梁爽, 于劲松, 唐荻音, 等.基于多信号流图与分支定界算法的故障诊断[J].北京航空航天大学学报, 2016, 42(1):180-186. http://bhxb.buaa.edu.cn/CN/abstract/abstract13689.shtml LIANG S, YU J S, TANG D Y, et al.Research on fault diagnosis based on multi-signal flow graph and branch and bound algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1):180-186(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13689.shtml
[11]	方甲永, 肖明清, 王学奇, 等.测试不可靠条件下多故障诊断方法[J].北京航空航天大学学报, 2011, 37(4):433-438. http://bhxb.buaa.edu.cn/CN/abstract/abstract11938.shtml FANG J Y, XIAO M Q, WANG X Q, et al.Multiple fault diagnosis method with unreliable test[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4):433-438(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract11938.shtml
[12]	沈琳, 于劲松, 唐荻音, 等.图模型与学习算法结合的贝叶斯网络自动建模[J].北京航空航天大学学报, 2016, 42(7):1486-1493. http://bhxb.buaa.edu.cn/CN/abstract/abstract13478.shtml SHEN L, YU J S, TANG D Y, et al.Automatic learning of Bayesian network structure using graph model and learning algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7):1486-1493(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13478.shtml
[13]	SHAKERI M, RAGHAVAN V, PATTIPATI K R, et al.Sequential testing algorithms for multiple fault diagnosis[J].IEEE Transactions on Systems, Man and Cybernetics, 2000, 30(1):1-14. http://www.academia.edu/25189253/Sequential_testing_algorithms_for_multiple_fault_diagnosis
[14]	U.S.Department of Defense.Basic dependency modeling terminology[EB/OL].Washington, D.C.:Office of the Secretary of Defense, DoD, 2008(2008-06-16)[2016-09-02].http://www.testability.com/Reference/Glossaries.aspx?Glossary=DependencyModeling.
[15]	CHESSA S, SANTI P.Operative diagnosis of graph-based systems in multiple faults[J].IEEE Transactions on Systems, Man and Cybernetics, 2001, 31(2):112-119. doi: 10.1109/3468.911368
[16]	DENG J L.Introduction to grey system theory[J].Journal of Grey System, 1989, 1(1):1-24.
[17]	刘思峰, 杨英杰, 吴利丰, 等.灰色系统理论及其应用[M].北京:科学出版社, 2014:63-75. LIU S F, YANG Y J, WU L F, et al.The grey system theory and its application[M].Beijing:Science Press, 2014:63-75(in Chinese).
[18]	WOHL J G.Information automation and the Apollo program:A retrospective[J].IEEE Transactions on Systems, Man and Cybernetics, 1982, 12(4):469-478. doi: 10.1109/TSMC.1982.4308851