基于脱靶量级数解的最优机动突防策略

王亚帆; 周韬; 陈万春; 赫泰龙

doi:10.13700/j.bh.1001-5965.2019.0135

基于脱靶量级数解的最优机动突防策略

doi: 10.13700/j.bh.1001-5965.2019.0135

北京航空航天大学宇航学院, 北京 100083

详细信息

作者简介:
王亚帆, 女, 硕士研究生。主要研究方向:导弹制导与控制

周韬, 男, 硕士, 副教授, 硕士生导师。主要研究方向:导弹总体设计与仿真、导弹制导与控制

陈万春, 男, 博士, 教授, 博士生导师。主要研究方向:飞行力学、导弹制导与控制

通讯作者:
陈万春, E-mail:wanchun_chen@buaa.edu.cn

中图分类号: V221⁺.3;TB553
计量
- 文章访问数: 864
- HTML全文浏览量: 135
- PDF下载量: 368
- 被引次数: 0
出版历程
- 收稿日期: 2019-04-01
- 录用日期: 2019-08-30
- 网络出版日期: 2020-01-20

Optimal maneuver penetration strategy based on power series solution of miss distance

School of Astronautics, Beihang University, Beijing 100083, China

More Information

Corresponding author: CHEN Wanchun, E-mail:wanchun_chen@buaa.edu.cn

摘要

摘要:
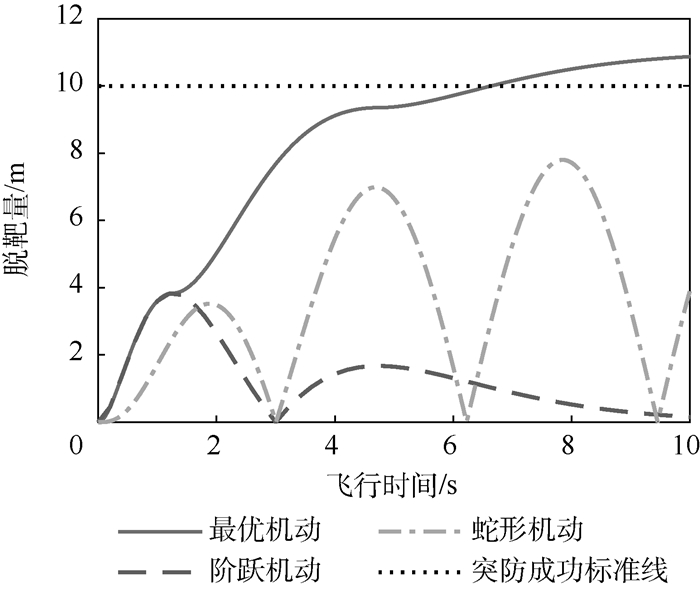
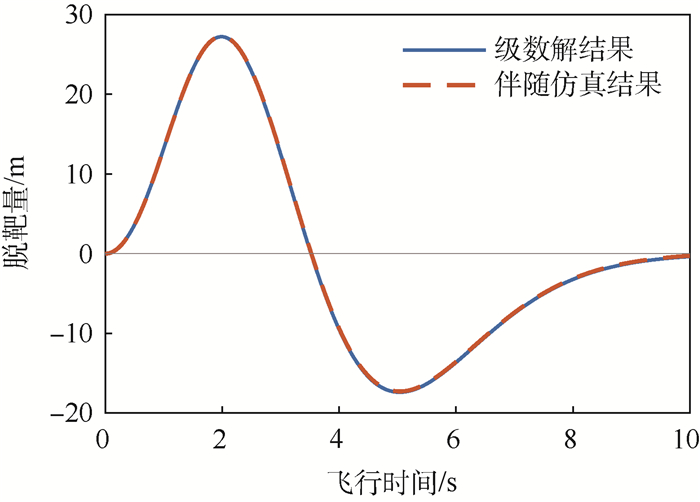
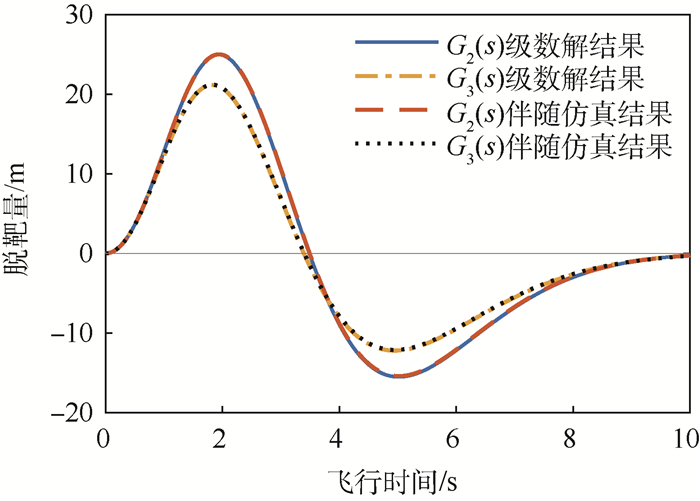
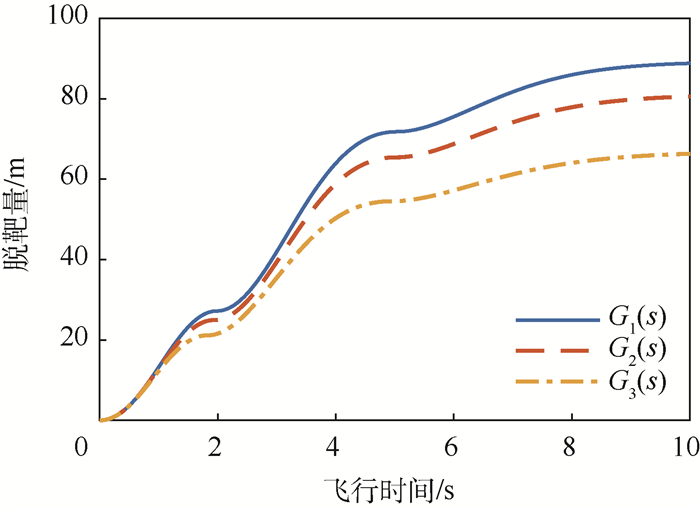
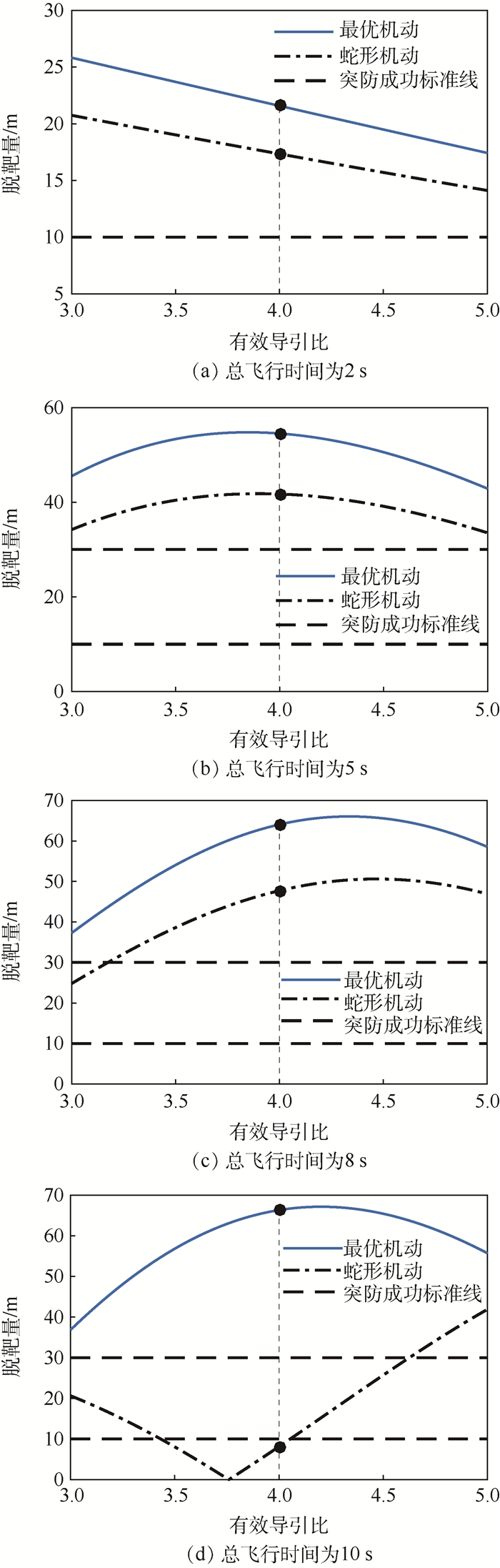
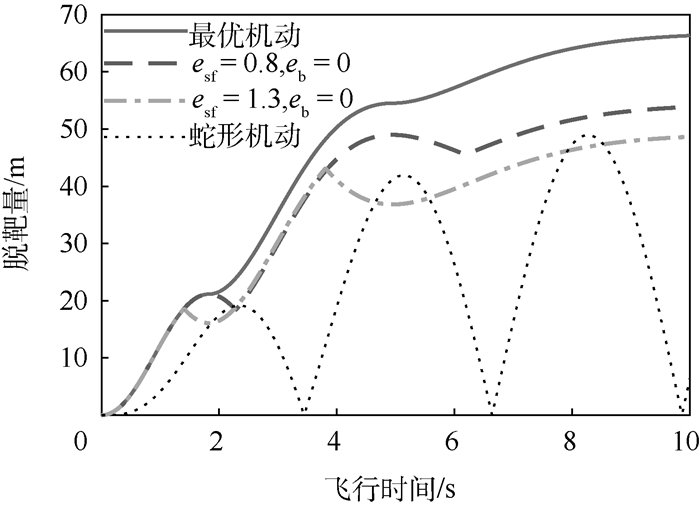
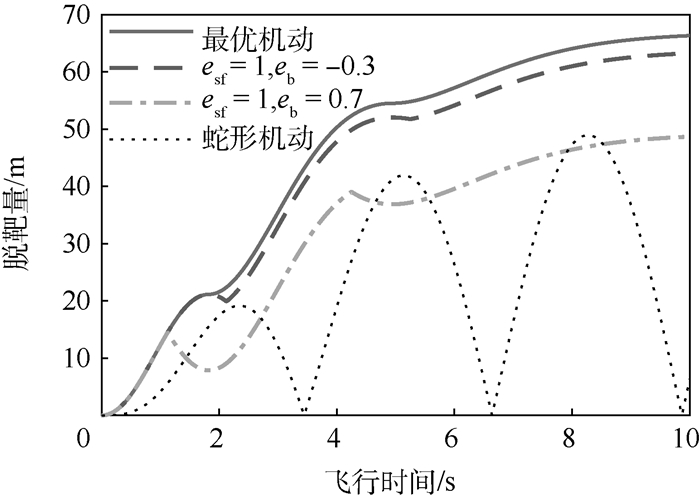
针对比例导引控制的拦截弹，建立高阶制导系统状态空间模型，基于脱靶量级数解公式，对目标最优机动突防策略及其影响因素进行了研究。首先，针对拦截弹的制导系统为线性一阶、线性高阶时，目标最优机动突防效果进行了仿真分析，结果表明拦截弹弹体模型的准确性对突防效果存在影响，高阶系统对应脱靶量更大且效果更真实；将结果与一次阶跃机动和蛇形机动对比，发现最优机动突防效果最佳。然后，建立弹目运动的二维非线性模型，仿真得出目标最优机动产生的脱靶量曲线与线性系统吻合度较高，线性模型选取合适。最后，研究了有效导引比和剩余飞行时间估计误差对最优机动突防效果产生的影响，结果表明有效导引比估计误差对最优机动突防效果影响不大，剩余飞行时间估计误差则会使目标最优机动突防性能大幅下降，甚至部分情况比蛇形机动突防效果差。
- 突防 /
- 最优机动 /
- 脱靶量级数解 /
- 估计误差 /
- 伴随法 /
- 仿真分析
Abstract:
Aimed at the proportional guidance missile, the state space model of high-order guidance system was established, and the optimal maneuver penetration strategy and influencing factors were studied based on power series solution of miss distance. First, when the missile guidance system was linear first-order and high-order, the simulations of optimal target maneuver penetration were carried out. The results show that the accuracy of the missile guidance model has an impact on the penetration effect, and the high order has larger miss distance and is more realistic. Then, the results were compared with step maneuver and weaving maneuver, the optimal maneuver penetration effect is the best. Furthermore, a two-dimensional nonlinear missile-target engagement model was established, and the simulation shows that the miss distance curve of optimal maneuver is highly identical with the linear system, and the linear system is selected appropriately. Finally, the impacts of effective navigation ratio and time-to-go estimation error on the optimal maneuver penetration effect were studied. The effective navigation ratio estimation error has little effect on the optimal maneuver penetration effect, the time-to-go estimation error makes the target optimal maneuver penetration performance decline greatly, and in some cases it is even worse than the weaving maneuver penetration effect.
- penetration /
- optimal maneuver /
- power series solution of miss distance /
- estimation error /
- adjoint method /
- simulation analysis

HTML全文

图 1 一阶系统目标最优机动突防(N=4)

Figure 1. Target optimal maneuver penetration of first-order system (N=4)

下载: 全尺寸图片幻灯片

图 2 一阶系统目标机动产生脱靶量对比曲线(N=4)

Figure 2. Miss distance contrast curves of first-order system for target maneuver (N=4)

下载: 全尺寸图片幻灯片

图 3 五阶二项式系统目标阶跃机动产生脱靶量级数解与伴随仿真结果对比曲线

Figure 3. Contrast curves between miss distance power series solutions of fifth-order binomial system due to target step maneuver and adjoint simulation results

下载: 全尺寸图片幻灯片

图 4 五阶二项式系统目标机动产生脱靶量对比曲线

Figure 4. Miss distance contrast curves of fifth-order binomial system for target maneuver

下载: 全尺寸图片幻灯片

图 5 高阶系统目标阶跃机动产生脱靶量级数解与伴随仿真结果对比曲线

Figure 5. Contrast curves between miss distance power series solutions of high-order system due to target step maneuver and adjoint simulation results

下载: 全尺寸图片幻灯片

图 6 高阶系统目标最优机动脱靶量对比曲线

Figure 6. Miss distance contrast curves of high-order systems for target optimal maneuver

下载: 全尺寸图片幻灯片

图 7 线性最优机动和非线性最优机动脱靶量对比

Figure 7. Miss distance comparison between linear and nonlinear optimal maneuver

下载: 全尺寸图片幻灯片

图 8 有效导引比存在估计误差时目标机动产生脱靶量

Figure 8. Target maneuver miss distance when effective navigation ratio estimation error exists

下载: 全尺寸图片幻灯片

图 9 高阶系统目标最优机动突防(G₃(s)，N=4)

Figure 9. Target optimal maneuver penetration of high-order system (G₃(s), N=4)

下载: 全尺寸图片幻灯片

图 10 目标最优机动脱靶量关于剩余飞行时间标度系数误差的曲线

Figure 10. Curves of target optimal maneuver miss distance relative to scale factor error of time to go

下载: 全尺寸图片幻灯片

图 11 标度系数误差存在时目标最优机动产生脱靶量

Figure 11. Target optimal maneuver miss distance when scale factor error exists

下载: 全尺寸图片幻灯片

图 12 目标最优机动脱靶量关于剩余飞行时间零偏误差的曲线

Figure 12. Curve of target optimal maneuver miss distance relative to bias error of time to go

下载: 全尺寸图片幻灯片

图 13 零偏误差存在时目标最优机动产生脱靶量

Figure 13. Target optimal maneuver miss distance when bias error exists

下载: 全尺寸图片幻灯片

表 1 一阶系统最优控制切换时刻及最大脱靶量

Table 1. Optimal control switching time and maximum miss distance of first-order system

N	t_go/s	w(t_go)/m	M_max/m
3	2.00	7.96	15.85
4	1.27	3.84	10.87
4	4.73	-1.67	10.87
5	0.94	2.27	8.45
	3.31	-1.73
	7.76	0.32

下载: 导出CSV

表 2 传递函数系数

Table 2. Transfer function coefficient

传递函数	系数取值
G₂(s)	α₁=0.066 7, α₂=0.133, α₃=0.2, α₄=0.267, α₅=0.333
G₃(s)	α₁=0.1, α₂=0.2, α₃=0.56, β=0.1, ξ=0.7

下载: 导出CSV

表 3 弹目仿真参数

Table 3. Simulation parameter of missile and target

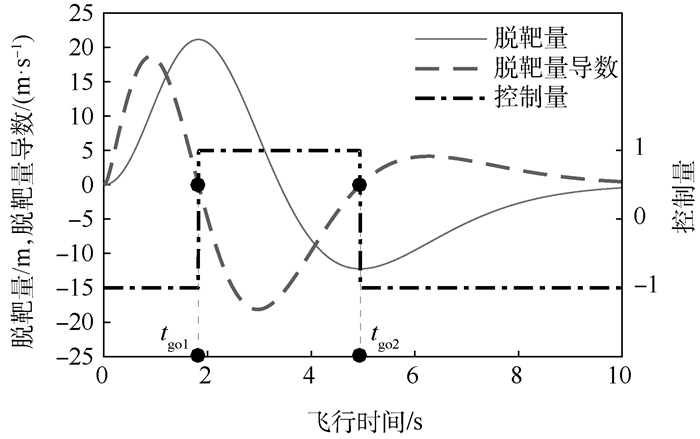
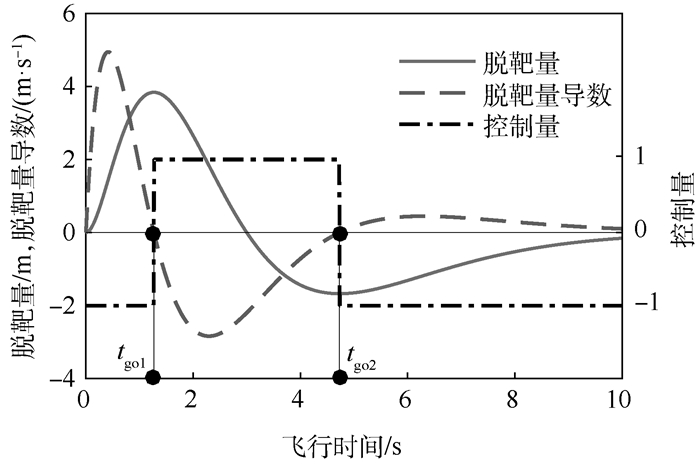
弹目	初始速度/(m·s^-1)	初始高度/m	初始水平位置/m	控制切换时刻
导弹	915	3 050	0
目标	305	3 050	(0, 122 00]	t_go1=1.82 s, t_go2=4.94 s
注：总飞行时间为[0, 10]s。

下载: 导出CSV

表 4 标度系数误差变化时目标最优机动产生脱靶量(t_f=10 s)

Table 4. Target optimal maneuver miss distance when scale factor error changes (t_f=10 s)

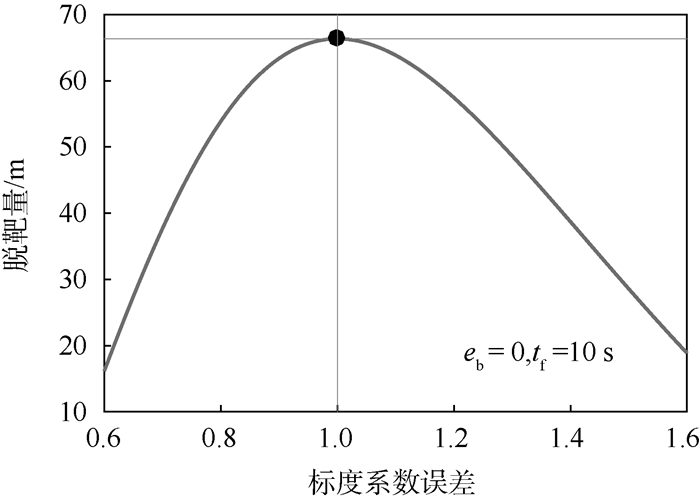
e_sf	t_go/s	M_max/m
0.8	t_go1=2.28，t_go2=6.19	53.87
1.0	t_go1=1.82, t_go2=4.94	66.33
1.3	t_go1=1.40, t_go2=3.81	48.64

下载: 导出CSV

表 5 零偏误差变化时目标最优机动产生脱靶量(t_f=10 s)

Table 5. Target optimal maneuver miss distance when bias error changes (t_f=10 s)

e_b	t_go/s	M_max/m
-0.3	t_go1=2.12，t_go2=5.24	63.26
0	t_go1=1.82，t_go2=4.94	66.33
0.7	t_go1=1.12, t_go2=4.24	48.70

下载: 导出CSV

参考文献(18)

[1]	WEISS M.Adjoint method for missile performance analysison state-space models[J].Journal of Guidance, Control and Dynamics, 2005, 28(2):236-248. doi: 10.2514/1.7342
[2]	ZARCHAN P.Tactical and strategic missile guidance[M].6th ed.Reston:AIAA, 2012:35-105.
[3]	LANING J H, BATTIN R H.Random processes in autmatic control[M].New York:McGraw-Hill Book Company, Inc., 1956:225-253.
[4]	BENASHER J Z.Application to missile guidance:Proportional navigation[M].Reston:AIAA, 2010:231-239.
[5]	NESLINE F W, ZARCHAN P.A new look at classical vs modern homing missile guidance[J].Journal of Guidance, Control, and Dynamics, 2012, 4(1):78-85. http://cn.bing.com/academic/profile?id=50b72877a6f170e4e3d792bf57ed3f1d&encoded=0&v=paper_preview&mkt=zh-cn
[6]	高雁翎, 张保庆.2017年世界弹道导弹防御发展分析[J].战术导弹技术, 2018(1):42-46. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zsddjs201801007 GAO Y L, ZHANG B Q.2017 world ballistic missile defense development analysis[J].Tactical Missile Technology, 2018(1):42-46(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zsddjs201801007
[7]	郑玉航, 于海燕, 孙鹏.导弹突防策略与措施研究[J].国防技术基础, 2002(5):46-48. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK200201670536 ZHENG Y H, YU H Y, SUN P.Study on missile penetration strategies and measures[J].Technology Foundation of National Defence, 2002(5):46-48(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK200201670536
[8]	ZARCHAN P.Proportional navigation and weaving targets[J].Journal of Guidance, Control, and Dynamics, 1995, 18(5):969-974. doi: 10.2514/3.21492
[9]	雍恩米, 唐国金, 罗亚中.弹道导弹中段机动突防制导问题的仿真研究[J].导弹与航天运载技术, 2005(4):13-18. doi: 10.3969/j.issn.1004-7182.2005.04.003 YONG E M, TANG G J, LUO Y Z.Research on maneuvering penetration guidance law of ballistic missile in middle-course flight by simulation method[J].Missiles and Space Vehicles, 2005(4):13-18(in Chinese). doi: 10.3969/j.issn.1004-7182.2005.04.003
[10]	SAILARANTA T, SILTAVUORI A, PANKKONEN A. Simple missile models against high-g barrel roll maneuver: AIAA-2011-6570[R].Reston: AIAA, 2011.
[11]	SHINAR J, STEINBERG D.Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model[J].Journal of Aircraft, 1977, 14(8):795-802. doi: 10.2514/3.58855
[12]	迟泽晨, 李长文, 王健.临近空间导弹最优机动突防控制策略研究[C]//中国空天安全会议, 2017. CHI Z C, LI C W, WANG J.Analysis of optimal evasive maneuvers control in near-space[C]//China Space Security Conference, 2017(in Chinese).
[13]	DHANANJAY N, GHOSE D.Accurate time-to-go estimation for proportional navigation guidance[J].Journal of Guidance, Control, and Dynamics, 2014, 37(4):1378-1383. doi: 10.2514/1.G000082
[14]	庄志洪, 涂建平, 王宏波.导弹目标遭遇过程中的剩余飞行时间估计[J].宇航学报, 2002, 23(5):32-38. doi: 10.3321/j.issn:1000-1328.2002.05.007 ZHUANG Z H, TU J P, WANG H B.Prediction of time to go during missile-target encounter[J].Journal of Astronautics, 2002, 23(5):32-38(in Chinese). doi: 10.3321/j.issn:1000-1328.2002.05.007
[15]	HE T L, CHEN W C.A new interpretation of adjoint method in linear time-varying system analysis[C]//IEEE International Conference on CIS & RAM.Piscataway, NJ: IEEE Press, 2017: 58-63.
[16]	赫泰龙, 陈万春, 周浩.高阶线性比例制导系统脱靶量幂级数解[J].航空学报, 2018, 39(11):322241. http://d.old.wanfangdata.com.cn/Periodical/hkxb201811015 HE T L, CHEN W C, ZHOU H.Power series solution for miss distance of higher-order linear proportional navigation guidance systems.[J].Acta Aeronautica et Astronautica Sinica, 2018, 39(11):322241(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hkxb201811015
[17]	SPEYER J L, JACOBSON D H.Primer on optimal control theory[M].Philadelphia:Society for Industrial and Applied Mathematics, 2010:79-83.
[18]	MURTAUGH S A, CRIEL H E. Fundamentals of proportional navigation[J]. Spectrum IEEE, 1966, 3(12):75-85. doi: 10.1109/MSPEC.1966.5217080