-
摘要:
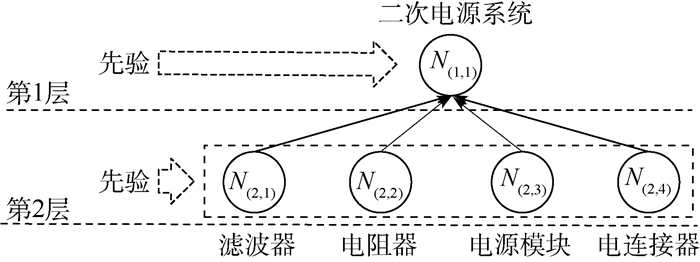
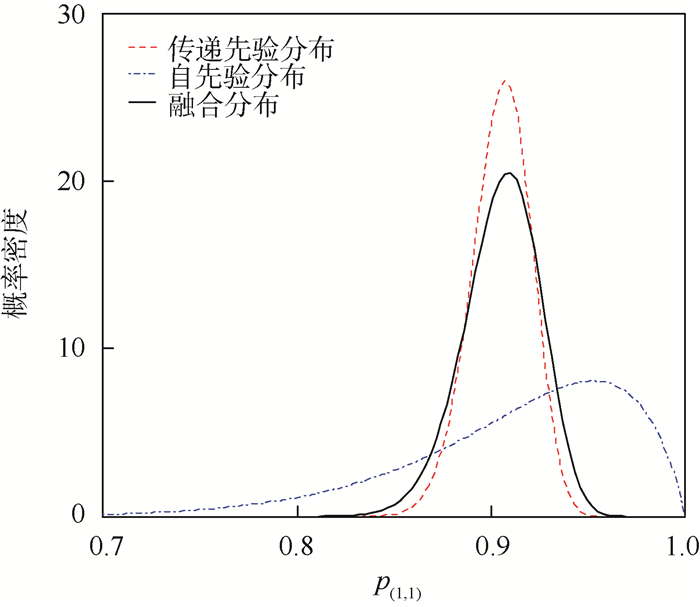
针对当前测试性验证领域未能考虑故障样本量确定和样本分配2个环节的相互联系，以及现有样本分配方案对影响因子的选择没有统一的框架，导致确定的故障样本量和样本分配不合理的问题，提出了一种故障样本量确定与分配一体化设计方案。首先，以层次Bayes网络模型为框架，融合各节点测试性指标先验信息得到顶层测试性指标的融合分布，并建立故障样本量确定流程；其次，引入结构重要度作为样本分配影响因子，同时结合故障模式影响及危害性分析（FMECA）信息确定节点和故障模式的样本分配影响因子，提出基于节点和故障模式的二次分配框架实施样本分配；最后，通过实际案例进行对比分析。结果表明：相比其他样本分配方案，所提方案能充分考虑系统结构及其先验信息，进而实现了故障样本量确定和分配一体化方案的设计，保证了所确定的故障样本量和分配的合理性，具备更好的工程适用性。
Abstract:For the current testability verification field, the relationship between the fault sample size determination and the sample allocation is not taken into consideration, and the existing sample allocation schemes have no uniform framework for the selection of the impact factor, which lead to the problem that the determined sample size and sample allocation are unreasonable, so an integrated design scheme for fault sample size determination and allocation is proposed. Firstly, the prior information of each node's testability indicators was integrated to obtain the fusion distribution of top-level testability indicators, which could be used to establish a fault sample size determination process based on the hierarchical Bayes network model. Secondly, the structural importance was introduced as the sample allocation influence factor. At the same time, the failure modes, effect and criticality analysis (FMECA) information was used to determine the sample allocation influence factor of the nodes and the failure modes. Then the secondary allocation framework based on the nodes and failure modes was proposed to implement the sample allocation. Finally, a comparative analysis was carried out through actual cases. The results show that, compared with other sample allocation schemes, the proposed scheme can fully consider the system structure and its prior information, and realize the integrated design for fault sample size determination and allocation, which ensures the reasonable sample size and allocation with better engineering applicability.
-
采用基于传统均匀网格的数值计算方法对含金属薄膜的大尺寸低剖面周期结构进行处理时往往面临着一大挑战，即应设置足够小的网格来捕捉导电薄层内的场变化。细微的离散化网格产生了大量的计算数据，也直接导致了较长的运算时间，同时，其还对计算机的内存和处理速度都提出了较高要求。目前，国内外研究机构已经提出了一些方法[1-12]来解决上述问题：①将亚网格技术用于薄层的细微网格建模[1-2]。但是，为保证方法的稳定性，离散时间步长仍受限制，这依然会导致大量的计算时间。②共形时域有限差分(FDTD)方法将导电薄层视为完美导体(PEC)，薄层上的切向场被设置为零[3-5]。在这种方法中，忽略导体损耗的这一处理可能会导致计算错误，尤其当结构处于高频电磁场时，导体将产生明显损耗。③采用表面阻抗边界条件(SIBC)直接分析金属薄层，可避免细微FDTD网格在薄层内部离散化的过程[6-9]。但在这种方法中，需要复杂的卷积处理和高精度的有理逼近运算。另外，Feliziani[10]提出了解决屏蔽问题的亚元胞FDTD模型，其优点是使用电路理论而不是使用卷积方程来求解屏蔽的场方程，虽然有效解决了屏蔽问题，但是对于复杂的结构(如多层板)，仍需要高精度的有理近似。Nayyeri[11]和Bouzianas[12]等提出了对石墨烯结构进行数值计算的方法，对石墨烯表面电导率方程进行直接分析，通过拉普拉斯变换和中心微分法将其结合到FDTD方法中进行建模运算。
本文提出了一种精确有效的方法来处理低剖面周期结构。通过拉普拉斯变换和中心微分法，将周期结构的Y矩阵参数直接嵌入到电场的更新方程中。与早期的工作相比，该方法可以对整体结构直接采用粗网格建模，时间步将不再受金属层厚度的限制；可以避免复杂的频域至时域的卷积运算，相关的频域函数可以由矢量拟合法轻松获得；计算时间快，精度高。
1. INBC-FDTD步进公式推导
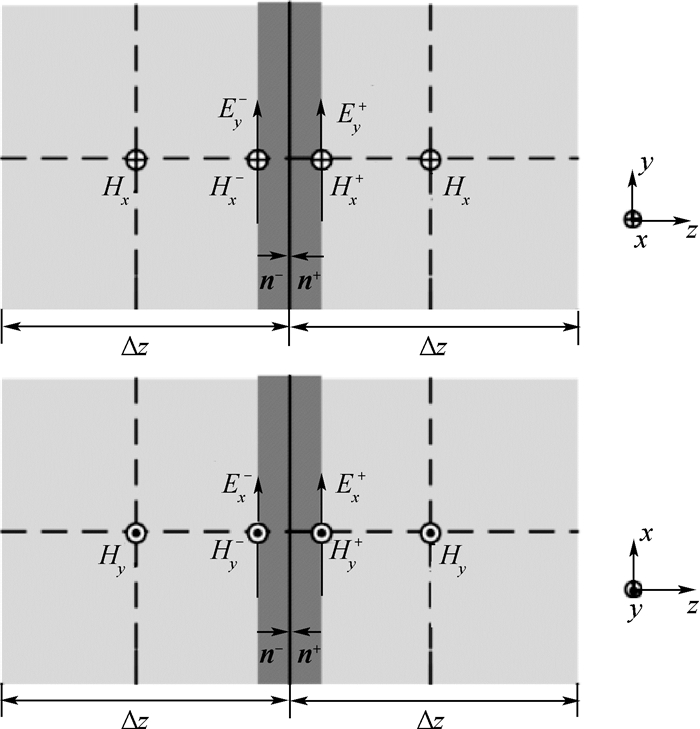
图 1给出了低剖面周期结构置于两FDTD网格Γ-和Γ+之间的侧视图。图中：n-和n+分别为由Γ-指向Γ+的向量和由Γ+指向Γ-的向量。假设该结构沿着z方向上的厚度远小于所关注的最高频段下的波长和结构的横向尺寸，则结构切向电场和切向磁场之间的关系可通过引入如下Y矩阵得到：
(1a) 
(1b) 
图 1 置于两FDTD网格Γ-和Γ+之间的低剖面周期结构侧视图Figure 1. Side view of low-profile periodic structure placed between two FDTD grids Γ-and Γ+式中：s=jω；Y11和Y22分别为Γ-和Γ+的自导纳，Y12和Y21分别为Γ-和Γ+的互导纳。
通过将式(1a)和式(1b)写为一系列表达式，可得
(2a) 
(2b) 
(2c) 
(2d) 在式(2a)~式(2d)中，与频率相关的Y矩阵系数Y11(s)、Y12(s)、Y21(s)和Y22(s)可以通过矢量拟合法[13]近似为由实数或共轭复数组成的有理分式之和，表示为
(3a) 
(3b) 式中：pn和rn分别为极点和留数，其值可为实数或者共轭复数；d为实数；N为极点的个数。
为了便于简单分析，仅对式(1a)作进一步推导。通过将式(3a)和式(3b)代入式(2a)和式(2b)，得到
(4a) 
(4b) 引入状态方程Xn, Y11(s)、Xn, Y12(s)、Xn, Y21(s)和Xn, Y22(s)：
(4c) 
(4d) 表达式(4c)和式(4d)可重写为
(5a) 
(5b) 
(5c) 
(5d) 上述表达式(5a)~式(5d)可以通过拉普拉斯变换
(6a) 
(6b) 
(6c) 
(6d) 式中：Δt为采样时间。
将式(5a)和式(5b)转换至离散时域，其在时刻为k+1/2的表达式为
(7a) 
(7bs) 通过将式(7a)~式(7b)代入至FDTD的电场Ey+k+1和Ey-k+1时域步进公式[14]，可以得到内部阻抗边界条件(INBC)的离散时域表达式为
(8a) 
(8b) 式中：
(9a) 
(9b) 
(9c) 
(9d) 其中：Δx、Δy和Δz分别为沿x、y和z的空间步长；i、j和k分别为FDTD电场和磁场的空间坐标；ε0为自由空间的介电常数。
总体来说，INBC-FDTD方法的场更新步骤可归纳如下：
步骤1 更新状态函数式(6a)~式(6d)。
步骤2 使用式(9c)和式(9d)更新系数F1y和F2y。
步骤3 使用式(8a)和式(8b)更新电场Ey-k+1和Ey+k+1。
Ex+k+1和Ex-k+1的时域步进公式可以按照以上方法作类似推导。对于磁场的时域步进公式，仍采用常规的FDTD公式进行计算。
2. 二维周期结构计算空间
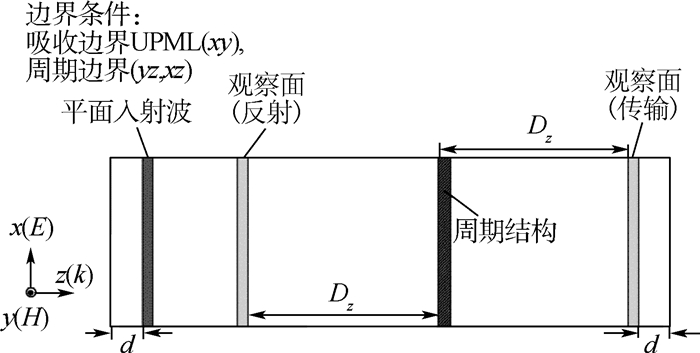
对于二维周期结构，当采用FDTD方法对其进行计算空间离散建模时，由于其在二维方向的周期性，大尺寸多周期的二维结构的模型可以等效为二维周期延拓方向均设置周期边界的一个周期单元。图 2给出了二维周期结构的计算空间示意图。可以看出，沿着二维周期延拓方向设置垂直的周期边界，各向异性完美匹配层(UPML)吸收边界平行于周期结构表面。吸收边界通过设定吸收边界上的入射电压为0，即可正确地模拟无反射截断边界条件。
图 2 二维周期结构的计算空间示意图Figure 2. Schematic diagram of computational space for two-dimensional periodic structure因为FDTD方法是基于时间和空间的离散方法，需要选择空间观察面/点来记录入射或反射时域波形。通过给定入射平面波激励：
(10) 可以观察入射、反射和透射波形，通过对时域波形进行时频转换，可以得到入射、反射及透射波形的频谱图。通过
(11) 可以计算得到该结构的频域反射和透射系数。式中：fref(s)、ftran(s)和finc(s)分别为反射波、透射波和入射波的频域函数。
3. 数值计算与分析
基于对INBC-FDTD方法的详细推导，本节给出2个计算实例，用于验证所提方法的正确性和高效性。采用如图 2所示的计算空间，其中吸收边界UPML与入射波边界的距离设为10个元胞的距离，另外，观察面与低剖面周期结构的距离Dz设置为30个网格。
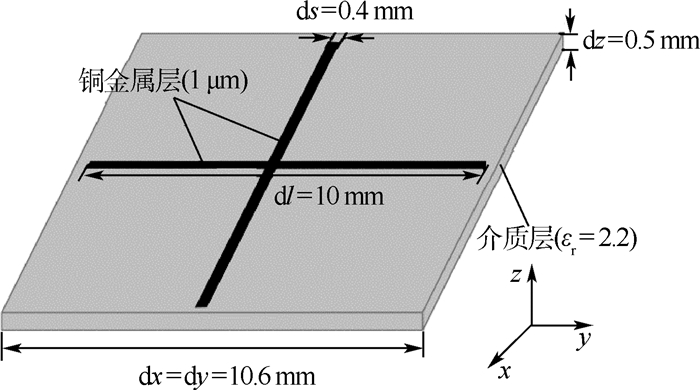
3.1 十字贴片型FSS
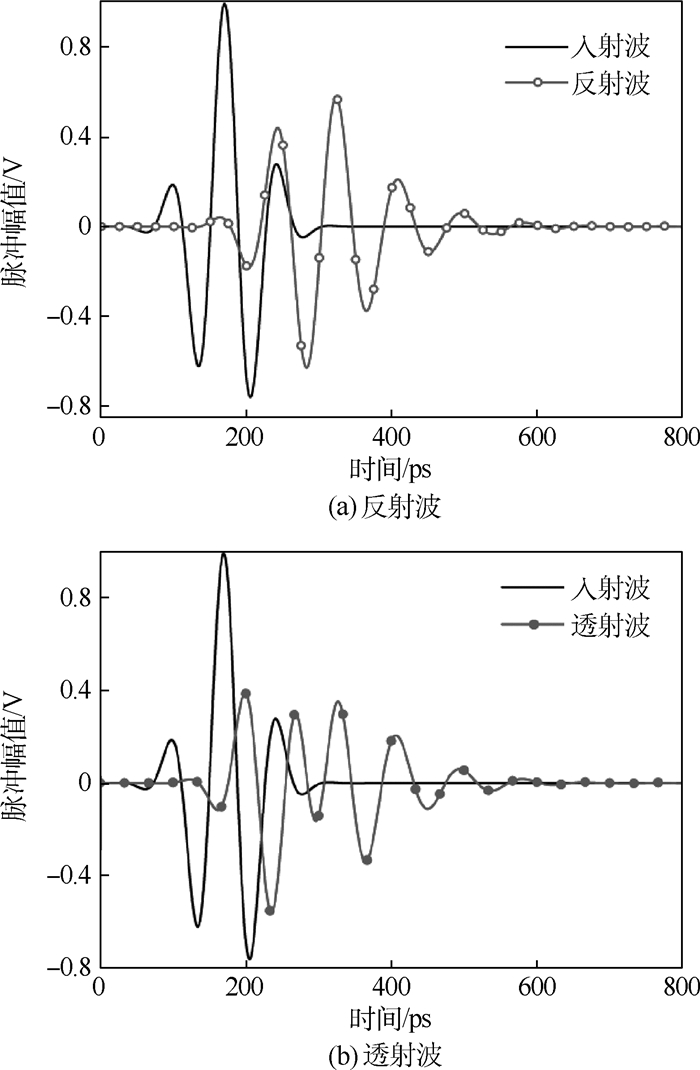
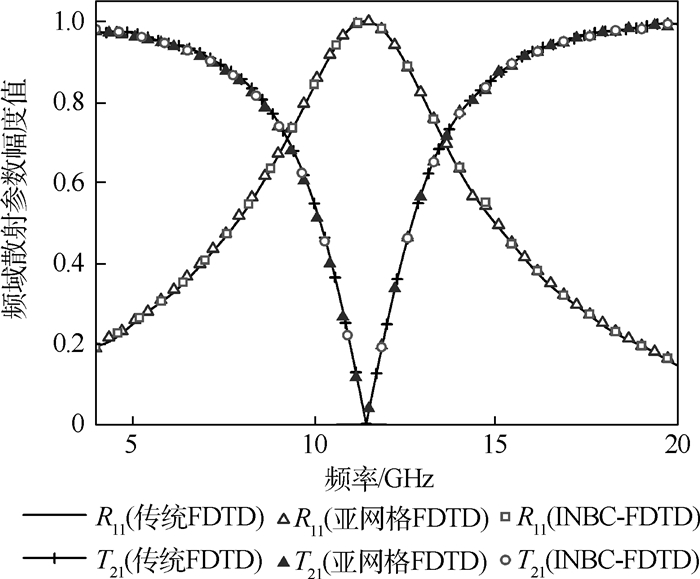
考虑如图 3所示的一个经典的十字贴片的频率选择表面(FSS)作为计算模型，激励入射波为中心频率12.27 GHz的双余弦调制高斯脉冲，其激励形式表达式见式(10)。用矢量拟合法对该结构的Y矩阵参数频域函数进行有理式拟合，对应的多项式参数在表 1和表 2中给出。采用一组网格参数Δx=Δy=Δz=0.25 mm(Δt=Δx (y, z)/(2c0))用于对FSS进行建模，并将其应用于INBC-FDTD方法中对结构的电磁特性参数进行数值计算。图 4(a)、(b)分别给出了入射波和透射波在时域的波形图；图 5给出了频域散射参数的幅度值。为了便于比较，将相同的网格参数应用于亚网格FDTD方法来对结构进行数值模拟。另外，选取一组尺寸为Δx=Δy=0.25 mm，Δz=10 μm的网格应用于传统FDTD方法，来对结构进行数值计算。这3种方法的具体计算参数在表 3中列出。可以看出，本文INBC-FDTD方法相对于其他2种方法来说具有较快的计算速度。
表 1 提取得到的十字贴片型FSS结构Y矩阵参数频域函数的等效有理式参数：极点pn及留数rnTable 1. Extracted values of poles (pn) and residues (rn) for Y-matrix coefficients of cross patched FSSn pn rn(Y11) rn(Y12/Y21) rn(Y22) 1 -7.637 7×106 1.582 5×109 -1.581 5×109 1.581 5×109 2 -3.572 0×1012 -1.812 0×1011 -2.284 1×1010 -4.030 7×1010 3, 4 -5.499 6×107±5.627 9×1010i 4.988 4×107±4.016 6×104i 1.510 7×105±8.706 3×103i -3.096 3×102±1.185 1×103i 5, 6 -5.759 2×108±5.660 8×1010i 1.463 5×107±5.061 7×104i 4.470 2×104±2.012 8×102i 1.468 2×102±1.464 3×103i 7, 8 -7.357 7×107±9.089 0×1010i 2.297 8×108±1.053 0×106i 6.637 8×105±3.934 0×104i 1.191 6×103±9.24×102i 表 2 提取得到的十字贴片型FSS结构Y矩阵参数频域函数的等效有理式参数：dTable 2. Extracted values of d for Y-matrix coefficients of cross patched FSSY d Y11 0.050 7 Y12 0.006 4 Y21 0.006 4 Y22 0.011 3 
图 4 十字贴片型FSS的反射波和透射波时域波形Figure 4. Reflected wave and transmitted wave of cross patched FSS in time domain
图 5 不同方法得出的频域散射参数幅度值Figure 5. Amplitude of scattering coefficients in frequency domain obtain by different methods表 3 不同方法的计算参数Table 3. Computational parameters for different methods方法 Δt 单元个数(长×宽×高) 时间步 CPU时间 传统FDTD 16.7 fs 41×41×1 040 60 000 18 d 亚网格FDTD 0.42 ps(粗网格)
16.7 fs(细网格)41×41×80 3 000 14 h INBC-FDTD 0.42 ps 41×41×80 3 000 17 min 3.2 方环形结构的互补型FSS
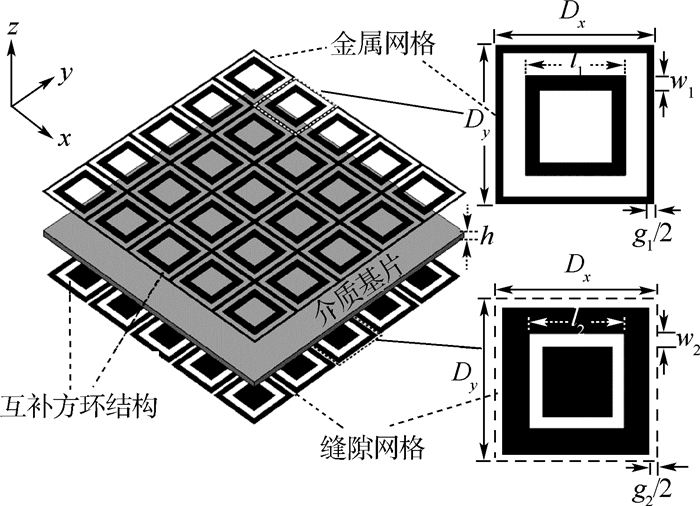
图 6为单元上下表面采用方环形结构的互补型FSS[15]。其上表面为方环形贴片，下表面为在接地面上开的尺寸相同的方环形缝隙，2个表面之间为厚度h=0.5 mm，相对介电常数εr=2.65的介质板。其结构参数为：单元周期Dx=Dy=D=8 mm，方形结构长度l1=l2=7 mm，宽度w1=w2=0.8 mm，方环之间的间距g1=g2=0.2 mm。
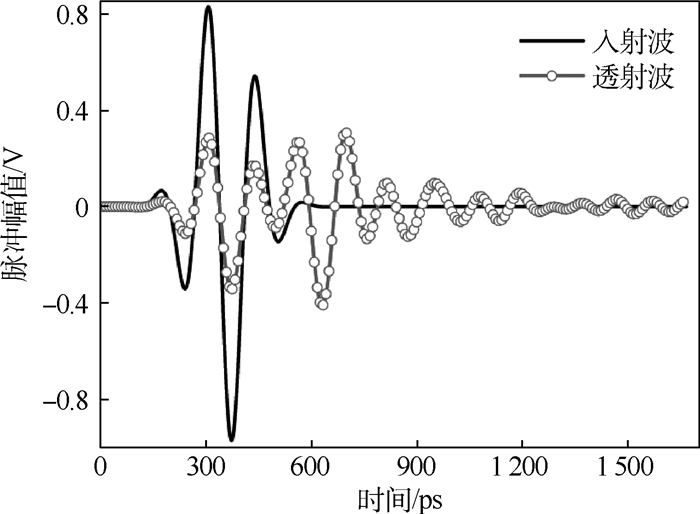
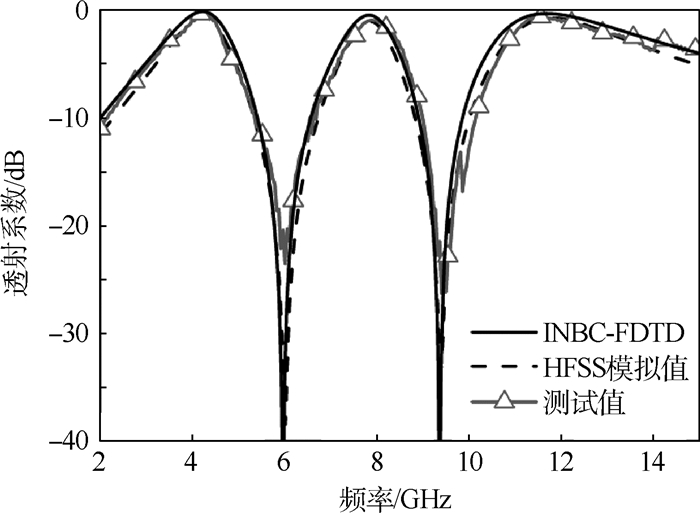
图 6 方环形结构的互补型FSS及其单元结构示意图Figure 6. Schematic diagram of complementary FSS with square ring and its unit cell对于如图 2所示的计算模型，将激励入射波设置为中心频率为8 GHz的双余弦调制高斯脉冲。用矢量拟合法对该结构的Y矩阵参数频域函数进行有理式拟合，对应的多项式参数在表 4和表 5中给出。使用Δx=Δy=Δz=0.25 mm(Δt=Δx(y, z)/(2c0))的网格用于对该FSS进行建模，并将其应用于INBC-FDTD方法中来对结构的电磁特性参数进行数值计算。图 7给出了透射波在时域的波形图；图 8给出了经INBC-FDTD方法计算得出的频域透射参数的幅度值。同样，为了便于比较，将相同的网格参数应用于亚网格FDTD方法来对结构进行数值模拟。这2种方法的具体计算参数在表 6中列出。可以看出，本文INBC-FDTD方法相对于亚网格FDTD方法来说具有比较快的计算速度。另外，在图 8中也给出了以上结构的透射系数(S21)测试数据。可以清楚地看到，各曲线吻合良好。
表 4 提取得到的方环形结构互补型FSS结构Y矩阵参数频域函数的等效有理式参数：极点pn及留数rnTable 4. Extracted values of poles (pn) and residues (rn) for Y-matrix coefficients of complementary FSS with square ringn pn rn(Y11) rn(Y12/Y21) rn(Y22) 1 -5.589 0×106 2.253 8×109 -1.846 6×109 1.757 6×109 2 -1.665 6×1012 -1.036 4×1011 -2.825 0×1010 -2.410 3×1011 3, 4 -1.991 8×108±3.937 3×1010i 4.629 1×106±1.976 9×105i -1.193 3×107±3.071 4×105i 3.011 3×107±3.314 0×105i 5, 6 -2.030 5×108±3.973 3×1010i 2.964 7×107±1.607 1×105i -7.124 1×107±3.997 4×105i 1.755 8×108±3.953 6×105i 7, 8 -3.195 7×108±6.586 5×1010i 4.565 9×108±3.611 6×106i -2.665 9×108±2.023 7×106i 1.555 8×108±1.25×106i 表 5 提取得到的方环形结构互补型FSS结构Y矩阵参数频域函数的等效有理式参数：dTable 5. Extracted values of d for the Y-matrix coefficients of complementary FSS with square ringY d Y11 0.062 4 Y12 0.016 9 Y21 0.016 9 Y22 0.144 6 
图 7 方环形结构互补型FSS的透射波时域波形Figure 7. Transmitted wave of complementary FSS with square ring in time domain
图 8 透射系数的频域波形比较Figure 8. Comparison of transmission coefficient waves in frequency domain表 6 两种方法计算参数的比较Table 6. Comparison of computational parameters for two methods方法 Δt 单元个数(长×宽×高) 时间步 CPU时间 亚网格
FDTD0.42 ps(粗网格)
16.7 fs(细网格)41×41×80 3 000 14 h INBC-FDTD 0.42 ps 41×41×80 3 000 17 min 4. 结论
本文提出了一种高效求解含有金属薄涂层周期结构时域电磁特性参数的INBC-FDTD方法。考虑到金属涂覆层的厚度很薄，如果使用尺寸统一的传统FDTD元胞对结构进行总体建模，对元胞的尺寸要求往往很苛刻，需要足够小来捕捉薄层中场的变化。
本文方法有以下优点：
1) 对整体结构采用粗网格建模，从而时间步将不再受金属层的厚度的限制。
2) 通过矢量拟合法拟合金属层的网络频域函数，从而可以避免复杂的频域至时域的卷积运算。
3) 精度高，计算速度快，可有效帮助工程师进行结构设计和优化分析。
-
图 1 系统结构模型向一体化设计模型的转化示意图
Figure 1. Schematic diagram of transformation from system structure model to integrated design model
图 3 节点N(1, 1)不同先验分布概率密度曲线
Figure 3. Probability density curves of different prior distribution at node N(1, 1)
表 1 一体化设计模型的CPT
Table 1. CPT of integrated design model
N(2, 1) 0 1 N(2, 2) 0 1 0 1 N(2, 3) 0 1 0 1 0 1 0 1 N(2, 4) 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 N(1, 1) 0 
1 
下载: 导出CSV
表 2 节点先验信息
Table 2. Prior information of each node
节点 继承先验超参数 专家信息融合 成败型数据 自先验超参数 a* b* 估计类型 转化形式 a b N(1, 1) 点估计型 
Beta分布
at=11.009
bt=0.945(10, 1) 20.009 1.945 N(2, 1) 点估计型 Beta分布
at=9.910
bt=0.944(20, 2) 27.910 2.944 N(2, 2) 点估计型 Beta分布
at=12.030
bt=0.947(24, 0) 36.030 0.947 N(2, 3) 31.2 3.6 区间估计型[0.861, 0.932] 成败型数据(211, 21) (28, 3) 246.2 27.6 N(2, 4) 点估计型 Beta分布
at=13.037
bt=0.951(30, 2) 41.037 2.951
下载: 导出CSV
表 3 二次电源系统FMECA信息
Table 3. FMECA information of secondary power system
节点 故障率λp/(10－6h-1) 故障模式M 故障模式频数比αj/% 故障模式影响概率βj 故障模式危害度Dji① 故障影响(扩散度)Ij② 被检测难度评分等级Ej② 标识码 模式名称 N(2, 1) 3.042 M1N(2, 1) 短路 20 1 4.259 4 2 M2N(2, 1) 退化 80 0.1 1.460 4 5 N(2, 2) 0.139 M1N(2, 2) 开路 92 1 0.384 3 2 M2N(2, 2) 参漂 8 0.5 0.017 3 4 N(2, 3) 10.516 M1N(2, 3) 退化 35 0.1 2.576 5 5 M2N(2, 3) 低温不启动 10 0.1 0.736 5 1 M3N(2, 3) 漏气 15 0.1 0.946 5 3 M4N(2, 3) 开路 15 1 11.042 5 2 M5N(2, 3) 短路 25 1 18.403 5 1 N(2, 4) 0.366 M1N(2, 4) 接触不良 80 0.8 1.640 1 2 M2N(2, 4) 开路 20 1 0.512 1 2 注：①指故障模式危害度, 通过文献[13]求解；②指本文以扩散度表征故障影响，可通过文献[27]求解。
下载: 导出CSV
表 4 不同样本分配方式结果对比
Table 4. Result comparison of different sample allocation methods
节点 故障模式M 基于故障率的样本分配[12] 基于危害度的样本分配[13] 基于故障属性的样本分配[27] 基于多因子的样本分配[15] 一体化设计方案 节点 故障模式 节点 故障模式 节点 故障模式 节点 故障模式 节点 故障模式 N(2, 1) M1N(2, 1) 10 2 6 4 8 4 1(2) 0(1) 6 3 M2N(2, 1) 8 2 4 1 3 N(2, 2) M1N(2, 2) 1(2) 1 0(2) 0(1) 1(2) 1 0(2) 0(1) 0(2) 0(1) M2N(2, 2) 0(1) 0(1) 0(1) 0(1) 0(1) N(2, 3) M1N(2, 3) 12 3 8 16 9 M2N(2, 3) 4 1 1 5 1 M3N(2, 3) 35 5 38 1 37 2 46 7 39 2 M4N(2, 3) 5 12 14 7 15 M5N(2, 3) 9 21 12 11 12 N(2, 4) M1N(2, 4) 1(2) 1 3 2 1(2) 1 0(2) 0(1) 2(3) 2 M2N(2, 4) 0(1) 1 0(1) 0(1) 0(1) 注：(·)内数字为基于式(29)校正后的样本量。
下载: 导出CSV
-
[1] 吴建军, 周红, 朱玉岭, 等.工程装备测试性分析与应用[M].北京:国防工业出版社, 2017.WU J J, ZHOU H, ZHU Y L, et al.Testability analysis and application of engineering equipment[M].Beijing:National Defense Industry Press, 2017(in Chinese). [2] 李华康.测试性试验中等效故障注入技术及应用[D].长沙: 国防科学技术大学, 2015.LI H K.Study on the equivalent fault injection technique and its application in testability test[D].Chagnsha: National University of Defense Technology, 2015(in Chinese). [3] 张西山, 黄考利, 敖贤野, 等.测试性验证试验中的故障样本综合加权分配方法[J].计算机测量与控制, 2015, 23(1):139-142. doi: 10.3969/j.issn.1671-4598.2015.01.043ZHANG X S, HUANG K L, AO X Y, et al.Synthetic weighted method of failure samples allocation in testability[J].Computer Measurement & Control, 2015, 23(1):139-142(in Chinese). doi: 10.3969/j.issn.1671-4598.2015.01.043 [4] 张艺琼, 刘萌萌, 李璠, 等.测试性验证试验方案的工程修正方法研究[J].测控技术, 2013, 32(2):126-127. doi: 10.3969/j.issn.1000-8829.2013.02.032ZHANG Y Q, LIU M M, LI F, et al.Study on engineering correction method of testability validation test plan[J].Measurement & Control Technology, 2013, 32(2):126-127(in Chinese). doi: 10.3969/j.issn.1000-8829.2013.02.032 [5] 张勇.装备测试性虚拟验证试验关键技术研究[D].长沙: 国防科学技术大学, 2012.ZHANG Y.Research on key technologies of virtual testability verification test for equipments[D].Chagnsha: National University of Defense Technology, 2012(in Chinese). [6] 常春贺, 杨江平, 曹鹏举.基于研制信息的测试性验证试验方案研究[J].航空学报, 2012, 33(11):2057-2064.CHANG C H, YANG J P, CAO P J.Study on the scheme of testability demonstration test based on development information[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(11):2057-2064(in Chinese). [7] 吴忠德, 邓露.基于验前试验信息熵的测试性验证试验方案[J].计算机测量与控制, 2016, 24(6):286-288.WU Z D, DENG L.Method for testability demonstration test design based on entropy of prior test information[J].Computer Measurement & Control, 2016, 24(6):286-288(in Chinese). [8] 李天梅, 邱静, 刘冠军.利用研制阶段试验数据制定测试性验证试验方案新方法[J].机械工程学报, 2009, 45(8):52-57.LI T M, QIU J, LIU G J.New methodology for determining testability integrated test scheme with test data in the development stages[J].Journal of Mechanical Engineering, 2009, 45(8):52-57(in Chinese). [9] WANG C, QIU J, LIU G, et al.Testability demonstration with component level data from virtual and physical tests[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014, 229(2):265-272. [10] 王敏, 杨江平, 卢雷, 等.利用分系统数据制定整机测试性验证试验方案[J].现代防御技术, 2015, 43(5):213-217. doi: 10.3969/j.issn.1009-086x.2015.05.034WANG M, YANG J P, LU L, et al.Determining testability demonstration test scheme with subsystem data[J].Modern Defence Technology, 2015, 43(5):213-217(in Chinese). doi: 10.3969/j.issn.1009-086x.2015.05.034 [11] 史贤俊, 王康, 韩旭, 等.基于层次Bayesian网络及后验风险准则的故障样本量确定方法[J].兵工学报, 2019, 40(1):171-181. doi: 10.3969/j.issn.1000-1093.2019.01.020SHI X J, WANG K, HAN X, et al.Method for determining fault sample size based on hierarchical Bayesian network and posterior risk criteria[J].Acta Armamentarii, 2019, 40(1):171-181(in Chinese). doi: 10.3969/j.issn.1000-1093.2019.01.020 [12] 李天梅, 邱静, 刘冠军.基于故障率的测试性验证试验故障样本分配方案[J].航空学报, 2009, 30(9):1661-1665. doi: 10.3321/j.issn:1000-6893.2009.09.017LI T M, QIU J, LIU G J.Allocation plan of failure samples based on failure rate in testability[J].Acta Aeronautica et Astronautica Sinca, 2009, 30(9):1661-1665(in Chinese). doi: 10.3321/j.issn:1000-6893.2009.09.017 [13] 赵建扬, 李小珉, 雷琴.基于危害度相对比值的故障样本分配方案[J].探测与控制学报, 2011, 33(2):55-59. doi: 10.3969/j.issn.1008-1194.2011.02.013ZHAO J Y, LI X M, LEI Q.Relative criticality ratio based on failure samples allocation[J].Journal of Detection & Control, 2011, 33(2):55-59(in Chinese). doi: 10.3969/j.issn.1008-1194.2011.02.013 [14] 余思奇, 景博, 黄以锋.基于贡献度的测试性验证试验样本分配方案研究[J].中国测试, 2015, 41(2):91-95. http://www.cnki.com.cn/Article/CJFDTotal-SYCS201502023.htmYU S Q, JING B, HUANG Y F.Study on allocation scheme of failure sample in testability validation tests based on contribution[J].China Measurment & Test, 2015, 41(2):91-95(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-SYCS201502023.htm [15] 何洋, 李洪涛, 王志新.基于多因子的机电设备测试性验证样本分配方案[J].电光与控制, 2015, 22(1):97-100. doi: 10.3969/j.issn.1671-637X.2015.01.022HE Y, LI H T, WANG Z X.A multi-factor based sample allocation scheme for testability verification of electromechanical equipment[J].Electronics Optics & Control, 2015, 22(1):97-100(in Chinese). doi: 10.3969/j.issn.1671-637X.2015.01.022 [16] 陈然, 连光耀, 黄考利, 等.基于FMECA信息的测试性验证试验样本分配方法[J].北京航空航天大学学报, 2017, 43(3):627-635. doi: 10.13700/j.bh.1001-5965.2016.0163CHEN R, LIAN G Y, HUANG K L, et al.Sample allocation method based on FMECA information for testability verification test[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3):627-635(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0163 [17] 刘磊.装备智能故障诊断及测试性验证与评价方法研究[D].郑州: 郑州大学, 2017.LIU L.Research on intelligent fault diagnosis and testability verification and evaluation methods of equipment[D].Zhengzhou: Zhengzhou University, 2017(in Chinese). [18] DURA-BERNAL S, WENNEKERS T, DENHAM S L.Modelling object perception in cortex: Hierarchical Bayesian networks and belief propagation[C]//2011 45th Annual Conference on Information Sciences and Systems.Piscataway, NJ: IEEE Press, 2011: 11990313. [19] 郑应荣.系统级层次化测试性建模与分析[D].哈尔滨: 哈尔滨工业大学, 2014.ZHENG Y R.Testability modeling and analysis of hierarchical system[D].Harbin: Harbin Institute of Technology, 2014(in Chinese). [20] WERHLI A V.Bayesian network structure inference with an hierarchical Bayesian model[C]//Advances in Artificial Intelligence-SBIA 2010.Berlin: Springer, 2010: 92-101. [21] 张西山, 黄考利, 闫鹏程, 等.基于不确定性测度与支持度的测试性验前信息融合方法[J].航空动力学报, 2015, 30(11):2779-2786.ZHANG X S, HUANG K L, YAN P C, et al.Testability prior information fusion method based on uncertainty measure and supporting degree[J].Journal of Aerospace Power, 2015, 30(11):2779-2786(in Chinese). [22] 王京, 李天梅, 何华锋, 等.多源测试性综合评估数据等效折合模型与方法研究[J].兵工学报, 2017, 38(1):151-159. doi: 10.3969/j.issn.1000-1093.2017.01.020WANG J, LI T M, HE H F, et al.Research on multi-source data equivalent methods for testablity integrated evaluation[J].Acta Armamentarii, 2017, 38(1):151-159(in Chinese). doi: 10.3969/j.issn.1000-1093.2017.01.020 [23] 邓琼.安全系统工程[M].西安:西北工业大学出版社, 2009.DENG Q.Safety system engineering[M].Xi'an:Northwestern Polytechnical University Press, 2009(in Chinese). [24] LITTLESTON N, WARMUTH M K.The weighted majority algorithm[J].Information and Computation, 1994, 108(2):212-261. doi: 10.1006/inco.1994.1009 [25] HART L.Reliability of modified designs:A Bayes analysis of an accelerated test of electronic assemblies[J].IEEE Transactions on Reliability, 1990, 39(2):140-144. doi: 10.1109/24.55871 [26] 张西山, 黄考利, 闫鹏程, 等.基于验前信息的测试性验证试验方案确定方法[J].北京航空航天大学学报, 2015, 41(8):1505-1512. doi: 10.13700/j.bh.1001-5965.2014.0628ZHANG X S, HUANG K L, YAN P C, et al.Method of confirming testability verification test scheme based on prior information[J].Journal of Beijing University of Aeronautics and Astronantics, 2015, 41(8):1505-1512(in Chinese). doi: 10.13700/j.bh.1001-5965.2014.0628 [27] 邓露, 许爱强, 赵秀丽.基于故障属性的测试性验证试验样本分配方案[J].测试技术学报, 2014, 28(2):103-107.DENG L, XU A Q, ZHAO X L.Allocation plan for samples based on failure attribute in testability demonstration test[J].Journal of Test and Measurement Technology, 2014, 28(2):103-107(in Chinese). 期刊类型引用(0)
其他类型引用(2)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 880
- HTML全文浏览量: 112
- PDF下载量: 222
- 被引次数: 2
