基于导重法的自重载荷下悬臂梁结构拓扑优化

任毅如; 向剑辉; 何杰; 宁克焱; 杨玲玲

doi:10.13700/j.bh.1001-5965.2020.0191

基于导重法的自重载荷下悬臂梁结构拓扑优化

doi: 10.13700/j.bh.1001-5965.2020.0191

1.
湖南大学机械与运载工程学院, 长沙 410082
2.
中国北方车辆研究所, 北京 100072

基金项目:

工业和信息化部基础产品创新科研项目 237099000000170008

详细信息

通讯作者:
任毅如. E-mail: renyiru@hnu.edu.cn

中图分类号: TP314;TH111;O343
计量
- 文章访问数: 742
- HTML全文浏览量: 91
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-18
- 录用日期: 2020-06-05
- 网络出版日期: 2021-07-20

Topology optimization of cantilever structure with self-weight load based on guide-weight method

1.
College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China
2.
China North Vehicle Research Institute, Beijing 100072, China

Funds:

Innovation Research Project of Basic Product of Ministry of Industry and Information Technology of China 237099000000170008

More Information

Corresponding author: REN Yiru. E-mail: renyiru@hnu.edu.cn

摘要

摘要:
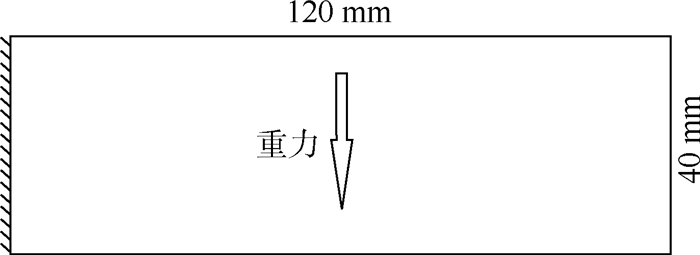
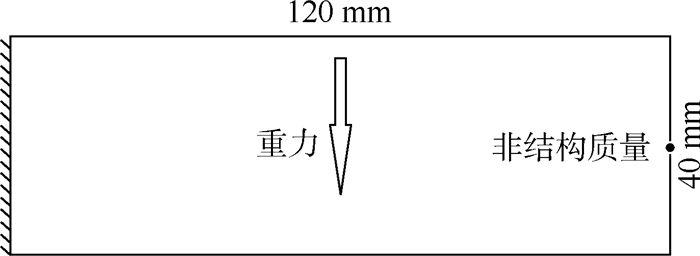
针对自重载荷悬臂梁结构拓扑优化末端区域材料分布不收敛的问题，提出了一种拓扑优化方法。根据虚功相等原理，利用四节点矩形单元的形函数、单元体积密度和质量的关系建立了载荷等效方法。根据优化模型的Kuhn-Tucker条件推导出了导重准则，以及目标函数的灵敏度公式和考虑自重载荷拓扑优化的迭代算法。针对自重载荷作用下悬臂梁结构拓扑优化存在的末端区域材料分布模糊问题，研究了变密度法和非结构质量相结合的求解策略，揭示了典型因素对拓扑结构的影响规律。结果表明：所提方法能够解决自重载荷下悬臂梁末端区域材料分布模糊问题。
- 拓扑优化 /
- 导重法 /
- 变密度法 /
- 自重载荷 /
- 材料属性有理近似函数插值(RAMP)模型
Abstract:
Aiming at the problem of non-convergence of the material distribution at the end of the cantilever beam structure under self-weight load, a topology optimization method for the cantilever beam structure under self-weight load is proposed to solve the problem. According to the principle of virtual work equal, the load equivalent method was established by the relationship among the shape function of the four-node rectangular element, the unit volume density and the mass. According to the Kuhn-Tucker condition of the optimization model, the guide-weight criterion was derived, the sensitivity formula of the objective function was obtained, and the iterative formula considering the topology optimization of the self-weight load was derived. Aimed at the problem of ambiguity of material distribution in the end region of the topological optimization of a cantilever beam structure under self-weight load, a solution strategy combining variable density method and non-structural mass was studied, and the influence of typical factors on the topological structure was revealed. The results show that this method can solve the problem of fuzzy material distribution at the end of a cantilever beam under self-weight.
- topology optimization /
- guide-weight method /
- variable density method /
- self-weight load /
- Rational Approximation of Material Properties (RAMP) model

HTML全文

图 1 自重载荷作用下的二维简支梁受力结构

Figure 1. Structural diagram of 2D simply supported beam under self-weight load

下载: 全尺寸图片幻灯片

图 2 待优化结构的有限元模型

Figure 2. Finite element model of structure to be optimized

下载: 全尺寸图片幻灯片

图 3 二维简支梁结构拓扑优化过程

Figure 3. Topology optimization process of 2D simply supported beam structure

下载: 全尺寸图片幻灯片

图 4 二维简支梁拓扑优化结果应力分析

Figure 4. Stress analysis of 2D simply supported beam topology optimization results

下载: 全尺寸图片幻灯片

图 5 优化前二维简支梁结构应力分析

Figure 5. Stress analysis of 2D simply supported beam structure before optimization

下载: 全尺寸图片幻灯片

图 6 自重载荷作用下结构应力分析

Figure 6. Structural stress analysis under self-weight load

下载: 全尺寸图片幻灯片

图 7 自重载荷作用下的二维悬臂梁结构示意图

Figure 7. Schematic diagram of 2D cantilever beam under self-weight load

下载: 全尺寸图片幻灯片

图 8 自重载荷作用下的二维悬臂梁拓扑优化结果

Figure 8. Topology optimization results of 2D cantileverbeam under self-weight load

下载: 全尺寸图片幻灯片

图 9 不同长高比下的悬臂梁拓扑优化结果

Figure 9. Topology optimization results of cantilever beams with different aspect ratios

下载: 全尺寸图片幻灯片

图 10 施加非结构质量的悬臂梁结构示意图

Figure 10. Schematic diagram of a cantilever beam with non-structural mass

下载: 全尺寸图片幻灯片

图 11 不同非结构质量情况下悬臂梁的拓扑优化结果

Figure 11. Topology optimization results of cantilever beams with different non-structural masses

下载: 全尺寸图片幻灯片

图 12 r=1悬臂梁拓扑优化结果应力分析

Figure 12. Stress analysis of r=1 cantilever beam topology optimization results

下载: 全尺寸图片幻灯片

图 13 r=0.1悬臂梁拓扑优化结果应力分析

Figure 13. Stress analysis of r=0.1 cantilever beam topology optimization results

下载: 全尺寸图片幻灯片

图 14 r=0.04悬臂梁拓扑优化结果应力分析

Figure 14. Stress analysis of r=0.04 cantilever beam topology optimization results

下载: 全尺寸图片幻灯片

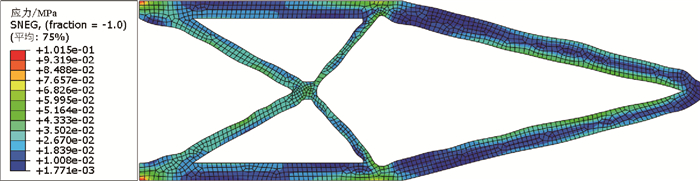
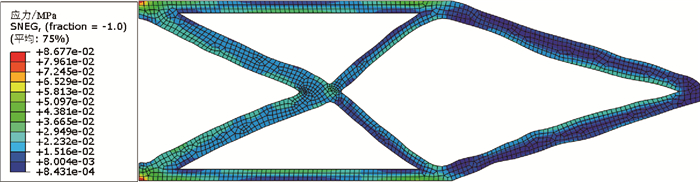
表 1 悬臂梁结构自重载荷下应力峰值

Table 1. Peak stress of cantilever beam structure under self-weight load

非结构质量比值	峰值应力/MPa
1	10.15×10^-2
0.1	8.677×10^-2
0.04	6.219×10^-2

下载: 导出CSV

参考文献(23)

[1]	赵军鹏, 王春洁. 载荷不确定条件下的结构拓扑优化算法[J]. 北京航空航天大学学报, 2014, 40(7): 959-964. doi: 10.13700/j.bh.1001-5965.2013.0476 ZHAO J P, WANG C J. Algorithm of structural topology optimization under loading uncertainty[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 959-964(in Chinese). doi: 10.13700/j.bh.1001-5965.2013.0476
[2]	付志方, 王春洁. 载荷不确定的周期性结构稳健拓扑优化[J]. 北京航空航天大学学报, 2017, 43(4): 747-753. doi: 10.13700/j.bh.1001-5965.2016.0822 FU Z F, WANG C J. Robust topology optimization of periodic structures under uncertain loading[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 747-753(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0822
[3]	贾娇, 程伟, 龙凯. 基于SIMP法的周期性传热材料拓扑优化[J]. 北京航空航天大学学报, 2015, 41(6): 1042-1048. doi: 10.13700/j.bh.1001-5965.2014.0401 JIA J, CHENG W, LONG K. Topology optimization for periodic thermal conductive material using SIMP method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1042-1048(in Chinese). doi: 10.13700/j.bh.1001-5965.2014.0401
[4]	李明高, 李明, 韩璐, 等. 基于多目标的高速列车隔热结构拓扑优化[J]. 北京航空航天大学学报, 2016, 42(5): 878-884. doi: 10.13700/j.bh.1001-5965.2015.0539 LI M G, LI M, HAN L, et al. Multi-objective topological optimization of heat insulation structures used in high-speed train[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(5): 878-884(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0539
[5]	郭连水, BANDI P, RENAUD J E. 一种大变形多空间域连续体结构拓扑优化方法[J]. 北京航空航天大学学报, 2009, 35(2): 227-230. https://bhxb.buaa.edu.cn/CN/abstract/abstract9035.shtml GUO L S, BANDI P, RENAUD J E. Method of multi-domain topology optimization for continuum structures[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 227-230(in Chinese). https://bhxb.buaa.edu.cn/CN/abstract/abstract9035.shtml
[6]	刘丰睿, 赵丽滨, 韩邦成, 等. 磁悬浮控制力矩陀螺框架结构的拓扑优化设计[J]. 北京航空航天大学学报, 2010, 36(4): 455-458. https://bhxb.buaa.edu.cn/CN/abstract/abstract8479.shtml LIU F R, ZHAO L B, HAN B C, et al. Topology optimization design of frame structure for magnetic suspension control moment gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4): 455-458(in Chinese). https://bhxb.buaa.edu.cn/CN/abstract/abstract8479.shtml
[7]	陶扬, 王春洁, 付志方. 卫星天线复合材料框架的铺层优化设计[J]. 北京航空航天大学学报, 2017, 43(5): 1031-1037. doi: 10.13700/j.bh.1001-5965.2016.0392 TAO Y, WANG C J, FU Z F. Layup design optimization of composite frame for satellite antenna[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(5): 1031-1037(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0392
[8]	陈树勋, 叶尚辉. 天线结构优化设计的准则法[J]. 固体力学学报, 1984(4): 482-497. https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX198404001.htm CHEN S X, YE S H. Guide-weight method for structural topology optimization[J]. Chinese Journal of Computational Mechanics, 1984(4): 482-497(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX198404001.htm
[9]	BENDSOE M P. Optimal shape design as a material distribution problem[J]. Structural Optimization, 1989, 1(4): 193-202. doi: 10.1007/BF01650949
[10]	PEDERSEN N L. Maximization of eigenvalues using topology optimization[J]. Structural and Multidisciplinary Optimization, 2000, 20(1): 2-11. doi: 10.1007/s001580050130
[11]	STOLPE M, SVANBERG K. An alternative interpolation scheme for minimum compliance topology optimization[J]. Structural and Multidisciplinary Optimization, 2001, 22(2): 116-124. doi: 10.1007/s001580100129
[12]	BRUYNEEL M, DUYSINX P. Note on topology optimization of continuum structures including self-weight[J]. Structural and Multidisciplinary Optimization, 2005, 29(4): 245-256. doi: 10.1007/s00158-004-0484-y
[13]	LOPES R A, STUMP F V, SILVA E C N. Topology optimization of three dimensional structures under self-weight and inertial forces[C]//6th World Congress of Structural and Multidisciplinary Optimization, 2005: 5-6.
[14]	LIU X J, LI Z D, WANG L P, et al. Solving topology optimization problems by the guide-weight method[J]. Frontiers of Mechanical Engineering, 2011, 6(1): 136-150. http://www.cnki.com.cn/Article/CJFDTotal-JEXG201106023.htm
[15]	LIU X J, LI Z D, CHEN X. A new solution for topology optimization problems with multiple loads: The guide-weight method[J]. Science China Technological Sciences, 2011, 54(6): 1505. doi: 10.1007/s11431-011-4334-z
[16]	陈祥, 刘辛军. 基于RAMP插值模型结合导重法求解拓扑优化问题[J]. 机械工程学报, 2012, 48(1): 135-140. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201201021.htm CHEN X, LIU X J. Solving topology optimization problems based on RAMP method combined with guide-weight method[J]. Journal of Mechanical Engineering, 2012, 48(1): 135-140(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201201021.htm
[17]	张晖, 刘书田, 张雄. 考虑自重载荷作用的连续体结构拓扑优化[J]. 力学学报, 2009, 41(1): 98-104. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200901016.htm ZHANG H, LIU S T, ZHANG X. Topology optimization of continuum structures subjected to self weight loads[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 98-104(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200901016.htm
[18]	XU H Y, GUAN L W, CHEN X, et al. Guide-weight method for topology optimization of continuum structures including body forces[J]. Finite Elements in Analysis and Design, 2013, 75: 38-49. doi: 10.1016/j.finel.2013.07.002
[19]	许华旸, 关立文, 王立平, 等. 惯性载荷下飞行模拟器大臂结构的拓扑优化[J]. 机械工程学报, 2014, 50(9): 14-23. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201409002.htm XU H Y, GUAN L W, WANG L P, et al. Topology optimization for the arm of flight simulator under inertial loads[J]. Journal of Mechanical Engineering, 2014, 50(9): 14-23(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201409002.htm
[20]	JAIN N, SAXENA R. Effect of self-weight on topological optimization of static loading structures[J]. Alexandria Engineering Journal, 2018, 57(2): 527-535. doi: 10.1016/j.aej.2017.01.006
[21]	HOLMBERG E, THORE C J, KLARBRING A. Worst-case topology optimization of self-weight loaded structures using semi-definite programming[J]. Structural and Multidisciplinary Optimization, 2015, 52(5): 915-928. doi: 10.1007/s00158-015-1285-1
[22]	陈树勋. 精密复杂结构的几种现代设计方法[M]. 北京: 北京航空航天大学出版社, 1992: 226-244. CHEN X S. Several modern design methods for precise and complex structures[M]. Beijing: Beihang University Press, 1992: 226-244(in Chinese).
[23]	陈树勋. 工程结构系统的分析, 综合与优化设计[M]. 北京: 中国科学文化出版社, 2008: 99-108. CHEN S X. Analysis, synthesis and optimization of engineering structural system[M]. Beijing: China Science Culture Publishing House, 2008: 99-108(in Chinese).