-
摘要:
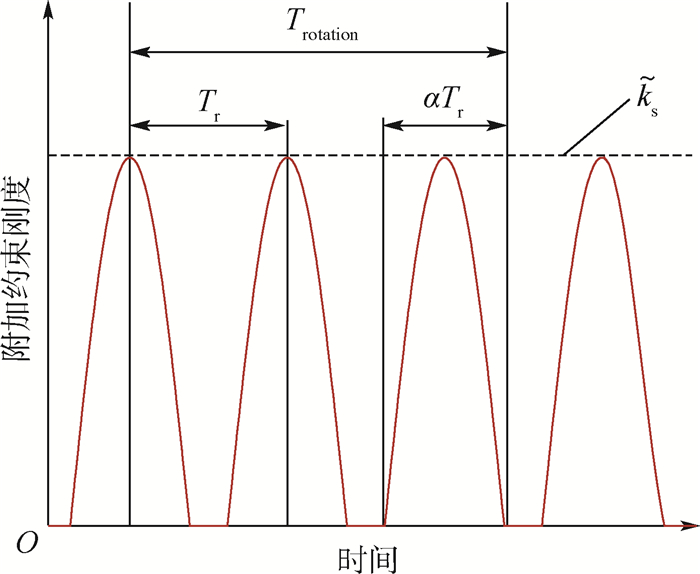
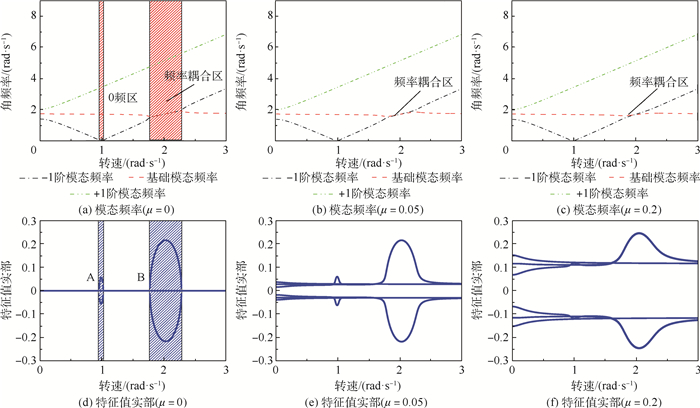
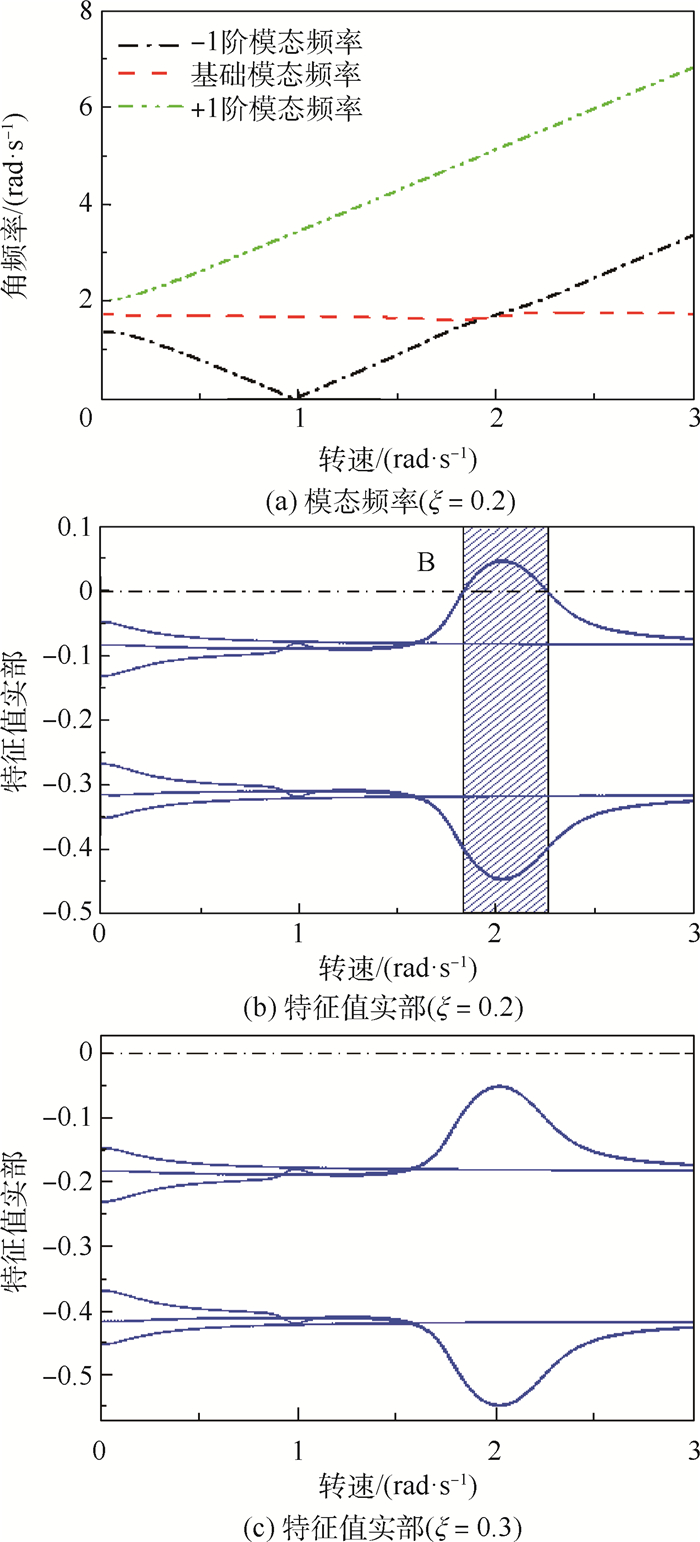
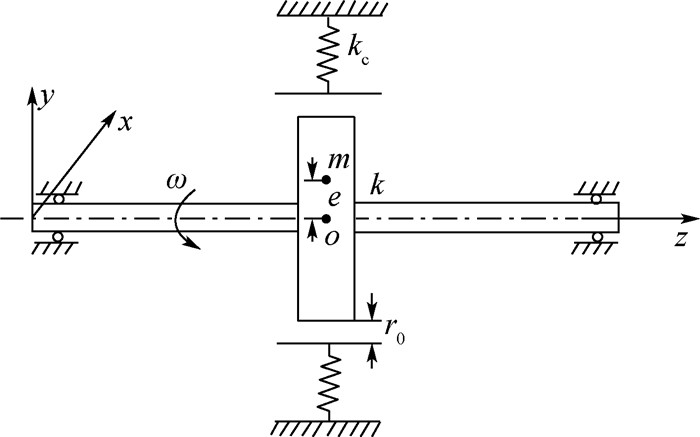
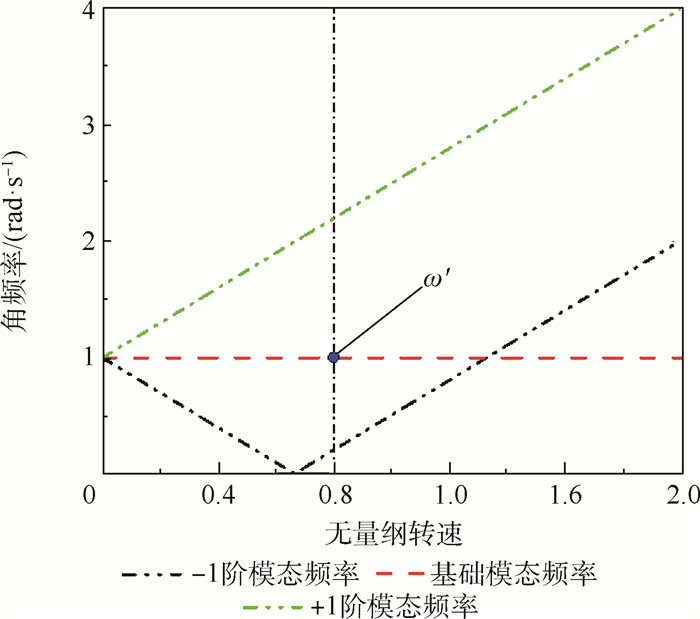
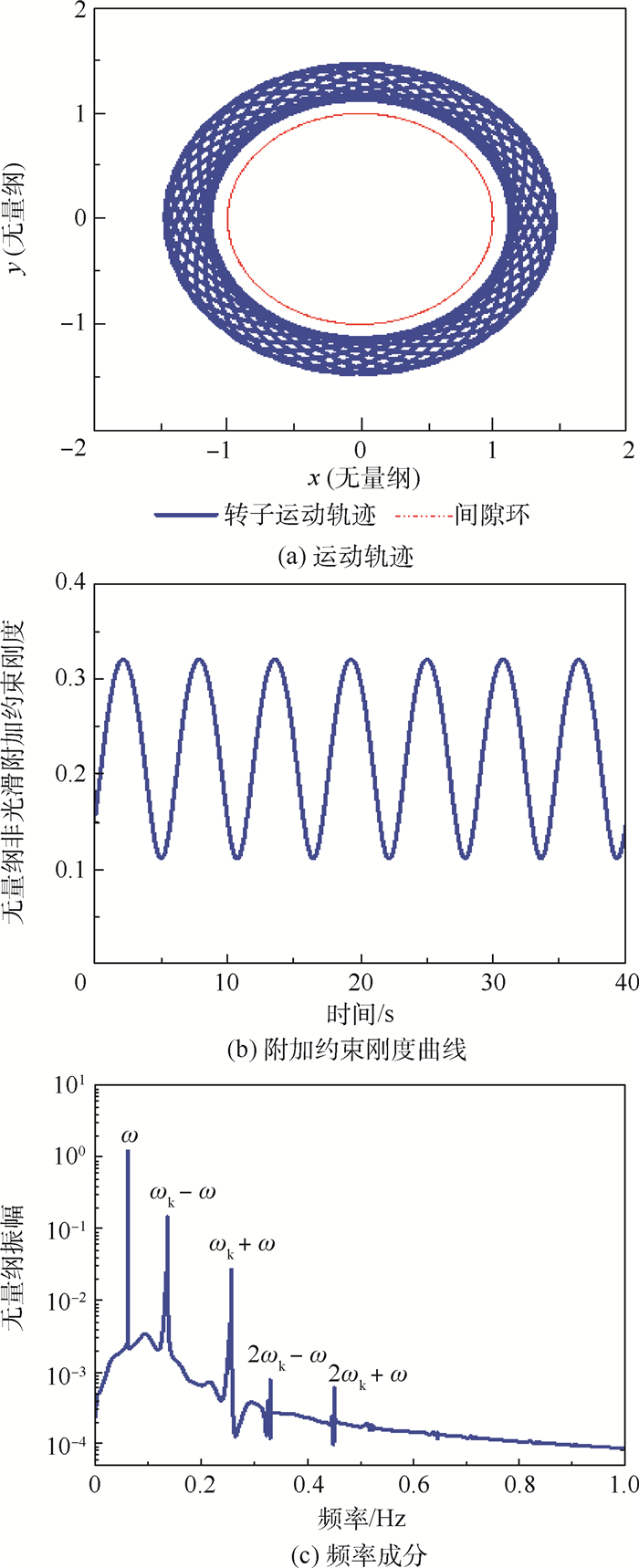
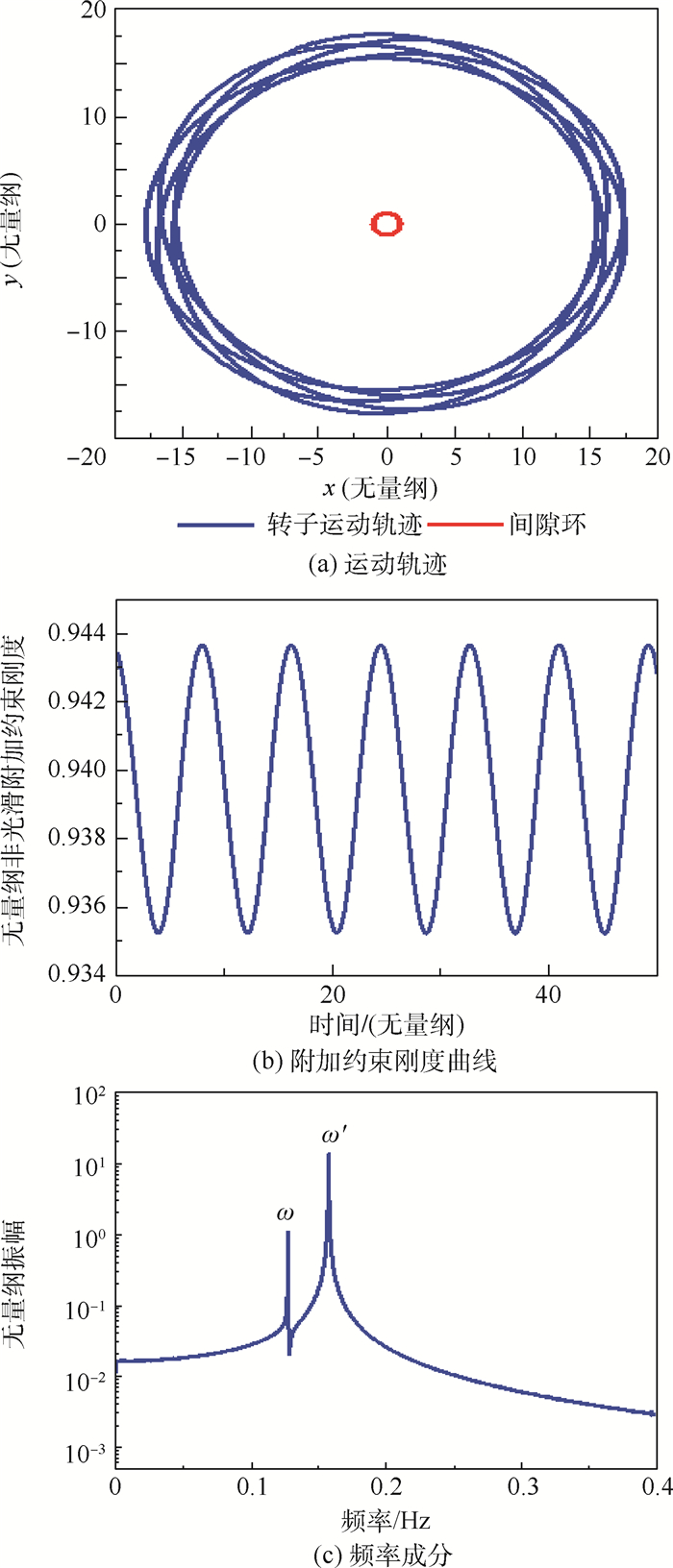
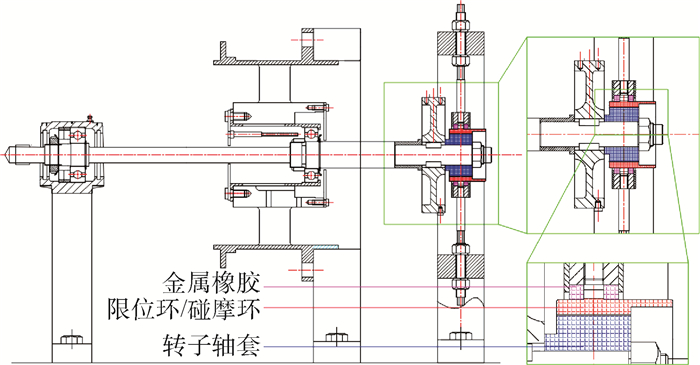
光滑时变约束是转静子碰摩所产生的一种力学效果，指静子与转子发生持续接触，静子对转子产生周期时变的约束作用，转子在该约束下的附加刚度曲线是一条光滑可导的函数。根据试验转子在光滑时变约束下的附加刚度曲线建立一种光滑时变约束模型，基于Hill行列式理论分析光滑时变约束转子的模态频率、稳定性及响应，为碰摩转子故障识别和稳定性分析提供一种分析途径。结果表明：光滑时变约束下转子具有频率耦合、多频、失稳特性。失稳转速区中，转子的幅值随时间逐渐增大，引起转子失稳的频率成分即为转子模态分析中特征值实部大于0的频率成分；非失稳转速区中，转子的频率成分主要为转速频率和波动频率构成的频率组合。
Abstract:The smooth time-varying constraint is a mechanical effect of continuous contact produced by the rubbing between rotor and stator, in which the periodic time-varying constraint is applied to the rotor. The additional stiffness curve caused by contact between the stator and the rotor is a smooth and derivable function with time. A smooth time-varying constraint model is established based on the orbit of rotor in experiment, and the modal frequency, stability and response of rotor system with smooth time-varying constraint are analyzed based on the Hill method, which provides an analysis frame for the fault identification and stability analysis of the rubbing rotor. The research results show that the rotor with smooth time-varying constraint has the characteristics of frequency coupling, multi-frequency and instability. In the unstable speed region, the amplitude of the rotor gradually increases with time. The frequency component that causes the instability of the rotor system is the frequency component whose real part of eigenvalue is greater than 0 in the rotor modal analysis. In the stable speed region, the rotor's frequency response is mainly the frequency combination composed of speed frequency and contact frequency.
-
Key words:
- smooth time-varying /
- rotor /
- modal characteristics /
- stability /
- response
-
图 3 不同机匣刚度下约束刚度随时间变化
Figure 3. Constraint stiffness changing with time with different case stiffness
图 8 波动刚度比对模态特性的影响
Figure 8. Influence of wave stiffness ratio on modal characteristics
图 10 平均刚度比对模态特性的影响
Figure 10. Influence of average stiffness ratio on modal characteristics
图 16 经典Jeffcott转子碰摩模型响应特性
Figure 16. Response characteristics of classic Jeffcott rubbing rotor model
图 17 光滑时变约束转子系统模态频率
Figure 17. Modal frequency of smooth time-varying constrained rotor system
图 18 经典Jeffcott转子系统ω=0.38转速响应特性
Figure 18. Response characteristics of classic Jeffcott rubbing rotor model with rotational speed ω=0.38
-
[1] CHU F, LU W. Stiffening effect of the rotor during the rotor-to-stator rub in a rotating machine[J]. Journal of Sound and Vibration, 2007, 308(3): 758-766. http://www.onacademic.com/detail/journal_1000034094284710_78a3.html [2] TAI X, MA H, LIU F, et al. Stability and steady-state response analysis of a single rub-impact rotor system[J]. Archive of Applied Mechanics, 2015, 85(1): 133-148. doi: 10.1007/s00419-014-0906-2 [3] EHRICH, FREDRIC F. Observations of nonlinear phenomena in rotordynamics[J]. Journal of System Design & Dynamics, 2008, 2(3): 641-651. http://www.onacademic.com/detail/journal_1000039717379710_d720.html [4] EHRICH F. Observations of subcritical superharmonic and chaotic response in rotordynamics[J]. Journal of Vibration and Acoustics, 1992, 114(1): 93-100. doi: 10.1115/1.2930240 [5] GONSALVES D H, NEILSON R D, BARR A D S. A study of the response of a discontinuously nonlinear rotor system[J]. Nonlinear Dynamics, 1995, 7(4): 451-470. doi: 10.1007/BF00121108 [6] BLACK H F. Interaction of a whirling rotor with a vibrating stator across a clearance annulus[J]. Journal of Mechanical Engineering Science, 1968, 10(1): 1-12. doi: 10.1243/JMES_JOUR_1968_010_003_02 [7] 张华彪, 陈予恕. 非线性转子的反向全周碰摩响应[J]. 振动与冲击, 2013, 32(10): 84-90. doi: 10.3969/j.issn.1000-3835.2013.10.016ZHANG H B, CHEN Y S. Reverse full annular rub of a nonlinear rotor system[J]. Journal of Vibration and Shock, 2013, 32(10): 84-90(in Chinese). doi: 10.3969/j.issn.1000-3835.2013.10.016 [8] JIANG J, ULBRICH H. The physical reason and the analytical condition for the onset of dry whip in rotor-to-stator contact systems[J]. Journal of Vibration and Acoustics, 2005, 127(6): 594-603. doi: 10.1115/1.1888592 [9] MUSZYNSKA A. Rotor-to-stationary element rub-related vibration phenomena in rotating machinery-Literature suryey[J]. The Shock and Vibration Digest, 1989, 21(3): 3-11. doi: 10.1177/058310248902100303 [10] CHOI Y S. Dynamics of rotor rub in annular clearance with experimental evaluation[J]. Journal of Mechanical Science and Technology, 1994, 8(4): 404-413. http://www.onacademic.com/detail/journal_1000034415908310_e760.html [11] ZILLI A, WILLIAMS R J, EWINS D J. Nonlinear dynamics of a simplified model of an overhung rotor subjected to intermittent annular rubs[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(6): 065001. doi: 10.1115/1.4028844 [12] SINHA S K. Non-linear dynamic response of a rotating radial Timoshenko beam with periodic pulse loading at the free-end[J]. International Journal of Non-Linear Mechanics, 2005, 40(1): 113-149. doi: 10.1016/j.ijnonlinmec.2004.05.019 [13] DAI X, ZHANG X, JIN X. The partial and full rubbing of a flywheel rotor-bearing-stop system[J]. International Journal of Mechanical Sciences, 2001, 43(2): 505-519. doi: 10.1016/S0020-7403(99)00121-6 [14] WANG C, ZHANG D, MA Y, et al. Theoretical and experimental investigation on the sudden unbalance and rub-impact in rotor system caused by blade off[J]. Mechanical Systems and Signal Processing, 2016, 76: 111-135. http://smartsearch.nstl.gov.cn/paper_detail.html?id=213bf01925e5c0f980cb248bac6d409e [15] ABUZAID M A, ELESHAKY M E, ZEDAN M G. Effect of partial rotor-to-stator rub on shaft vibration[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 170-182. doi: 10.1007/s12206-008-0717-x [16] GOLDMAN P, MUSZYNSKA A. Chaotic behavior of rotor/stator systems with rubs[J]. Journal of Engineering for Gas Turbines and Power, 1994, 116(3): 692-701. doi: 10.1115/1.2906875 [17] HONG J, PINGCHAO Y U, ZHANG D, et al. Modal characteristics analysis for a flexible rotor with non-smooth constraint due to intermittent rub-impact[J]. Chinese Journal of Aeronautics, 2018, 31(3): 498-513. doi: 10.1016/j.cja.2018.01.003 [18] JIANG J. The analytical solution and the existence condition of dry friction backward whirl in rotor-to-stator contact systems[J]. Journal of Vibration and Acoustics, 2007, 129(2): 260-264. doi: 10.1115/1.2345677 -
下载:
点击查看大图
计量
- 文章访问数: 319
- HTML全文浏览量: 77
- PDF下载量: 235
- 被引次数: 0
