基于学习的中段反导拦截时间和拦截点预测方法

杨子成; 鲜勇; 李少朋; 任乐亮; 张大巧

doi:10.13700/j.bh.1001-5965.2020.0409

基于学习的中段反导拦截时间和拦截点预测方法

doi: 10.13700/j.bh.1001-5965.2020.0409

火箭军工程大学作战保障学院, 西安 710025

详细信息

通讯作者:
鲜勇, E-mail: xy603xy@163.com

中图分类号: V412.4;TJ761.3
计量
- 文章访问数: 410
- HTML全文浏览量: 109
- PDF下载量: 83
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-09
- 录用日期: 2020-10-27
- 网络出版日期: 2021-11-20

Prediction method of intercept time and intercept point based on learning mid-course antimissile

College of War Support, Rocket Force Engineering University, Xi'an 710025, China

More Information

Corresponding author: XIAN Yong, E-mail: xy603xy@163.com

摘要

摘要:
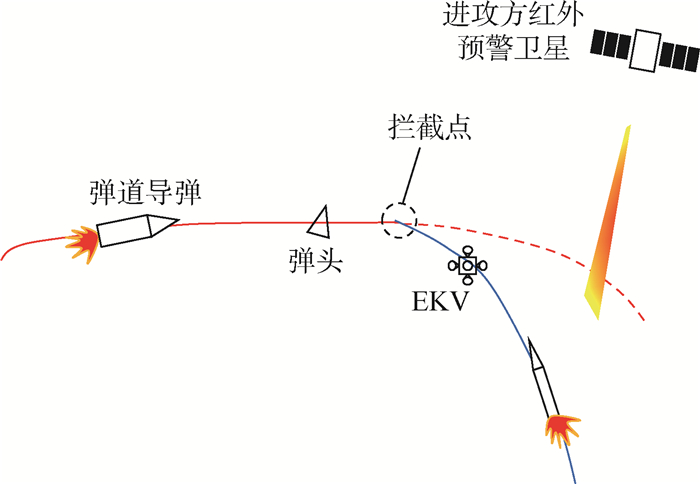
弹道导弹实时、准确地预测拦截弹的拦截点与拦截时间，是实现中段突防的有效手段。针对弹道导弹中段突防中的拦截点坐标及拦截时间的预测问题，提出了一种基于监督学习的在线预测方法。以拦截弹的主动段关机参数和关机时刻为输入量，建立拦截时间和拦截点预测模型。在多层感知机神经网络的基础上构建有监督学习算法，通过攻防仿真获取拦截弹的参数制作训练数据集，在线下完成网络训练。仿真结果表明：神经网络能够有效在线预测拦截时间和拦截点坐标，预测结果的相对误差分别为0.124 3%和0.128 5%，拦截时间预测结果误差的平均值为0.224 0 s，拦截点预测结果距离误差平均值为2 016.48 m，均满足精度要求。
- 中段突防 /
- 拦截点预测 /
- 拦截时间预测 /
- 监督学习 /
- 神经网络
Abstract:
Accurately predicting the intercept point and intercept time of the interceptor in real time is an effective way to realize the mid-course penetration of ballistic missiles. In order to predict the intercept point coordinates and intercept time during the mid-course penetration process of ballistic missile, an online prediction method based on supervised learning is proposed in this paper. Using the shutdown parameters and the shutdown time of the boost stage of the interceptor as inputs, the prediction model of intercept time and intercept point was established. Based on the multi-layer perceptron neural network, a supervised learning algorithm was formulated, and the interceptor's parameters were obtained through the attack and defense simulation to make the set of training data. The network training was completed offline. The simulation results show that the neural network can effectively predict the interception time and the coordinates of interception point online, and the relative error of the prediction results is 0.124 3% and 0.128 5% respectively; the average error of the prediction results of intercept time is 0.224 0 s; the average distance error of the prediction results of intercept point is 2 016.48 m. They all meet the accuracy requirements.
- mid-course penetration /
- intercept point prediction /
- intercept time prediction /
- supervised learning /
- neural network

HTML全文

图 1 中段拦截对抗示意图

Figure 1. Schematic diagram of midcourse interception and confrontation

下载: 全尺寸图片幻灯片

图 2 拦截时间预测模型示意图

Figure 2. Schematic diagram of intercept time prediction model

下载: 全尺寸图片幻灯片

图 3 拦截点预测模型示意图

Figure 3. Schematic diagram of intercept point prediction model

下载: 全尺寸图片幻灯片

图 4 拦截时间预测网络结构

Figure 4. Intercept time prediction network structure

下载: 全尺寸图片幻灯片

图 5 拦截点预测网络结构

Figure 5. Intercept point prediction network structure

下载: 全尺寸图片幻灯片

图 6 拦截时间与拦截点预测流程

Figure 6. Flowchart of prediction of intercept time and intercept point

下载: 全尺寸图片幻灯片

图 7 拦截时间预测网络训练过程

Figure 7. Intercept time prediction network training process

下载: 全尺寸图片幻灯片

图 8 拦截点预测网络训练过程

Figure 8. Intercept point prediction network training process

下载: 全尺寸图片幻灯片

图 9 拦截时间预测误差统计直方图

Figure 9. Histogram of intercept time prediction error

下载: 全尺寸图片幻灯片

图 10 拦截时间部分样本预测误差

Figure 10. Intercept time partial sample prediction error

下载: 全尺寸图片幻灯片

图 11 拦截时间预测误差箱型图

Figure 11. Error box plot of intercept time prediction

下载: 全尺寸图片幻灯片

图 12 X轴方向拦截点坐标预测误差统计直方图

Figure 12. Histogram of X-axis intercept point's coordinate prediction error

下载: 全尺寸图片幻灯片

图 13 Y轴方向拦截点坐标预测误差统计直方图

Figure 13. Histogram of Y-axis intercept point's coordinate prediction error

下载: 全尺寸图片幻灯片

图 14 Z轴方向拦截点坐标预测误差统计直方图

Figure 14. Histogram of Z-axis intercept point's coordinate prediction error

下载: 全尺寸图片幻灯片

图 15 X轴方向拦截点坐标部分样本预测误差

Figure 15. X-axis intercept point's coordinate partial sample prediction error

下载: 全尺寸图片幻灯片

图 16 Y轴方向拦截点坐标部分样本预测误差

Figure 16. Y-axis intercept point's coordinate partial sample prediction error

下载: 全尺寸图片幻灯片

图 17 Z轴方向拦截点坐标部分样本预测误差

Figure 17. Z-axis intercept point's coordinate partial sample prediction error

下载: 全尺寸图片幻灯片

图 18 各方向拦截点坐标预测误差柱状图

Figure 18. Bar chart of error in different directions of intercept point prediction coordinate axis

下载: 全尺寸图片幻灯片

图 19 各方向拦截点坐标预测误差箱型图

Figure 19. Error box plot in different directions of intercept point prediction coordinate axis

下载: 全尺寸图片幻灯片

图 20 神经网络预测结果与弹道仿真结果的比较

Figure 20. Comparison of neural network predictionresults and trajectory simulation results

下载: 全尺寸图片幻灯片

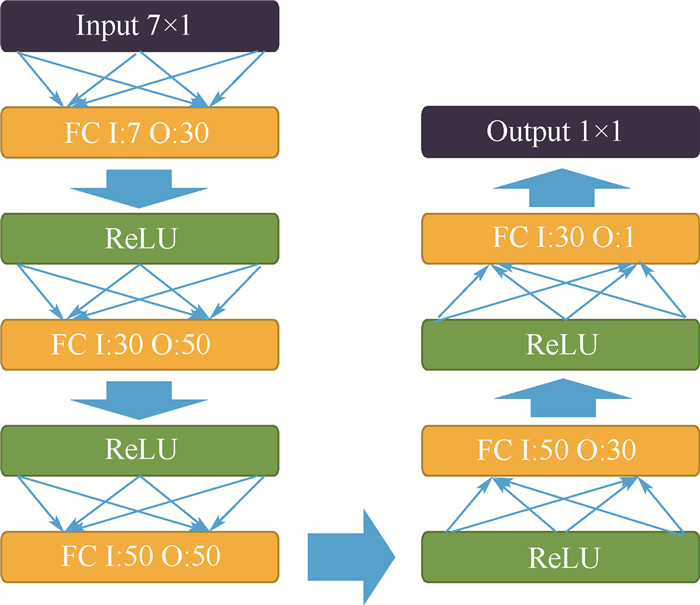
表 1 拦截时间预测网络结构

Table 1. Intercept time prediction network structure

层名称	网络结构
输入层	7
全连接层1	I: 7 O: 30
激活函数1	ReLU
全连接层2	I: 30 O: 50
激活函数2	ReLU
全连接层3	I: 50 O: 50
激活函数3	ReLU
全连接层4	I: 50 O: 30
激活函数4	ReLU
全连接层5	I: 30 O: 1
输出层	1

下载: 导出CSV

表 2 拦截点预测网络结构

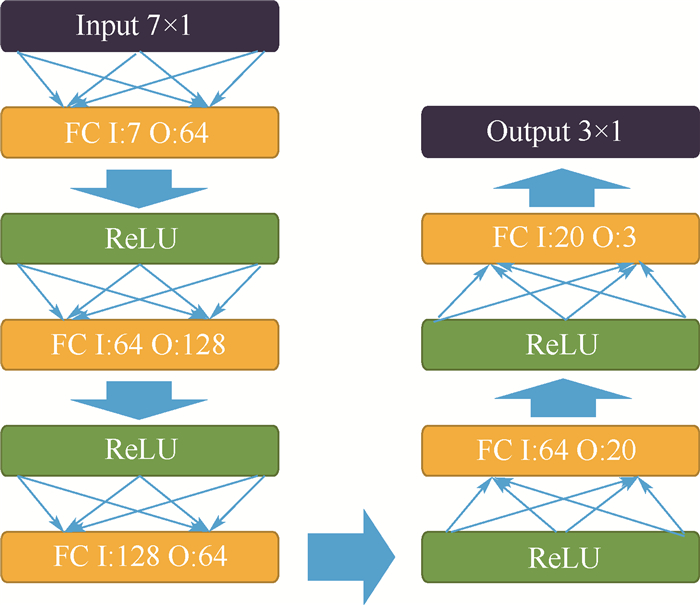
Table 2. Intercept point prediction network structure

层名称	网络结构
输入层	7
全连接层1	I: 7 O: 64
激活函数1	ReLU
全连接层2	I: 64 O: 128
激活函数2	ReLU
全连接层3	I: 128 O: 64
激活函数3	ReLU
全连接层4	I: 64 O: 20
激活函数4	ReLU
全连接层5	I: 20 O: 1
输出层	3

下载: 导出CSV

表 3 预测网络训练参数

Table 3. Prediction network training parameters

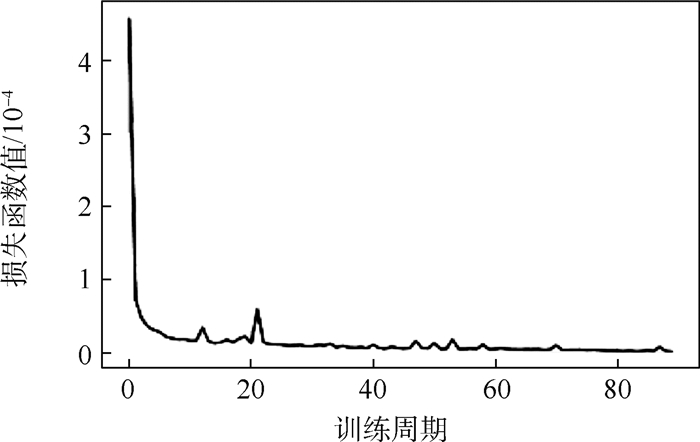
训练参数	拦截时间预测网络	拦截点预测网络
批尺寸	1	100
学习率	0.000 1	0.000 1
训练周期	94	54

下载: 导出CSV

表 4 拦截时间预测误差

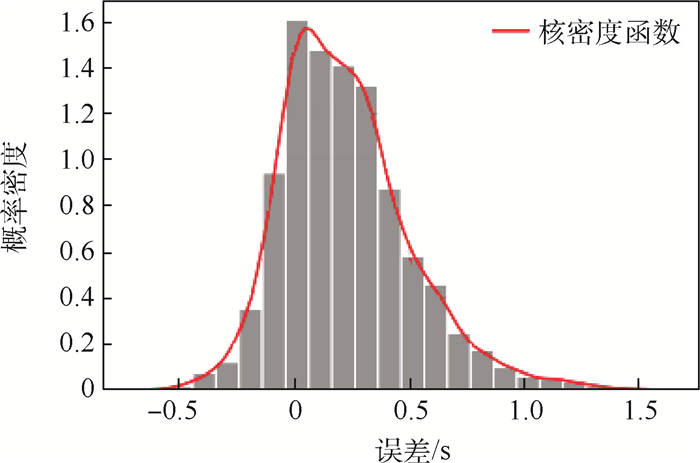
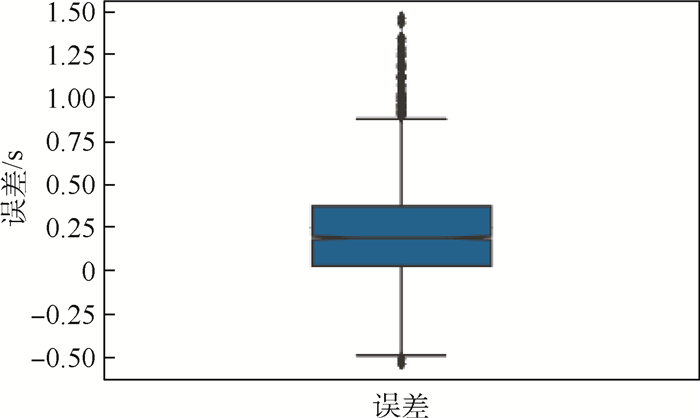
Table 4. Prediction error of intercept time

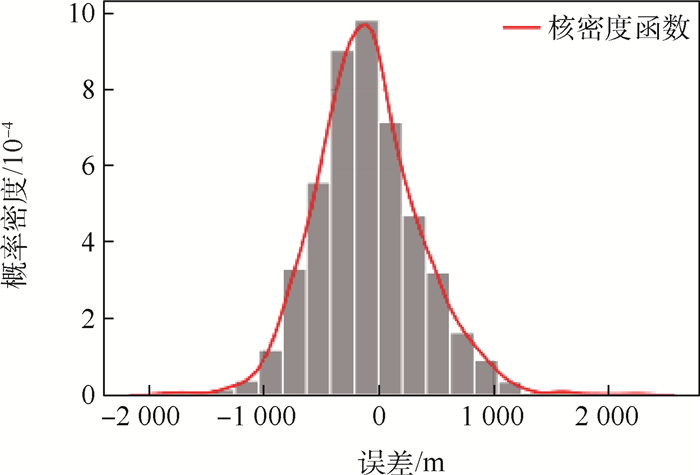
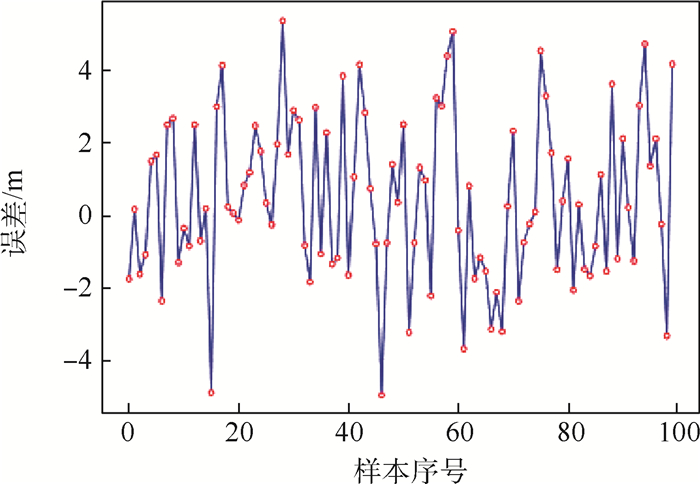
误差类型	平均值/s	最大值(绝对值)	标准差/s
相对误差		0.124 3%
误差	0.224 0	1.467 5 s	0.281 1

下载: 导出CSV

表 5 拦截点坐标预测误差

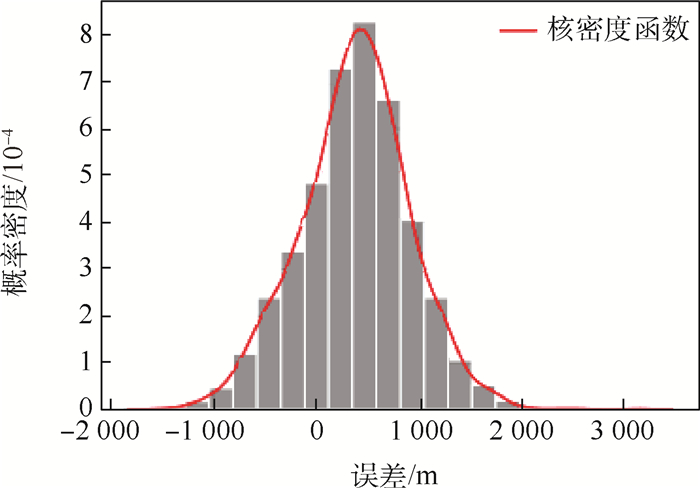
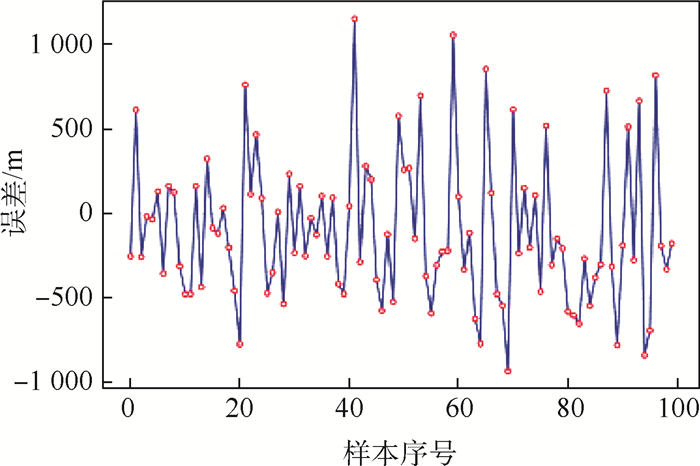
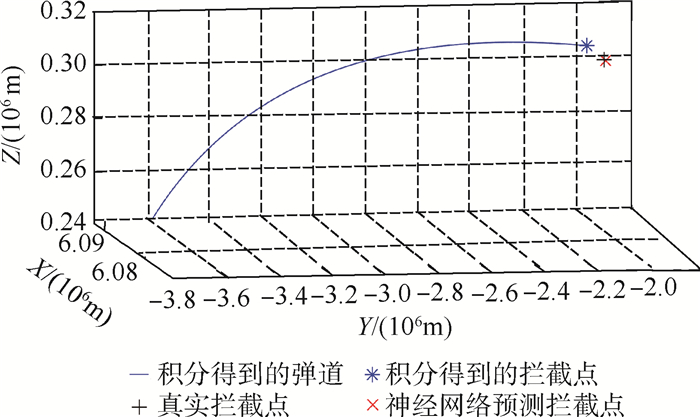
Table 5. Prediction error of intercept point's coordinates

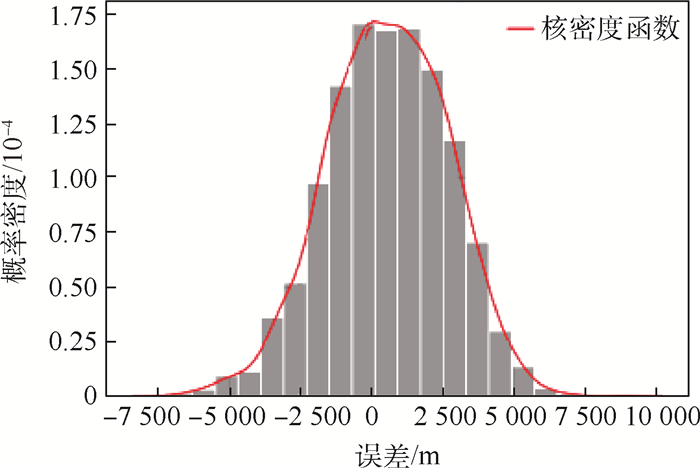
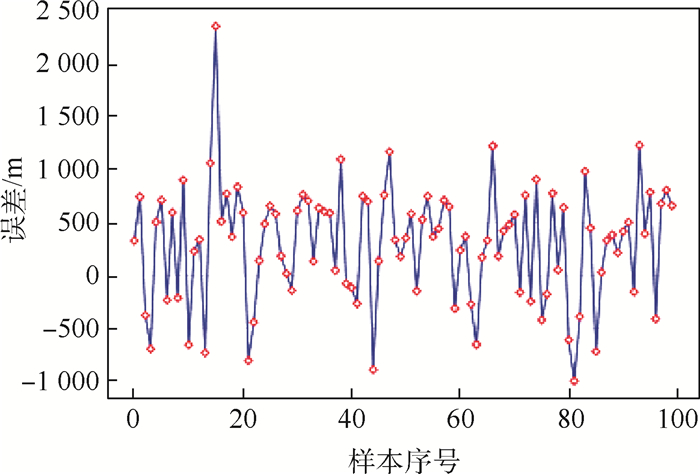
误差类型	平均值	最大值(绝对值)	标准差
相对误差/%		0.128 5
距离误差/m	2 016.48	9 255.64	1 223.14
X轴坐标误差/m	379.45	3 150.91	536.05
Y轴坐标误差/m	552.48	8 928.98	2 146.45
Z轴坐标误差/m	94.60	2 293.46	457.69

下载: 导出CSV

参考文献(20)

[1]	鲜勇, 郑晓龙. 弹道导弹攻防仿真系统建模[M]. 北京: 国防工业出版社, 2013: 14. XIAN Y, ZHENG X L. Modeling of ballistic missile attack and defense simulation system[M]. Beijing: National Defense Industry Press, 2013: 14(in Chinese).
[2]	THOMAS K, IAN W, WES R. Missile defense 2020: Next steps for defending the homeland[R]. Washington, D.C. : Center for Strategic International Studies, 2017.
[3]	王虎, 邓大松. 地基拦截弹发展研究[J]. 战术导弹技术, 2019(3): 34-40. https://www.cnki.com.cn/Article/CJFDTOTAL-ZSDD201903006.htm WANG H, DENG D S. Study on development of ground-based interceptor[J]. Tactical Missile Technology, 2019(3): 34-40(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZSDD201903006.htm
[4]	田宪科, 张科. 导弹拦截点计算及其仿真分析[J]. 飞行力学, 2011, 29(2): 93-97. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201102024.htm TIAN X K, ZHANG K. Calculation and simulation analysis of missile intercept point[J]. Flight Dynamics, 2011, 29(2): 93-97(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201102024.htm
[5]	张华伟, 董茜, 王文灿, 等. 基于预测命中点的反弹道导弹拦截方法研究[J]. 弹箭与制导学报, 2007(2): 196-199. doi: 10.3969/j.issn.1673-9728.2007.02.062 ZHANG H W, DONG Q, WANG W C, et al. Research way of intercepting ballistic missile based on the forecasting hitting position[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007(2): 196-199(in Chinese). doi: 10.3969/j.issn.1673-9728.2007.02.062
[6]	王君, 周林, 雷虎民. 地空导弹与空中目标遭遇点预测模型和算法[J]. 系统仿真学报, 2009, 21(1): 80-83. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200901022.htm WANG J, ZHOU L, LEI H M. Forecast model and arithmetic on hit point of ground-to-air missile and aerial target[J]. Journal of System Simulation, 2009, 21(1): 80-83(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200901022.htm
[7]	ZARCHAN P. Tactical and strategic missile guidance[M]. 6th ed. Reston: AIAA, 2012: 213-324, 715-862.
[8]	谢经纬, 陈万春. 大气层外拦截弹建模与攻防效能分析[J]. 北京航空航天大学学报, 2018, 44(9): 1826-1838. doi: 10.13700/j.bh.1001-5965.2018.0095 XIE J W, CHEN W C. Exo-atmospheric interceptor modeling and penetration and defense effectiveness analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(9): 1826-1838(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0095
[9]	SONG E J, TAHK M J. Three-dimensional midcourse guidance using neural networks for interception of ballistic targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 404-414. doi: 10.1109/TAES.2002.1008975
[10]	SONG E J, LEE H, TAHK M. On-line suboptimal midcourse guidance using neural networks[C]//Proceedings of the 35th SICE Annual Conference International Session Papers. Piscataway: IEEE Press, 1996: 1313-1318.
[11]	SONG E J, TAHK M J. Real-time midcourse guidance with intercept point prediction[J]. Control Engineering Practice, 1998, 6(8): 957-967. doi: 10.1016/S0967-0661(98)00041-0
[12]	袁亚军. 中远程导弹防御指控系统设计与仿真评估研究[D]. 哈尔滨: 哈尔滨工业大学, 2017: 11-13. YUAN Y J. The designation and research on middle-long range missile defense system command and control[D]. Harbin: Harbin Institute of Technology, 2017: 11-13(in Chinese).
[13]	CHIA H, TAN C, SUNG S. Enhancing knowledge discovery via association-based evolution of neural logic networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(7): 889-901. doi: 10.1109/TKDE.2006.111
[14]	XU J X, HOU Z S. Notes on data-driven system approaches[J]. Acta Automatica Sinica, 2009, 35(6): 668-675. http://aas.net.cn/CN/article/downloadArticleFile.do?attachType=PDF&id=13329
[15]	CHEN S, BILLINGS S A. Neural networks for nonlinear dynamic system modelling and identification[J]. International Journal of Control, 1991, 56(2): 319-346. http://www.onacademic.com/detail/journal_1000035255651810_b8c0.html
[16]	LESHNO M, LIN V Y, PINKUS A, et al. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function[J]. Neural Networks, 1991, 6(6): 861-867. http://archive.nyu.edu/bitstream/2451/14384/1/IS-91-26.pdf
[17]	GOLIK P, DOETSCH P, NEY H. Cross-entropy vs. squared error training: A theoretical and experimental comparison[C]//Interspeech, 2013: 1756-1760.
[18]	ALMÁSI A, WOZ'NIAK S, CRISTEA V, et al. Review of advances in neural networks: Neural design technology stack[J]. Neurocomputing, 2016, 174: 31-41. http://cld.pt/dl/download/5cf0dc5f-72b0-4b05-953e-484f624b49f6/MyPapers/l984jnf_5506.pdf
[19]	GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge: MIT Press, 2016.
[20]	刘孝马. 大气层外动能拦截器中段制导相关问题研究[D]. 长沙: 国防科学技术大学, 2015: 13. LIU X M. Research on the problems about midcourse guidance for exo-atmospheric kill vehicle[D]. Changsha: National University of Defense Technology, 2015: 13(in Chinese).