基于可靠性的CFRP螺栓连接优化设计方法

山美娟; 赵丽滨

doi:10.13700/j.bh.1001-5965.2020.0425

基于可靠性的CFRP螺栓连接优化设计方法

doi: 10.13700/j.bh.1001-5965.2020.0425

山美娟¹,
赵丽滨^2, ,

1.
北京交通大学土木建筑工程学院, 北京 100044
2.
北京航空航天大学宇航学院, 北京 100083

基金项目:

国家自然科学基金 11772028

中国博士后科学基金 2020M680325

详细信息

通讯作者:
赵丽滨, E-mail: lbzhao@buaa.edu.cn

中图分类号: TB330.1;V214.8
计量
- 文章访问数: 595
- HTML全文浏览量: 117
- PDF下载量: 102
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-12
- 录用日期: 2020-11-20
- 网络出版日期: 2021-11-20

Reliability-based design optimization method of CFRP bolted joints

SHAN Meijuan¹,
ZHAO Libin^{2
, ,}

1.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
2.
School of Astronautics, Beihang University, Beijing 100083, China

Funds:

National Natural Science Foundation of China 11772028

China Postdoctoral Science Foundation 2020M680325

More Information

Corresponding author: ZHAO Libin, E-mail: lbzhao@buaa.edu.cn

摘要

摘要:
螺栓连接是复合材料结构的薄弱环节。因此，螺栓连接部位的设计是先进复合材料结构设计的关键之一。将修正特征曲线方法和随机参数统计模型结合，建立了碳纤维增强复合材料（CFRP）螺栓连接失效载荷的概率分析模型，进而以关键影响参数为设计变量，以可靠度指标为约束，以连接结构质量为设计目标，发展了基于可靠性的CFRP螺栓连接优化设计方法。采用正交试验设计方法建立基于可靠性的螺栓连接优化设计计算方案，优化结果表明：关键影响参数X_C为2 450 MPa、t_ply为0.174 mm、E₁₁为225 GPa时的设计方案为螺栓连接最佳设计方案，该方案使得外载荷为17.5 kN时，螺栓连接可靠度由0.998提高到0.999 999以上，同时使得连接结构的质量下降了6.44%。
- 复合材料螺栓连接 /
- 失效载荷 /
- 可靠度指标 /
- 基于可靠性的优化设计 /
- 特征曲线方法
Abstract:
Bolted joints are the weak points of composite structures. Therefore, the design of bolted joints is one of crucial issues in the design of composite structure. In this paper, a probability analysis model for the failure load of a Carbon Fiber Reinforced Polymer (CFRP) composite bolted joint was built by combining the modified characteristic curve method and the statistical model of random parameters. The key influence parameters were regarded as the design variables, the reliability index was considered as the constraint, and the mass of the joint was the design goal. Accordingly, a reliability-based design optimization method was developed for the CFRP bolted joint. The orthogonal test design method was used to establish the reliability-based optimal design calculation scheme. The optimization results show that, when the key influence parameters X_C is 2 450 MPa, t_ply is 0.174 mm, and E₁₁ is 225 GPa, the best design of the joint is obtained. According to this scheme, when the external load is 17.5 kN, the reliability of the joint is increased from 0.998 to above 0.999 999, and the mass of the joint is reduced by 6.44%.
- composite bolted joints /
- failure load /
- reliability index /
- reliability-based design optimization /
- characteristic curve method

HTML全文

图 1 CFRP单钉双剪连接结构示意图

Figure 1. Schematic diagram of CFRP single-bolt double-lap joint structure

下载: 全尺寸图片幻灯片

图 2 修正的特征曲线示意图

Figure 2. Schematic diagram of modified characteristic curve

下载: 全尺寸图片幻灯片

图 3 螺栓连接的有限元模型

Figure 3. Finite element model of bolted joint

下载: 全尺寸图片幻灯片

图 4 基于可靠性的螺栓连接优化设计过程

Figure 4. Reliability-based design optimization process of bolted joint

下载: 全尺寸图片幻灯片

表 1 CFRP层压板几何尺寸和铺层角度的名义值

Table 1. Nominal geometrical dimensions and fiber orientation angles of CFRP laminate

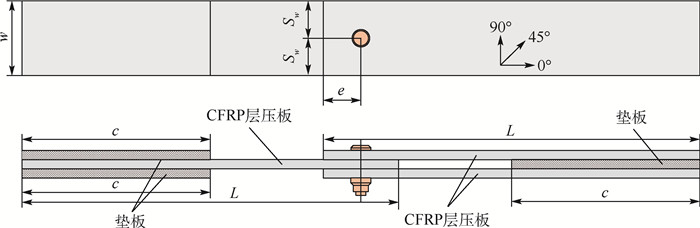
几何尺寸	w/mm	S_w/mm	e/mm	D/mm	t_ply/mm
数值	30	15	15	4.76	0.185

纤维铺设角度	θ₁/(°)	θ₂/(°)	θ₃/(°)	θ₄/(°)
数值	0	90	45	-45

下载: 导出CSV

表 2 复合材料基本力学性能的平均值

Table 2. Means of basic mechanical properties of composites

弹性参数	E₁₁/GPa		E₂₂/GPa	G₁₂/GPa	υ₁₂
数值	195		8.58	4.57	0.33

强度参数	X_T/MPa	X_C/MPa	Y_T/MPa	Y_C/MPa	S₁₂/MPa
数值	3 071	1 747	88	271	143

下载: 导出CSV

表 3 螺栓连接随机参数的统计模型

Table 3. Statistical model of random parameters of bolted joint

类型	随机变量	期望值μ	标准差σ	分布类型
几何尺寸	w/mm	30	0.333	正态
	S_w/mm	15	0.167	正态
	e/mm	15	0.333	正态
	D/mm	4.76	0.01	正态
	t_ply/mm	设计变量		正态
纤维铺设角度	θ₁/(°)	0	0.9	正态
	θ₂/(°)	90	0.9	正态
	θ₃/(°)	45	0.9	正态
	θ₄/(°)	-45	0.9	正态
材料性能	E₁₁/GPa	设计变量		正态
	E₂₂/GPa	8.58	0.086	正态
	G₁₂/GPa	4.57	0.098	正态
	υ₁₂	0.33	0.020	正态
	X_T/MPa	3 071	187.4	正态
	X_C/MPa	设计变量		正态
	Y_T/MPa	88	7.7	正态
	Y_C/MPa	271	22.4	正态
	S₁₂/MPa	143	3.9	正态

下载: 导出CSV

表 4 设计变量的取值

Table 4. Values of design variables

设计变量	初始值			水平1	水平2	水平3
设计变量	μ	σ	COV	μ₁=μ-nσ	μ₂=μ	μ₃=μ+nσ
X_C	1 750 MPa	66.5 MPa	0.038	1 050 MPa	1 750 MPa	2 450 MPa
t_ply	0.186 mm	0.004 mm	0.022	0.174 mm	0.186 mm	0.198 mm
E₁₁	195 GPa	3.8 GPa	0.02	165 GPa	195 GPa	225 GPa

下载: 导出CSV

表 5 基于正交试验设计的计算方案及目标函数值

Table 5. Calculation scheme based on orthogonal experimental design and objective function value

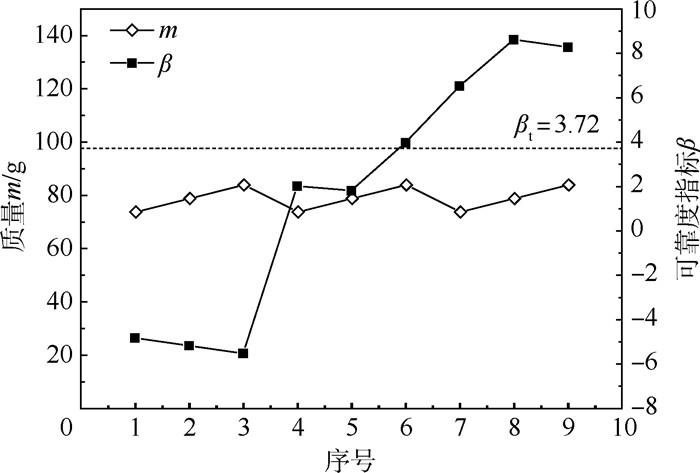
方案序号	X_C/MPa	t_ply/mm	E₁₁/GPa	β	m/g
1	1 050	0.174	165	-4.82	73.75
2	1 050	0.186	195	-5.17	78.83
3	1 050	0.198	225	-5.52	83.92
4	1 750	0.174	195	2.02	73.75
5	1 750	0.186	225	1.82	78.83
6	1 750	0.198	165	3.98	83.92
7	2 450	0.174	225	6.52	73.75
8	2 450	0.186	165	8.62	78.83
9	2 450	0.198	195	8.28	83.92

下载: 导出CSV

参考文献(27)

[1]	MCCARTHY M A. BOJCAS: Bolted joints in composite aircraft structures[J]. Air & Space Europe, 2001, 3(3/4): 139-142. http://www.sciencedirect.com/science/article/pii/S1290095801900772
[2]	MANGALGIRI P D. Design allowable considerations for use of laminated composites in aircraft structures[J]. Journal of the Indian Institute of Science, 2013, 93(4): 571-592. http://journal.iisc.ernet.in/index.php/iisc/article/view/4327/0
[3]	ATAS A, SOUTIS C. Damage and failure analysis of bolted joints in composite laminates[M]//BEAUMONT P W R, SOUTIS C, HODZIC A. The structural integrity of carbon fiber composites. Berlin: Springer, 2017: 591-644.
[4]	赵丽滨, 刘丰睿, 黄伟, 等. 复合材料螺栓连接失效分析研究进展[J]. 强度与环境, 2017, 44(3): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHJ201703001.htm ZHAO L B, LIU F R, HUANG W, et al. Advances in failure analysis methods of bolted composite joints[J]. Structure & Environment Engineering, 2017, 44(3): 1-11(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QDHJ201703001.htm
[5]	SOARES C G. Reliability of components in composite materials[J]. Reliability Engineering and System Safety, 1997, 55(2): 171-177. doi: 10.1016/S0951-8320(96)00008-7
[6]	CHIACHIO M, CHIACHIO J, RUS G. Reliability in composites-A selective review and survey of current development[J]. Composites Part B: Engineering, 2012, 43(3): 902-913. doi: 10.1016/j.compositesb.2011.10.007
[7]	王佩艳, 朱振涛, 王富生, 等. 复合材料螺栓连接性能的分散性和可靠性分析[J]. 力学季刊, 2008, 29(4): 573-577. https://www.cnki.com.cn/Article/CJFDTOTAL-SHLX200804010.htm WANG P Y, ZHU Z T, WANG F S, et al. Dispersibility and reliability analysis of composite laminates bolted joint[J]. Chinese Quarterly of Mechanics, 2008, 29(4): 573-577(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SHLX200804010.htm
[8]	KHASHABA U A, SEBAEY T A, ALNEFAIE K A. Failure and reliability analysis of pinned-joint composite laminates: Effects of pin-hole clearance[J]. Journal of Composite Materials, 2013, 47(18): 2287-2298. doi: 10.1177/0021998312457196
[9]	KHASHABA U A, SEBAEY T A, ALNEFAIE K A. Failure and reliability analysis of pinned-joints composite laminates: Effects of stacking sequences[J]. Composites Part B: Engineering, 2013, 45(1): 1694-1703. doi: 10.1016/j.compositesb.2012.09.066
[10]	LI H S, LU Z Z, ZHANG Y. Probabilistic strength analysis of bolted joints in laminated composites using point estimate method[J]. Composite Structures, 2009, 88(2): 202-211. doi: 10.1016/j.compstruct.2008.03.040
[11]	LI H S. Maximum entropy method for probabilistic failure load prediction of pin joints in composite laminates[J]. Composite Structures, 2013, 106: 626-634. doi: 10.1016/j.compstruct.2013.05.040
[12]	LI H S, XIA S, LUO D M. A probabilistic analysis for pin joint failure load in composite laminates using subset simulation[J]. Composites Part B: Engineering, 2014, 56: 780-789. doi: 10.1016/j.compositesb.2013.09.025
[13]	NAKAYAMA M, UDA N, ONO K. Probabilistic assessment of pin joint strength in CFRP laminates[J]. Composite Structures, 2011, 93(8): 2026-2030. doi: 10.1016/j.compstruct.2011.02.019
[14]	NAKAYAMA M, UDA N, ONO K, et al. Design-oriented strength of mechanical joints in composite laminate structures and reliability-based design factor[J]. Composite Structures, 2015, 132: 1-11. doi: 10.1016/j.compstruct.2015.04.044
[15]	左健巍. 复合材料结构的重要性测度[C]//第四届中国航空科学技术大会, 2019: 264-277. ZUO J W. Importance measure on composite material structures[C]//Proceedings of the 4th China Aviation Science and Technology Conference, 2019: 264-277(in Chinese).
[16]	高魁垠, 李海波, 吴建国, 等. 2D-C/SiC复合材料螺栓连接结构可靠性分析[J]. 强度与环境, 2020, 47(1): 33-40. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHJ202001005.htm GAO K Y, LI H B, WU J G, et al. Reliability analysis of 2D-C/SiC composite bolted joints[J]. Structure & Environment Engineering, 2020, 47(1): 33-40(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QDHJ202001005.htm
[17]	ZHAO L, SHAN M, LIU F, et al. A probabilistic model for strength analysis of composite double-lap single-bolt joints[J]. Composite Structures, 2017, 161: 419-427. doi: 10.1016/j.compstruct.2016.11.074
[18]	LIU F, FANG Z, ZHAO L, et al. A failure-envelope-based method for the probabilistic failure prediction of composite multi-bolt double-lap joints[J]. Composites Part B: Engineering, 2019, 172: 593-602. doi: 10.1016/j.compositesb.2019.05.034
[19]	YANG L, MA Z. Optimum design based on reliability for a composite structural system[J]. Computers & Structures, 1990, 36(5): 785-790. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-004579499090148U&originContentFamily=serial&_origin=article&_ts=1433603102&md5=1b48ed21276492e08a4afbfc8cfaa98a
[20]	MUROTSU Y, MIKI M, SHAO S. Reliability design of fiber reinforced composites[J]. Structural Safety, 1994, 15(1-2): 35-49. doi: 10.1016/0167-4730(94)90051-5
[21]	CHANG F K, SCOTT R A, SPRINGER G S. Strength of mechanically fastened composite joints[J]. Journal of Composite Materials, 1982, 16(6): 470-494. doi: 10.1177/002199838201600603
[22]	XIONG Y. An analytical method for failure prediction of multi-fastener composite joints[J]. International Journal of Solids and Structures, 1996, 33(29): 4395-4409. doi: 10.1016/0020-7683(95)00231-6
[23]	ZHANG J M. Design and analysis of mechanically fastened composite joints and repairs[J]. Engineering Analysis with Boundary Elements, 2001, 25(6): 431-441. doi: 10.1016/S0955-7997(01)00049-2
[24]	ZHANG J, LIU F, ZHAO L, et al. A novel characteristic curve for failure prediction of multi-bolt composite joints[J]. Composite Structures, 2014, 108: 129-136. doi: 10.1016/j.compstruct.2013.09.019
[25]	CHOI S K, GRANDHI R V, CANFIELD R A. 结构可靠性设计[M]. 芮强, 王红岩, 译. 北京: 国防工业出版社, 2014. CHOI S K, GRANDHI R V, CANFIELD R A. Reliability-based structural design[M]. RUI Q, WANG H Y, translated. Beijing: National Defense Industry Press, 2014(in Chinese).
[26]	ZHANG J, LIU F, ZHAO L, et al. Investigation on characteristic length testing methods for failure prediction of composite multi-bolt joints[J]. Journal of Reinforced Plastics and Composites, 2015, 34(8): 636-648. doi: 10.1177/0731684415574871
[27]	YAMADA S E, SUN C T. Analysis of laminate strength and its distribution[J]. Journal of Composite Materials, 1978, 12: 275-284. doi: 10.1177/002199837801200305