长周期高精度回归轨道与脉冲轨道控制策略设计

何艳超; 徐明

doi:10.13700/j.bh.1001-5965.2021.0178

长周期高精度回归轨道与脉冲轨道控制策略设计

doi: 10.13700/j.bh.1001-5965.2021.0178

何艳超^1, ,,
徐明²

1.
航天东方红卫星有限公司, 北京 100094
2.
北京航空航天大学宇航学院, 北京 100083

基金项目:

中国航天科技集团有限公司钱学森青年创新基金

详细信息

通讯作者:
何艳超, E-mail: heyanchao@buaa.edu.cn

中图分类号: V412.4⁺1
计量
- 文章访问数: 615
- HTML全文浏览量: 95
- PDF下载量: 114
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-07
- 录用日期: 2021-04-23
- 网络出版日期: 2021-11-20

Design of long-duration high-precision repeat ground-track orbit and its impulsive orbital control strategy

HE Yanchao^{1
, ,},
XU Ming²

1.
DFH Satellite Co., Ltd., Beijing 100094, China
2.
School of Astronautics, Beihang University, Beijing 100083, China

Funds:

Qian Xuesen Youth Innovation Foundation of China Aerospace Science and Technology Corporation

More Information

Corresponding author: HE Yanchao, E-mail: heyanchao@buaa.edu.cn

摘要

摘要:
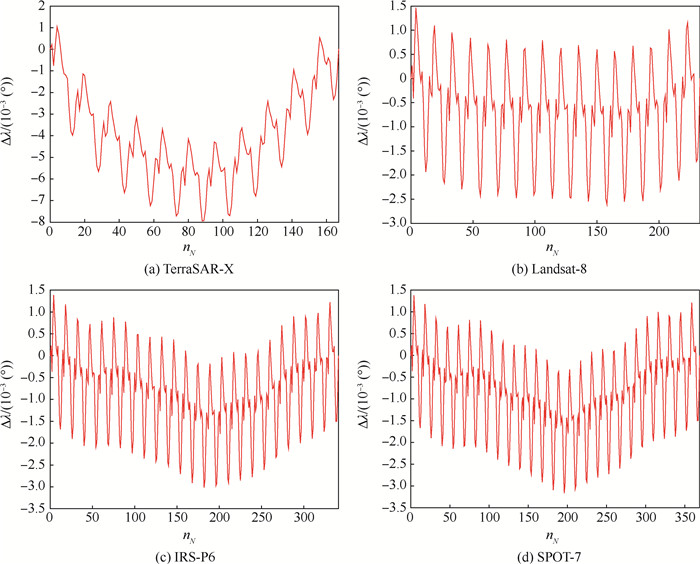
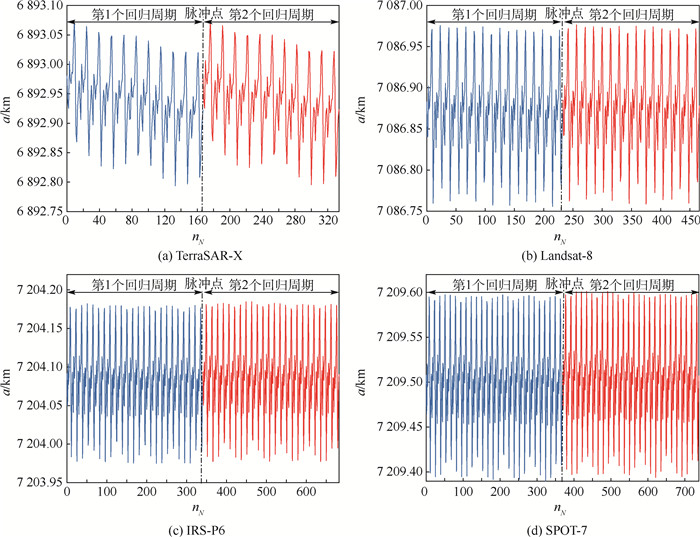
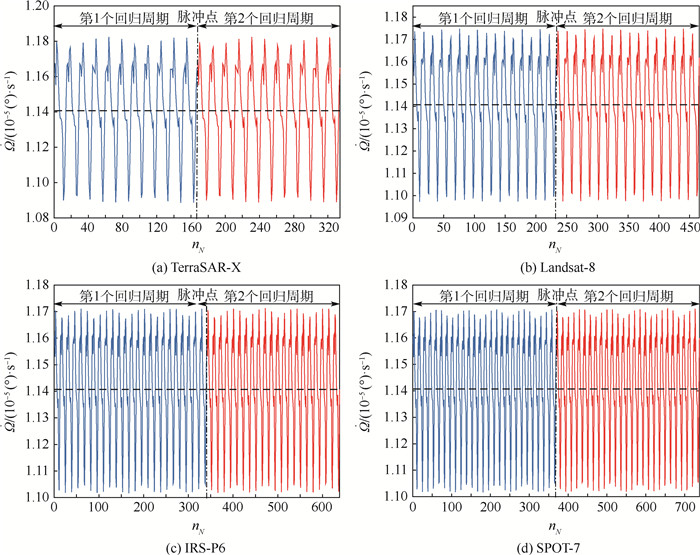
针对长周期回归轨道设计和维持问题，研究了一种基于高阶Poincaré映射的高精度引力场中回归轨道优化设计和控制的通用性半解析方法，其中摄动包含大气阻力、太阳辐射压力和日月三体引力等因素。通过对Poincaré映射进行高阶展开并表示为多项式形式，可精确近似对一个或者多个回归周期内的轨道递推，从而在赤道升交点处施加脉冲推力，实现高精度的回归轨道设计和控制。提出了分别解决严格和宽松2种回归约束下问题的方法，并应用于实际在轨TerraSAR-X、Landsat-8、IRS-P6、SPOT-7和UoSAT-12任务的回归模式。所提方法具有计算效率和精度高的优点，可用于星上自主轨道递推和轨道控制。
- 回归轨道 /
- 高阶Poincaré映射 /
- 半解析设计 /
- 严格回归约束 /
- 宽松回归约束
Abstract:
Aimed at the design and maintenance of long-duration repeat ground-track orbit, this paper deals with a semi-analytical method based on high-order Poincaré maps for the optimal design and control of repeat ground-track orbit in the high-precision gravity fields, including the factors of atmospheric drag, solar radiation pressure and three-body perturbations. The method is based on the high-order expansion of Poincaré maps, which is expressed as the polynomials, to propagate the orbit for one or more repeat cycles, enabling the precise orbit design and control by performing impulsive control at the equatorial crossings. The method, aimed at both the high-accuracy and low-accuracy constraints, is proposed and applied to missions like the repeat pattern of TerraSAR-X, Landsat-8, IRS-P6, SPOT-7 and UoSAT-12. The present method has the advantages in high computational efficiency and high accuracy, which is suitable for the on-board autonomous orbital propagation and orbital control.
- repeat ground-track orbit /
- high-order Poincaré maps /
- semi-analytical design /
- high-accuracy constraint /
- low-accuracy constraint

HTML全文

图 1 地心惯性坐标系和地心固连坐标系

Figure 1. Earth-centered inertial and Earth-centered, Earth-fixed coordinate frames

下载: 全尺寸图片幻灯片

图 2 x₀邻域内初始点(x₀+δx₀)在t_f处的近似解

Figure 2. Approximation of initial value (x₀+δx₀) in the neighborhood of x₀ at t_f

下载: 全尺寸图片幻灯片

图 3 升交点处经度实际值与标称值的对比

Figure 3. Comparison of actual and nominal longitude values at ascending nodes

下载: 全尺寸图片幻灯片

图 4 一个回归周期内每圈轨道升交点处经度实际值与其标称值对比的漂移量

Figure 4. Drift value of actual longitude compared with nominal one at ascending nodes of each cycle of orbit during one repeat cycle

下载: 全尺寸图片幻灯片

图 5 施加脉冲机动前后半长轴的演化

Figure 5. Evolution of semi-major axis before and after impulsive maneuvers

下载: 全尺寸图片幻灯片

图 6 施加脉冲机动前后轨道倾角的演化

Figure 6. Evolution of inclination before and after impulsive maneuvers

下载: 全尺寸图片幻灯片

图 7 施加脉冲机动前后升交点赤经漂移率的演化

Figure 7. Evolution of drift rate of right ascension of ascending node before and after impulsive maneuvers

下载: 全尺寸图片幻灯片

图 8 基于微分代数方法和轨道递推方法的经度对比结果

Figure 8. Comparison of longitude values obtained by DA-based orbital propagation and numerical integration-based orbital propagation

下载: 全尺寸图片幻灯片

图 9 三个回归周期内经度的实际值与标称值对比

Figure 9. Comparison of actual and nominal longitude values during three repeat cycles

下载: 全尺寸图片幻灯片

图 10 轨道控制后轨迹经度与其初始值的偏差

Figure 10. Deviation of actual orbital longitude from initial longitude after orbital control

下载: 全尺寸图片幻灯片

图 11 六个回归周期内半长轴和轨道倾角的演化

Figure 11. Evolution of semi-major axis and inclination within six repeat cycles

下载: 全尺寸图片幻灯片

表 1 TerraSAR-X回归模式算例轨道控制结果

Table 1. Orbital control results of TerraSAR-X repeat pattern

状态量	第1个回归周期		第2个回归周期
状态量	初始	终止	初始	终止
x/km	6 784.509 118	6 784.508 908	6 784.508 908	6 784.508 491
y/km	-1 198.825 274	-1 198.825 404	-1 198.825 404	-1 198.825 332
z/km	0	0	0	0
v_x/(km·s^-1)	-0.268 267 730	-0.268 211 934	-0.268 272 691	-0.268 244 003
v_y/(km·s^-1)	-1.463 279 438	-1.463 277 386	-1.463 278 583	-1.463 459 538
v_z/(km·s^-1)	7.544 055 446	7.544 025 069	7.544 055 978	7.544 001 930
T/s	950 399.38		950 399.64

下载: 导出CSV

表 2 Landsat-8回归模式算例轨道控制结果

Table 2. Orbital control results of Landsat-8 repeat pattern

状态量	第1个回归周期		第2个回归周期
状态量	初始	终止	初始	终止
x/km	6 975.552 101	6 975.551 558	6 975.551 558	6 975.551 381
y/km	-1 232.582 639	-1 232.582 799	-1 232.582 799	-1 232.582 778
z/km	0	0	0	0
v_x/(km·s^-1)	-0.285 046 636	-0.285 007 355	-0.285 073 308	-0.285 030 544
v_y/(km·s^-1)	-1.561 515 791	-1.561 706 363	-1.561 705 676	-1.561 855 639
v_z/(km·s^-1)	7.426 314 342	7.426 284 548	7.426 288 429	7.426 264 784
T/s	1 382 399		1 382 399.6

下载: 导出CSV

表 3 IRS-P6回归模式算例轨道控制结果

Table 3. Orbital control results of IRS-P6 repeat pattern

状态量	第1个回归周期		第2个回归周期
状态量	初始	终止	初始	终止
x/km	7 091.011 029	7 091.010 546	7 091.010 546	7 091.010 247
y/km	-1 252.984 275	-1 252.984 999	-1 252.984 999	-1 252.984 943
z/km	0	0	0	0
v_x/(km·s^-1)	-0.295 622 153	-0.295 550 878	-0.295 647 647	-0.295 609 033
v_y/(km·s^-1)	-1.623 266 169	-1.623 412 825	-1.623 403 153	-1.623 752 336
v_z/(km·s^-1)	7.356 222 412	7.356 200 355	7.356 202 783	7.356 149 740
T/s	2 073 599.4		2 073 600.5

下载: 导出CSV

表 4 SPOT-7回归模式算例轨道控制结果

Table 4. Orbital control results of SPOT-7 repeat pattern

状态量	第1个回归周期		第2个回归周期
状态量	初始	终止	初始	终止
x/km	7 096.348 844	7 096.348 569	7 096.348 569	7 096.348 374
y/km	-1 253.927 469	-1 253.928 444	-1 253.928 444	-1 253.928 404
z/km	0	0	0	0
v_x/(km·s^-1)	-0.296 089 274	-0.296 009 0	-0.296 111 439	-0.296 062 414
v_y/(km·s^-1)	-1.625 981 449	-1.626 113 0	-1.626 098 844	-1.626 408 561
v_z/(km·s^-1)	7.353 025 818	7.353 006 575	7.353 009 099	7.352 962 120
T/s	2 246 398.4		2 246 399.8

下载: 导出CSV

表 5 宽松精度情形下轨道控制结果

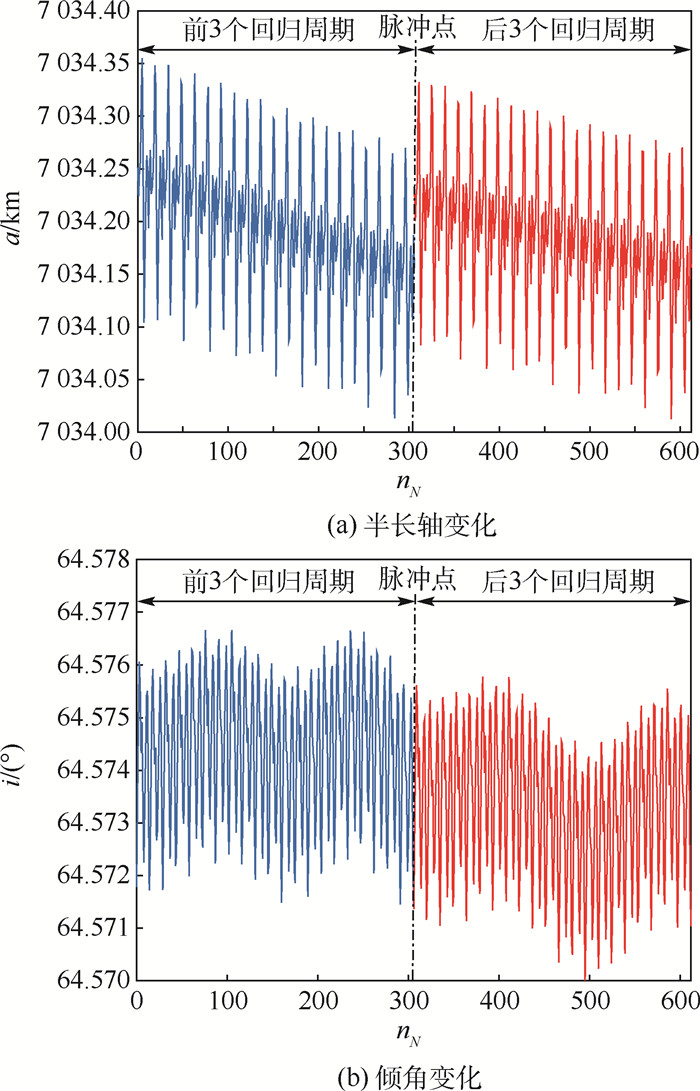
Table 5. Orbital control results for loose-accuracy scenario

状态量	前3个回归周期		后3个回归周期
状态量	初始	终止	初始	终止
x/km	-1 684.591 611	-1 684.515 457	-1 684.515 457	-1 682.767 179
y/km	-6 825.069 865	-6 825.112 359	-6 825.112 359	-6 825.595 939
z/km	0	0	0	0
v_x/(km·s^-1)	2.638 596 174	2.638 601 972	2.638 618 204	2.638 975 345
v_y/(km·s^-1)	-0.666 368 889	-0.666 251 883	-0.666 255 966	-0.665 570 472
v_z/(km·s^-1)	6.802 699 118	6.802 626 184	6.802 660 947	6.802 471 580
t/s	1 794 301.5		1 794 297.6

下载: 导出CSV

参考文献(15)

[1]	LARA M. Searching for repeating ground track orbits: A systematic approach[J]. Journal of the Astronautical Sciences, 1999, 47(3): 177-188. doi: 10.1007/BF03546198?utm_medium=affiliate&utm_content=meta&utm_campaign=DDCN_1_GL01_metadata
[2]	AORPIMAI M, PALMER P L. Repeat-ground track orbit acquisition and maintenance for earth-observation satellites[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 654-659. doi: 10.2514/1.23413
[3]	NADOUSHAN M J, ASSADIAN N. Repeat ground track orbit design with desired revisit time and optimal tilt[J]. Aerospace Science and Technology, 2015, 40: 200-208. doi: 10.1016/j.ast.2014.11.007
[4]	FU X, WU M, TANG Y. Design and maintenance of low-earth repeat-ground-track successive-coverage orbits[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 686-691. doi: 10.2514/1.54780
[5]	LARA M. Repeat ground track orbits of the Earth tesseral problem as bifurcations of the equatorial family of periodic orbits[J]. Celestial Mechanics and Dynamical Astronomy, 2003, 86(2): 143-162. doi: 10.1023/A:1024195900757
[6]	LARA M, RUSSELL R P. Fast design of repeat ground track orbits in high-fidelity geopotentials[J]. Journal of the Astronautical Sciences, 2008, 56(3): 311-324. doi: 10.1007/BF03256555
[7]	杨盛庆, 杜耀珂, 陈筠力. 基于迭代修正方法的严格回归轨道设计[J]. 宇航学报, 2016, 37(4): 420-426. doi: 10.3873/j.issn.1000-1328.2016.04.007 YANG S Q, DU Y K, CHEN J L. Design of strictly-regressive orbit based on iterative adjustment method[J]. Journal of Astronautics, 2016, 37(4): 420-426(in Chinese). doi: 10.3873/j.issn.1000-1328.2016.04.007
[8]	SENGUPTA P, VADALI S R, ALFRIEND K T. Satellite orbit design and maintenance for terrestrial coverage[J]. Journal of Spacecraft and Rockets, 2010, 47(1): 177-187. doi: 10.2514/1.44120
[9]	温生林, 闫野, 张华. 低轨回归轨道卫星轨迹漂移特性分析与控制[J]. 系统工程与电子技术, 2015, 37(3): 613-619. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201503023.htm WEN S L, YAN Y, ZHANG H. Analysis and control of groundtrack drift for recursive low Earth orbit satellites[J]. Systems Engineering and Electronic, 2015, 37(3): 613-619(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201503023.htm
[10]	张冲难, 卞燕山, 王西京, 等. 严格回归轨道自动生成算法及实现[J]. 推进技术, 2018, 39(7): 1472-1478. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201807004.htm ZHANG C N, BIAN Y S, WANG X J, et al. Algorithm and implementation of automatic generation of rigorous recursive orbit[J]. Journal of Propulsion Technology, 2018, 39(7): 1472-1478(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201807004.htm
[11]	BERZ M. Modern map methods in particle beam physics[M]. London: Academic Press, 1999.
[12]	BERZ M, MAKINO K. COSY INFINITY version 8.1 user's guide and reference manual[Z]. East Lansing: Michigan State University, 2002.
[13]	HE Y, ARMELLIN R, XU M. Bounded relative orbits in the zonal problem via high-order Poincaré maps[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(1): 91-108. doi: 10.2514/1.G003612
[14]	杨盛庆, 杜耀珂, 王文妍, 等. 严格回归轨道的管道导航方法研究[J]. 中国空间科学技术, 2017, 37(6): 10-16. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKJ201706003.htm YANG S Q, DU Y K, WANG W Y, et al. Study on the tube navigation of strictly regressive orbit[J]. Chinese Space Science and Technology, 2017, 37(6): 10-16(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKJ201706003.htm
[15]	FOUQUET M, SWEETING M. UoSAT-12 minisatellite for high performance Earth observation at low cost[J]. Acta Astronautica, 1997, 41(3): 173-182. doi: 10.1016/S0094-5765(97)00181-1